基于折衷規劃法的多工況結構拓撲優化設計

葉增沈 王凡超 鄭 凱 吳劍國

（1.浙江工業大學 土木工程學院 杭州 310023；2.中國船舶及海洋工程設計研究院 上海 200011）

0 引 言

結構優化設計指的是總體的、目標明確的過程和方法，綜合考慮多方面的約束條件，通常以最少的材料、最低的造價或最簡單的工序為目標，尋求結構最佳的布設拓撲亦或是形狀亦或是尺寸。隨著結構優化技術的迅速發展，許多有限元軟件（如HyperWorks、Nastran、Ansys 和TOSCA 等）均集成了相應的優化設計模塊，這使船舶結構優化設計的應用日趨廣泛，解決的問題從減輕結構質量擴展到降低應力水平、改進結構性能和提高安全壽命等更多方面。例如：邱偉強等采用了SIMP法與BESO 法對VLCC 型單縱艙壁進行拓撲優化設計；朱俊俠等、楊玥等采用基于加權和法的多工況優化方法，分別對VLCC 型單縱艙壁、圓筒型FPSO 進行了拓撲優化設計。

由于現實中船舶領域的設計問題通常涉及多個不同工況。對于多工況下連續體拓撲優化設計問題的研究，多采用加權和法進行求解。它采用線性加權法將多工況問題轉化為單目標問題求解，實現容易，但對非凸優化問題來說，不能確保得到所有的Pareto 最優解。

折衷規劃法（Compromise Programming Method，CPM）已經被證明克服了加權和法的一些缺點：它能在Pareto 邊界的非凸區域上找到解。羅震等采用帶權重的CPM 針對優化過程中出現的棋盤格等問題進行了研究；范文杰等采用帶權重的CPM 對某三段式客車車架進行拓撲優化設計。盡管CPM 可以得到非凸區域上的Pareto 解集，但常規方法需要人為讀取優化設計時各個優化目標（如柔順度） 的最大值與最小值并進行標準差計算，再進行優化軟件的相關設置。整個流程中一旦相關設計約束改變，則需要重新對各目標剛度進行讀取與計算，耗費大量時間成本。

為此，本文基于CPM 提出了改進的折衷規劃法（Improved Compromise Programming Method，ICPM），并基于HyperMesh 軟件針對該方法進行了二次開發，以此向設計者提供一組智能Pareto 最優解決方案，節約優化設計的時間成本。應用該技術對海洋工程結構中某懸挑平臺縱向框架結構進行了多工況拓撲優化設計，并基于最終拓撲優化構型，從結構設計角度給出清晰的縱向框架構型。

1 折衷規劃法的改進

1.1 折衷規劃法數學模型

基于結構剛度最大化的拓撲優化是研究在設計域內得到使結構剛度最大（即柔順度最小）的材料分布形式的問題。每個工況對應一個剛度的最優結構拓撲，一般來說，不同的載荷工況將得到不同的結構拓撲。用帶權重的CPM表示多工況下剛度最大化（柔順度最小化）的目標函數：

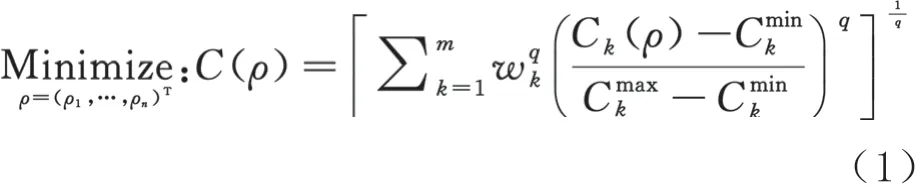
式中：，…，ρ為設計變量；為載荷工況總數；為單元總數；w為第個工況的權值；為懲罰因子，≥2；C（）為第個工況的柔順度目標函數；C、C為第個工況柔順度目標函數的最大值和最小值，N·mm。

1.2 改進折衷規劃法數學模型

由于傳統的折衷規劃法時間成本較高，本文提出一種改進的折衷規劃法：從設計之初開始，首先確定3個固定的體積分數約束，再分別在3種體積分數下進行單工況拓撲優化設計，并讀取出各體積分數約束下不同工況的最大和最小柔順度值，采用三點線性的方法近似擬合最大柔順度-體積分數約束折線與最小柔順度-體積分數約束折線。至此，若設計者想再采用其他體積分數約束時，就不必針對單個工況重新分析并讀取最大和最小柔順度值，只需根據三點雙線性插值即可得出各個工況近似的最大和最小柔順度值，然后立即進行拓撲優化設計而省去了重新計算各個工況的時間。由ICPM結合功效函數法可以得到如式（2）所示多剛度拓撲優化的數學模型：

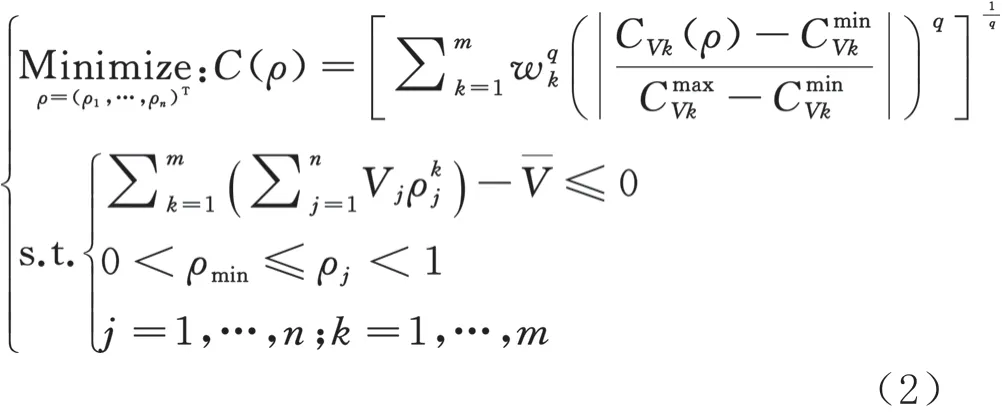
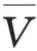
1.3 ICPM與CPM的時間成本對比

以重新優化設計次數（即重新變更體積分數約束的次數）為橫坐標，以時間成本為縱坐標。假定計算單工況分析所需要的時間為，計算各工況消耗的時間成本是一致的，工況總數為、優化設計次數為，則CPM進行優化設計所需要的時間為，ICPM進行優化設計所需要的時間為3。很明顯，當優化設計次數大于3次時，ICPM極有效地節約了時間成本；而當工況數較多，優化設計次數也越增越多時，ICPM節省的時間成本還會更多。

假定有5個工況，單工況所需的時間成本為2 min，總時間成本-優化設計次數的折線圖見圖1。

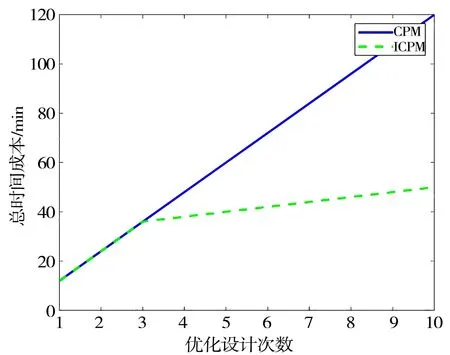
圖1 CPM與ICPM的時間成本對比

由圖1可見：隨著優化設計次數的增加，ICPM相比于CPM節約了大量的時間成本；隨著工況、單工況時間成本、優化設計次數的增加，會節約更多時間成本。

1.4 ICPM直接計算驗證

為了驗證CPM與ICPM在相同的體積分數約束下拓撲優化時均能產生相似的拓撲優化構型，本節采用簡單C形板計算模型（見圖2）針對ICPM合理性驗證。

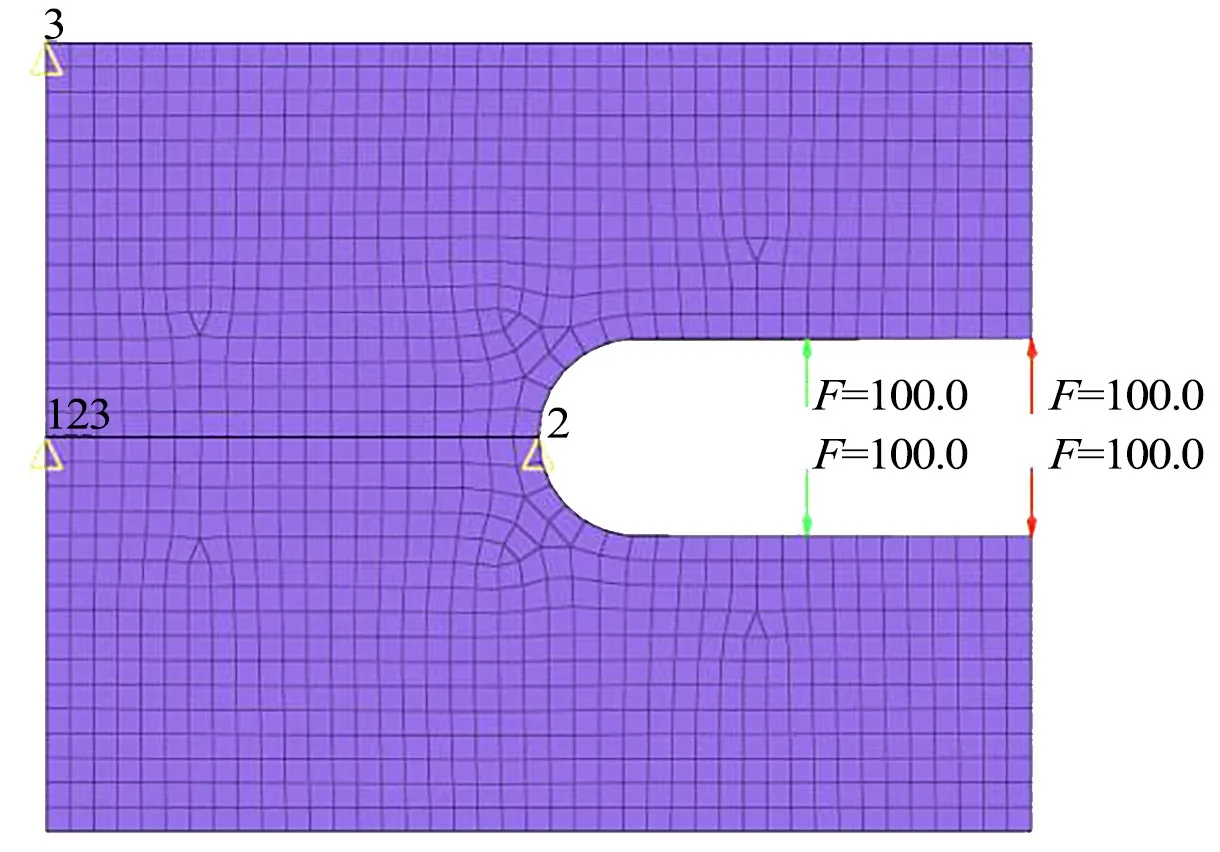
圖2 C形板

工況1載荷沿C形板端部布設（紅色標識），工況2載荷沿C形中部布設（綠色標識）。選取體積分數約束為0.30，工況1/工況2權重系數分別取0.40/0.60。拓撲優化結果見圖3。

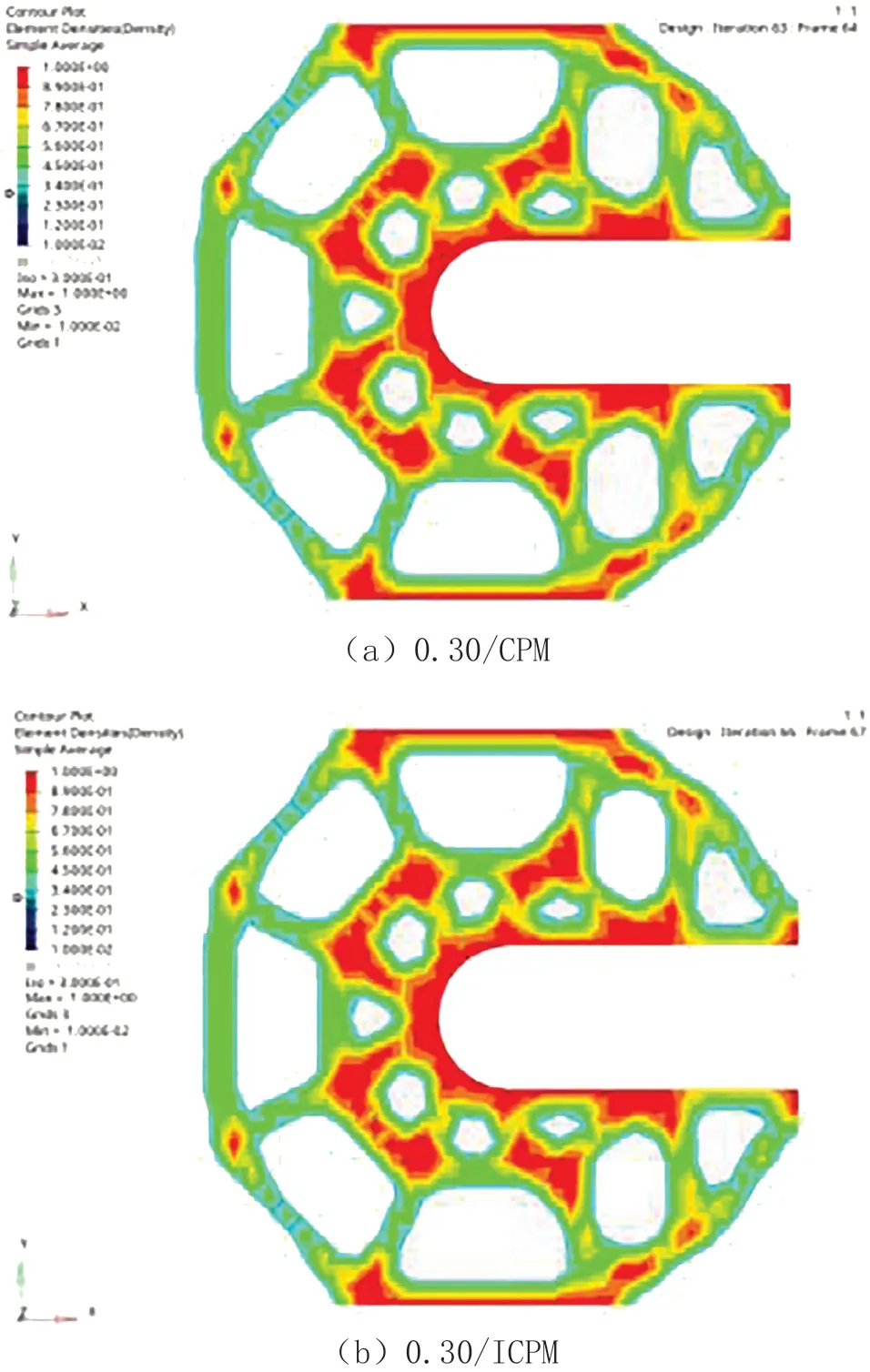
圖3 CPM與ICPM優化結果對比

由圖3可知：采用雙線性插值方法得到的最大和最小柔順度所構成的多工況化一的ICPM與CPM可得到幾乎一致的結果，由此也近一步證明了ICPM的合理性。拓撲優化本身對應著概念設計階段，在保證構型基本一致的前提下，ICPM最大限度地節省了設計的時間成本，進一步證明了其優越性。

2 改進折衷規劃法的二次開發

2.1 ICPM二次開發的主要思路

HyperMesh是Altair公司旗下一款優秀的有限元前處理軟件，有著良好的二次開發環境。通過TCL/TK語言，用戶可以編寫實現特定功能的TCL/TK函數；與此同時，HyperMesh也提供豐富的集成化的內部函數，用戶只需要在自己編寫的TCL函數中按照指定格式引用這些函數，就可實現某些模塊化的功能，比如單元屬性的讀取、外部文件的讀寫以及外部執行程序的調用等。

基于ICPM的多工況拓撲優化程序二次開發的主要思路（見圖4），首先設立相關界面按鈕，記錄多工況的數量及名稱；其次需要讀取各工況的結果文件，獲取各工況的最大和最小柔順度，并計算目標體積分數約束下近似柔順度的最大值與最小值，為后續編寫折衷規劃函數打下基礎；然后需要編寫Dequation自定義函數卡片，并創建DRESP2響應（第二類函數響應）；最終設定該函數響應為目標函數，將多工況拓撲優化問題轉換為單一目標拓撲優化問題。

圖4 ICPM二次開發的主要思路

2.2 ICPM程序的主要功能

改進的折衷規劃法（ICPM）二次開發程序主要包括4個子程序：

（1）讀取柔順度結果子程序，其主要功能是讀取優化結果out文件中的最大和最小柔順度值；

（2）計算柔順度子程序，其主要功能是根據已讀取的3個不同體積分數約束下的最大和最小柔順度，進行雙線性插值估算目標體積分數下的最大和最小柔順度；

（3）創建Dequation函數子程序，其主要功能是根據各個工況的最大和最小柔順度自動創建折衷規劃函數；

（4）創建響應函數子程序，其主要功能是根據折衷規劃函數，設置DRESP2函數響應卡片，對應各數值的實際含義，創建將多工況問題化為單一目標問題的響應，并設為拓撲優化迭代時的目標函數。

2.3 ICPM程序的用戶化界面

ICPM程序界面及操作步驟如圖5所示。

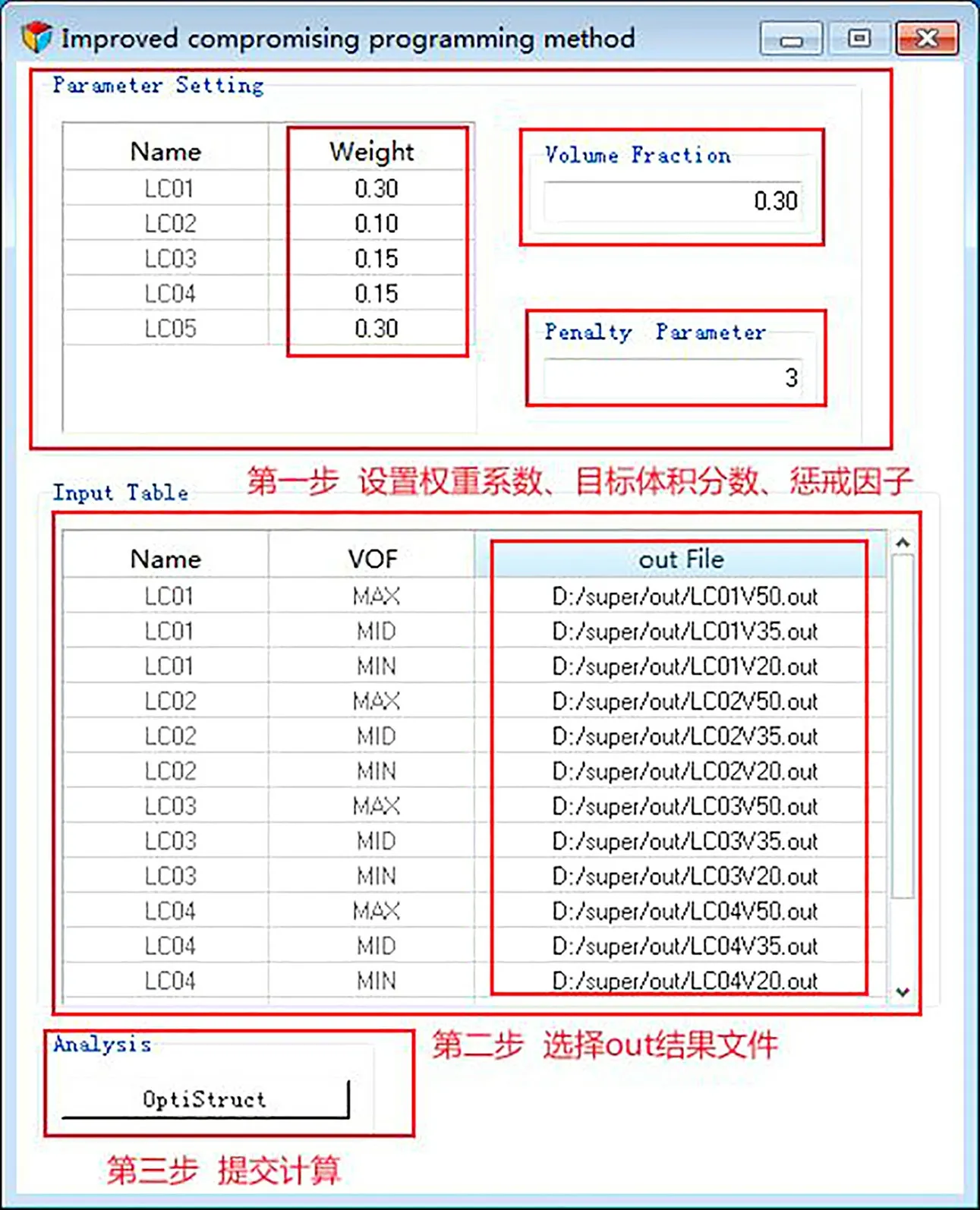
圖5 ICPM程序界面及操作步驟

界面的中Parameter Setting模塊用于用戶設置不同工況權重系數的區域；Volume Fraction模塊用于用戶設定所需要的目標體積分數約束；Penalty Parameter 模塊用于用戶設置懲戒因子，程序默認取3；Input Table模塊用于用戶選擇不同體積分數約束下各工況的out結果文件分別針對最大、中間和最小柔順度；Analysis模塊用于提交計算。

ICPM程序在使用上需先確定權重系數、目標體積分數、懲戒因子，接著再選擇各單工況分析結果out文件，最終提交計算。

3 結構多工況拓撲優化

3.1 懸臂平臺結構有限元模型

海洋工程結構中某平臺的有限元模型（隱去甲板），如圖6所示，淡藍色為邊界條件。

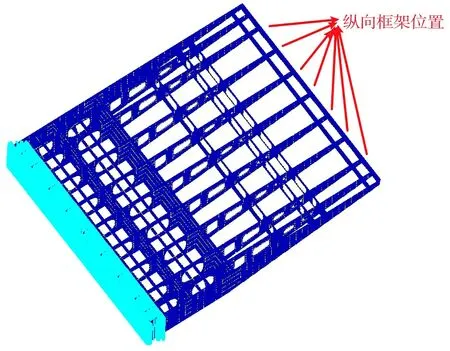
圖6 模型縱向框架所在位置

平臺模型中板材采用四邊形和少量三角形板殼單元模擬，骨材采用梁單元模擬。平臺材料均采用低碳普通鋼。

3.2 平臺結構拓撲優化設計域定義

根據實際工程受力情況，不將平臺頂板作為拓撲優化的對象；按照簡化工藝的要求，強框間距和縱骨間距通常取值固定，不作為拓撲優化的宏觀對象。

平臺縱向框架作為平臺內的主要支撐構件，主要承受頂板等支撐構件傳遞而來的載荷。由于平臺縱向框架分布較廣、占整個平臺結構體積較大，會影響其他構件的柔順度，故對其展開拓撲優化能夠較大幅度地改善整個貨艙區的應力分布。因此，本文選擇的拓撲優化對象為平臺縱向框架。

為了提高優化效率，選取中部所有縱向框架設置模式重復制造約束，要求所有中部縱向框架拓撲優化結果一致，拓撲優化縱向框架位置如圖6所示。

為了保證拓撲優化傳力路徑清晰，首先需要將原來構件中存在的開孔進行填實，然后需將縱向框架上所有布設的骨材刪除并折算到縱向框架板殼單元的厚度中；除此之外，為保證縱向框架與其他支撐構件的連接性，還需在縱向框架設定最小厚度的非設計區域。

3.3 拓撲優化工況及權重確定

為使拓撲優化結果更貼合實際，本文拓撲優化設計時考慮平臺實際的受力情況，分別設定了5個工況，主要分為受均布載荷及受集中載荷。權重系數根據各工況實際的危險程度進行大致評估。拓撲優化載荷布設及各工況權重系數見表1。

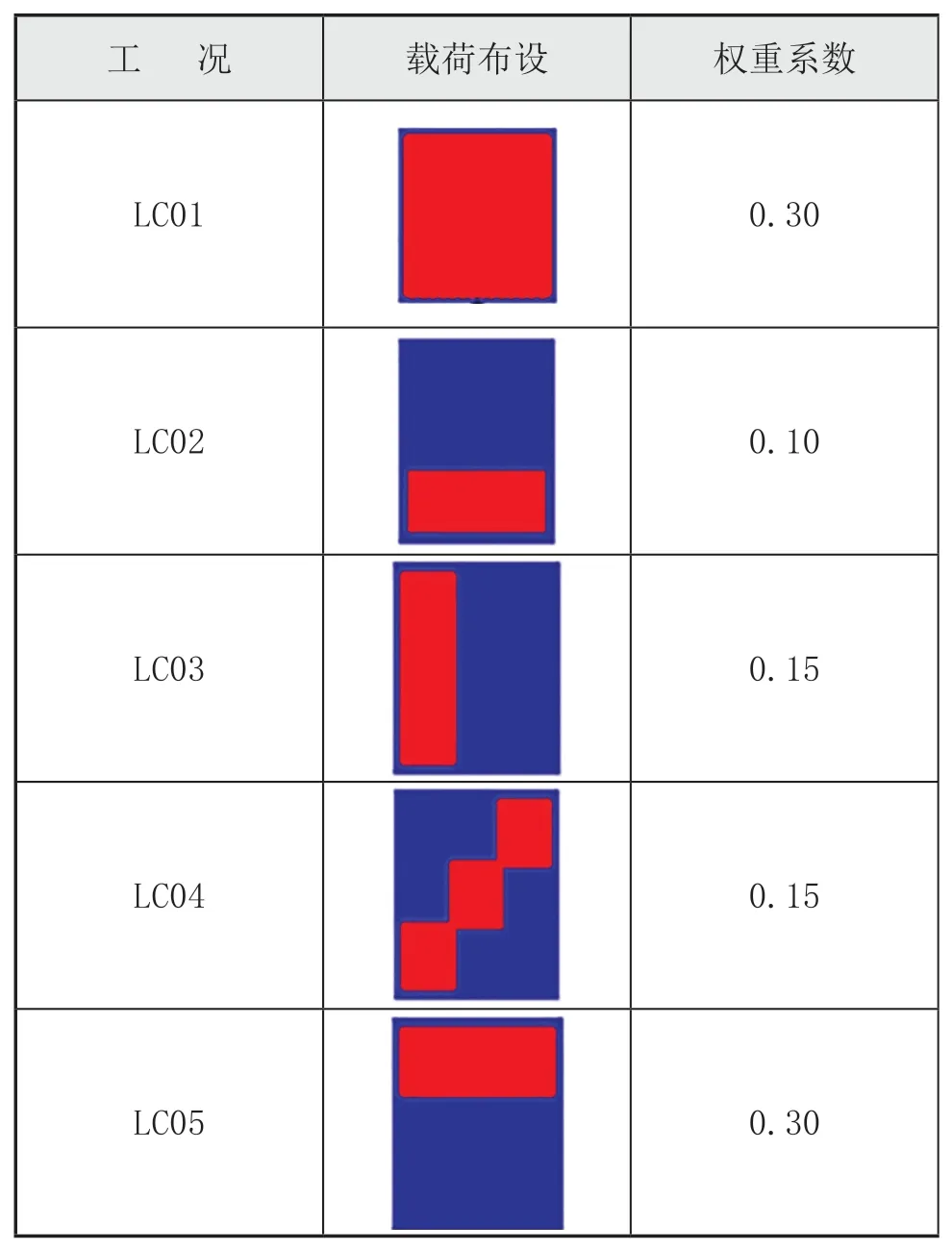
表1 拓撲優化工況及權重（俯視）

3.4 各單工況拓撲優化設計結果

設定不同體積分數約束0.50/0.35/0.20進行各單工況拓撲優化設計，可以得到不同載荷下，縱向框架對應的傳力路徑，為后續多工況拓撲優化提供支持，具體結果如表2所示。

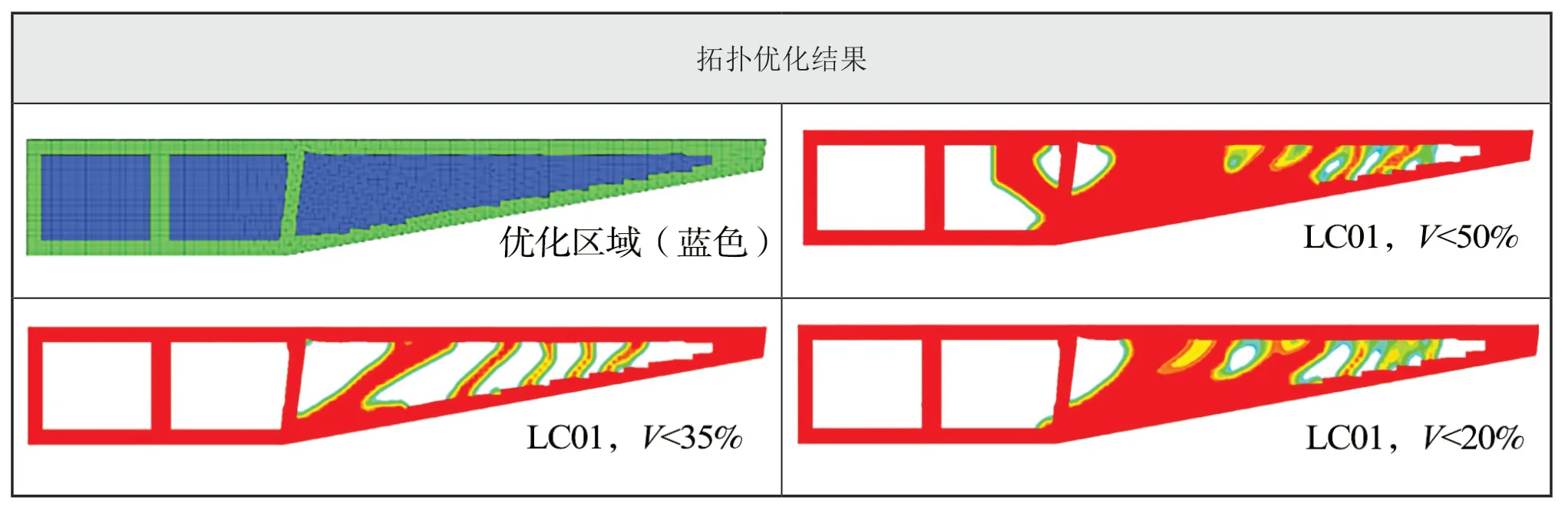
表2 不同體積分數約束0.50 / 0.35 / 0.20 下的各工況拓撲優化結果

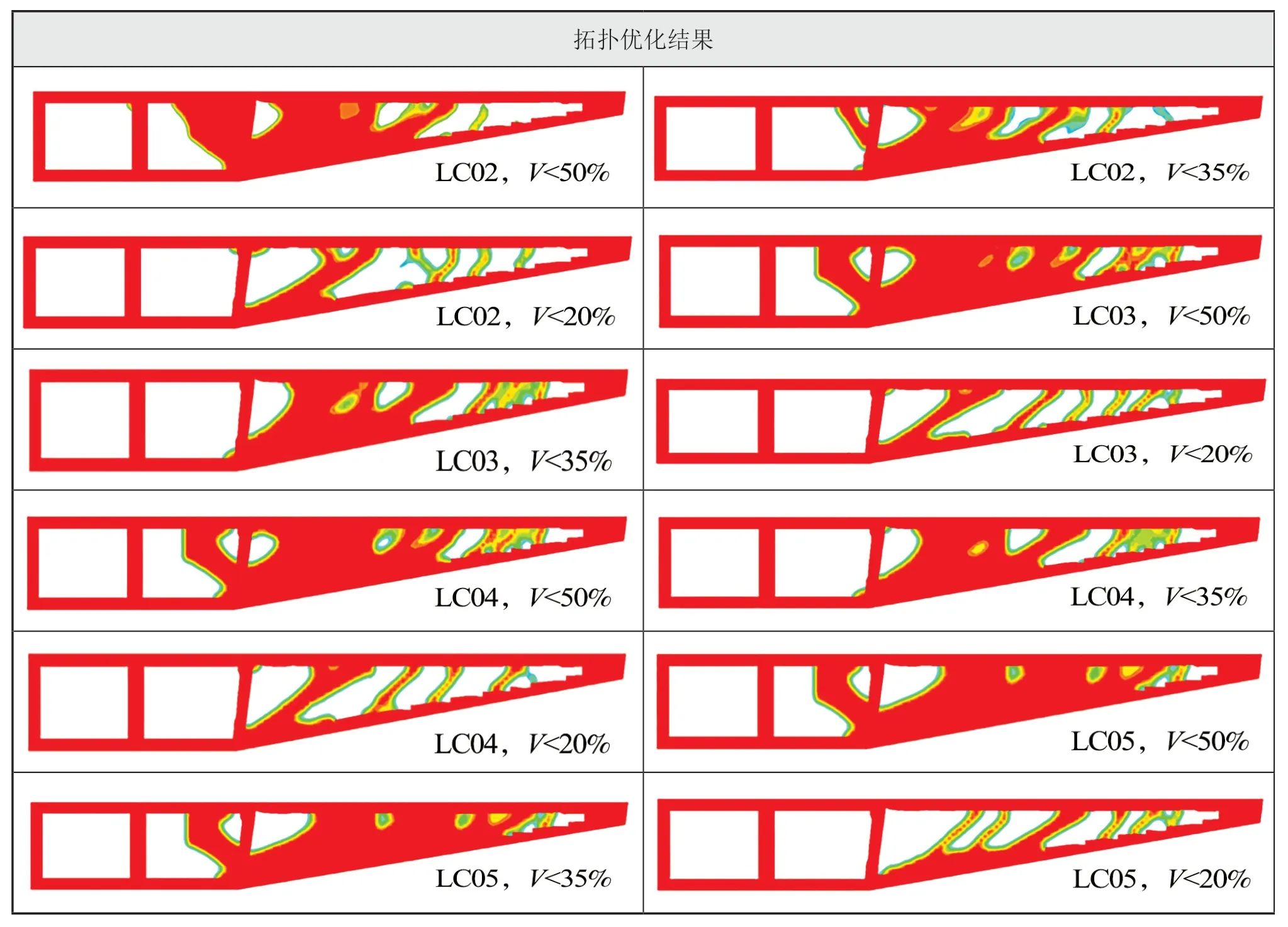
續表2

3.5 各工況結構柔順度表

各工況下，結構最大和最小柔順度見表3。

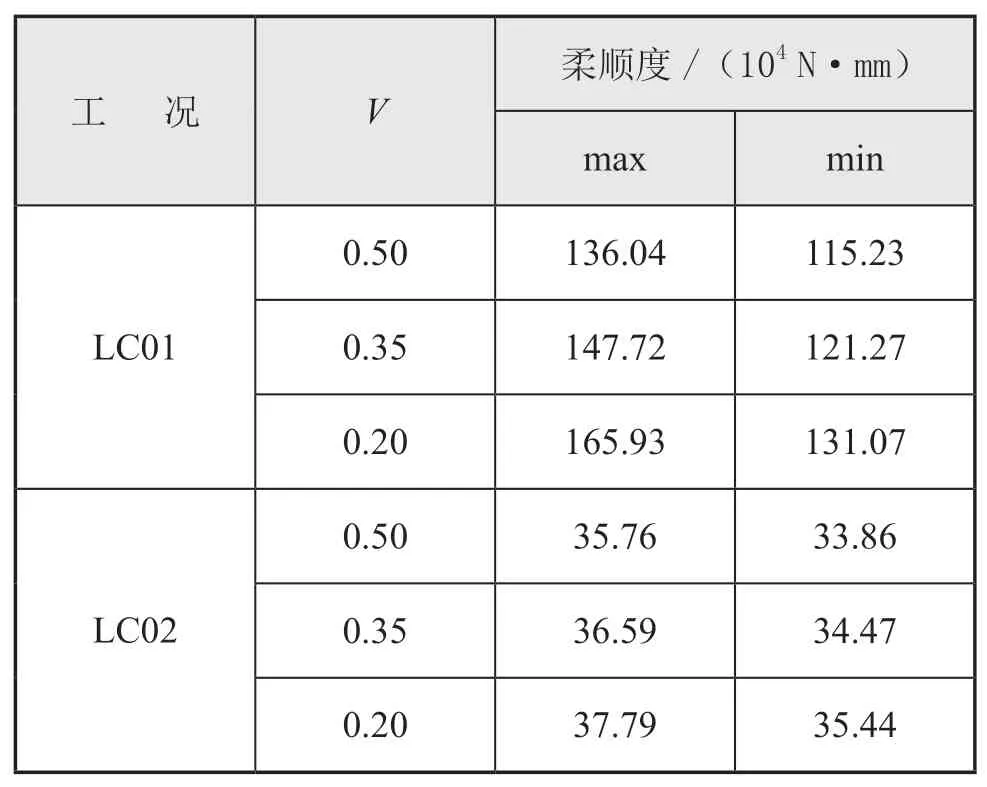
表3 各工況最大和最小柔順度表

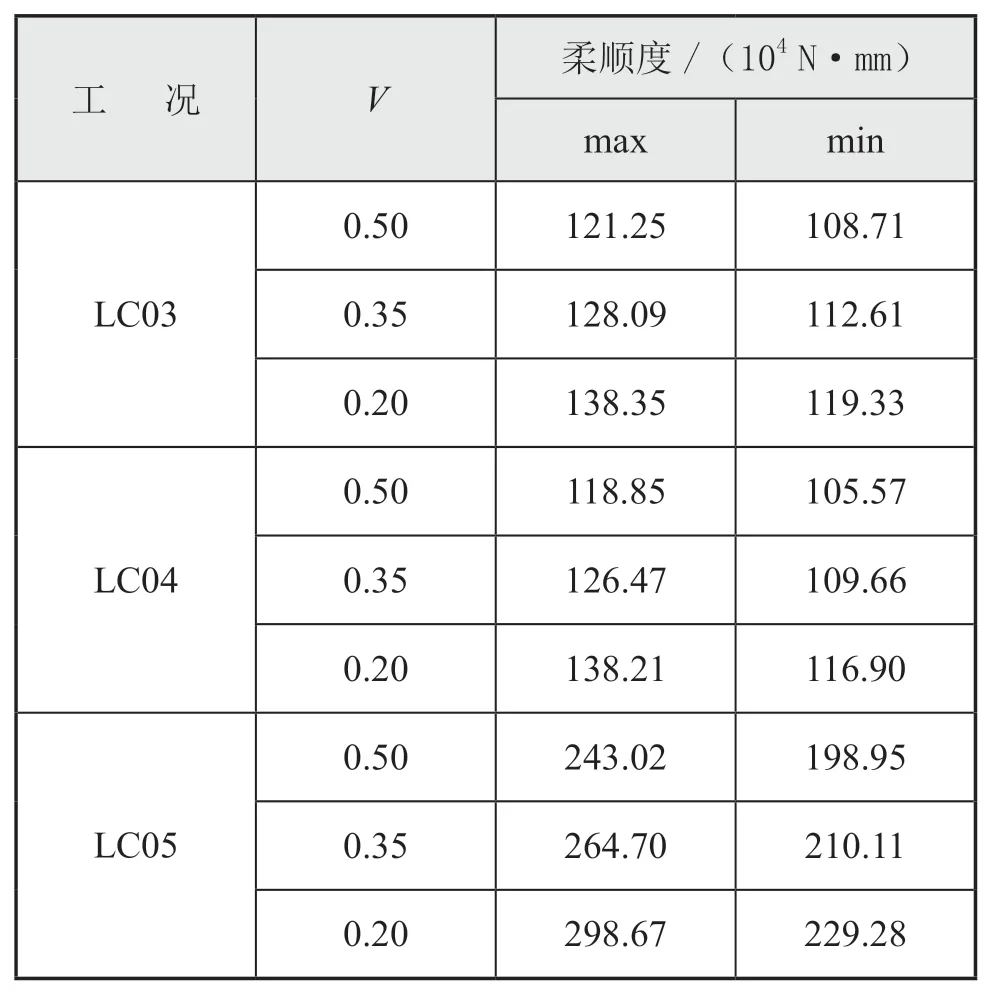
續表3

3.6 不同體積分數約束下拓撲優化結果

通過各工況最大和最小柔順度表，采用二次線性的方法可以簡單計算出不同體積分數約束下的最大和最小柔順度值，從而省去了各工況再次單獨分析的時間。最終針對不同體積分數約束（0.40/0.35/0.30/0.25/0.20），進行了多工況拓撲優化設計，單個工況拓撲優化設計大致為2 min。考慮上述多工況問題，采用CPM需要60 min，而采用ICPM則僅需36 min。

不同體積分數約束的拓撲優化結果見表4。從表4拓撲優化結果可得：不論何種體積分數下，縱向框架端部結構的單元密度基本趨于0，在結構設計時可考慮針對該區域進行適當開孔；縱向框架中部結構也具有明顯的可開洞趨勢；隨著體積分數的減少，縱向框架的尾部結構也逐漸有明顯的斜桿出現，可考慮在相應位置設置斜撐或扶強材。

表4 不同體積分數約束下多工況拓撲優化結果

基于0.20 體積分數約束下的拓撲優化結果，本文給出了經拓撲優化后的縱向框架最終設計圖，并與拓撲優化前的縱向框架初始設計圖紙進行了對比，如表5 所示。

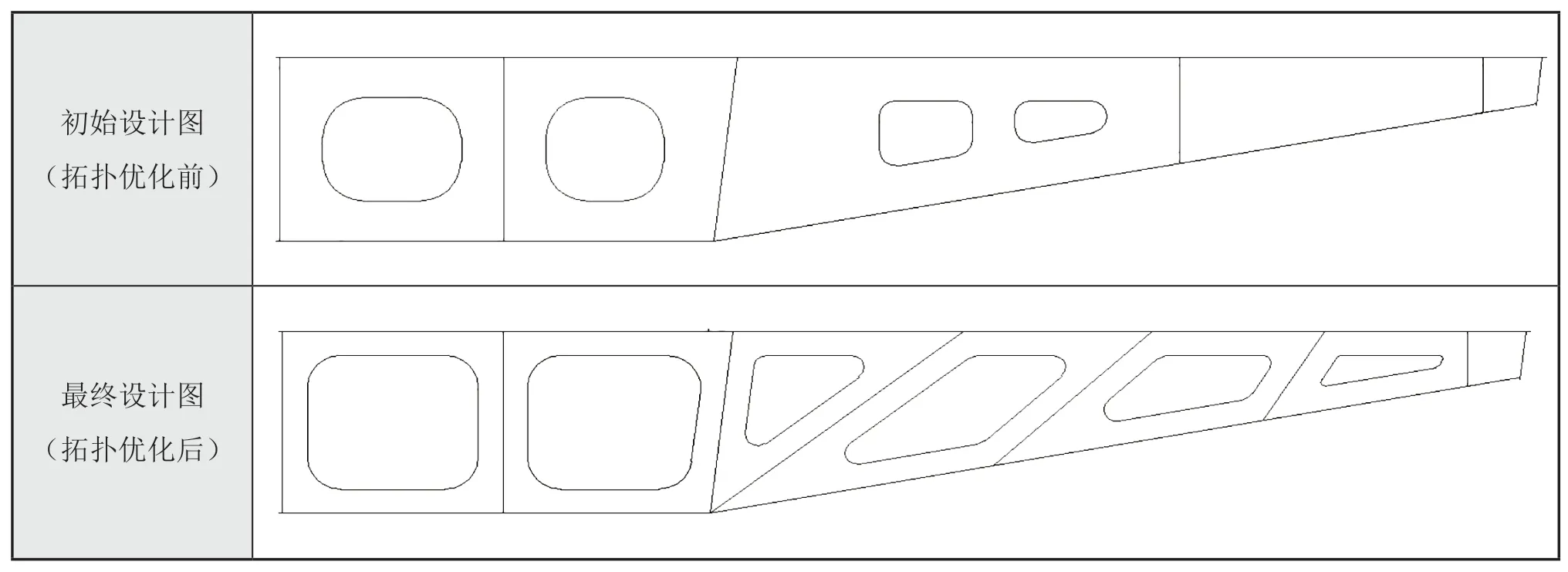
表5 拓撲優化前后縱向框架設計圖對比

3.7 不同構型下結構柔順度、強度對比

基于縱向框架最終設計圖，針對模型縱向框架結構部分進行了模型重建，通過設置Compliance響應，讀取了各工況下結構的柔順度，并與實心結構（縱向框架填實）、初始設計結構進行了柔順度對比，見表6。

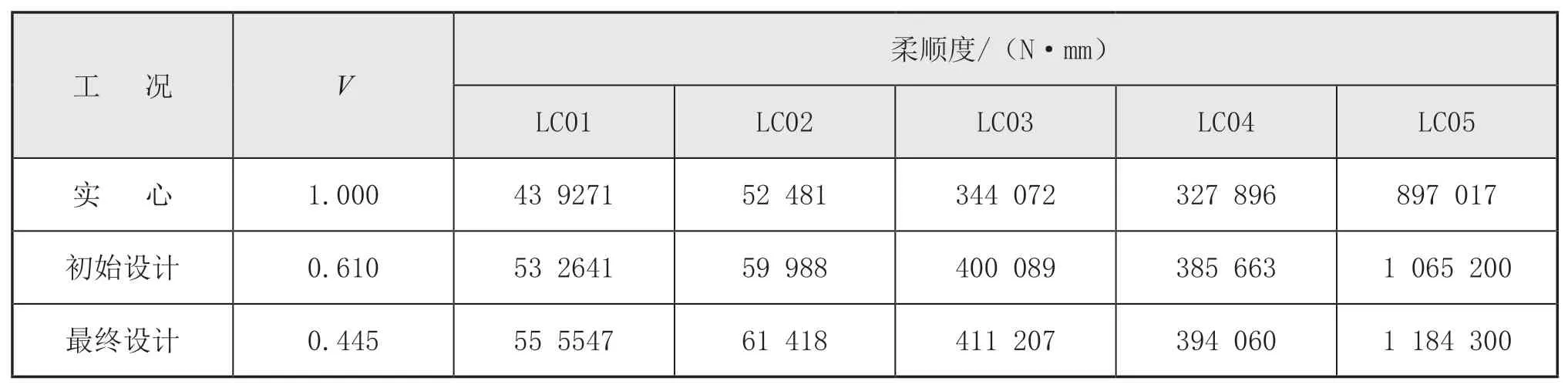
表6 不同構型下結構柔順度對比

為使優化結果更加直觀，讀取了3 種設計構型下Von Mises 應力進行強度對比，見表7。

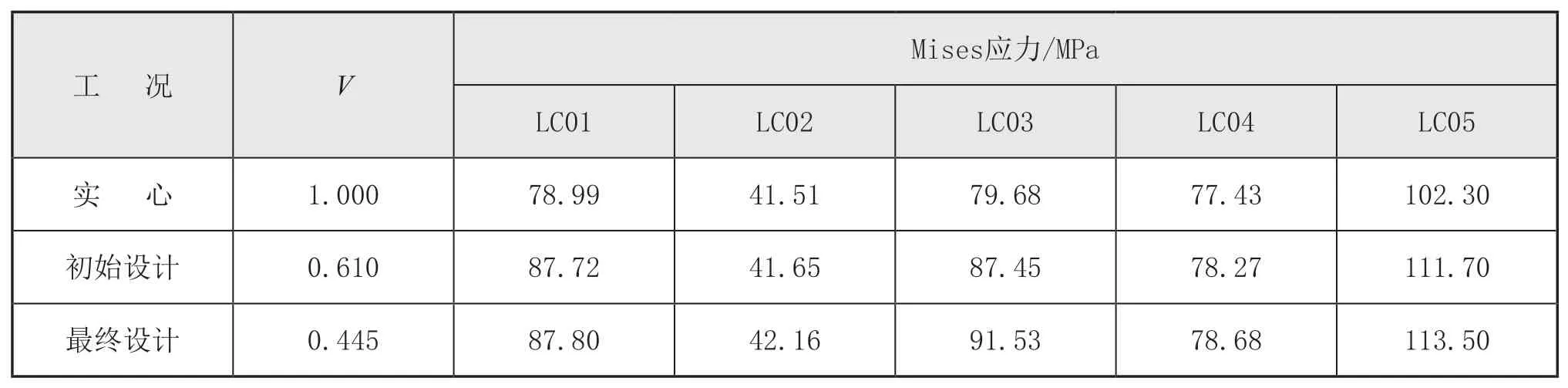
表7 不同構型下結構Mises 應力對比

由表6 和表7 可見，最終設計結構構型相比于初始設計的體積分數降低16.5%，且結構的柔順度、Mises 應力增加幅度并不明顯，進一步證明了拓撲優化方法的必要性與優越性。

4 結 語

本文提出了改進的折衷規劃法，并基于Hyper Mesh/OptiStruct商用軟件平臺進行了改進折衷規劃法的二次開發。應用表明:該方法和軟件能夠幫助設計者找到更為清晰的傳力路徑，操作性好，可有效節省優化設計的時間，提高工作效率。