水文模型不確定性研究方法耦合分析

鄭言峰

(青島市水利勘測設計研究院有限公司，山東 濟南 250013)

水文模型的不確定性評價已經成為水文學者研究的熱點問題之一[1-4]。水文模型不確定性的來源是多方面的，總體上可以分為以下3類：實測資料(降雨、蒸發、徑流等)的不確定性、模型結構的不確定性以及模型參數的不確定性。為了綜合分析以上因素對模型不確定性的影響，Beven和 Binley[5]于1992年提出了通用似然不確定性估計方法，即GLUE方法。該方法將Monte Carlo隨機取樣技術與Bayesian理論結合起來，原理簡單，易于操作。然而，GLUE方法在很多實際應用中的結果[6]表明預測區間的覆蓋率遠低于給定的置信水平。XIONG等[7]通過引入“模擬偏差曲線”對GLUE方法進行了改進，在一定程度上提高了區間覆蓋率，但同時也增加了區間帶寬。

數據同化方法將模型和觀測這兩種研究手段進行了結合[8]，從而實現了在觀測資料更新的同時可以更新模型的計算結果。它的主要思想是將最新的觀測數據融合到所使用的模型之中，通過不斷更新的觀測數據來減小狀態變量模擬誤差，繼而使用更新之后的狀態變量重新預報從而來達到提高預報精度的目的。作為數據同化方法的典型代表，集合卡爾曼濾波(Ensemble Kalman Filter，EnKF)已被廣泛應用到海洋、陸面和大氣數據同化領域之中[9]。EnKF方法融合了蒙特卡洛(Monte Carlo，MC)采樣技術，可以分別考慮模型觀測資料的不確定性以及模型結構的不確定性。2005年，Moradkhani等[10]在EnKF的基礎上又加入了模型參數的更新(即dual EnKF)，用以描述模型參數的不確定性。

為了探索解決在提高區間覆蓋率的同時降低預測區間平均帶寬問題，本文將dual EnKF方法與GLUE方法2種水文模型不確定性研究方法進行了耦合，得到了dual E-G方法，并以新安江模型為例，研究了dual E-G方法在漢江上游3個子流域(即甲河流域、天河流域和灞河流域)中的適用性。該成果可為水文模型預報、洪水決策風險分析等方面的深入研究提供有益參考。

1 研究區概況

漢江又稱漢水，是長江中下游最大的一條支流，發源于秦嶺南麓，干流流經陜西和湖北兩省，于武漢市匯入長江。漢江干流全長1 570多km，流域面積大約15.9萬km2。干流丹江口以上為上游，流域面積大約9.5萬km2。漢江流域河流密布，溝壑交織，分布著大小河流及山溝數以千計。漢江流域幅員廣闊，光、熱和水資源空間差異比較大，氣候特征多變，其降水主要來源于東南、西南2股暖濕氣流，因此降水變率比較大，是中國旱、澇災害多發的地區之一。作為南水北調中線工程水源地的丹江口水庫，不僅承擔著湖北武漢、襄陽等23個縣市1億多人口及124萬多hm2耕地的防洪任務，還承擔著河南、河北、北京、天津等四省市的20多座城市的供水任務，意義重大。但是21世紀以來，漢江流域出現的干旱問題，嚴重影響了流域內的生態環境與供水工程。研究漢江流域上降雨徑流模擬的不確定性，不僅可以為決策者提供充足的風險信息，還可以實現水資源的合理配置，從而保證南水北調中線工程的順利實施。

因此，選擇了漢江上游的3個子流域(即甲河流域、天河流域和灞河流域)作為研究對象。3個子流域均為濕潤地區，且資料長度均為8年。前5年(1980—1984年，共1 827天)的流域實測平均日降雨、日蒸發和日徑流作為率定期，后3年(1985—1987年，共1 095天)的流域實測平均日降雨、日蒸發和日徑流作為檢驗期。流域水文資料的具體情況見表1，3個子流域在漢江中的位置及流域見圖1。

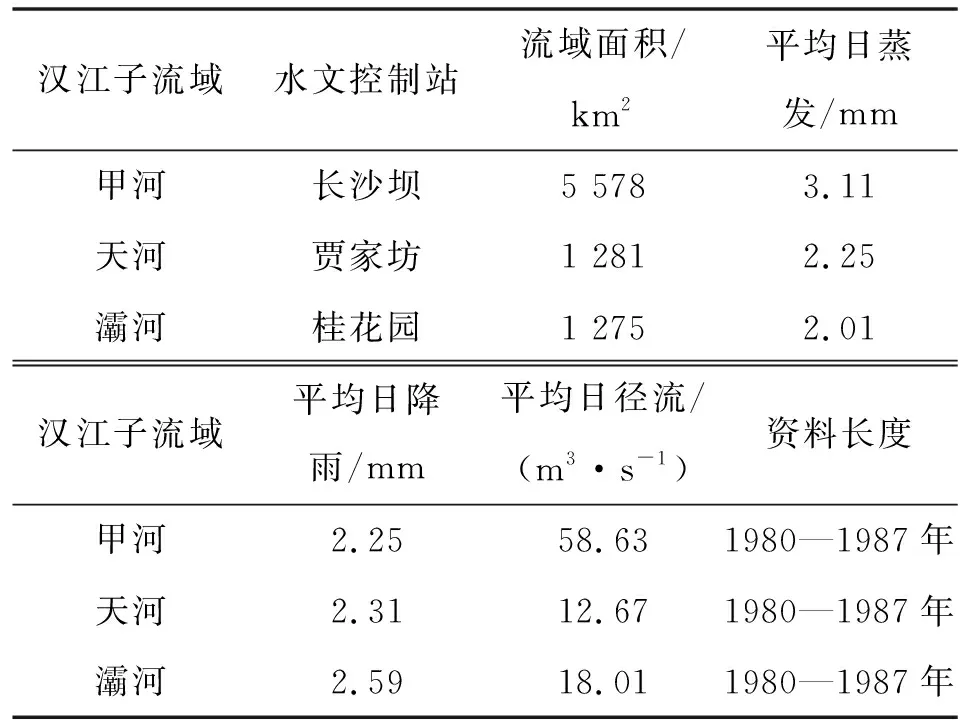
表1 研究流域資料

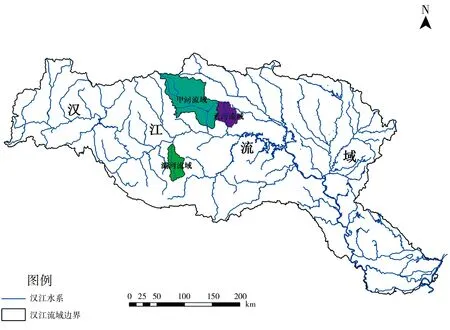
圖1 甲河、天河及灞河在漢江中的位置及其流域

2 模型簡介及評價指標

2.1 新安江模型簡介

對于研究水文模型的不確定性而言，概念性水文模型優于系統模型和物理模型。概念性模型主要利用一些簡單的物理概念和經驗公式，來近似描述水流在流域的運動狀態。系統模型主要是將所研究的流域或區間看作一種動力系統，利用輸入與輸出資料，建立某種數學關系，這種模型只關心模擬結果的精度，并不考慮輸入與輸出之間的物理關系。物理模型主要根據水流連續方程和動量方程來求解水流在流域的時間和空間變化規律，雖然模型物理意義更加明確，但其對資料要求過于嚴格，一般流域很難滿足。

新安江(三水源)模型是河海大學(原華東水利學院)趙人俊等在1973年提出來的降雨徑流模型，簡稱新安江模型。由于新安江模型采用蓄滿產流進行產流計算，因此主要適用于濕潤、半濕潤地區。近幾十年，新安江模型不斷改進，已成為中國應用較為廣泛的一個流域水文模型。

新安江模型作為國內常用的一種概念性水文模型，大部分模型參數都具有明顯的物理意義，不僅模擬精度高，而且對水文資料的要求比較低，對于日模型來說，只需要流域日蒸發資料、日降雨資料以及日徑流資料即可。新安江模型共有15個模型參數。①K：流域蒸散發能力Ep與蒸發皿實測值EM之比，簡稱蒸散發折算系數；②IMP：一般將整個流域面積分為透水面積與不透水面積，IMP是指全流域面積中不透水面積所占的比例；③B：蓄水容量曲線的指數；④WUM：流域上層蓄水容量(mm)；⑤WLM：流域下層蓄水容量(mm)；⑥WDM：流域深層蓄水容量(mm)；⑦C：深層蒸散發系數；⑧SM：自由水蓄水容量(mm)，反映表層土蓄水能力的大小，直接決定著地面徑流和地下徑流所占的比重；⑨EX：自由水蓄水容量曲線的指數；⑩KG：地下水出流系數；KI：壤中流出流系數，主要取決于表層土的滲透性；CG：地下徑流的消退系數，反映地下徑流的消退規律；CI：壤中流的消退系數，反映壤中流的消退規律；nn：反映流域調蓄能力的參數，相當于線性水庫的個數或水庫的調節次數；KK：線性水庫的蓄泄系數，相當于流域匯流時間的參數，具有時間因次。

2.2 似然函數的選擇

在對水文模型進行率定時，需要定義一個評價模擬實測流量好壞的標準，即似然函數。似然函數必須滿足一定的特點：當模擬系列與實測系列沒有相似性時它的值應為0，并且相似性越高，它的值應越大。不同的似然函數率定得到的參數也會有所不同，有的似然函數對高水的模擬效果較好，有的似然函數對低水的模擬效果較好，而納西效率系數因對整體模擬效果較好而被廣泛應用于水文模型參數估計研究中。因此，采用納西效率系數R2作為似然函數，表達見式(1)：

(1)

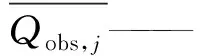
當R2的值等于1時，模擬流量序列完全重現了相應的實測流量序列，此時的模擬效果最好；當R2的值等于0時，模擬流量序列對同期觀測的擬合程度與實測流量序列長時間尺度上的平均值對實測流量序列的擬合程度相當；R2的值越小，模型模擬的序列對相應觀測的擬合程度越差[11]。

2.3 預測區間評價指標

為了反映水文模型模擬和預報實測流量的不確定性，每個實測流量的預測結果不應該只是單純的點估計，而應該是給定置信水平下的區間估計。XIONG等[12]從區間覆蓋率、區間帶寬和區間不對稱性3個方面詳細介紹了7個用于評價預測區間好壞的指標。因此，從3個方面中各選擇一個比較常用的指標(區間覆蓋率、平均帶寬和平均不對稱程度)來評價預測區間的性質。它們的定義如下。

a)區間覆蓋率(CR)。區間覆蓋率是指實測流量落入預報區間的個數與實測流量數據總個數的比值。自從Beven提出GLUE方法以后，區間覆蓋率就被廣泛應用于評價預測區間的好壞。CR越大，表示預測區間覆蓋率越高，CR最為理想的值為1，這意味著預測區間覆蓋了所有的實測流量數據。

b)平均帶寬(B)。平均帶寬是所有流量的預測區間上下界差值的平均值，單位：m3/s。

(2)

QU(j)、QL(j)分別表示第j時刻的流量預測區間上下界。對于指定的置信水平，在保證有較高的覆蓋率前提下，預報區間的平均帶寬越窄越好，此時的預測區間的不確定性也較小。

c)平均不對稱程度(S)。

(3)

理想的預測區間是不僅能覆蓋大部分的實測流量，而且預測區間的平均帶寬值較小，并且預測下界與實測流量之間的距離近似等于預測上界與實測流量之間的距離。

3 不確定性研究方法

3.1 GLUE方法

GLUE方法中的一個很重要的觀點是：導致模型模擬結果好壞的不是模型單個參數，而是模型的參數組合。目前GLUE方法已成為水文模型不確定研究的主流方法[1-3,13-14]。GLUE方法的主要思路如下：選定模型及似然函數，并設定似然閾值；在預先設定的參數分布(一般假定為均勻分布)取值空間內，利用Monte Carlo隨機取樣獲得一定數量的有效參數組(即似然函數值高于似然閾值的參數組)；在給定的置信水平下，求出每個實測流量的預測區間。

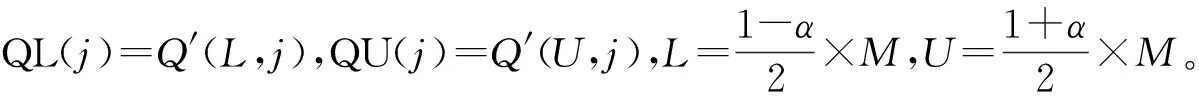
GLUE方法共有3個參數，即似然函數閾值TH、有效參數組的個數M、置信水平α。每個參數的取值如下：TH=0.5，M=2000，α=0.8。

3.2 dual EnKF方法

在EnKF方法中假定水文模型的參數不隨時間變化，模型的參數可以通過模型率定獲得。但是由于模型驅動數據和觀測數據存在一定誤差，不能保證模型的模擬效果不會隨著時間的變化而有所差異。因此，有必要將模型參數的更新納入預報的過程之中[10,15-16]。模型參數的更新過程類似于狀態變量的更新過程。

dual EnKF方法的具體步驟如下。

步驟一選擇水文模型，準備必要的驅動數據(流域平均日降雨資料P、流域平均日蒸發資料E)和流域實測日流量資料Q，確定一組有效參數組θ0。

步驟二確定集合成員個數N、日蒸發的測量誤差超參數γE、日降雨的測量誤差超參數γP和日徑流的測量誤差超參數γQ。

步驟三分別對日蒸發、日降雨和日徑流資料加上一系列高斯白噪聲擾動。

(4)

(5)

(6)

步驟四計算每個成員的狀態變量先驗值。

(7)

t=1時，

步驟五計算每個成員的模擬流量。

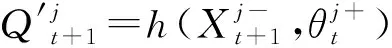
(8)

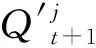
步驟六計算每個模型參數的增益。

(9)

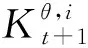
步驟七計算每個成員t+1時刻的模型參數更新值。

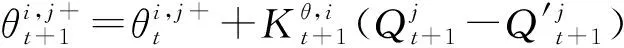
(10)

步驟八使用更新之后的模型參數重新計算狀態變量值。

(11)

步驟九使用更新之后的模型參數重新計算模擬流量值。

(12)

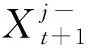
步驟十計算每個狀態變量的增益。

(13)

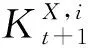
步驟十一計算每個成員的狀態變量后驗值。

(14)

dual EnKF方法共有4個參數，即集合成員個數N和3個超參數γE、γP、γQ。隨著集合成員個數N的增加，集合成員的代表性逐漸增強、分析誤差逐漸減小，但卻加重了計算負擔。因此，需要選擇一個合適的集合數既能滿足集合成員代表性的要求，又要考慮計算負擔問題[17]。超參數的大小直接影響著驅動數據和觀測數據誤差的大小。Moradkhani等[10]通過研究發現當N=50、γE=γP=γQ=0.1時，模擬效果較好。因此，本文中的4個參數的取值與Moradkhani的研究結果保持一致。

3.3 dual E-G方法

目前大多數基于GLUE方法的水文模型不確定性研究結果表明：隨著覆蓋率的增高，平均帶寬反而增大[7,12,14]，無法提供有效的決策依據。

為了探索解決在提高區間覆蓋率的同時降低預測區間平均帶寬問題，將dual EnKF方法與GLUE方法2種水文模型不確定性研究方法進行了耦合，得到了dual E-G方法。具體耦合方法如下：①首先按照GLUE方法產生似然函數大于閾值TH的M組有效參數組；②將每組模型參數產生的服從均值為參數本身，方差為參數的0.1倍的N個參數組作為每個成員的參數初始值；③然后按照dual EnKF方法進行模型參數更新；④最后將得到的N個模擬流量系列的均值作為該組參數的最優模擬系列，則M組有效參數組便得到M個模擬流量系列；⑤將M個模擬流量系列同一時刻的所有模擬流量Q(i,j)分別從小到大排序；⑥對于給定的置信水平α(0<α<1)，分別計算第j時刻實測流量的下界預測值QL(j)和上界預測值QU(j)。

4 實例計算與分析

為了分析耦合效果，以新安江模型為例，模型參數取值范圍見表2。對于給定的置信水平α(0<α<1)，采用3個評價指標(覆蓋率、平均帶寬和平均不對稱性)評價了dual E-G方法在3個流域(甲河、天河、灞河)的預測區間性質，并與GLUE方法進行了對比，見表3、4。由表4可知，相比于GLUE方法，dual E-G方法在甲河、天河和灞河流域中計算得到的率定期的區間覆蓋率分別提高了28%、41%和29%，平均帶寬分別降低了8%、18%和6%，平均不對稱程度分別降低了62%、75%和44%；檢驗期的區間覆蓋率分別提高了31%、53%和32%，平均帶寬分別降低了4%、1%和2%，平均不對稱程度分別降低了67%、80%和59%。綜上所述，dual E-G方法可以同時改善3種不確定性指標。

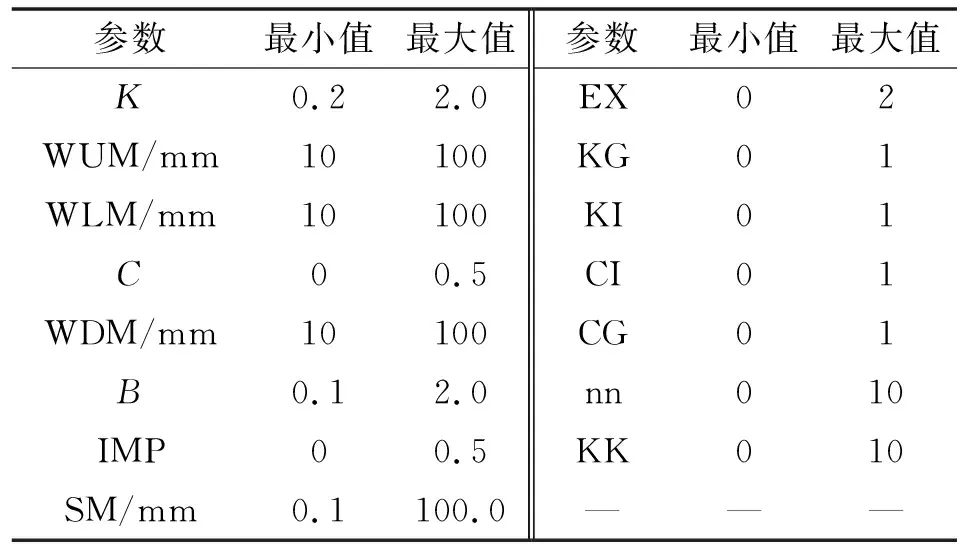
表2 新安江模型參數取值范圍

表3 GLUE方法和dual E-G方法在不同流域上的預測區間性質

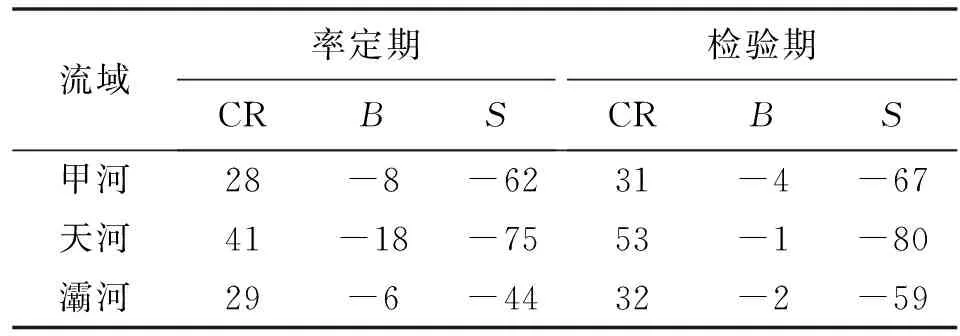
表4 dual E-G方法相比于GLUE方法的改善程度 %

為了便于比較不同方法計算出來的預測區間的性質，本文選用了甲河流域率定期中的1984年和檢驗期中的1985年的預測區間圖來比較GLUE方法和dual E-G方法預測區間的優良性，見圖2。可以看出，與GLUE方法相比，EnKF-G方法率定期模擬洪峰能力提高，檢驗期的低水部分模擬效果更好一些，且預測區間改善比較明顯，不僅提高了區間覆蓋率、降低了區間平均不對稱程度，還在一定程度上降低了平均帶寬。

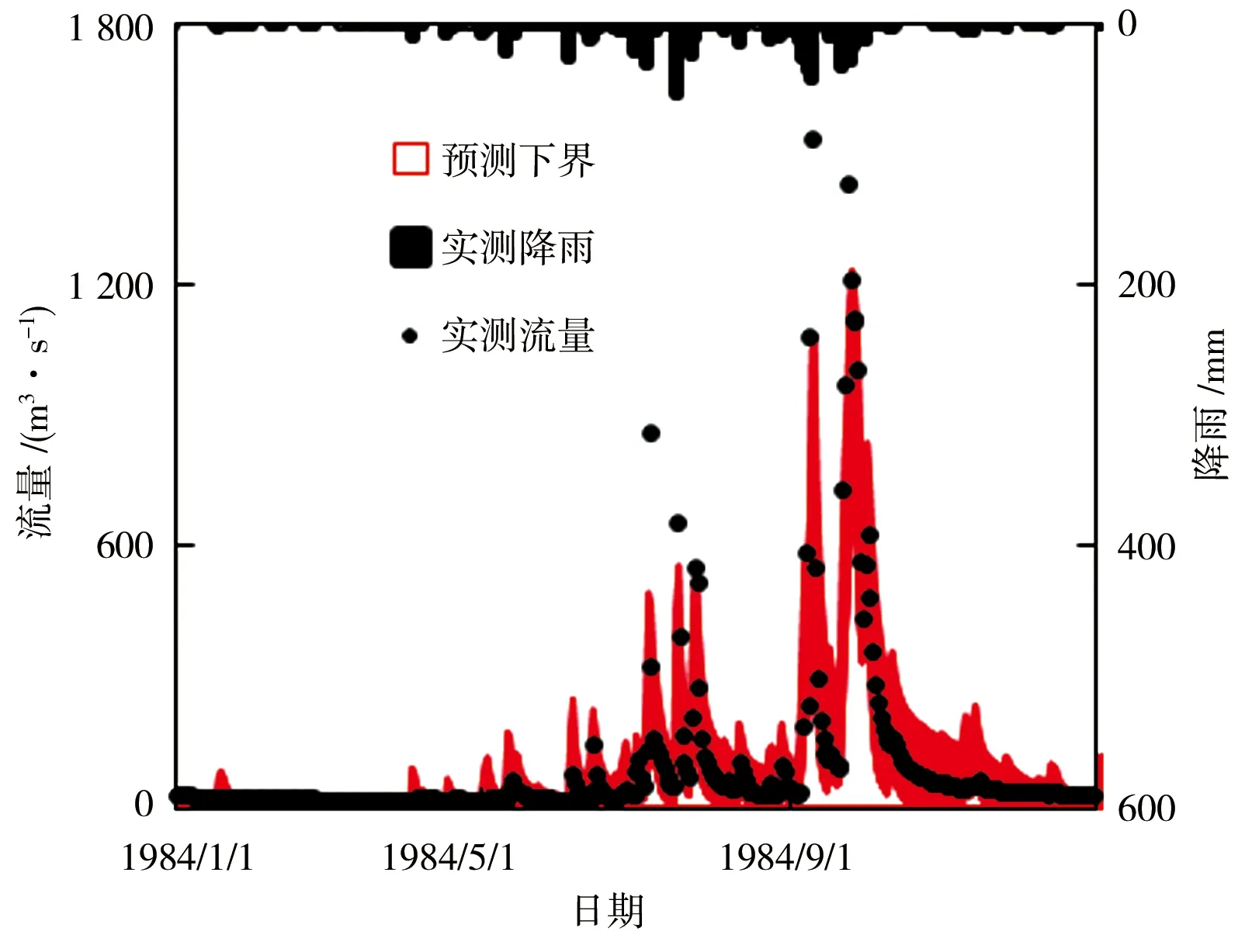
a)GLUE方法率定期

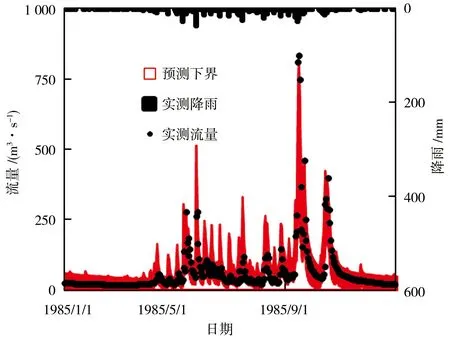
d)dual E-G方法檢驗期

為了說明dual E-G方法降低不確定性的原理，以GLUE方法篩選出的新安江模型的第1組有效參數為例進行分析。對于GLUE方法，直接采用第1組有效參數計算的模擬流量系列計算納西效率系數；對于dual E-G方法，將由第1組有效參數生成的服從均值為模型參數本身，方差為模型參數的0.1倍的50個參數組作為每個成員的初始參數組，然后再按照dual EnKF方法進行參數向量更新，從而計算出50個成員的模擬流量系列，將集合均值作為各時刻流量的最優預報值，組成最優模擬系列，進而計算納西效率系數，結果見表5。由表5可知，dual E-G方法模擬精度明顯高于GLUE方法，甲河流域率定期納西效率系數提高了0.26，達到了0.89；灞河流域檢驗期納西效率系數提高了一倍以上，達到0.62。

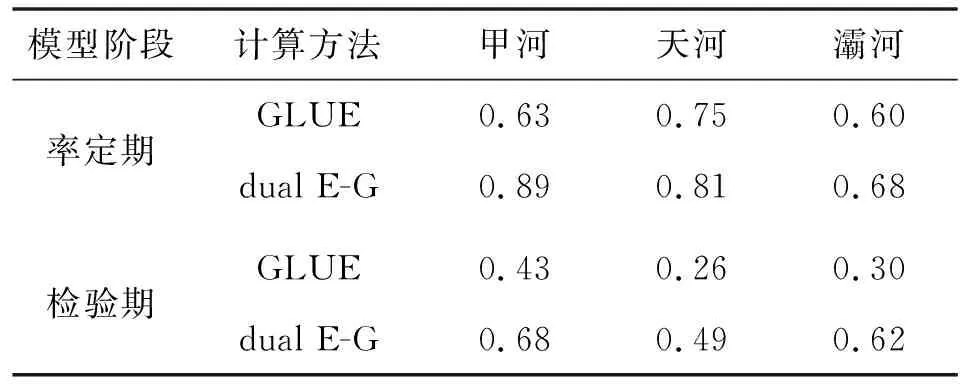
表5 第1組有效參數模擬系列納西效率系數對比

GLUE方法能夠充分考慮模型參數的空間不確定性，篩選出大于似然閾值的有效參數組，但是由于未能對參數進行實時更新，隨著時間的變化，模型參數的時間不確定性逐漸累積，導致模擬精度有所降低；dual EnKF方法能夠充分考慮模型參數的時間不確定性，對于給定位置的有效參數組能夠通過實時數據及誤差擾動進行不斷更新，以達到最優的模擬效果，但是無法體現下墊面變化導致的參數空間不確定性影響。dual E-G方法將GLUE方法考慮的模型參數空間不確定性與dual EnKF方法考慮的模型參數時間不確定性進行了充分結合，使得模擬效果更加接近實際，從而表現出更高的模擬精度和更優的預測區間。

5 結語

單純采用GLUE方法進行水文模型不確定性分析時不可避免地會產生以增加平均帶寬為代價來提高區間覆蓋率或以降低區間覆蓋率為代價來減小平均帶寬的問題，主要原因是由于“異參同效現象”的存在導致最優參數很難獲得。dual EnKF方法可以根據每個成員的狀態變量先驗值，通過迭代更新使得每組參數都能夠盡可能達到最優，從而提高每個成員的模擬效果。耦合后的dual E-G方法，能夠充分考慮模型參數的空間不確定性和時間不確定性，可以使得M組有效參數組都能夠盡可能達到最優，不僅可以提高模型預報精度，還可以改善預測區間性質，即可以同時改善區間覆蓋率、平均帶寬和平均不對稱程度。

以新安江模型為例，研究了dual E-G方法在漢江3個子流域上的適用性。該成果可為水文模型預報、洪水決策風險分析等方面的深入研究提供有益參考。然而水文模型的不確定性是一個非常復雜的系統問題，dual E-G方法在不同模型、不同流域上的適用性仍有待進一步研究。