散射體特征對隔聲超材料性能的影響
王前選,陳志民,吳玲玲,劉成沛,楊 藝,盧釗明
( 五邑大學 軌道交通學院,廣東 江門 529020)
截止至2020年底,我國高速鐵路總里程已達3.79 萬公里,居世界第一位[1],但高速鐵路的飛速發展也帶來了噪聲等負面問題[2],研究表明,列車噪聲在影響鐵路周邊環境的同時,也會對乘客及列車工作人員的身體健康產生危害,連續的噪聲還會使司乘人員感到疲勞,進而影響列車運行的安全性[3-4]。高速列車噪聲源可以概括為氣動噪聲、輪軌噪聲與牽引噪聲,所涉及范圍主要有車下設備噪聲、窗外透射噪聲、車體間連接氣動噪聲等[5-8]。當前高速列車減振降噪的措施主要通過列車內外地板間的多孔吸聲材料[9]、填充在側墻與頂板結構中的吸聲材料[10-11]等,鐵路沿線主要通過設置聲屏障實現減振降噪,降低列車對環境及周邊居民的影響。但由于高速列車噪聲主要為寬頻噪聲[12],噪聲源分離難度大[13]。另外,由于高速列車設計輕量化的需求,車體中可利用空間有限,因此研究新型降噪措施對乘員及鐵路沿線周邊環境具有十分重要的意義。聲子晶體及聲學超材料[14]近年來憑借其較為獨特的性質成為減振降噪領域的研究熱點,其主要機理為局域共振機理[15-16],作為周期性合成結構或材料,其組成成分可以為固體[17-18],也可為固-流組合[19]。依托其特有的“聲子帶隙”[20-21],可以使帶隙范圍內的聲波產生衰減,從而實現對噪聲的控制。研究表明,對于局域共振型聲子晶體,波速、散射體和基體材質、材料參數[22]、泊松比[23]等均會對聲子晶體能帶結構產生影響。
本文通過對比普通體心立方型聲子晶體與面心立方型聲子晶體,探索其各自適用范圍;分析面心立方中最具代表性的三維金剛石結構,研究改變散射體材料密度對帶隙結構的影響,并對其在軌道交通減振降噪領域進行展望。
1 結構類型選擇與計算
根據文獻[12]中針對高速動車組噪聲的研究,高速列車的噪聲頻率覆蓋在16 000 Hz以下,因此在結構選型對比中需要著重考慮其帶隙分布范圍。針對體心立方結構與面心立方結構進行建模,其三維三組元模型結構為基體、包裹層、散射體,相對應材料分別為環氧樹脂、橡膠、鉛。各種材料的基本參數如表1,能帶計算結果如圖1所示。
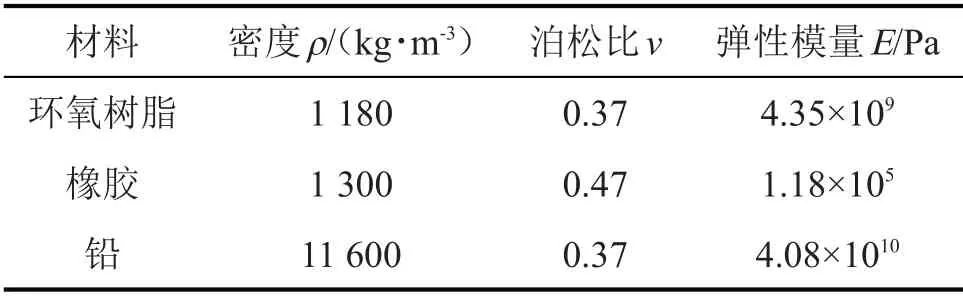
表1 各組分材料參數
將圖1中帶隙的相關參數整理如表2所示。
結合圖1 中的帶隙分布范圍以及表2 中的計算結果可知,面心立方結構帶隙分布范圍更貼近于軌道交通實際應用場景,而體心立方結構出現了第二帶隙,但由于其帶隙頻率分布范圍遠超出軌道交通領域的頻率范圍,因此在本研究中,應圍繞面心立方結構展開進一步研究。
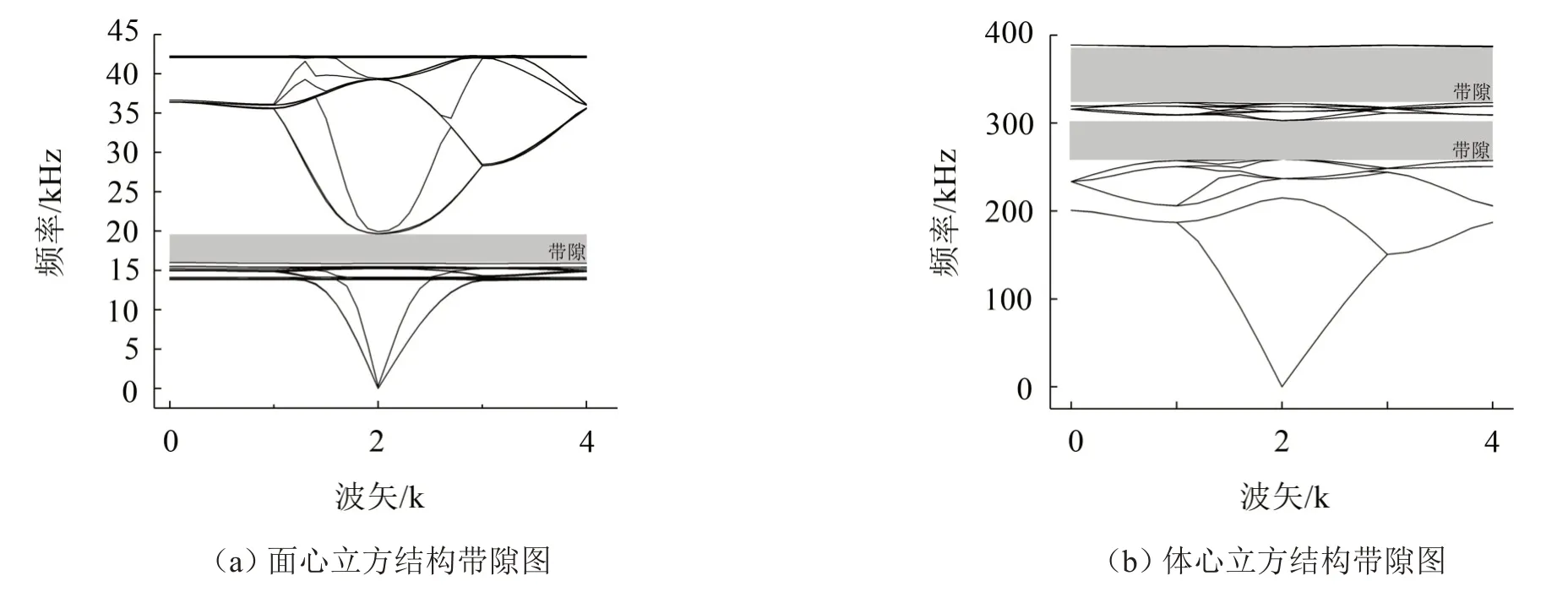
圖1 兩種結構帶隙圖

表2 兩種結構帶隙參數
針對面心立方結構中最典型的金剛石結構展開分析,在金剛石晶格原胞中,每個碳原子的四個價電子與最近的四個碳原子形成共價鍵,以五個碳原子為基準可構成正四面體結構,其中四個碳原子作為頂點,一個碳原子作為中心。金剛石結構聲子晶體模型示意圖如圖2所示,圖2(a)為結構的原胞圖,圖2(b)為結構擴展晶胞。
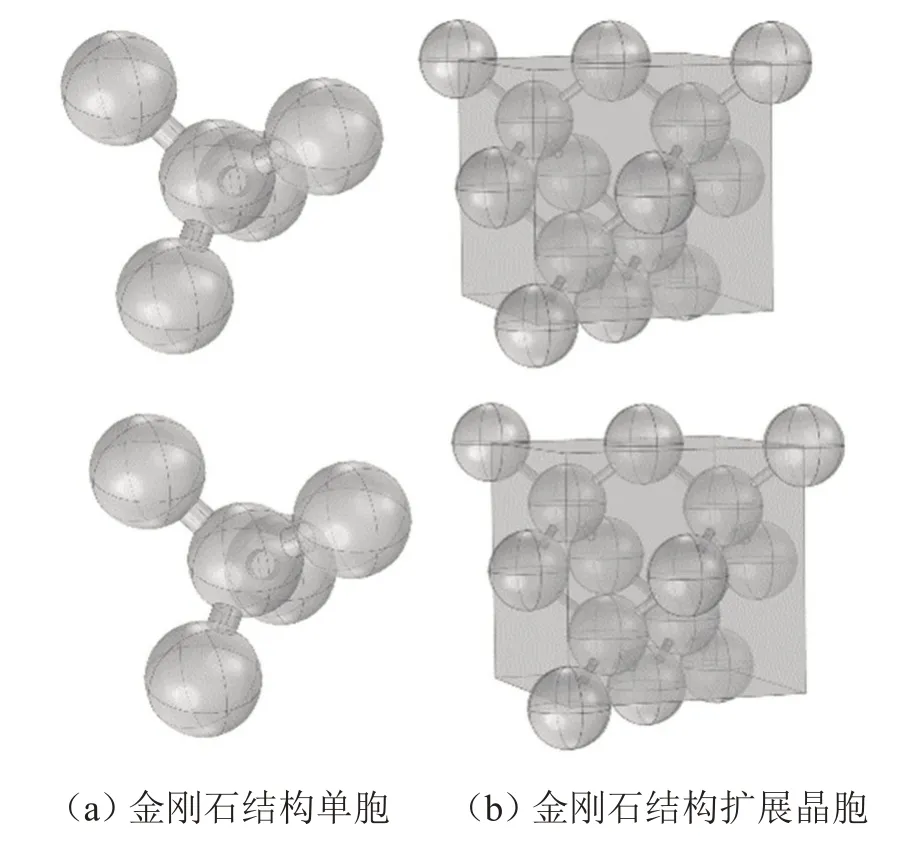
圖2 金剛石聲子晶體結構示意圖
所采用的有限元計算軟件COMSOL 主要借助聲學模塊對聲子晶體結構中的第一布里淵區進行掃描從而獲得聲子晶體的能帶結構。圖3所示為三維金剛石結構的第一布里淵區,其掃描路徑為U—L—Γ—X—W—K—U,即金剛石晶格結構的高對稱點。
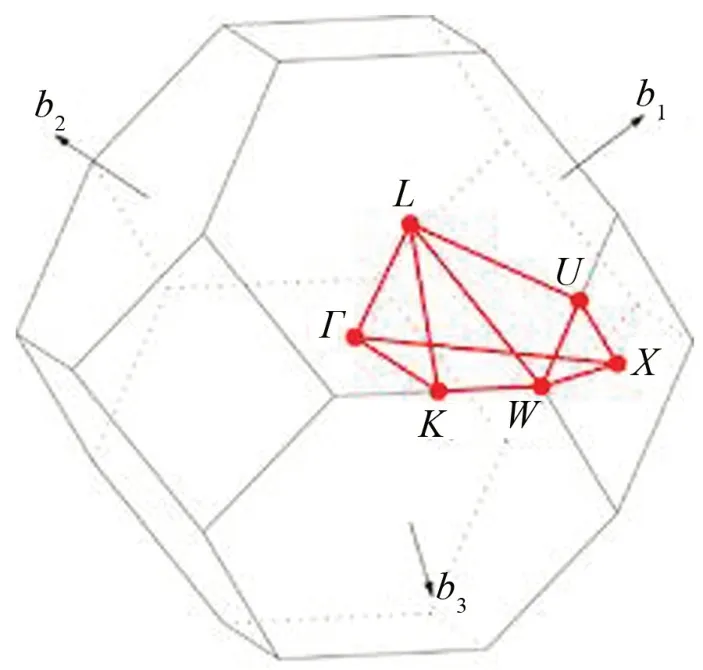
圖3 金剛石晶格聲子晶體第一布里淵區
2 正確性驗證
為了證明本次仿真計算方法以及結果的正確性,針對文獻[24]研究中的理論計算模型進行有限元模型仿真驗證。建立簡單立方型三維三組元聲子晶體結構,晶格常數為15.5 mm,其模型材料與材料參數如表3所示。
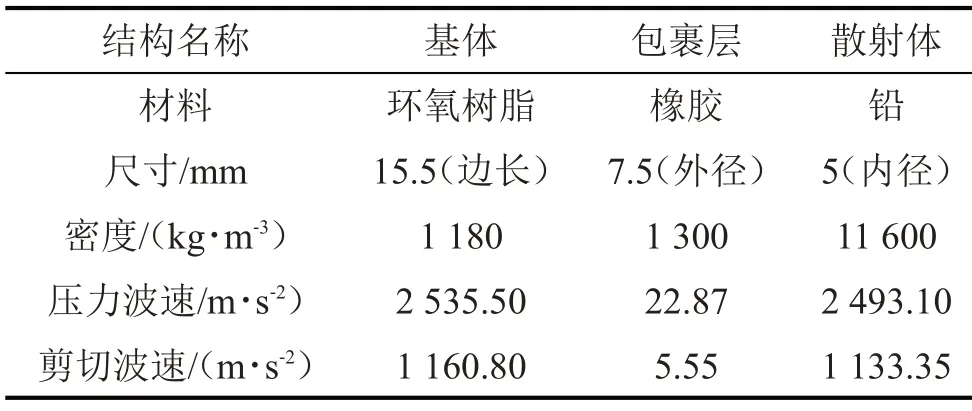
表3 簡單立方型聲子晶體結構材料參數
通過COMSOL Multiphysics 對此模型進行有限元仿真,將計算結果與文獻之中的結果進行對比。在文獻[24]計算中,簡單立方型聲子晶體在375 Hz~608 Hz范圍內存在帶隙,可以有效阻礙彈性波的傳遞。仿真結果中,簡單立方型聲子晶體的帶隙范圍在374.62 Hz~607.41 Hz,帶隙范圍誤差值為0.09%,說明本文采用的仿真以及高對稱點掃描方式,可以對三維三組元金剛石結構聲子晶體的能帶結構進行仿真計算,并且結果的準確性可以保證。圖4為本次仿真結果能帶結構圖。
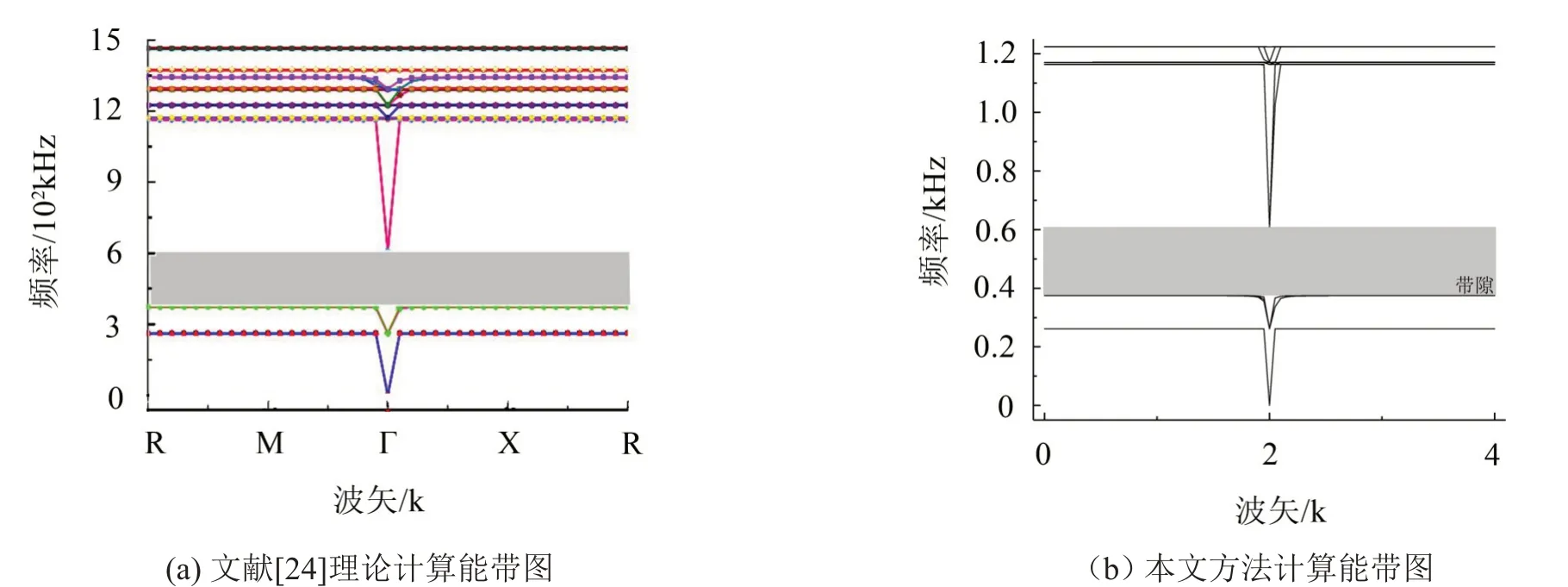
圖4 能帶結構對比圖
3 計算結果分析
三維金剛石結構的三種組元分別由三種材料構成,其中環氧樹脂作為基體材料,橡膠作為包裹層材料,鉛作為散射體材料。每種材料的主要參數如表1所示。
本文主要研究散射體密度對三維金剛石聲子晶體結構帶隙的影響,因此采用控制變量的方式針對三維金剛石聲子晶體中的散射體鉛的密度進行變量控制。以2 000 kg/m3為基準梯度,選取9組變量和1組鉛塊本身密度共10組數據進行仿真計算,散射體的密度取值如表4所示。

表4 散射體密度取值表
通過COMSOL Multiphysics 對此結構的第一布里淵區進行高對稱點參數化掃描,選取50個特征頻率進行數據分析,進而獲取各散射體密度下的帶隙結構圖。圖5 所示為部分密度梯度下的帶隙結構圖,其中圖5(d)為鉛本身密度參數下的帶隙結構圖。
從帶隙結構圖中可以看出,隨著散射體密度的增加,三維金剛石聲子晶體帶隙結構出現下移,帶隙上限值與下限值隨著密度的增加而降低。另外,圖5中的所有帶隙圖之中都存在數條近乎平直的能帶曲線,其波動幅值約為±0.5 Hz,僅占全局的0.001 4%,占比極小,可視為直線。
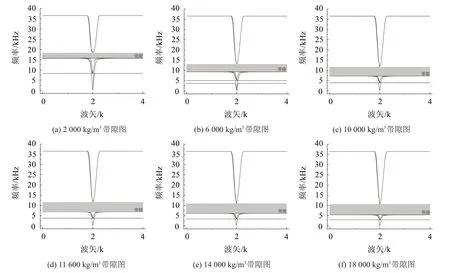
圖5 各密度梯度下三維金剛石聲子晶體能帶結構圖
將帶隙圖中的數據導出整理后得到不同密度取值下的帶隙參數。具體數值如表5所示。
圖6 為表5 數據導入至Origin 后繪制出來的曲線圖。
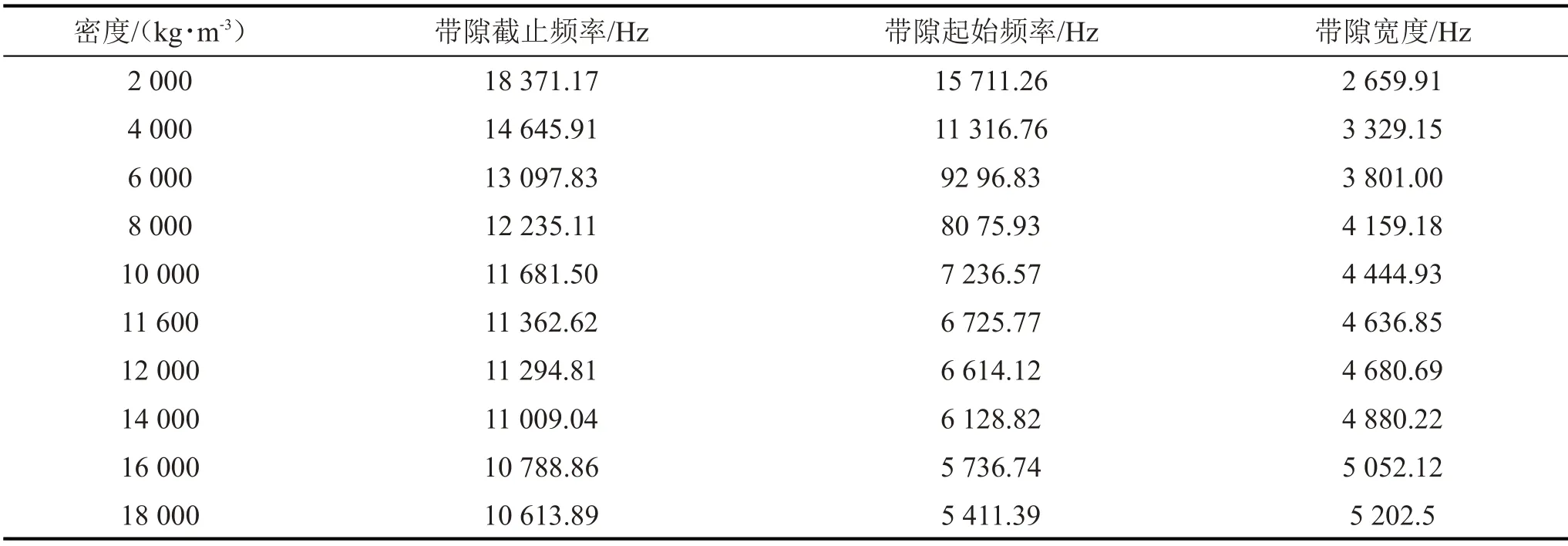
表5 不同密度取值下帶隙參數
由圖6可知,隨著密度的增加,三維金剛石聲子晶體的帶隙寬度逐漸增加,并且其帶隙起始頻率和帶隙終止頻率均從高頻開始降低。對圖6(a)中的數據進行2 階曲線、3 階曲線的擬合,計算得到兩種擬合方式的決定系數COD 值分別為0.995 和0.999,因此對于三維金剛石聲子晶體結構,其帶隙隨密度變化的結果更符合3 階曲線。根據圖6(b)可知,三維金剛石聲子晶體帶隙起始頻率、終止頻率隨著密度的增加,其下降趨勢逐漸緩和,斜率逐漸減小,斜率最大處為2 000 Hz~4 000 Hz處,可近似看作1階方程。在4 000 Hz 后,兩條曲線趨于平緩的趨勢出現明顯差別,帶隙終止頻率比帶隙起始頻率更快接近平緩,此即為帶隙寬度出現增加的原因。
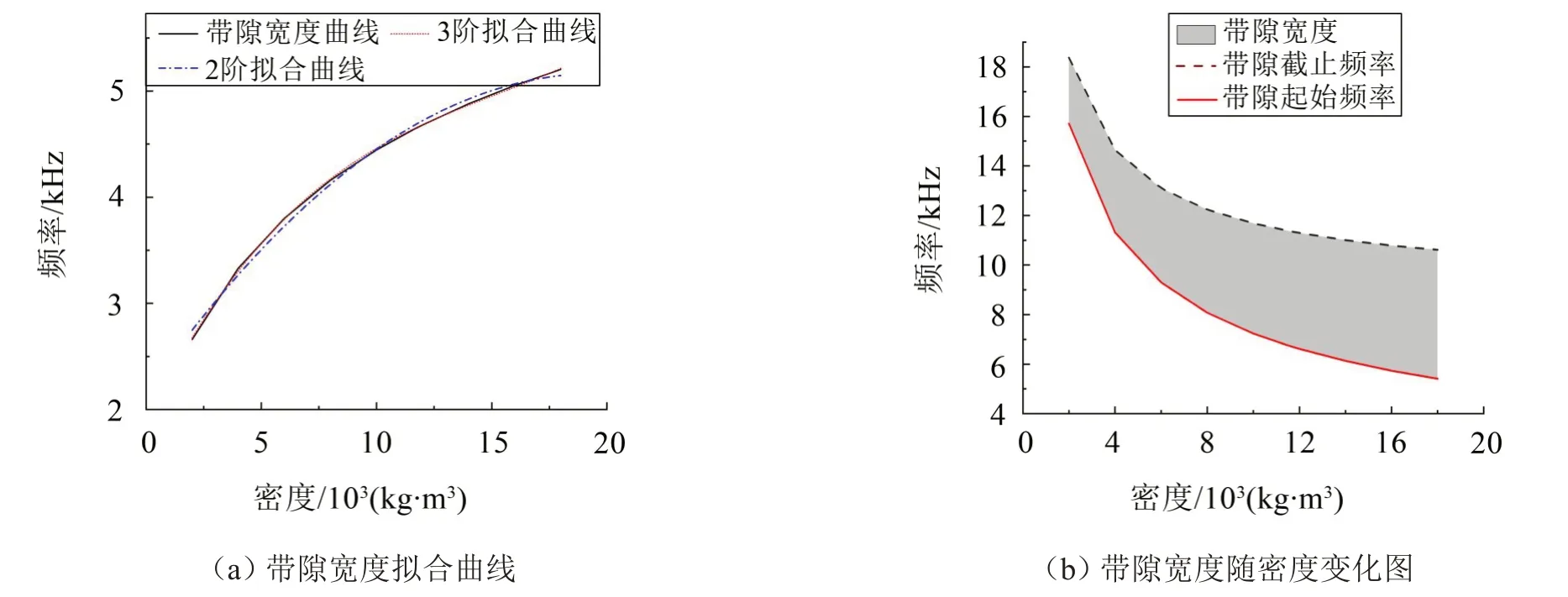
圖6 密度對帶隙的影響圖
4 結語
(1)提出了一種可應用于軌道交通領域的三維金剛石結構聲學超材料,仿真計算可得其有效作用頻率范圍在5 736.74 Hz~10 788.86 Hz之間,可以將在此頻率范圍之內的高速列車噪聲基本隔絕;
(2)在所計算模型之中,面心立方結構相較體心立方結構,其帶隙分布范圍更貼近于軌道交通真實應用場景。
(3)三維金剛石聲子晶體存在寬頻帶隙,并且其帶隙寬度與散射體密度之間構成3 階函數關系,但是當密度到達一定范圍后,密度對帶隙寬度的影響開始變小,帶隙產生變化的主導因素開始朝向其他材料偏移;
(4)隨著散射體密度的增加,三維金剛石聲子晶體結構的能帶結構朝低頻方向發展。同樣,在密度到達一定值時,密度不再作為主導因素,這一點可通過帶隙寬度隨密度變化圖中兩條曲線的斜率得知。
5 展望
(1)對比簡單的面心立方結構與三維金剛石結構可知,結構的調整會對帶隙產生影響,因此可利用此特點進行結構進一步優化調整;
(2)體心立方結構在本次計算中打開了第二帶隙,根據面心立方調整結構可調整帶隙結構可知,體心立方結構第二帶隙可通過調整其結構,可用于更加復雜的環境之中,如飛機翼板、高精度儀器減振之中;
(3)本研究中基于面心立方結構的擴展結構可應用于高速鐵路沿線聲屏障,以及高速列車地板填充層。

