基于多滑模變結構的雙向并網變換器虛擬慣性控制策略

劉彥呈，呂旭，張勤進，胡王寶，張瀚文

(大連海事大學輪機工程學院,遼寧省 大連市 116026)

0 引言

為應對日益嚴峻的化石能源枯竭和環境污染問題,以新能源發電為主的分布式發電技術得到了廣泛關注[1-3]。 光伏、蓄電池等直流電源的大規模接入及負荷側對直流功率需求的與日俱增促進了直流微電網的迅速發展[4-10]。 但直流微電網作為以電力電子變換器為主導的低慣性系統,當網內出現由光伏、風電等間歇性電源輸出功率波動及負載頻繁投切造成的擾動時,母線電壓會遭受到較大沖擊而劇烈波動,危害直流微電網的穩定運行[11-13]。

雙向并網變換器(bidirectional grid-connected converter, BGC)是連接直流微網與大電網的并網控制端口,在維持直流微網與大電網間能量的雙向流動, 穩定直流母線電壓等方面承擔關鍵作用[14-15]。

針對直流微網慣性低、母線電壓抗干擾能力差的問題,文獻[16]通過類比交流微網中的虛擬同步發電機控制提出一種應用于直流微網雙向并網變換器的虛擬慣性控制策略。 通過在傳統電壓環外加入虛擬慣性方程,在變換器直流側模擬電容的穩壓特性,從而增強直流微網的慣性,抑制直流母線電壓波動。

然而,虛擬電容的引入會降低系統的動態響應速度,導致暫態下直流母線電壓的恢復時間變長。文獻[17]通過建立直流電壓變化率與虛擬電容之間的函數關系,提出靈活虛擬慣性控制策略。 然而,僅通過調節虛擬電容值對系統動態性能的改善作用有限,且虛擬電容的頻繁切換可能會導致母線電壓振蕩。

目前,大量關于BGC 虛擬慣性控制(virtual inertia control, VIC)策略的研究,在閉環控制中仍采用傳統的比例積分(proportion integration,PI)控制,然而PI 控制很難使非線性系統獲得較好的動態性能。 因此,為改善功率擾動下母線電壓的動態性能,有學者提出將非線性控制算法引入到虛擬慣性控制策略中。 文獻[18] 提出一種基于無源控制(passivity-based control, PBC)的虛擬慣性控制策略,從能量角度出發設計了基于歐拉-拉格朗日(Euler-Lagrange, EL)模型的電流內環無源控制器,通過調節注入的阻尼大小使網側電流收斂到給定值。 該方法減小了直流電壓波動,但系統調節時間較長。 由于無源控制對系統模型和參數的依賴度高,導致受擾下系統很難獲得良好的跟蹤效果。

滑模變結構控制[19-21](sliding mode control,SMC)因系統在進入滑模運動后不受系統參數變化及外界擾動的影響而具有較強的魯棒性,且其具有控制算法簡單、動態響應速度快等優點,將其引入BGC的虛擬慣性控制中可以有效改善系統的動態特性,增強直流母線電壓的抗擾能力。 文獻[22]將多滑模控制算法引入三相脈寬調制(pulse width modulation,PWM)整流器中,改善了直流電壓波動和響應速度,但電流環引入滑模算法產生的抖振問題使并網電流諧波較大。 文獻[23]提出一種基于多滑模變結構的網側整流器控制策略,設計了電壓滑模面和電流滑模控制律。 為削弱滑模抖振,采用基于指數趨近律的滑模電流控制,在提高直流電壓動態特性的同時保證了網側電流諧波畸變率低。

因此,為改善直流母線電壓的動態性能,同時增強直流微網的慣性,本文提出一種基于多滑模變結構的雙向并網變換器虛擬慣性控制策略。 內環采用基于指數趨近律的滑模電流控制,快速跟蹤并網電流給定值;外環建立虛擬慣性方程與電壓滑模面結構,增強直流母線電壓的穩定性。 通過小信號建模分析BGC 系統在本文所提控制方法下的穩定性,并給出虛擬慣量的選取范圍。 最后,通過仿真和實驗驗證所提控制策略的有效性。

1 含BGC 接口的直流微電網結構

圖1 為含BGC 接口的直流微電網拓撲結構圖,該直流微電網主要由雙向并網變換器、分布式電源、儲能裝置、負載以及相應的功率變換器組成。 當直流微電網運行于并網模式時,BGC 采用直流側恒壓控制,平衡直流微電網內的功率盈缺,穩定直流母線電壓。 當交流電網出現故障時,直流微電網切換到孤島模式,BGC 退出運行,直流微電網的母線電壓由儲能裝置進行維持。

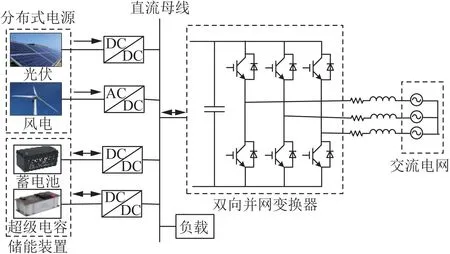
圖1 含BGC 的直流微電網結構圖Fig.1 Diagram of DC micro-grid with BGC

本文為著重分析并網模式下BGC 的控制策略,將BGC 直流側的分布式電源、儲能及相應的功率變換器等效為功率源Pcs,負載側接入恒功率負載(constant power load, CPL)。 簡化后的含BGC 的直流微電網等效結構如圖2 所示。 圖2 中,Q1—Q6分別為BGC 主電路三相橋臂的6 個絕緣柵雙極型晶體管(insulated gate bipolar transistor,IGBT) 開關管。um(m=a,b,c)為三相電網電壓,im為三相并網電流;em為BGC 交流側端電壓,udc為BGC 直流側母線電壓;idc為橋臂直流側輸出電流;i0為BGC 直流側輸出電流,iR為直流側負載電流。L和R分別為交流側濾波電感和電阻,C為直流側穩壓電容。 為維持直流微網內電源和負載的功率平衡,BGC 會根據差額功率傳輸方向的變化在整流和逆變工作狀態間自主切換,以保證直流母線電壓恒定。

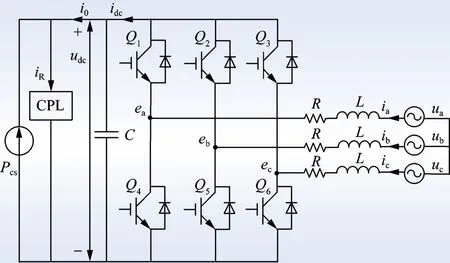
圖2 含BGC 的直流微電網等效結構圖Fig.2 Equivalent diagram of DC micro-grid with BGC

2 基于多滑模變結構的BGC 虛擬慣性控制

2.1 電壓外環滑模控制器設計

假設BGC 主電路功率開關器件均為理想開關,開關頻率遠高于電網的基波頻率。 交流電網等效為理想三相電壓源,網側濾波電感三相平衡,根據圖2,基于等值變換建立BGC 系統在同步旋轉dq坐標系下的數學模型:

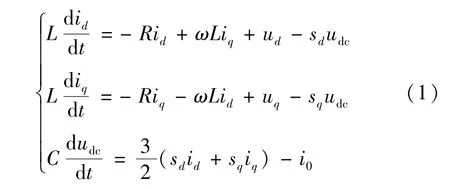
式中:ud和uq分別為三相電網電壓ua、ub和uc在dq軸的電壓分量;id和iq分別為三相電網電流ia、ib和ic在dq軸的電流分量;sd和sq分別為開關函數在dq軸的分量;ω為交流電網的角頻率。

由式(1)可知BGC 系統有sd和sq兩個控制量,其中sd用于控制直流側電壓udc,sq用于控制無功電流分量iq。 以udc和iq作為輸出變量,分別選取其跟蹤誤差σu和σq作為系統的狀態變量,設計電壓外環滑模控制器,滑模面函數S(·)為:

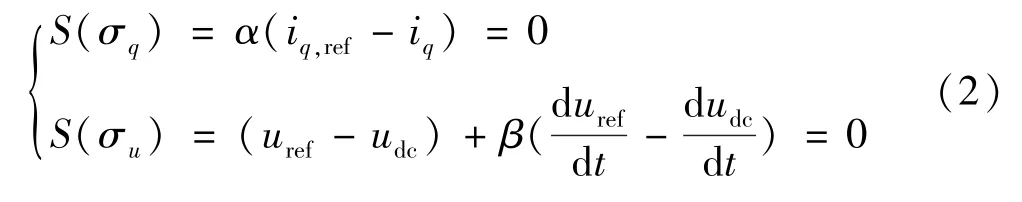
式中:α、β為電壓滑模面參數;iq,ref為網側無功電流的給定值;uref為直流側電壓的給定值。

將式(1)代入到式(2)中得:

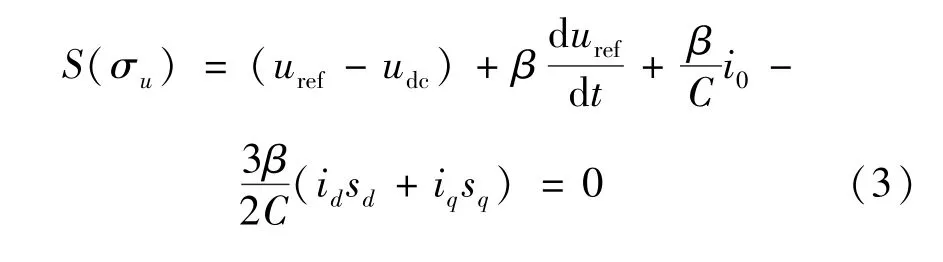
將式(3)改寫為:

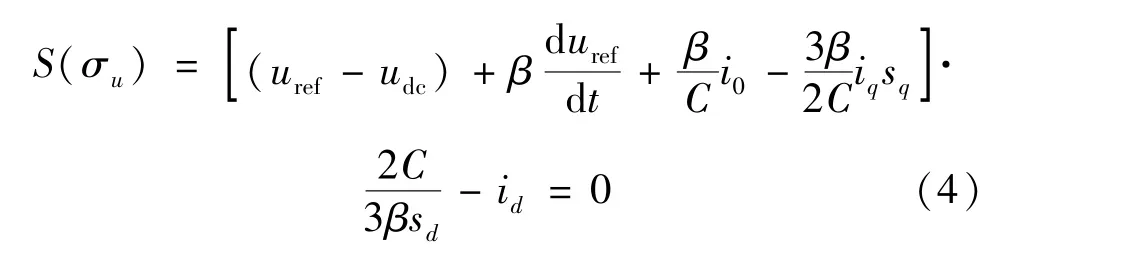
在BGC 系統中,考慮網側電壓三相平衡,BGC以單位功率因數運行,則穩態條件下,對式(1)中的控制量進行化簡:

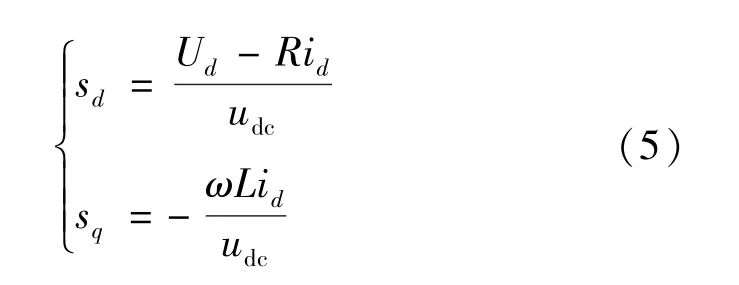
式中:Ud為電網電壓在d軸的穩態分量。

將式(5)代入式(4)化簡得到:

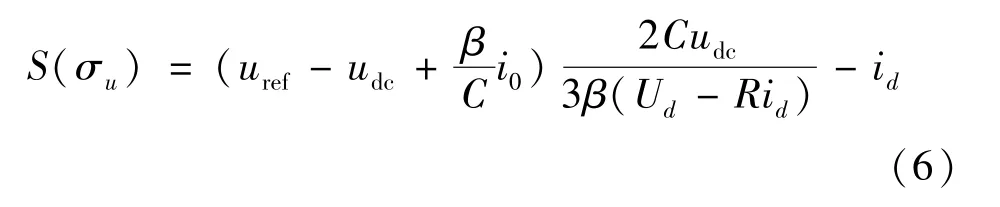
由此,得到電壓外環的滑模控制方程,電壓外環的輸出作為內環電流有功分量的給定值,即:

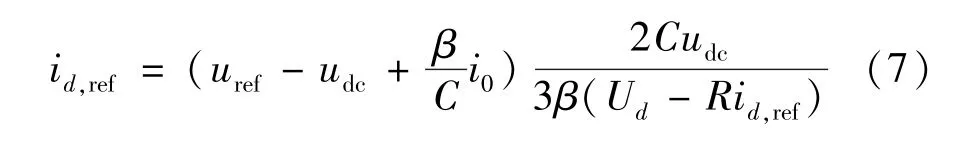
式中:id,ref為網側d軸有功電流分量的給定值;β為電壓滑模面的偏差放大系數。 有研究表明[24]偏差放大系數的確定要考慮開關的死區和延時,其值不能過大,一般取值為0.01 ～0.10,經仿真調試,本文β取值為0.05。

2.2 電流內環滑模控制器設計

電流內環滑模控制器的控制目標為:通過控制變量sd和sq,使dq軸電流分量id和iq跟隨電流給定值id,ref和iq,ref,令iq,ref=0,實現單位功率因數控制。 分別以網側電流dq分量的跟蹤誤差σd和σq作為狀態變量設計滑模面函數S(·):

為抑制因滑模控制律的不連續導致的抖振,改善滑模到達段的運動,采用指數趨近律來設計電流內環滑模控制律,即:

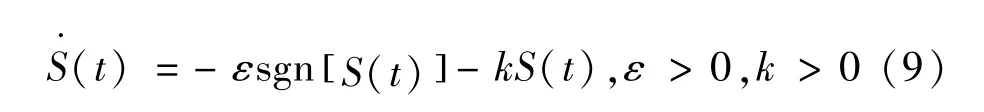
式中:ε為系統運動點趨近滑模面的速度,選取較小的ε值使系統狀態距離滑模面較近時降低趨近速度,避免狀態軌跡到達滑模面后產生強烈的抖振;k為指數趨近項系數,選取較大的k值使系統狀態在距離滑模面較遠時快速趨近滑模面。 本文綜合考慮內環響應速度及滑模抖振的影響,在保證系統穩定約束條件下電流滑模控制的參數選取范圍為:100 ＜k＜1000,0 ＜ε＜100。 經仿真調試后,本文選取動態性能較佳的一組參數:kd=kq=500,εd=εq=100。 其中εd和εq,kd和kq分別為dq軸內環電流滑模控制器的相關參數。

結合式(1)、式(9),對內環電流進行前饋解耦,得到電流內環的滑模控制方程:

對式(8)求導,并聯立式(1)、式(10)可得:

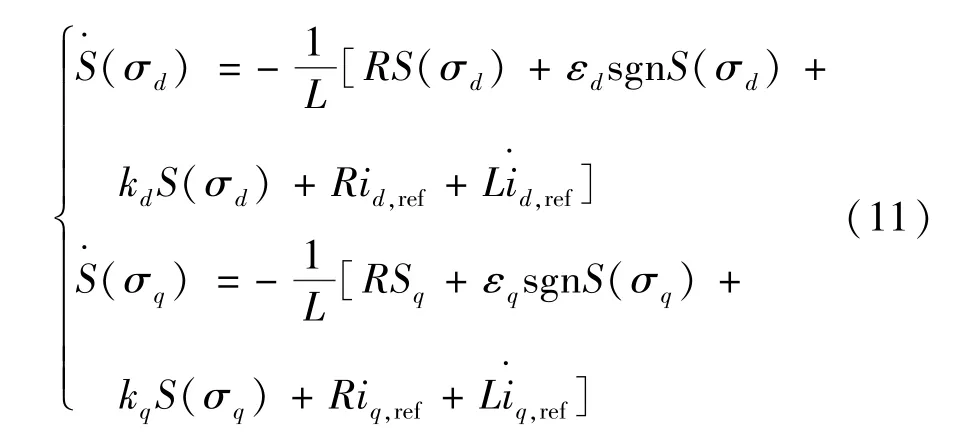
為確保滑模控制算法的可達性及穩定性,需滿足以下條件:

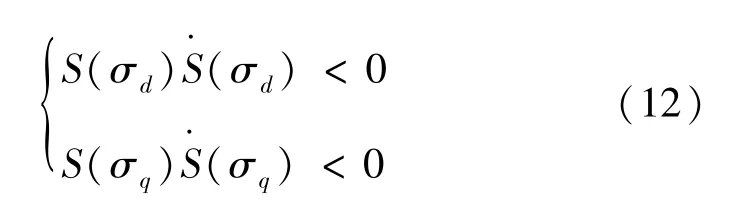
將式(8)、式(11)代入式(12)得:

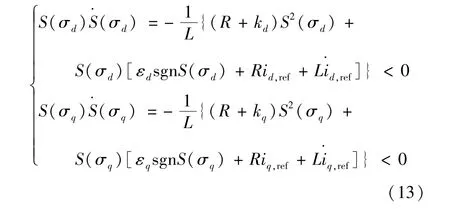
可推導出滿足式(13)的滑模控制參數:

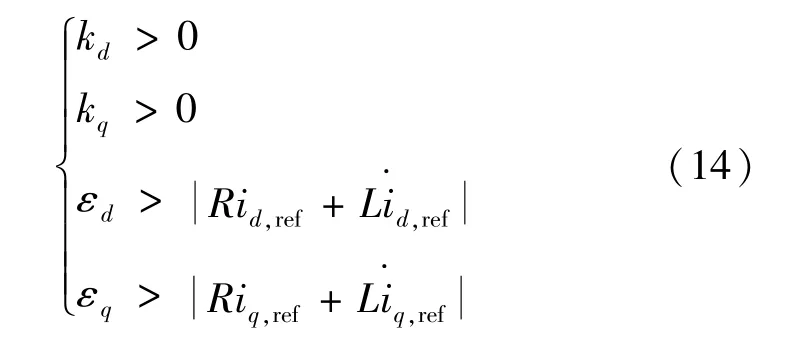
上述控制參數同時滿足式(15)給出的李雅普諾夫函數V是非正定的,即證明滑模控制系統趨于穩定。

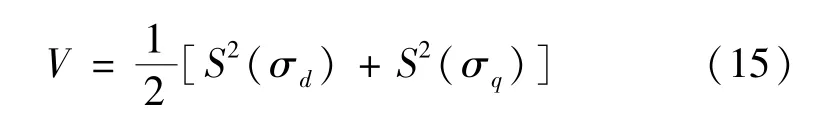
2.3 BGC 虛擬慣性控制策略

交流微網中的VSG 控制策略基于有功-頻率下垂控制使逆變器模擬出同步發電機的旋轉慣性及阻尼特性,當電網頻率突變時,虛擬慣量J的引入使VSG 輸出的有功功率得到快速調節,從而使逆變器對電網頻率具有一定的慣性支撐,有效抑制了電網頻率的大幅波動。 VSG 的有功-頻率下垂方程為:

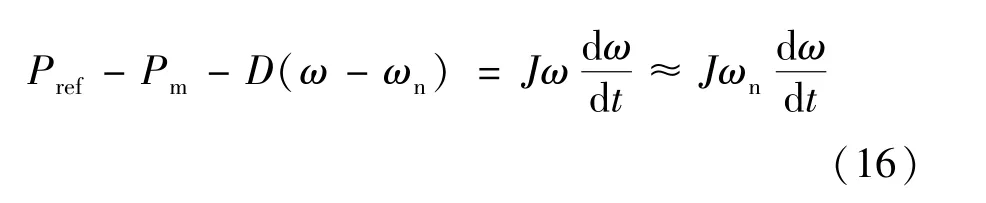
式中:Pref和Pm分別為給定有功功率和VSG 輸出有功功率;ωn為交流電網額定角頻率;J和D分別為VSG 控制中的虛擬轉動慣量和頻率阻尼系數。

根據文獻[16]給出的類比VSG 控制的直流微網虛擬慣性控制策略,交流微網中的角頻率、有功功率及虛擬轉動慣量與直流微網中的直流母線電壓、直流側輸出電流及直流側虛擬電容存在對應關系。 據此,本文采用的虛擬慣性控制方程為:

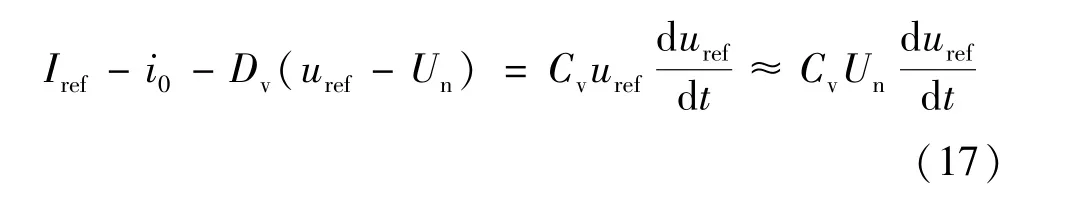
式中:Iref為BGC 輸出電流給定值;Dv為電壓阻尼系數;Un為直流側電壓額定值;uref為虛擬慣性環節輸出的直流電壓參考值;Cv為虛擬電容值。

通過式(17)可知,當直流微網內功率波動導致直流母線電壓突變時,通過虛擬電容Cv迅速調節BGC 直流側輸出電流,從而增強直流微網的慣性。理論上,Cv值越大,直流微網的慣性越強。

因此,結合式(7)、式(10)和式(17)給出的控制方程,建立引入多滑模變結構的VIC 策略的BGC 系統控制框圖,如圖3 所示。

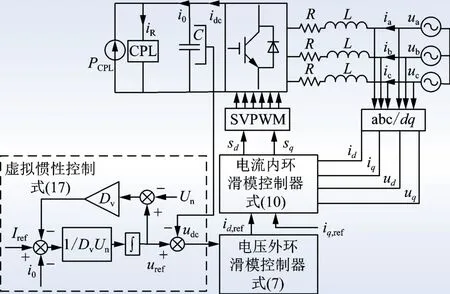
圖3 BGC 系統控制框圖Fig.3 Block diagram of BGC system control

3 小信號穩定性分析

為進一步分析引入多滑模控制算法的虛擬慣性控制策略對BGC 系統影響,建立所提控制策略下BGC 的小信號模型并分析系統的穩定性。

首先建立電流內環的小信號模型,考慮到d軸和q軸的電流環具有對稱性,為簡化分析,本文以d軸電流環為例。 設電流調節器的等效傳遞函數為Gi(s),得到電流內環的小信號方程:

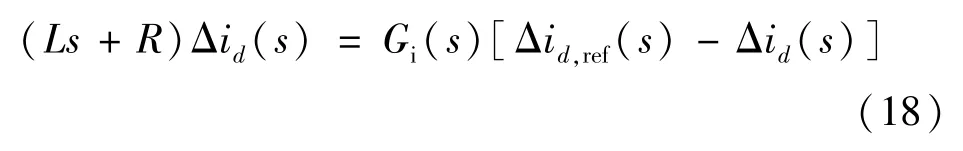
式中:s為拉普拉斯算子;Δid和Δid,ref分別為網側d軸電流和d軸電流給定值的小信號擾動量。

采用基于指數趨近律的內環滑模電流控制替換傳統內環PI 控制,即:

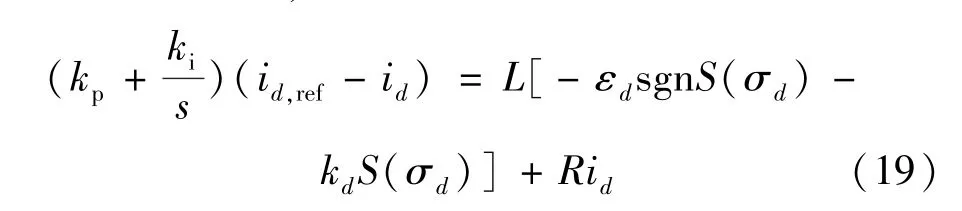
對式(19)右側分段線性化可得:

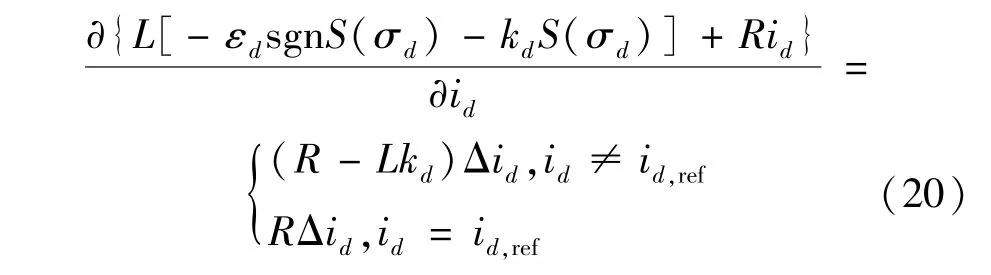
由式(20)可知,滑模電流控制對系統小信號擾動的穩定性可等效為內環PI 控制環節中ki=0,kp取值為(R-Lkd)或R時的穩定性。 與PI 控制相比,滑模電流控制減少了積分環節,在避免了內環積分系數較小引起不穩定影響的同時,提高了內環的響應速度。 因此,滑模電流控制的等效傳遞函數Gi(s)可表示為:

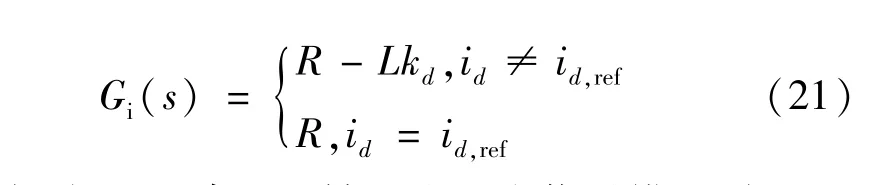
根據式(18)建立d軸電流環小信號模型,如圖4所示,其中Kpwm為橋路PWM 等效增益。

圖4 d 軸電流環小信號模型Fig.4 Small-signal model of d-axis current

下面建立滑模電壓外環的等效傳遞函數Gv(s),并推導引入虛擬慣性控制環節的BGC 系統的小信號模型。

根據式(7)所給出的電壓滑模方程,將式中的狀態變量寫成穩態量和小信號擾動量之和,即uref=Uref+Δuref,udc=Udc+Δudc,忽略電流擾動項Δi0和二次擾動項,根據疊加原理可得:

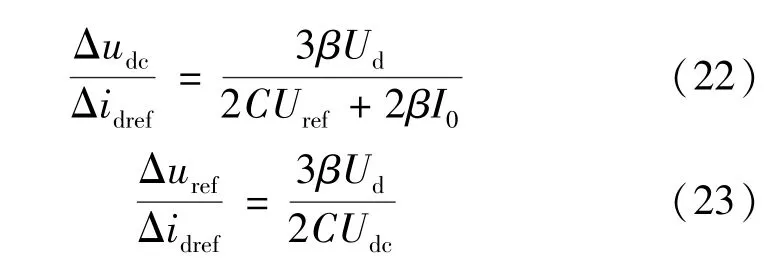
式中:Δudc和Δuref分別為BGC 直流側母線電壓和母線電壓給定值的小信號擾動量;Udc為BGC 直流側母線電壓的穩態值。

由此可推導出滑模電壓控制的等效傳遞函數:

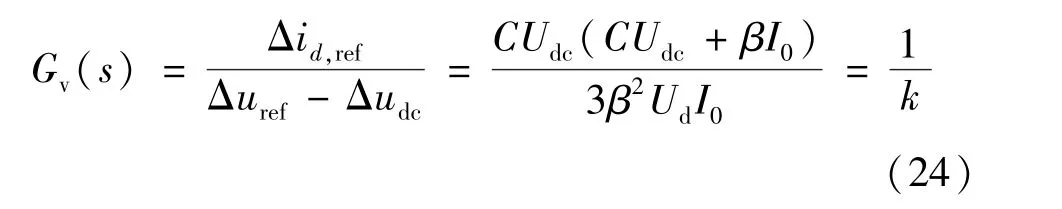
由式(24)可知滑模電壓控制的傳遞函數可等效為線性比例控制環節,式中k為比例常數。

設定BGC 運行于單位功率因數,即無功電流分量iq=0,根據BGC 交、直流側功率平衡有:

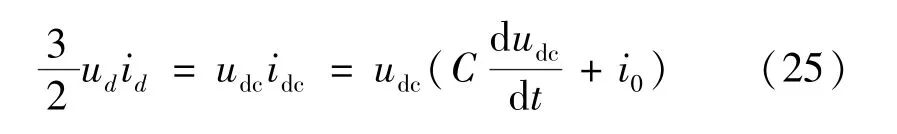
將式(25)中的狀態變量改寫為穩態量與小信號擾動量之和,即i0=I0+Δi0,udc=Udc+Δudc,忽略電網電壓擾動項Δud和二次擾動項,式(25)小信號方程為:

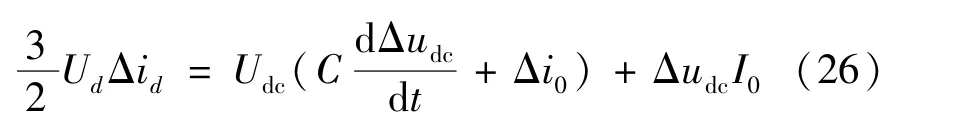
式中:Δi0和I0分別為BGC 直流側輸出電流i0的小信號擾動量和穩態值。

根據疊加原理,對式(26)進行拉普拉斯變換可得:

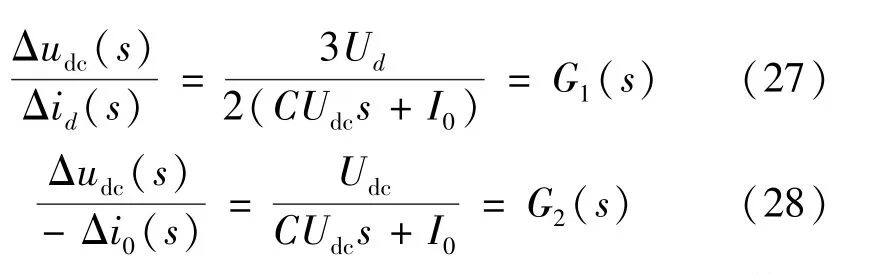
對式(18)給出的虛擬慣性控制方程進行小信號分析得:

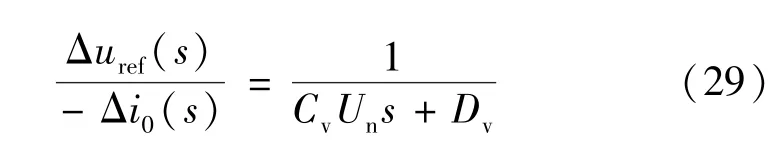
據此,建立BGC 系統的小信號模型如圖5 所示。

圖5 BGC 系統的小信號模型Fig.5 Small-signal model of BGC system

根據圖5,推導BGC 系統閉環傳遞函數G(s):

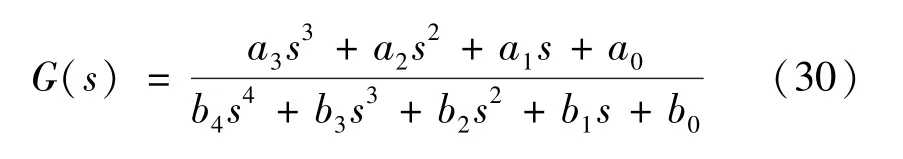
其中,

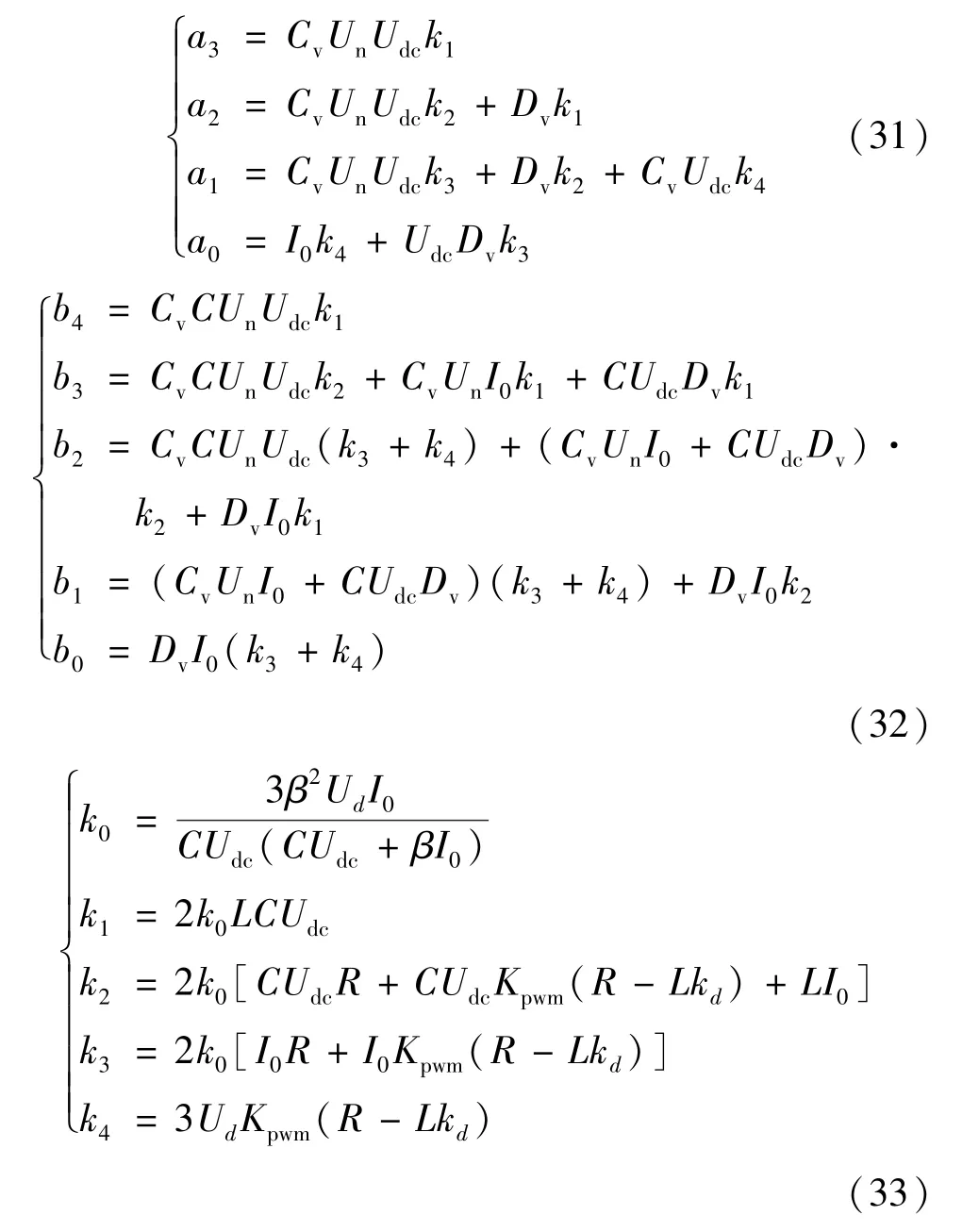
為分析所提控制策略下系統的穩定性,根據式(30)繪制出BGC 閉環控制系統的Nyquist 曲線,如圖6 所示。 其中,圖6(a)為不同虛擬電容Cv下系統的Nyquist 曲線圖,圖6(b)為不同阻尼系數Dv下系統的Nyquist 曲線圖。

從圖6 中可以看出在多滑模控制算法下BGC 系統的Nyquist 曲線不包圍( -1,0)點且距其有較遠的距離,系統維持穩定。 且當虛擬慣量Cv和Dv在一定范圍內變化時,系統仍具有良好的穩定性。

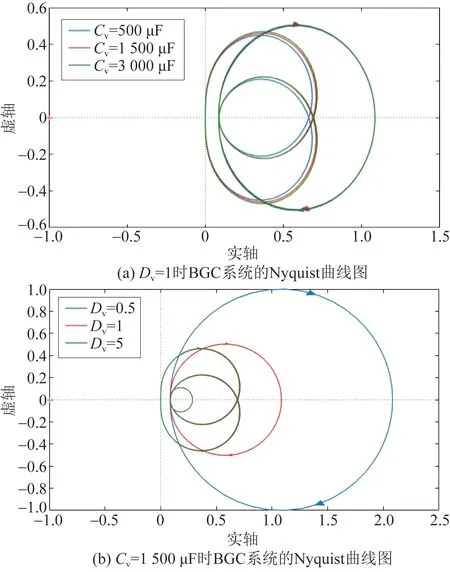
圖6 BGC 系統的Nyquist 曲線圖Fig.6 Nyquist curve of BGC system

4 仿真分析

為驗證所提控制策略的有效性,在Simulink 中搭建了圖2 所示的BGC 系統仿真模型,系統仿真參數見表1。 本文在PI 參數選取上參照典型二階系統的整定方法,通過仿真調試綜合考慮比例及積分系數對暫態波動及恢復速度的影響,選取動態性能較佳的一組參數。 無源控制注入阻尼參數的選取同樣存在波動幅值與響應速度的矛盾,注入阻尼較小時,電壓波動大但響應速度快;注入阻尼較大時,電壓波動小但響應速度慢。 因此,經仿真調試,無源阻尼參數也遵循動態性能較佳這一選取原則。

表1 BGC 系統仿真參數Table 1 Simulation parameters of BGC system

將本文所提基于多滑模控制的VIC 策略與基于PI 控制、無源控制的VIC 策略進行仿真對比,三種控制策略下BGC 直流側母線電壓的動態響應和網側電流的電能質量分析如圖7 和圖8 所示。 設定BGC 工作在整流狀態下傳輸功率P為正值,逆變狀態下傳輸功率P為負值,給出如下2 種案例。

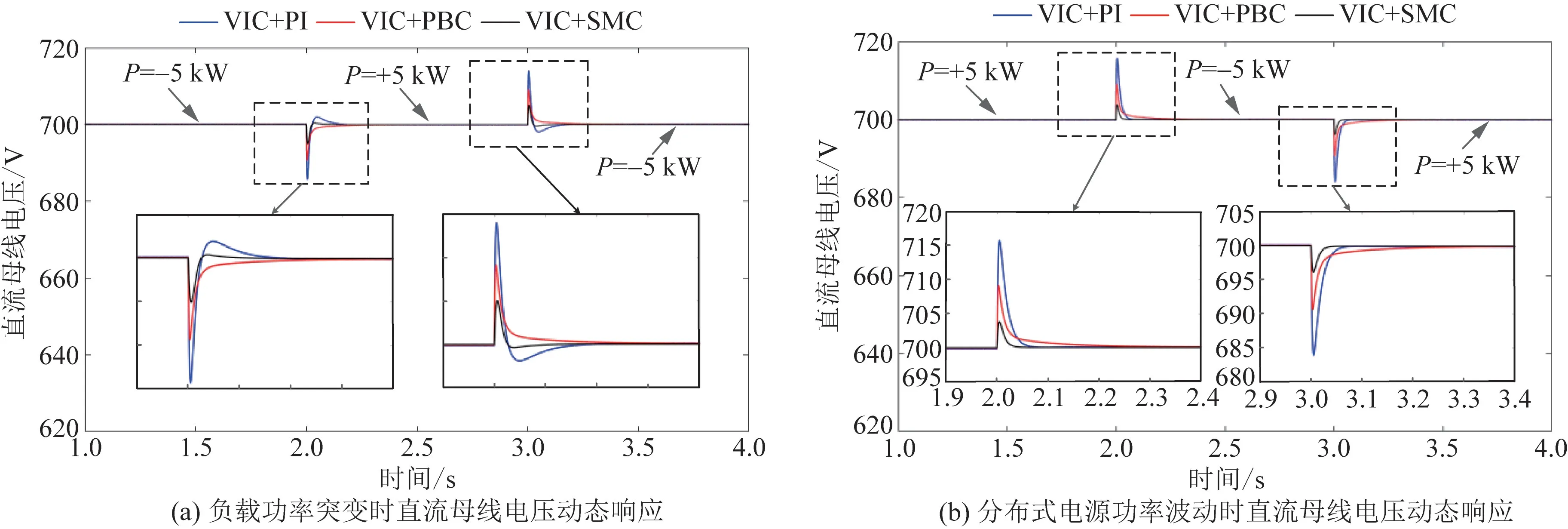
圖7 三種控制策略下直流母線電壓對比Fig.7 Comparison of DC bus voltage under three control strategies

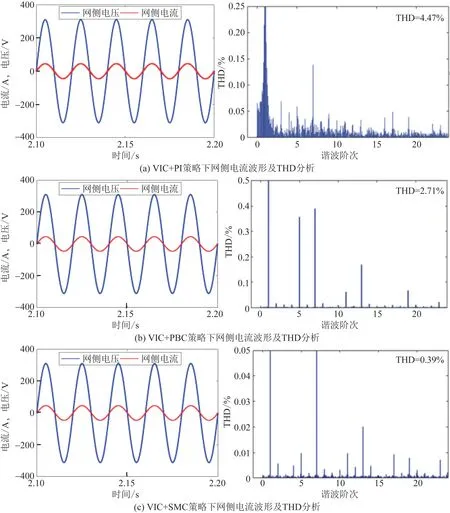
圖8 三種控制策略下網側電流波形及THD 分析Fig.8 Waveforms of grid-connected current and THD analysis under three control strategies

仿真案例1:研究恒功率負載功率突變對直流母線電壓的影響。 直流側分布式電源輸出額定功率為15 kW,2.0 s 時負載功率由初始功率10 kW 突增為20 kW,3.0 s 時負載功率又突減為10 kW。

仿真案例2:研究分布式電源功率波動對直流母線電壓的影響。 設定恒功率負載額定功率為20 kW,分布式電源輸出功率在2.0 s 時由初始功率15 kW突增為25 kW,在3.0 s 時又突減為15 kW。

表2 給出的三種BGC 控制策略分別為基于PI控制的虛擬慣性控制(virtual inertia control, VIC),基于無源控制(passivity-based control, PBC)的虛擬慣性控制,以及本文所提出的基于多滑模變結構控制(sliding mode control, SMC)的虛擬慣性控制策略。

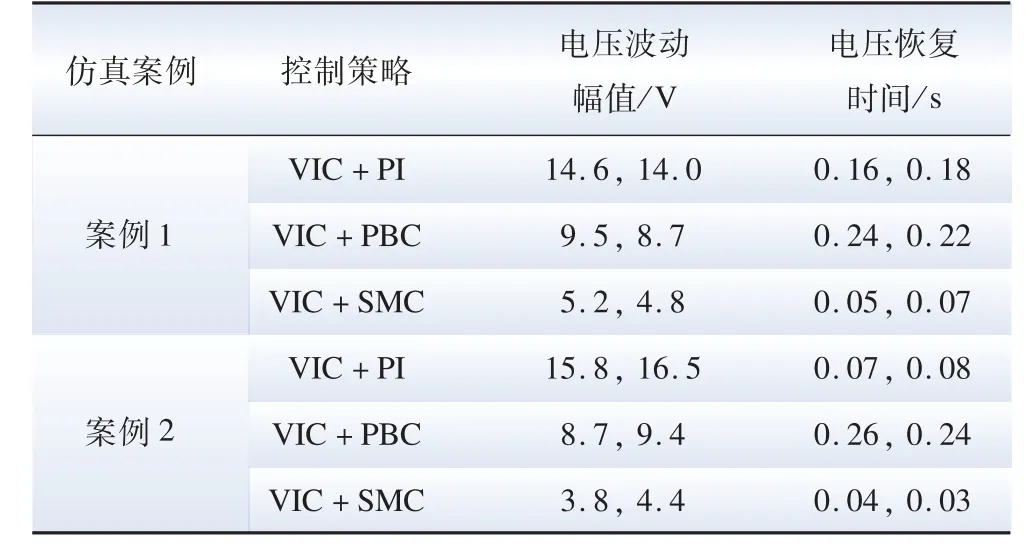
表2 三種控制策略下直流母線電壓動態性能指標Table 2 Transient performance index of DC bus voltage under three control strategies

由圖7 及表2 的數據可知,經不同仿真案例分析對比,采用基于多滑模變結構的VIC 策略與基于PI控制、無源控制的VIC 策略相比,直流母線電壓暫態波動的幅值最小,同時母線電壓恢復到穩態所需時間也最短,在三種控制策略中動態性能最優。

由圖8 可知,三種控制策略均實現了網側電壓、電流單位功率因數控制這一目標。 根據總諧波失真(total harmonic distortion,THD)分析可知,與PI控制和無源控制相比,多滑模變結構控制下網側電流總諧波畸變率更低,更好地保證了BGC 網側電能質量。

圖9 為在本文所提VIC +SMC 控制策略下設定不同虛擬電容Cv時直流母線電壓的動態響應對比。由圖9 可知,在BGC 虛擬慣性控制環節,隨著虛擬電容Cv的增大,母線電壓的暫態波動幅值逐漸減小,直流微網的慣性得到增強。 但較大的虛擬電容Cv會延長母線電壓恢復到穩態的時間,使系統的動態響應速度變慢。 因此需根據實際控制需求選取合適的虛擬電容值。

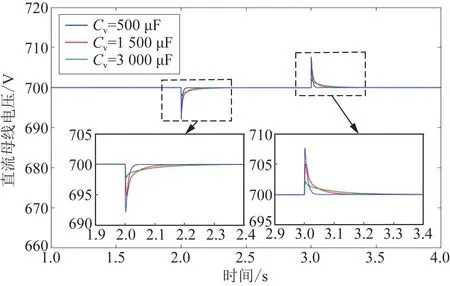
圖9 不同Cv下的直流母線電壓動態響應Fig.9 Dynamic response of DC bus voltage under different Cv

上述結果驗證了本文所提基于多滑模變結構的VIC 策略能夠在負載功率突變及分布式電源波動時有效抑制直流母線電壓大幅波動,增強直流微網的慣性,使BGC 系統具有較好的動、靜態性能。

5 實驗驗證

為進一步驗證本文所提控制策略的有效性,搭建的由StarSim HIL 控制的BGC 系統的硬件在環實驗平臺如圖10 所示,實驗參數與仿真相同。 圖11 給出了負載功率突變下采用基于PI 控制和多滑模控制的VIC 策略的直流母線電壓對比及不同虛擬電容下直流母線電壓的動態響應波形。

圖10 基于StarSim HIL 的BGC 系統實驗平臺Fig.10 Experimental platform of BGC system based on StarSim HIL

圖11(a)—(c)給出的電壓局部放大圖中,縱坐標每小格電壓值為2 V,橫坐標每小格時間間隔為40 ms。從圖中對比可以看出,本文提出的基于多滑模變結構(SMC)的VIC 策略與基于PI 控制的傳統VIC 策略相比,暫態下直流母線電壓的波動幅值更小,母線電壓恢復到穩態的時間更短,提高了BGC 的動態性能。 同時,選取不同的虛擬電容值,隨著Cv的增大,母線電壓波動幅值進一步減小,但同時會延緩系統的動態響應速度。

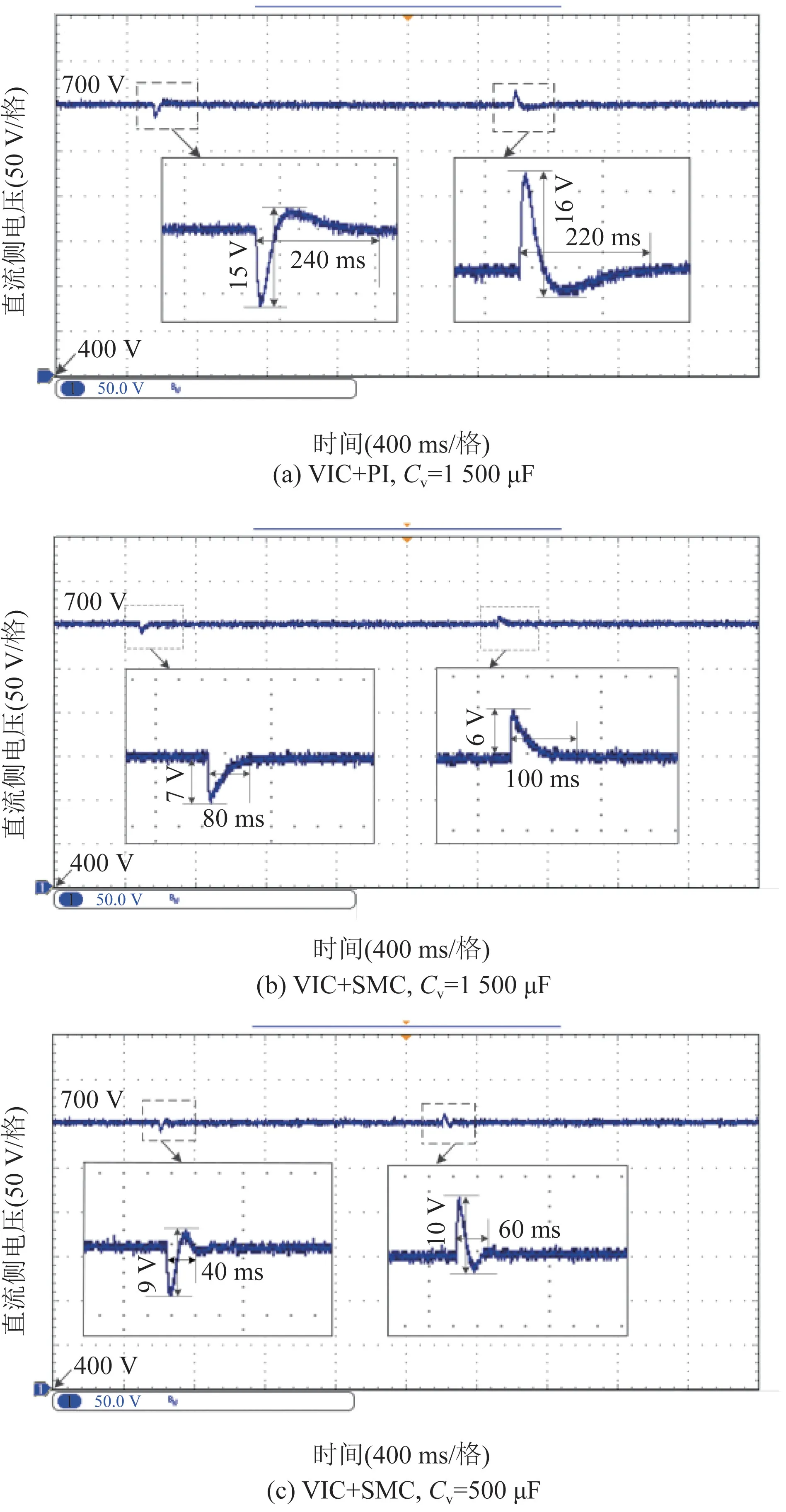
圖11 負載功率突變時直流母線電壓的實驗波形Fig.11 Experimental waveforms of DC bus voltage when load power suddenly changes

圖12 給出了采用基于PI 控制和多滑模控制的VIC 策略下BGC 的網側電壓和電流波形。 由圖12可知,本文所提控制策略與基于PI 控制的VIC 策略相比,并網電流總諧波畸變率更小, 更好地保證了BGC 交流側的電能質量。

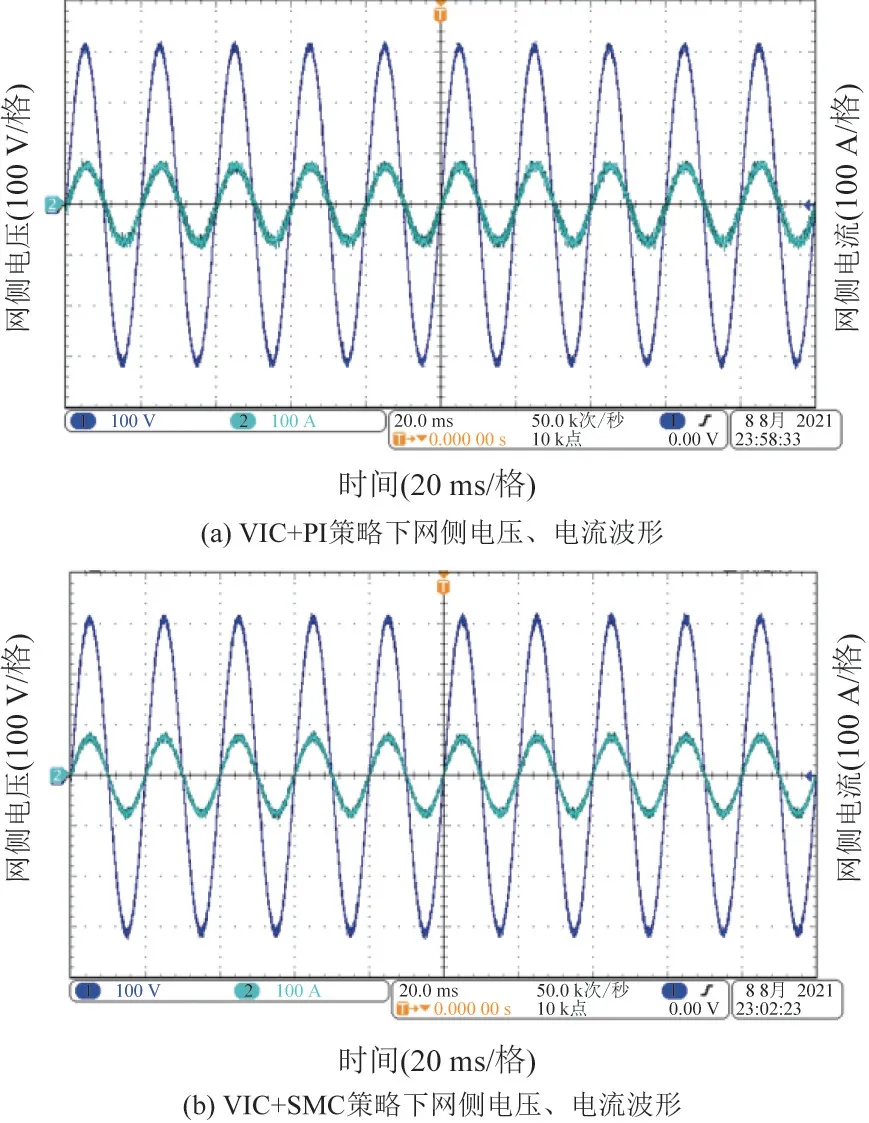
圖12 不同策略下網側電壓、電流的實驗波形Fig.12 Experimental waveforms of voltage and current at network side under different control strategies

6 結論

為提高暫態下BGC 的控制性能,抑制負載擾動下直流母線電壓的大幅波動,本文在傳統VIC 策略的基礎上進行改進,提出基于多滑模變結構控制的VIC 策略,得到以下結論:

1)內環采用基于指數趨近律的滑模電流控制,實現了對并網電流給定值的快速跟蹤,提高系統響應速度的同時抑制了并網電流諧波畸變;

2)外環建立虛擬慣性方程與滑模電壓控制,增強直流微網的慣性,有效抑制了直流母線電壓波動。

本文通過引入多滑模控制算法提升了BGC 系統的動、靜態性能,但虛擬慣性環節的參數Cv仍對母線電壓有較大影響。 文中虛擬電容Cv為固定值,無法兼顧系統的慣性和響應速度,下一步可針對參數Cv設計自適應調節算法,并研究其穩定邊界。