四階張量的Z-特征值包含集及其應(yīng)用

羅錦程, 趙建興

(貴州民族大學(xué) 數(shù)據(jù)科學(xué)與信息工程學(xué)院, 貴州 貴陽 550025)

1 預(yù)備知識

設(shè)m和n是正整數(shù),且m,n≥2.用[n]表示集合{1,2,…,n},用R(C)表示實(shí)(復(fù))數(shù)域,用Rn(Cn)表示n維實(shí)(復(fù))向量的全體,用R[m,n]表示m階n維實(shí)張量的全體.設(shè)

x=(x1,x2,…,xn)T∈Rn.

設(shè)

A=(ai1i2…im)∈R[m,n],

即

ai1i2…im∈R,ij∈[n],j∈[m].

Ax

滿足

▽Axm=mAx,

則稱A為弱對稱張量[1].

Axm-1=λx,xTx=1,

(1)

(Axm-1)

ρ(A)=max{|λ|:λ∈σ(A)}

弱對稱非負(fù)張量的Z-特征值和Z-特征向量在統(tǒng)計(jì)數(shù)據(jù)分析中的最佳秩一逼近中發(fā)揮著關(guān)鍵作用[4].張量的最佳秩一逼近,是求一個秩一張量κxm=(κxi1xi2…xim),使‖A-κxm‖F(xiàn)達(dá)到最小值,其中κ∈R,x∈Rn且xTx=1,‖A‖F(xiàn)為A的F-范數(shù)

Qi[5]證明了:κxm是A的最佳秩一逼近當(dāng)且僅當(dāng)κ是A的按模最大Z-特征值,x是與κ相對應(yīng)的Z-特征向量.Zhang等[1]證明了:若A是弱對稱非負(fù)張量,則ρ(A)是A的按模最大Z-特征值.因此,當(dāng)A是弱對稱非負(fù)張量時,ρ(A)xm0是A的最佳秩一逼近,x0是與ρ(A)相對應(yīng)的Z-特征向量,即

(2)

另外,在文獻(xiàn)[6-7]中,

(3)

被用來估計(jì)貪婪秩一更新算法的收斂速度.顯然，若ρ(A)的上界小于‖A‖F(xiàn),則可以給出(2)式和(3)式的非零下界.

最近,許多專家學(xué)者對張量A的Z-特征值和Z-特征向量進(jìn)行了定位(分布、估計(jì)和計(jì)算)[8-24],其中文獻(xiàn)[8]給出了A的Ger?gorin型Z-特征值包含集和Z-譜半徑的一個上界.

定理 1.1[8]設(shè)A=(ai1i2…im)∈R[m,n],則

其中

Ki(A)={z∈R:|z|≤Ri(A)},

R

定理 1.2[8-9]設(shè)A∈R[m,n]是非負(fù)張量,則

ρ(A)≤

為了對Z-特征值進(jìn)行更精確的定位,文獻(xiàn)[10]獲得了如下Brauer型Z-特征值包含集.

定理 1.3[10]設(shè)A=(ai1i2…im)∈R[m,n],則

其中

Ψi,j(A)={z∈R:(|z|-R

RΔji(A)Rj(A)},

RΔj

R

由定理1.3中的Z-特征值包含集,文獻(xiàn)[10]獲得Z-譜半徑的如下上界.

定理 1.4[10]設(shè)A∈R[m,n]是弱對稱非負(fù)張量,則

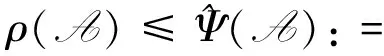
2 主要結(jié)果

RΔji(A)=

|a

|aijii|+|aiiji|+|a

|aijlk|+|aikjl|+|aiklj|+|ailkj|+|ailjk|),

R

|ailsk|+|aiskl|+|aislk|).

顯然

R

接下來,針對四階張量,給出一個比定理1.1和定理1.3中的Z-特征值包含集更精確的包含集.首先列出一個引理.

引理 2.1[11]設(shè)x=(x1,x2,…,xn)T∈Rn且

則

定理 2.1設(shè)A=(aijkl)∈R[4,n],則

其中

Ωi,j(A)={z∈R:

(|z|-r

rΔj

r

rij(A)=|a

證明設(shè)λ是A的Z-特征值,

x=(x1,x2,…,xn)T∈Rn{0}

0≤|xk|≤1,k∈[n].

0<|xt|3≤|xt|≤1.

λx

a

(atjtt+attjt+atttj)x

a

由引理2.1可得

|xj|3≤|xj||xj||x
|xj||xt|2≤|xj|,j≠t;
|xj|2|xk|≤|xj||xk||x
|xj||xk|2≤|xj||xk||x
|xk|3≤|xk||xt||x
|xj||xk||x
|xk|2|xl|≤|xk||xt||x
k≠l≠j;
|xk||xl||x
k≠l≠s≠j.

由此可得

|λ||xt|≤|atjjj||xj|3+


|atjtt+attjt+atttj||xj||xt||xt|+

atljk||xj||xk||xl|+|atttt||xt|3+

atklk+atlkk||xk||xk||xl|+

atslk||xk||xl||xs|≤


|atjtt+attjt+atttj||x
atjlk+atkjl+atklj+atlkj+atljk||xj|+
|atttt||x


atskl+atslk||xt|=
rΔjt(A)|xj|+r

即

(|λ|-r

(4)

λxj=a

a

ajlsk+ajskl+ajslk)xkxlxs

(5)

和不等式

|xt|3≤|xt|,

|xk||xt||x

得

|λ||xj|≤|ajttt||x

ajslk||xk||xl||xs|≤

|ajttt||x

ajskl+ajslk||xt|=rtj(A)|xt|,

即

|λ||xj|≤rtj(A)|xt|.

(6)

(|λ|-r

(7)

即

λ∈Ωt,j(A).

(8)

在(4)式中若|xj|=0,由|xt|>0可得

這時(7)式仍然成立.再由j的任意性得

進(jìn)一步，可得

定理 2.2設(shè)A=(aijkl)∈R[4,n],則

σ(A)?Υ(A)=

其中

Υi,j(A)={z∈R:|z|<

證明設(shè)λ是A的Z-特征值,

x=(x1,x2,…,xn)T∈Rn{0}

a

進(jìn)而得

|ajttt||xt|3≤|λ||xj|+

|λ||x

|λ||xt|+(Rj(A)-|ajttt|)|xt|3.

|λ|≥(2|ajttt|-Rj(A))|xt|2.

若2|ajttt|-Rj(A)>0,則由|x得

|λ|≥(2|ajttt|-Rj(A))|xt|2≥

(9)

若2|ajttt|-Rj(A)≤0,(9)式仍成立.

由(5)式得

a

再取絕對值并應(yīng)用不等式

max{|xk|3,|xk|2|xl|}≤

|xk||xt||x

|xt||xk||x

得

|ajttt||xt|3≤|λ||x

ajslk||xk||xl||xs|≤

|λ||x

ajskl+ajslk||xt|=

|λ||xt|+(rtj(A)-|ajttt|)|xt|,

進(jìn)而可得

|λ|≥|ajttt||xt|2-(rtj(A)-|ajttt|)≥

(10)

由(9)式和(10)式得

|λ|≥max

即λ?Υt,j(A).再由(8)式得

λ∈(Ωt,j(A)Υt,j(A)).

由j的任意性得

下面對定理1.1、定理1.3、定理2.1和定理2.2中的Z-特征值包含集進(jìn)行比較.

定理 2.3設(shè)A∈R[4,n],則

Υ(A)?Ω(A)?Ψ(A)?K(A).

證明由

Ωi,j(A)Υi,j(A)?Ωi,j(A),

i,j∈[n],j≠i

(|z|-r

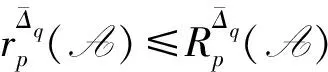
(|z|-R

(|z|-r

RΔqp(A)Rq(A),

因而可得

z∈Ψp,q(A)?Ψ(A).

設(shè)A是弱對稱非負(fù)張量,由定理2.1中的Z-特征值包含集Ω(A),并應(yīng)用類似于文獻(xiàn)[10]中定理5的證明可得ρ(A)的一個新上界.

定理 2.4設(shè)A∈R[4,n]是弱對稱非負(fù)張量,則

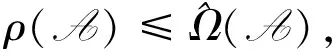
其中

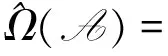
由定理2.3易得如下比較定理.

定理 2.5設(shè)A∈R[4,n]是弱對稱非負(fù)張量,則

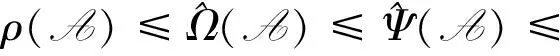
3 數(shù)值算例

例 3.1設(shè)A=(aijkl)∈R[4,2],其中

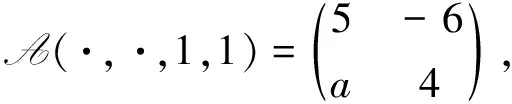
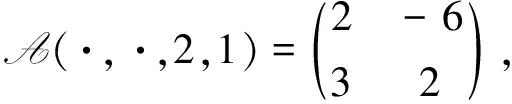
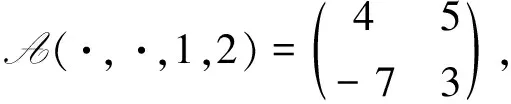
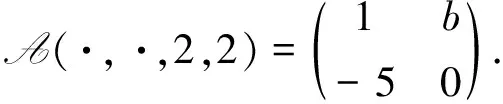
1) 當(dāng)a=0且b=1時,計(jì)算得A的所有不同Z-特征值為0和5.下面對A的所有Z-特征值進(jìn)行定位.由定理1.1得

K(A)={z∈R:|z|≤30}.

由定理1.3得

Ψ(A)={z∈R:|z|≤27.122 1}.

由定理2.1和定理2.2均得

Υ(A)=Ω(A)={z∈R:|z|≤5}.

容易看出

σ(A)?Υ(A)?Ω(A)?Ψ(A)?K(A),

K(A)={z∈R:|z|≤36}.

由定理1.3得

Ψ(A)={z∈R:|z|≤31}.

由定理2.1得

Ω(A)={z∈R:|z|≤6.140 1}.

由定理2.2得

Υ(A)={z∈R:1≤|z|≤6.140 1}=

[-6.140 1,-1]∪[1,6.140 1].

容易看出

σ(A)?Υ(A)?Ω(A)?Ψ(A)?K(A),

例 3.2設(shè)A=(aijkl)∈R[4,2],其中

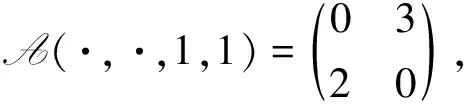
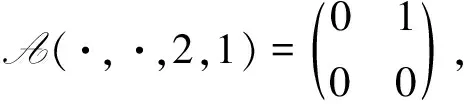
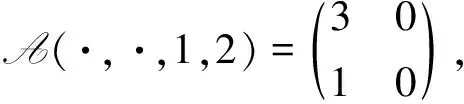
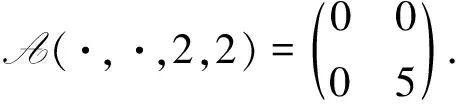
容易驗(yàn)證A是弱對稱非負(fù)張量.經(jīng)計(jì)算,得

(ρ(A),x)=(5.000 0,(0,1.000 0)T)

和

‖A‖F(xiàn)=7.000 0.

下面對A的Z-譜半徑ρ(A)進(jìn)行估計(jì).由文獻(xiàn)[8-10,12-22]中相應(yīng)定理得到的數(shù)值結(jié)果見表1.

表1顯示,由定理2.4得到的ρ(A)的上界小于由文獻(xiàn)[8-10,12-22]中相應(yīng)定理得到的上界,且僅有由定理2.4得到的上界小于

‖A‖F(xiàn)=7.000 0.

進(jìn)一步地,由(2)和(3)式可得

=

和

這個結(jié)果表明貪婪秩一更新算法的收斂速度至少為0.540 1.

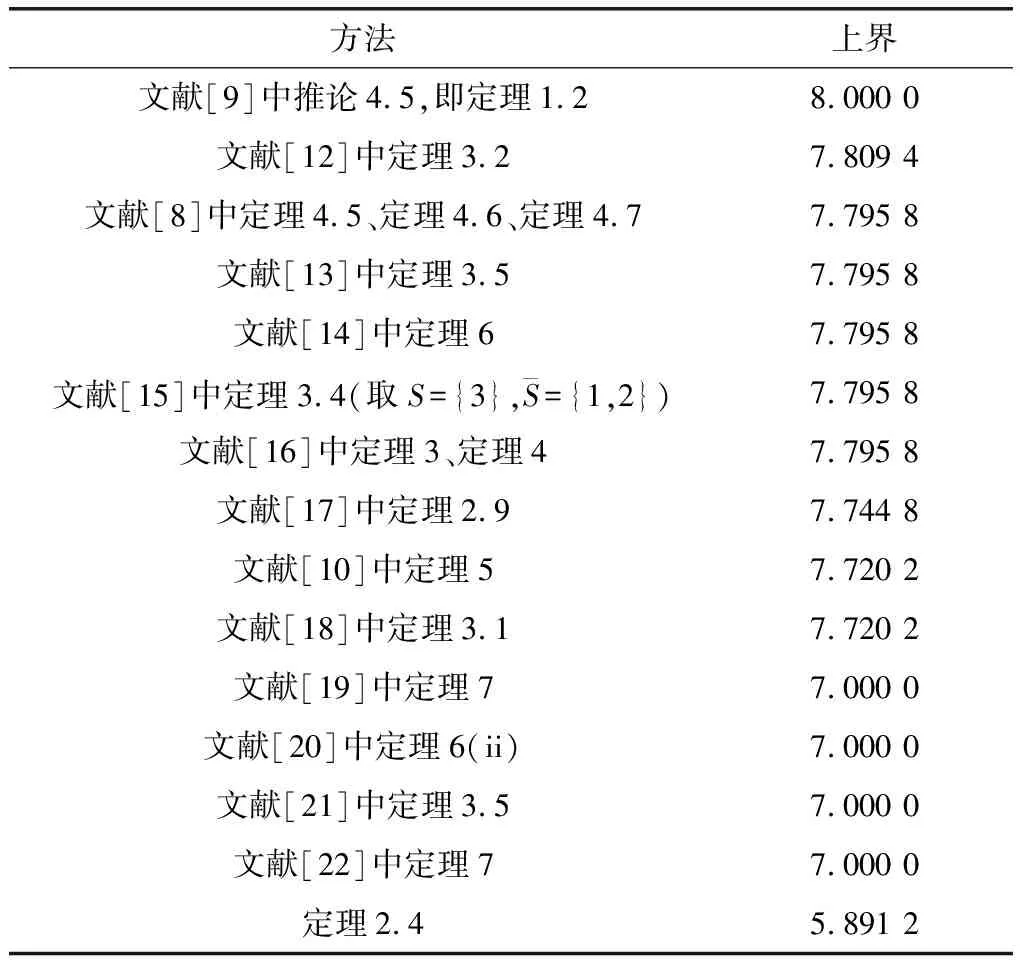
表 1 ρ(A)的上界