基于磁場-溫度場耦合的高壓開關柜梅花觸頭有限元數值計算

冀立鵬，甄 利，劉宏亮，董 馳，劉保凱，賈冬明

(1.國網河北省電力有限公司邢臺供電分公司，河北 邢臺 054001; 2.國網河北省電力公司，河北 石家莊 050021;3.國網河北省電力有限公司電力科學研究院，河北 石家莊 050000)

0 引 言

梅花觸頭憑借其接觸點多、導電性好和接觸電阻小等優點，被廣泛應用于電力系統當中[1-2]。梅花觸頭的作用主要是用于連接高壓設備，是一種彈性連接組件。目前，梅花觸頭發熱現象頻有發生，這將會引發一系列的電力系統故障，甚至會造成無法挽回的安全事故[3]。梅花觸頭在長期工作過程當中，由于觸頭的接觸不良或短路情況而引起過熱的現象，若未能及時處理就會導致熱故障的發生[4-5]。因此，梅花觸頭在實際工作過程中的接觸狀況和溫度場分布情況需要倍加關注。

目前，關于梅花接頭的研究文獻還較少，主要集中于實驗測量和仿真模擬兩個方面。在實驗測量方面，文獻[6]對高壓開關柜隔離觸頭的觸頭彈力進行了測量，并分析了系統誤差、環境影響和零件磨損對測量結果的影響。文獻[7]研究了接觸式和非接觸式的測溫傳感器在高壓開關柜觸頭實際安裝方式下的測量精度。由于實驗測量成本高，代價大，尤其是對故障情況下的實驗研究，具有一定的破壞性，因此計算機仿真模擬起到了很好的替代作用[8-9]。文獻[10-11]對帶有記憶合金材料的梅花觸頭進行了溫度場仿真和溫升試驗，分析了兩種異常接觸方式下梅花觸頭的安全性。文獻[12]建立了大電流開關柜仿真模型，通過分析和計算觸頭接觸電阻，進行不同載荷條件下開關柜多物理場耦合仿真。文獻[13]基于傳熱學基礎理論，利用COMSOL有限元分析軟件建立高壓開關柜觸頭的仿真模型，分析了觸頭溫度分布，總結出溫度檢測的最佳位置。文獻[14]基于電路和電磁場耦合關系模型，研究了插入式梅花觸頭的暫態溫升變化情況，計算了短路電流沖擊下觸點處最大溫度值。文獻[15]通過虛擬材料法和有限單元法模擬了梅花觸頭的溫度場分布情況，可以很好地體現出接觸電阻特性和多物理場耦合特性。為了研究梅花觸頭的電動設計可靠性和接觸失效原理，文獻[16]建立了梅花觸頭電動力計算模型，分析了短路情況下不同觸指結構的電動力分布以及接觸失效機理。上述文獻表明，采用實驗的方式模擬梅花觸頭的故障，成本高、代價大。而采用仿真方式進行故障模擬具有高效便捷的優勢。目前文獻中關于梅花觸頭的多物理場耦合仿真的研究僅針對某種單一工況進行了模擬，而多種故障工況下的梅花觸頭仿真有待進一步研究。

本文搭建了梅花觸頭三維仿真模型，通過分析導電橋模型和磁場-溫度場耦合數學模型的基礎理論公式，并基于有限元數值計算方法完成梅花觸頭在不同工作電流下的穩態多場耦合仿真和不同故障電流下的暫態多場耦合仿真。仿真結果可以很好為梅花觸頭在額定工況和故障工況下的運行狀態提供有效參考。

1 梅花觸頭模型與仿真

1.1 梅花觸頭三維結構模型

本文對GC5-1250/12 kV式梅花觸頭進行建模及仿真研究，利用Solidworks建模軟件所搭建的梅花觸頭仿真模型如圖1所示，從圖中可以看出該梅花觸頭模型主要由導體和觸頭構成。其中觸頭共有30個觸指，觸頭內部由銅合金材料構成，而導體內部材料由鋁合金構成，關于銅合金和鋁合金的材料參數如表1所示。為了降低多物理場耦合仿真的計算量以及復雜性，做出了如下3個假設：

表1 梅花觸頭的重要材料參數

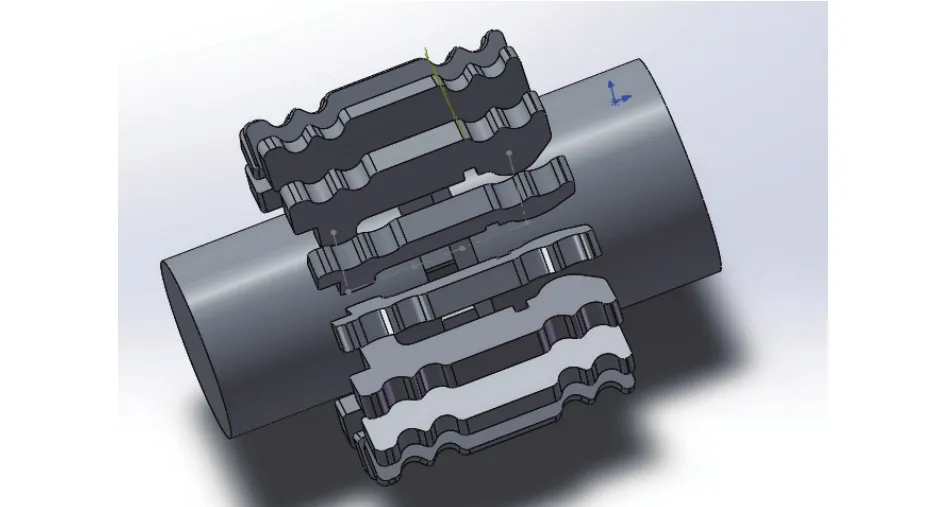
圖1 梅花觸頭三維結構模型

1）觸指與導體表面為彈性形變；

2）不考慮導電斑點間的分布及相互作用；

3）不考慮梅花觸頭材質的非線性特性。

1.2 導電橋模型

受制于梅花觸頭生產制作工藝的限制，觸指表面難以達到百分百的光滑程度，即難免存在微小的凹凸點，這些凹凸點會導致觸指表面與導體表面的實際接觸面積變小，電流在流動過程中聚集于微小凸點觸，該位置也相應地產生附加電阻值，即收縮電阻。本小節介紹了導電橋模型，該模型可以很好地模擬這一收縮效應。導電橋模型將電流在接觸面上傳導的過程視為通過一個等效導電斑點來實現，斑點的半徑可由如下Hertz公式得到：

式中：a——導電斑點半徑；

F——兩接觸平面的接觸壓力；

R*——接觸半徑；

E*——兩接觸物體材料的等效彈性模量。

對于由m根抱緊彈簧固定的梅花觸頭，單個觸點上接觸壓力為：

式中：Fj——單片觸指與導桿間的接觸壓力；

K——彈簧的剛度系數；

n——梅花觸頭的觸指數量；

D1、D0——導桿插入前和插入后彈簧的內外直徑平均值。

1.3 磁場-溫度場耦合數學模型

根據熱力學基本理論可以得到梅花觸頭的導熱方程如下所示：

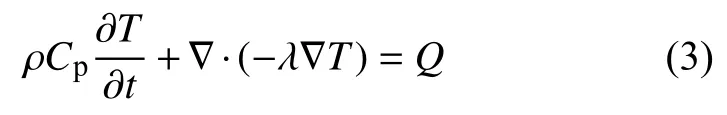
式中：ρ——導體密度；

Cp——導體的比熱容；

T——溫度；

t——時間；

λ——導體的導熱系數；

Q——內熱源。

忽略動靜觸頭內部的空氣流動，即對該區域只考慮熱量的內部傳導，而觸頭外部認為是以熱對流和熱輻射的形式進行散熱，因此需求出對流換熱系數和輻射換熱系數，根據傳熱學第三類邊界條件進行表征。對流換熱系數a為：

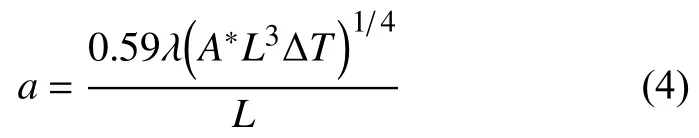
式中：λ——導體的導熱系數；

L——表面特征尺度；

ΔT——觸指與空氣的溫度差值；

A*——參數，值取決于流體的溫度和種類。

2 梅花觸頭磁場-溫度場耦合仿真結果分析

2.1 仿真計算流程

關于梅花觸頭溫度場仿真的整體流程如圖2所示。首先是依據梅花觸頭的結構參數構建出梅花觸頭仿真模型；然后利用ANSYS軟件對上述梅花觸頭三維進行單元剖分，其中剖分單元為四面體單元，節點數為37 953個，單元數為5 995個，網格剖分示意圖如圖3所示；再根據1.2小節中的導電橋模型，結合剖分后的仿真模型進行磁熱耦合有限元仿真計算。最后對梅花觸頭不同工況進行仿真，得到梅花觸頭在正常額定電流和故障短路電流下的溫度分布。

圖2 仿真計算流程圖

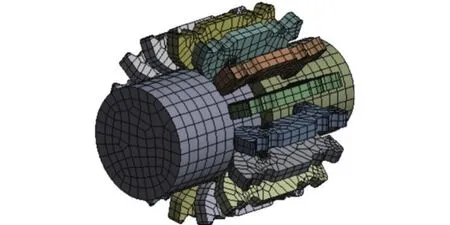
圖3 梅花觸頭網格剖分示意圖

2.2 計算結果與分析

首先是進行穩態磁場-溫度場耦合仿真，設定額定電流為1 250 A，梅花觸頭的初始溫度與環境溫度均為25 ℃，其對應的穩態溫度分布如圖4所示。從圖中可以看出觸指端部溫度最高，觸片本體溫度最低，其中最高溫度為51.929 ℃，最低溫度為51.338 ℃。而實驗所檢測出來的觸指端部溫度為52.1 ℃，與仿真結果基本保持一致，驗證了有限元仿真模型的準確性。

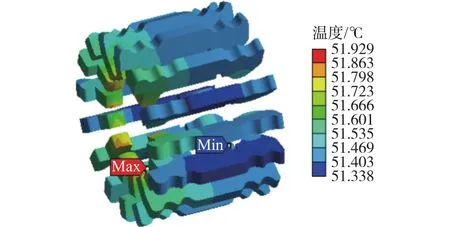
圖4 梅花觸頭在額定電流1 250 A時的溫度分布

不同穩態電流下梅花觸頭本體與觸指端部的溫度變化曲線如圖5所示。從圖中可以看出，隨著穩態電流的增大，本體溫度與觸指端部溫度均呈曲線增大趨勢，且觸指端部溫度要略大于本體溫度。該現象表明，觸指端部的接觸面上電流密度較大，熱生成率較高，因此導致溫度集中增大的現象。

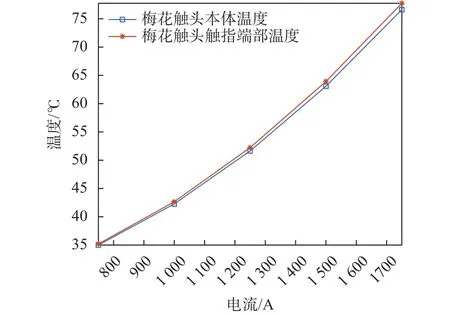
圖5 不同穩態電流下梅花觸頭的溫度變化曲線

高壓開關柜在發生短路故障時梅花觸頭承載的電流要遠高于額定電流，觸頭內部會在短時間內急劇升溫，從而會造成觸頭松動、接觸電阻增大情況發生，最終引發高壓開關柜安全事故。因此本文首先對梅花觸頭在30 kA時的暫態溫度分布進行仿真分析，研究短路工況下梅花觸頭的溫度分布情況。圖6為梅花觸頭在30 kA/5 s時的暫態溫度分布，其中最大溫度為101.98 ℃，最小溫度為34.301 ℃，兩者相差 67.679 ℃；圖7 為梅花觸頭在 30 kA/10 s時的暫態溫度分布，其中最大溫度為158.24 ℃，最小溫度為75.475 ℃，兩者相差82.765 ℃；圖8為梅花觸頭在30 kA/15 s時的暫態溫度分布，其中最大溫度為 236.86 ℃，最小溫度為 132.07 ℃，兩者相差104.79 ℃。仿真結果表明，短路工況下梅花觸頭的整體溫度均大幅上升，并且觸指溫度要明顯高于其他區域。

圖6 梅花觸頭在30 kA/5 s時的暫態溫度分布

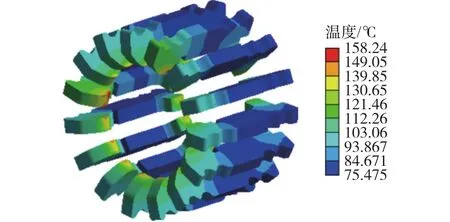
圖7 梅花觸頭在30 kA/10 s時的暫態溫度分布

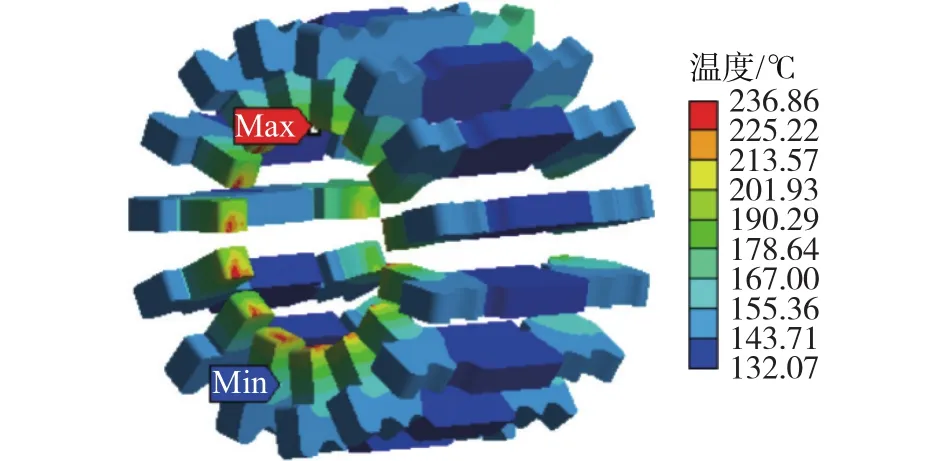
圖8 梅花觸頭在30 kA/15 s時的暫態溫度分布

當暫態電流為30 kA時，不同暫態時間下梅花觸頭的溫度變化曲線如圖9所示。從圖中可以看出，隨著暫態時間的增大，梅花觸頭的本體溫度和觸指端部溫度也逐漸增大。

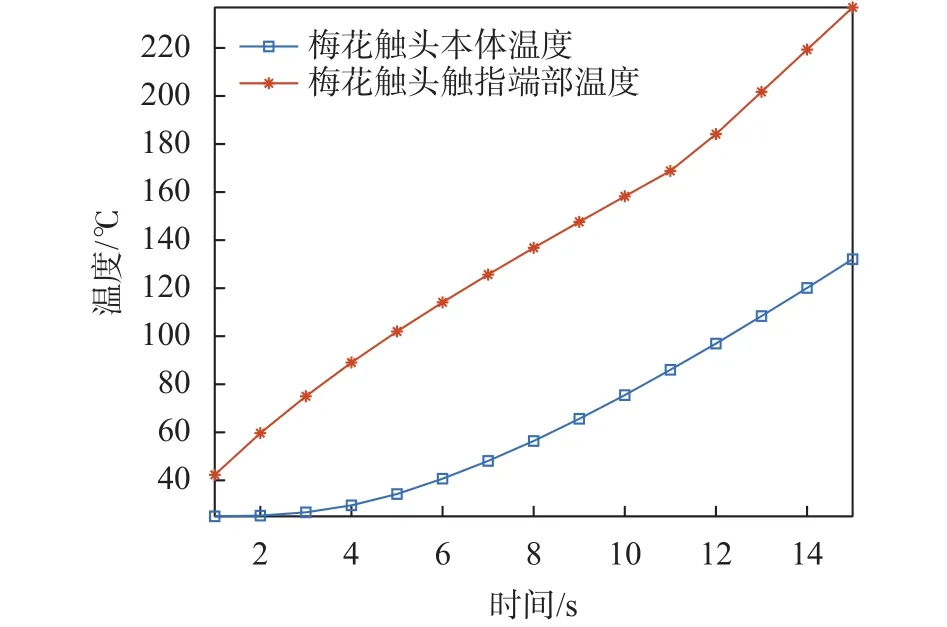
圖9 不同暫態時間下梅花觸頭的溫度變化曲線

當暫態仿真時長為15 s，此時不同暫態電流下梅花觸頭溫度變化曲線如圖10所示。當暫態電流在20～40 kA變化且逐漸增大時，梅花觸頭本體溫度和觸指端部溫度呈增大趨勢，兩者溫差較為明顯且隨著暫態電流的增大溫差也越來越大。

圖10 不同暫態電流下梅花觸頭的溫度變化曲線

3 結束語

本文基于磁場-溫度場耦合的有限元仿真研究了梅花觸頭在額定電流及短路故障下的溫度分布。文中根據梅花觸頭的結構參數和材料參數建立了三維有限元仿真模型，利用導電橋模型實現了梅花觸頭的多物理場耦合仿真，發現在1 250 A額定電流下梅花觸頭最高溫度出現在觸指處，且明顯高于其他區域。在穩態工作情況下，隨著額定電流的增大，梅花觸頭本體和觸指端部的溫度逐漸增大，兩者溫差較小。而在短路故障情況下，隨著短路電流的增大或暫態時長的增大，梅花觸頭的本體和觸指端部的溫度也不斷增大且遠高于額定狀態下的溫度，兩者溫度較大。在外加30 kA/15 s短路電流時，梅花觸頭的最高溫度可達到236.86 ℃。因此，在實際運行時要注意梅花觸頭的溫度監測以及觸指的結構設計。