基于缺失信號的圖重構
韓詩期 王俊義,2 李 然
1(桂林電子科技大學信息與通信學院 廣西 桂林 541004)2(“認知無線電與信號處理”教育部重點實驗室 廣西 桂林 541004)3(西安電子科技大學通信工程學院 陜西 西安 710071)
0 引 言
如何處理不規則域中的數據已經成為信號處理領域中的研究熱門。這些數據通常具有維度高、空間結構復雜的特點。由于極少考慮數據自身的空間結構和數據之間的交互,經典數字信號處理(Digital Signal Processing,DSP)方法在處理這類數據已經暴露出自身的局限性。處理不規則結構化數據的需求催生了圖信號處理[1-2](Graph Signal Processing,GSP)。在GSP中,信號的空間結構用由頂點和邊組成的圖來表示。圖的頂點表示實際結構中的實體,邊權重表示頂點之間的關系。定義在頂點上的標量值就是圖信號,對應于實際網絡中的觀測值。當前GSP領域的主要研究課題包括圖學習(Graph Learning)[3]、圖信號采樣[4]、圖信號重構[5]、圖信號降噪及濾波[6]等。GSP在許多具體任務中也取得顯著進展,如特征提取[7]、圖像處理[8]、視頻編碼[9]、聚類[10]和大數據分析[11]等。
許多基于圖的方法都假設圖是已知的或者可根據實際應用場景進行定義的,但是這些圖未必能真實反映數據的空間結構。而且對于許多數據而言,圖并非都是已知的。此外,傳統的圖學習方法通常都是在信號完備的情況下進行,而在實際應用中信號丟失的現象時有發生。因此,有必要對缺失信號的圖學習進行探究。使用缺失信號進行圖學習需要考慮兩個方面:1) 使用缺失信號學習圖,2) 利用學到的圖進行信號重構。每次迭代重構的信號都作為下一次學習圖的輸入。由于信號缺失,有必要對信號進行進一步約束,降低重構誤差,再反哺到圖學習中。傳統涉及到信號重構的圖學習中僅考慮了圖信號的空間光滑性。而在實際場景中,存在同時滿足空間光滑性和時間光滑性的信號。一個直觀的例子是溫度傳感器網絡,相鄰傳感器所采集到的溫度較為相似,同一傳感器在相鄰時刻采集到的溫度通較為相似。因此本文的創新性在于利用了圖信號在時間上的光滑性對圖學習中涉及到的信號重構問題進行修正。本文同時在合成數據和美國國家海洋和大氣管理局(National Oceanic and Atmospheric Administration,NOAA)官網溫度數據集上進行實驗,結果表明在信號缺失的情況下,本文的圖學習模型依然能合理推測信號的空間結構并進行信號重構。
1 相關工作
高斯圖模型是十分經典的圖學習模型。高斯圖模型學習的是變量的精度矩陣,即協方差矩陣的逆矩陣,因此也可以將其稱為協方差選擇問題。Dempster[12]為了能得到正態總體的稀疏結構,將精度矩陣中最小的值直接置零。而后,利用1罰函數實現稀疏學習的圖Lasso[13]成為了概率圖問題中廣泛使用的稀疏化學習模型。
GSP的發展為圖學習提供了新的思路。基于GSP的圖學習方法通常先建立圖信號的表示模型,再結合圖的稀疏性對模型進行優化。文獻[14]就信號處理的角度對圖學習進行詳細的闡述,將GSP的圖學習問題分為三類,分別是基于光滑信號[15-16]、譜濾波器[17-18]和圖上因果關系[19-20]的圖學習問題。基于信號光滑性的圖學習問題的前提條件是信號在相連的頂點上緩慢地變化。文獻[15]假設頂點度之和等于頂點數,借助因子分析法,從圖信號表示的角度構建了高斯圖模型。文獻[16]提出了一種新的模型,通過對數函數除去了Dong對于頂點度的約束,并使用原始對偶算法對模型進行求解,提升了計算效率。文獻[17-18]學習的是平穩圖信號的底層結構,濾波器是圖移位算子的高次冪,并用圖移位算子表示圖。圖信號的經驗方差就是圖濾波器的特征向量,再對濾波器特征值矩陣降冪、恢復特征值符號,最終得到圖移位算子。文獻[19]借助稀疏向量自回歸(Sparse Vector Autoregressive,SVAR)模型表示圖上的因果過程。文獻[20]使用結構化方程模型(Structural Equation Model,SEM)表示信號變化過程。
信號重構也廣泛使用了基于圖的方法,包括帯限信號重構[5,21]、低秩信號重構[22]和時變信號重構[23-24]等。許多圖信號重構的方法都充分利用了信號在空間圖上的光滑性。為降低信號重構誤差,部分研究者開始考慮同時利用信號空間和時間兩個維度的信息。文獻[25]在進行矩陣填充時根據矩陣的行和列構造了行圖和列圖,同時利用了信號矩陣行和列的光滑性。文獻[26-27]則提出了聯合圖傅里葉變換,其中根據信號矩陣的列向量構成的圖就是頂點圖或空間圖,根據行向量構造的圖就是時間圖,并證明了聯合圖就是空間圖和時間圖的笛卡爾積。實際上存在涉及到信號重構的圖學習問題[15,20],其中的保真項可以看作是采樣率為1時的聯合圖學習和信號重構問題。
2 圖學習模型
2.1 基本概念
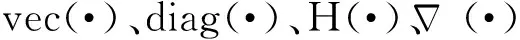


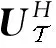
文獻[27]提出聯合圖傅里葉變換(Joint Time-Vertex Transform,JFT)就是分別對信號矩陣的列向量做GFT,對行向量做DFT,聯合圖就是時間圖和空間圖的笛卡爾積,即直積。假設存在信號矩陣X=[x0,x1,…,xT-1]∈RN×T,空時圖的組合拉普拉斯矩陣L和JFT分別定義為:
L=L?L=L?IN+IT?L=

(1)
(2)
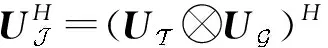
vec(X)TLvec(X)=tr(XTLX)+tr(XLXT)
(3)
顯然,圖信號的空間光滑性和時間光滑性是相互獨立的。衡量信號在聯合圖L上的光滑性就是分別衡量其在空間圖L和時間圖L上的光滑性。
2.2 缺失信號的圖學習模型
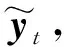
(4)

(5)

(6)

(7)

(8)
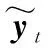


(9)
(10)
(11)
ht關于yt的條件分布滿足:
p(ht|yt)∝p(yt|ht)p(ht)
(12)
因此ht關于yt的最大后驗估計為:
(13)

(14)
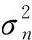
其矩陣形式為:
(15)
式中:Y=[y0,y2,…,yT-1]∈RN×T為觀測值,即缺失信號,N為頂點數,T為時間序列長度。X∈RN×T為待恢復的信號。J∈RN×T為采樣矩陣,Jij∈{0,1},i=1,2,…,N,j=0,1,…,T-1。式(3)表明空間變分與時間變分是可分離的,再考慮圖的稀疏性和信號的時間變分,式(15)可以進一步寫為:
(16)
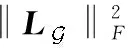
2.3 模型求解
為保證解的有效性,有必要向式(16)中的目標函數添加約束條件,最終需要求解的目標函數為:
(17)





(18)



圖信號重構問題為:
(19)
可以將全部求解過程概括為算法1。
算法1模型求解
輸入:Y,J,α,β,γ,迭代次數,容許誤差。
1.初始化:X0=Y,k=1
2.重復
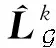
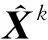
5.3)k=k+1
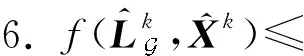


(20)



式(20)中目標函數的梯度和Hessian矩陣可得:


2.3.2信號重構
信號重構的目標函數為:
(21)
vec(Y-J°X)Tvec(Y-J°X)+

vec(Y-X)TQvec(Y-X)+


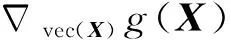
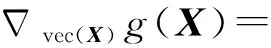


(22)

Hessian是半正定矩陣,矩陣因此信號重構問題是無約束凸優化問題。
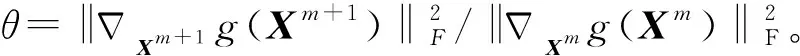
(23)
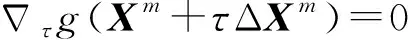
(24)
共軛梯度法見算法2。
算法2共軛梯度法

輸出:重構的圖信號Xm。
1.初始化:X0=0N×T,ΔX0=0N×T,m=0
2.重復
3.1) 根據式(24)選擇合適的更新步長τ
4.2) 共軛梯度方向更新步驟
5.Xm+1=Xm+τΔXm
8.m=m+1
9:‖ΔXm‖F≤δ或到達最大迭代次數時停止
3 實驗結果分析
3.1 合成數據

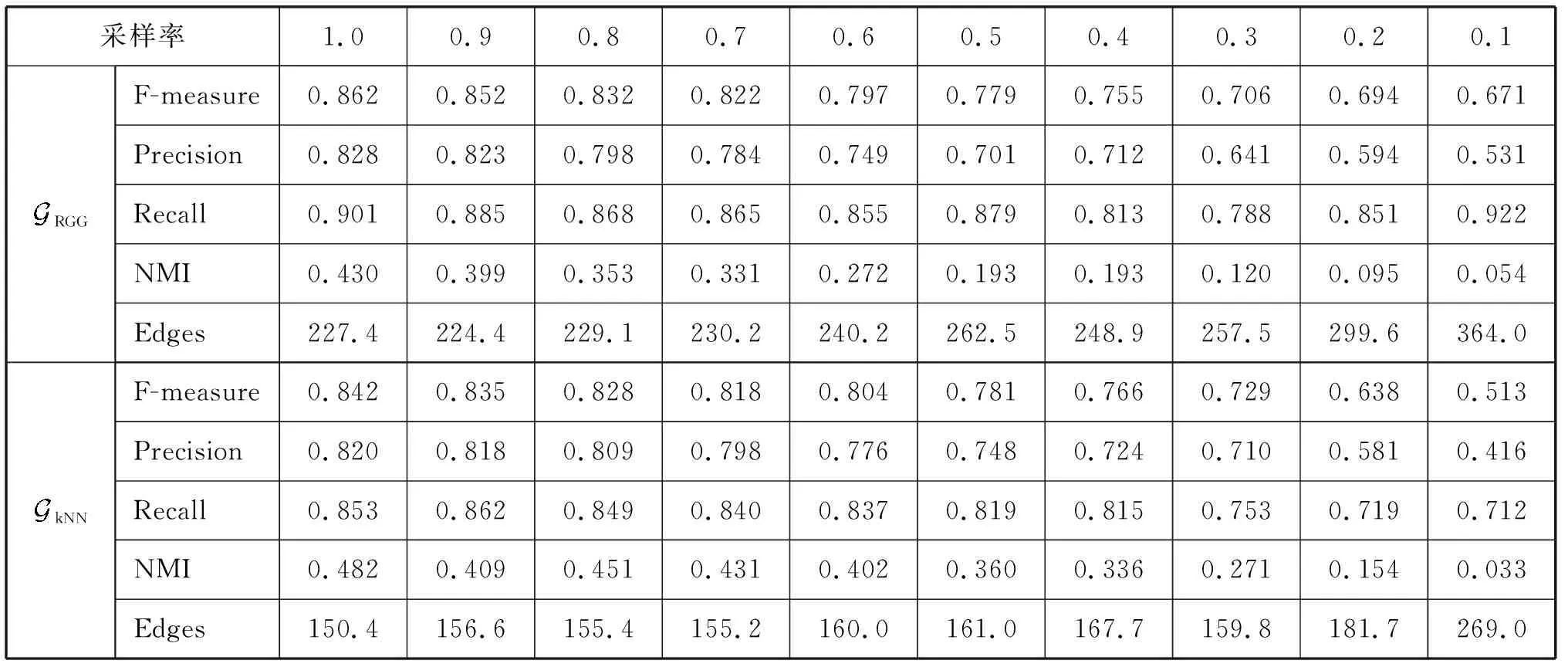
表1 不同采樣率圖信號的圖學習效果


表2 本文圖學習模型和已知圖的信號重構效果對比
3.2 實測溫度數據
對于實測數據,由于原圖未知而無法直接進行對比。拉普拉斯矩陣的一個重要應用就是譜聚類,所以可以根據譜聚類性能來間接判斷所學習拉普拉斯矩陣的好壞。評價聚類性能使用的指標包括蘭德系數(Rand Index,RI)、純度(Purity)和NMI,上述三項指標值越大,譜聚類性能越好。聚類效果越好,說明學到的圖越準確。由于是在信號缺失的情況下進行圖學習,因此評價模型性能還需要考慮圖信號重構誤差。當聚類性能越優越,圖信號重構MAE越低,模型性能越好。
本文所使用的溫度數據來自于NOAA官網,采集了中國大陸60個不同地區氣象站在2018年1月至8月共243天的日均溫,信號矩陣大小為60×243。由于溫度在時域上是均勻采樣,所以可以認為溫度在時域內是光滑信號,因此可以使用時間變分法的約束。同時,相鄰氣象站之間采集到的溫度更為接近,因此該數據集同樣滿足空間光滑性,也可以將其看作是在傳感器個數為60的溫度傳感器網絡以相等時間間隔采集了243次數據。在進行實驗前根據氣象站所在的氣候帶對其進行標簽分類。所涉及的氣候帶包括溫帶大陸性氣候、高原山地氣候、溫帶季風氣候和亞熱帶季風氣候,因此將樣本簇的個數定為4,不同氣候帶上的氣象站個數均為15。
一種重構無線溫度傳感器網絡信號的方法是根據傳感器坐標選擇合適的k值構造kNN圖,再利用kNN圖進行圖信號重構[24]。文章利用氣象站坐標分別構造了k=2,3,5,8時的kNN圖,并給出了不同kNN圖和本文圖學習模型對氣象站進行譜聚類與圖信號重構結果進行對比,見圖1。如圖1至圖3所示,對于kNN圖而言,k=2時的聚類效果最好,RI、Purity和NMI值均最高。在采樣率不低于0.5時,圖學習模型譜聚類各項指標基本達到k=2時kNN圖的效果。隨著采樣率的增加,圖學習的方法各項性能指標逐漸優于k=2時的kNN圖。其中圖學習模型的RI值和NMI值略優于kNN圖,而Purity值遠勝于kNN圖。從圖4可以看出,圖學習模型的信號重構MAE值最小,效果最佳。可以認為在信號缺失時,本文圖學習模型學到的圖比kNN圖更客觀地反映了不同位置氣象站之間的關系。
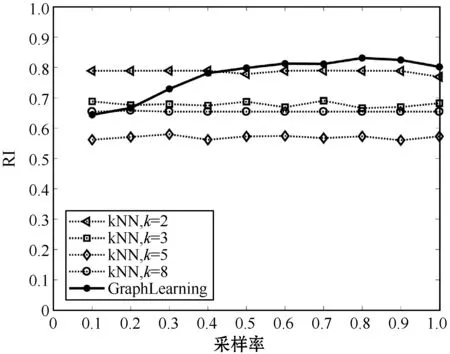
圖1 RI值
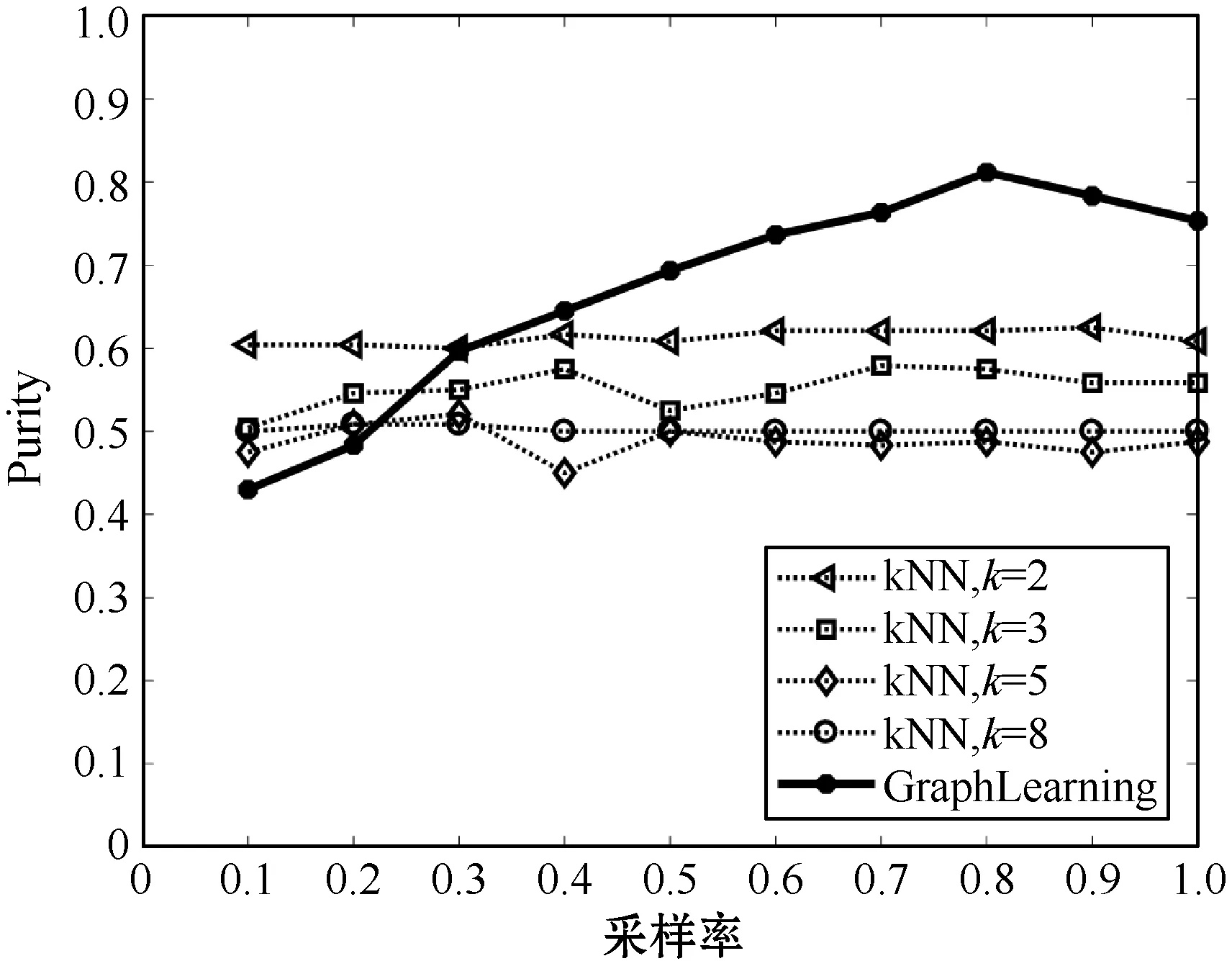
圖2 Purity值

圖3 NMI值
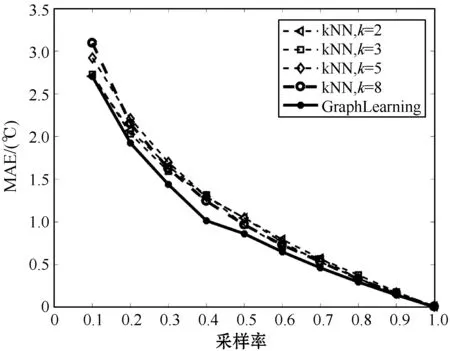
圖4 MAE值
4 結 語
本文構造了缺失信號的圖學習模型,同時利用信號的時間變分和空間變分對信號進行重構,并通過數值實驗證明了在信號殘缺的情況下,本文的圖學習模型依然能夠合理地學習數據的空間結構,圖信號重構效果也略優于直接構造圖的方法。下一步的研究可以分為兩部分:一是開發適用于大規模圖的圖學習算法;二是將缺失信號圖學習模型應用到實際場景中,如信號重構、數據異常檢測等。

