基于速度場的露天礦卡車多路段行程時間組合預測模型

田鳳亮， 王忠鑫，2， 孫效玉， 辛鳳陽， 宋波， 王金金， 曾祥玉， 周浩， 趙明

（1. 中煤科工集團沈陽設計研究院有限公司，遼寧 沈陽 110015；2. 遼寧工程技術大學 礦業學院，遼寧 阜新 123000；3. 東北大學 資源與土木工程學院，遼寧 沈陽 110015）

0 引言

就露天礦電鏟-卡車間斷工藝生產效率而言，1個卡車作業周期內卡車行程時間的占比最高、變動幅度最大。準確的卡車行程時間預測是卡車優化調度的前提。受制于露天礦復雜多變的道路條件，實際生產中卡車優化調度系統在相當長一段時間內只實現了調度而非優化[1-3]，其中一個重要原因是卡車在復合路段上的行程時間難以精準預測。

露天礦卡車行程時間受卡車性能、道路狀況與環境因素的共同影響。一般來說，卡車行程時間可通過人工統計獲取。但由于露天礦道路變動頻繁，人工獲取的時間往往很難用于生產組織工作[4]。當一條道路上的行程時間數據量足夠支撐行程時間統計結果時，該道路可能已接近廢棄。

在市政交通領域，國內外專家學者結合實際開展了行程時間預測研究[5]，預測方法主要有歷史趨勢法、參數回歸模型、時間序列、神經網絡、支持向量機、卡爾曼濾波等[6-10]。露天礦卡車行程時間預測也可采用上述方法。從研究對象角度出發，可將露天礦卡車行程時間預測問題分為固定路段預測與動態預測兩類[10]。固定路段行程時間預測的研究對象為固定起點與終點路段上的行程時間，而動態行程時間預測則研究道路上任意2點之間的行程時間。

固定路段行程時間預測的研究單元為單一路段。白潤才[1]針對人工統計平均速度方法的局限性，提出了基于人工神經網絡的露天礦卡車路段行程時間實時預測方法，較人工方法在預測精度和操作復雜度上都有明顯改善。E. K. Chanda等[9]針對人工神經網絡迭代次數多、收斂速度慢、容易陷入局部最小值而非全局最小值的問題，提出了基于自適應神經網絡模糊系統的露天礦卡車行程時間預測方法，較人工神經網絡在收斂速度和預測精度上有了進一步改善。Sun Xiaoyu等[10]提出了一種基于隨機森林的卡車行程時間預測方法，將道路長度、卡車型號、駕駛人員等作為輸入，獲得了較高的預測精度。

與固定路段行程時間預測相比，動態行程時間預測更具實用性。孟小前[4]通過研究認為，進行露天礦卡車動態行程時間預測時，支持向量機的預測結果在一定程度上優于BP神經網絡。K. Erarslan[11]研發了一套計算機輔助系統來預測卡車行程時間，可實時采集卡車速度，將距離除以速度來獲得卡車行程時間預測結果。

上述文獻研究的卡車行程時間預測方法或是在機理上進行細致刻畫，或是從統計角度進行描述，預測結果往往具有很高的準確性。但露天礦道路復雜，導致上述理論方法在實際部署中存在困難。鑒此，本文提出一種基于速度場的露天礦卡車多路段行程時間組合預測模型，以歷史數據構建卡車速度場，用于表征道路對卡車速度的影響，在此基礎上分路段建立基于隨機森林的行程時間單元預測模型，最終將單元預測模型預測結果累加，得出卡車在復合路段的行駛時間預測值。

1 多路段行程時間組合預測模型原理

露天礦卡車多路段行程時間組合預測模型由單元預測模型、累加器、速度場組成，其原理如圖1所示。單元預測模型負責預測卡車在每一路段所需的具體時間。但該時間受卡車在路段上行駛的平均速度影響，而平均速度同樣為未知數。這就要求在預測卡車行程時間之前，先估計卡車在該路段的平均速度。平均速度估計依賴卡車速度場，其可給出該路段任意一點上卡車可能的速度。以該速度為基礎，單元預測模型可預測卡車經過該路段所需的時間。累加器負責將每個單元預測模型的預測結果相加，并作為最終預測結果輸出。

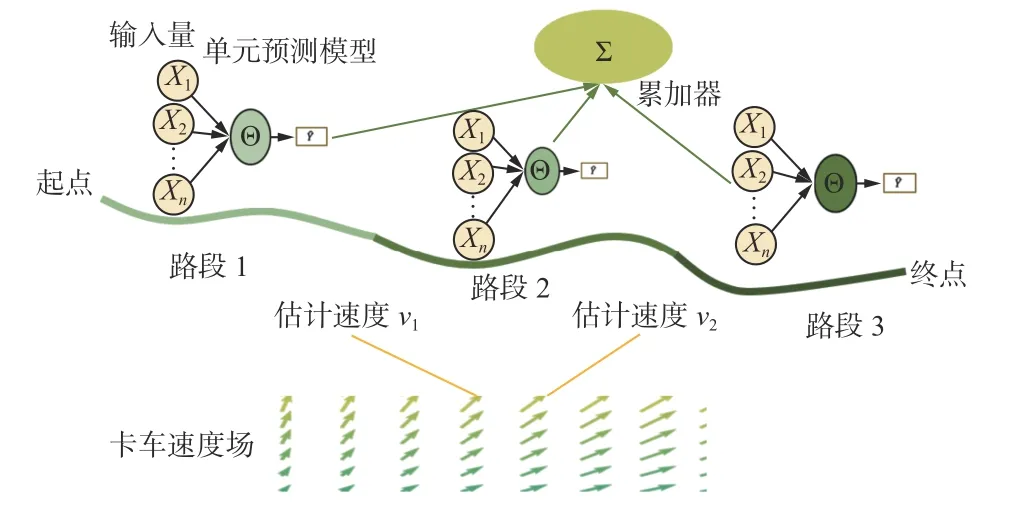
圖1 露天礦卡車多路段行程時間組合預測模型原理Fig. 1 Principle of combined prediction model of multi section travel time of truck in open-pit mine

1.1 卡車速度場構建

場指物體在空間的分布情況，一般以空間位置函數表示。本文引入場的概念來表征卡車在整個礦區各條道路上的速度分布情況。卡車速度場反映了卡車速度與其在道路上具體位置的關系，卡車在道路上的位置不同，其速度也不同，如圖2所示。其中x，y分別為礦區二維坐標，箭頭指向為卡車行進方向，箭頭長短表示卡車速度，箭頭越長則速度越快。可看出當卡車行駛在右側路段時，速度始終偏小；當卡車駛入左側路段后，速度明顯提升。這也驗證了在預測卡車行程時間時，將整個行程作為研究對象是不合理的。

圖2 露天礦卡車速度分布Fig. 2 Speed distribution of truck in open-pit mine

速度場可看作典型的二維場模型。二維場模型一般可通過不規則分布點法、規則分布點法、矩形區域法、不規則三角形法等表征[12]。速度數據在空間上均勻分布于各條道路，采用矩形區域法表征較合理。因此，選擇矩形區域法表征卡車速度場。將整個礦山所在區域離散化為二維網格，將采集到的卡車速度信息映射到對應網格中。每個網格中的屬性值為該網格中卡車速度平均值。當網格中無對應速度信息時，網格屬性值為0。

露天礦卡車速度場如圖3所示。顏色越亮，表示速度越大。可看出卡車在不同路段上的速度不同，在道路終點、兩側、交叉口處存在明顯的減速現象。

圖3 露天礦卡車速度場Fig. 3 Truck speed field in open-pit mine

1.2 單元預測模型選擇

從統計角度看，卡車行程時間具有明顯的規律性。但卡車行程時間是多因素耦合的結果[13-15]，影響因素大致分為卡車屬性、環境特征、道路因素3類。卡車屬性主要包括卡車型號和載重狀態。針對不同的生產需求，露天礦中卡車型號往往有多種。這些卡車的購入時間、保養狀況、動力條件等不盡相同。卡車作業時分為空載和重載2種狀態，重載狀態下卡車行駛速度較慢。環境特征主要包括氣象條件、晝夜變化等。露天礦卡車在不同季節的行程時間不同，晝夜行程時間也不同。道路因素主要指卡車行駛的路線信息，包括卡車行駛的起點、終點位置及其所經過路段的長度、提升高度等。道路因素是影響卡車行程時間最重要的因素。道路長度與提升高度會極大地影響卡車行程時間。當其他因素不變時，道路越長，提升高度越大，則卡車所需的行程時間越長。

卡車在路段上的平均速度影響卡車行程時間。定義卡車在某路段s上的速度為v（s），則理想狀況下卡車行駛時間為

卡車速度不同時，其在該路段的行駛時間不同。

可見，影響卡車行程時間的主要因素有卡車型號、卡車載重狀態、氣象條件、卡車所經路段及其在該路段上的平均速度。這些因素有的是連續量，如道路長度、提升高度等；有的是離散量，如卡車型號、氣象條件等。若采用支持向量機等算法，則需將離散信息量化，不可避免地存在一定程度的主觀性。為了降低量化的主觀性造成的精度損失，采用隨機森林算法構建行程時間單元預測模型[16-18]。隨機森林算法由多棵決策樹組成。在構建決策樹時，從訓練數據集中有放回地隨機選取部分樣本，且隨機選取部分特征進行訓練。每棵決策樹使用的樣本和特征不同，訓練結果也不同，可避免模型出現過擬合現象。

單元預測模型的輸入包括卡車在所經過路段上的平均速度及文獻[10]中的輸入量，包括卡車ID、卡車類型、卡車狀態、路段起點及終點位置、道路信息、氣壓、風速、溫度、相對濕度、行駛時間等。

1.3 卡車平均速度計算

卡車在所經過路段上的平均速度是卡車行程時間預測的重要參數。將道路劃分為多個單一路段后，單元預測模型并行計算每條路段上的卡車行駛時間。卡車在不同路段上的速度不同，而速度場只反映道路上各點卡車速度平均值，不是卡車在具體路段的平均速度，因此，對整條路段上所有點的卡車速度求平均值，將其近似為卡車在該路段的平均速度，即

式中：R為某路段上的所有網格區域；N為R中網格數；vr為網格r中卡車速度。

卡車不可能經過R中所有網格，因此只能近似表示卡車實際平均速度。本文中單元預測模型為隨機森林算法，其為一種典型的統計學習算法，盡管并不嚴格等于平均速度，但在統計意義上依然是一種有效輸入。以作為單元預測模型的輸入，能更準確地預測卡車經過該路段所需的時間。

2 實驗與結果分析

以2019年6-11月華能伊敏煤電有限責任公司伊敏露天礦卡車調度系統中220 t卡車1.8萬條行程信息為基礎數據，將其中1.5萬條數據作為訓練集，剩余0.3萬條數據作為測試集，研究露天礦卡車多路段行程時間組合預測模型精度。采用隨機森林擬合算法預測卡車行駛時間，以sklearn機器學習庫中的RandomForestClassifier構建預測模型。采用分散訓練、集中使用策略，先分別訓練各路段上的單元預測模型，之后利用速度場將各單元預測模型整合。

模型輸入變量中，離散量（如設備型號、日期、時間等）可直接輸入模型，連續量中需要注意的是，道路信息既包括道路水平長度，也包含豎直方向的提升高度。本文通過計算道路中心線的方式獲取道路信息。定義某路段上點的集合為P={x0，y0，z0，x1，y1，z1，···，xm，ym，zm}，（xi，yi，zi）為 該 路 段 上 第i（i=1，2，…，m）個點的坐標，m為該路段上的點數。則該路段水平長度為

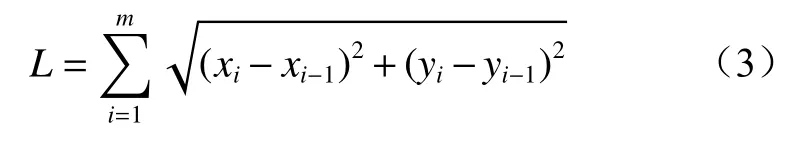
當卡車在該路段上處于上坡行駛時，提升高度為

式中zmax，zmin分別為運輸過程中高程最大值與最小值。

當卡車處于下坡行駛時，提升高度為

對于大多數機器學習算法，需采用梯度下降方法求解最優解。為了保證模型有解，同時提高迭代速度，對輸入的各連續變量進行歸一化處理。

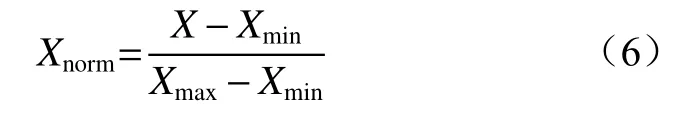
式中：Xnorm為輸入量歸一化值；X為輸入量；Xmin，Xmax分別為輸入量最小、最大值。

在模型訓練過程中，采用窮舉方法，通過在訓練集中交叉驗證方式尋找決策樹數量最優值（本文為75）。該過程中參數設置：弱學習器數量為5～150，搜索步長為5，交叉驗證可迭代次數為10。

采用測試集驗證模型精度，預測結果與真實值之間的誤差分布如圖4所示。可看出預測誤差主要集中在0～40 s，90%以上的預測誤差小于1 min，1～2 min誤差極少。通過分析誤差來源，發現誤差較大的行程時間其對應的路段數較多。

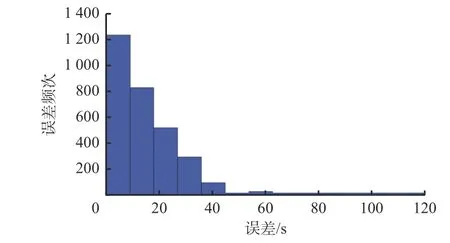
圖4 組合預測模型的預測誤差分布Fig. 4 Prediction error distribution of the combined prediction model

采用平均絕對誤差百分比（Mean Absolute Percentage Error，MAPE）檢驗模型預測精度[19]。經計算，本文模型對卡車行程時間預測的MAPE為4.81%。

為了驗證本文模型引入速度場及組合預測方法的優勢，將其與文獻[10]中的行程時間預測模型進行對比。基于相同的數據集，文獻[10]模型的預測誤差分布如圖5所示。經計算，MAPE為7.02%。

圖5 文獻[10]中模型的預測誤差分布Fig. 5 Prediction error distribution of the model in reference [10]

對比圖4、圖5可看出，本文模型所得結果較文獻[10]方法準確，在相同的數據集下，MAPE降低2%以上。特別是針對地表維修站-坑下工作面之間幾條較長的道路，本文模型的預測精度優勢更明顯：本文模型預測誤差基本不超過120 s，而文獻[10]中模型預測誤差為100～215 s。

為了明確預測精度提高的原因，選取若干單一路段作為實驗對象。經計算，在單一路段上，本文模型的MAPE為4.01%，文獻[10]中模型的MAPE為4.33%，二者差別不大。文獻[10]中預測模型也是基于隨機森林算法構建的，與本文模型在特征選取及參數設置上無太大區別。不同之處是，本文模型考慮了每一條路段的特殊情況，是一種路段組合模型，且模型充分考慮了卡車在道路上行駛的平均速度。可見，將單一模型進行組合可有效提高預測精度。

本文模型輸入量包括平均速度，因此在卡車處于任意位置、速度情況下，模型均能預測到達目的地的時間，即可實現卡車行駛時間動態預測。實時性是動態預測的重要指標。模型從接收數據到輸出預測結果的平均運算時間如圖6所示。可看出模型運算時間不超過1 s，可實時預測露天礦卡車行程時間。

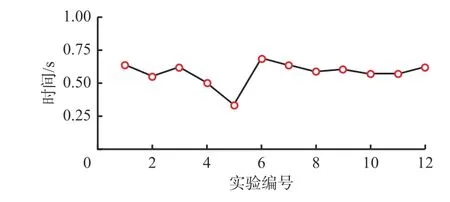
圖6 組合預測模型運算時間Fig. 6 Operation time of the combined prediction model

3 結論

（1） 基于速度場的露天礦卡車多路段行程時間組合預測模型具有較高的預測精度，其MAPE較文獻[10]中模型降低2%以上。

（2） 針對單一路段的行程時間預測，組合預測模型與單一模型相比無太大差別；針對復合路段行程時間預測，組合預測模型預測精度較單一模型高。露天礦實際生產中更多的是由不同行駛條件路段組成的復合道路，因此組合預測模型更適用于露天礦卡車行程時間預測。

（3） 露天礦卡車多路段行程時間組合預測模型中引入速度場，以卡車平均速度作為模型輸入量之一，使得卡車行程時間動態預測成為可能。實驗結果表明，該組合預測模型的運算時間不超過1 s，可實時預測卡車行程時間。