基于單純形法改進的混沌控制算法

夏雨 湯峰 余穎燁

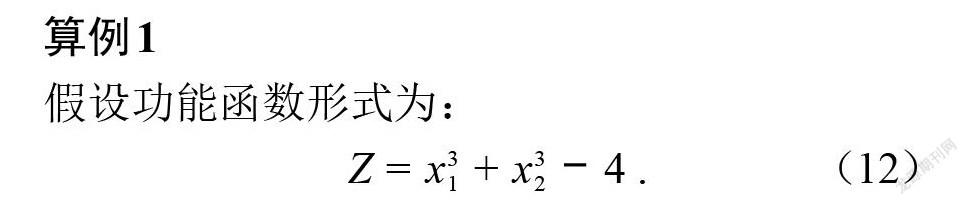
摘? ?要：混沌控制（chaos control，CC）算法在求解結構可靠度問題中具有優越的穩健性，但由于其對步長的嚴格限制，導致計算速度較慢。單純形法是一種不將梯度方向作為尋優方向的算法，該算法初始計算速度較快，能夠迅速逼近至極限狀態面附近，此后計算速度明顯下降，且計算結果誤差較大。為此，提出一種基于單純形法改進的混沌控制算法。首先，通過增廣乘子法將可靠度計算中的非線性等式約束問題轉化為非約束問題;然后，通過單純形法進行初始迭代計算;最后，使用CC算法進行收斂計算。算例結果表明：本文算法能夠有效解決高非線性功能函數可靠度求解問題，且兼具兩種算法的優點，與混沌控制算法相比，提高了計算效率。

關鍵詞：結構可靠度;混沌控制算法;單純形法;可靠度計算;計算效率

中圖分類號：TU311.4? ? ? ? ? ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2022.03.008

0? ? 引言

建筑結構的安全性與穩定性對人類社會影響巨大，如何對其進行合理評價至關重要。Freudenthal[1]在《結構安全度》一文中提出了結構可靠度的相關概念;為了得到結構可靠度指標，Cornell等[2-4]提出了一次可靠度理論，并對其不斷完善。然而當結構功能函數的非線性程度較大時，經典一次可靠度計算方法往往會出現迭代振蕩、結果不準確的情況。為了解決上述問題，眾多學者展開了更進一步的研究。Liu[5]首先考慮引入merit函數作為評價函數，但是該函數并不能保證算法的迭代方向為下降方向;Zhang等[6]考慮引入Armijo準則進行迭代步長的調控;楊迪雄[7]基于混沌控制理論中的穩定轉換法，通過引入步長調控因子提出了混沌控制（chaos control，CC）算法，但由于該方法對步長的嚴格限制，致使算法計算速度相對較慢;Meng等[8]針對CC算法中存在的問題，結合“之”字型迭代路徑，提出了修正混沌控制（modified chaos control，MCC）方法。目前學術界對于Armijo準則的研究也有了不少的成果[9]，而李彬等[10-11]則將Armijo準則引入到混沌控制算法中，使得計算速度進一步加快，并且進行了逆可靠度求解方法的嘗試。與此類似，亢戰等[12]提出的修正迭代算法中也提及了步長調控因子的控制作用，在文中將其定義為修正系數，并給出了修正系數的具體計算方法。

除此之外，貢金鑫[13]還對迭代點在極限狀態面上的負梯度方向進行了深入研究討論，提出了有限步長法，并推理出HL-RF算法只是有限步長法的一個特例，該方法的初始步長會影響算法的收斂性。吳狄等[14]提出了自動變步長的搜索方法，但是收斂速度較慢。王林軍等[15]使用外罰函數法進行可靠度計算，但是由于該方法將其中一個變量用剩余變量進行表示，算法魯棒性不好，不夠穩定，應用受限。高翔等[16]則將模擬退火法與增廣乘子法應用到可靠度計算中，雖然避免了一次二階矩方法中梯度的求解問題，但是卻增加了迭代步驟。許家赫等[17]將自適應性PSO算法與fmincon函數結合用于尋優計算，拓展了可靠度指標的計算方法。就目前而言，FOSM方法在結構可靠度分析方面的理論研究已經比較成熟，但是在實際的工程可靠度分析中卻鮮有使用，主要原因是：如果結構的功能函數非線性程度過高，那么將會導致求解過程復雜化，致使整個計算過程效率低下，誤差也比較大，所以如何實現快速、準確求解是當前有待解決的一個? ? ?問題。

針對上述問題，本文提出一種基于單純形法改進的CC算法。首先，通過增廣乘子法將可靠度計算中的非線性等式約束問題轉化為非約束問題;然后，通過單純形法進行初始迭代計算;最后，使用CC算法進行收斂計算，通過數值算例驗證了本文方法的計算準確性與效率。

1? ? 可靠度理論

Cornell[2]提出將結構構件的均值與標準差的比值作為該構件的可靠度指標，并以此建立了一次二階矩方法，但是該方法在實際應用中存在一定的缺陷。Hasofer和Lind重新定義了結構可靠度指標的概念，確保了可靠度指標在同一構件不同極限狀態函數下的唯一性，對可靠度理論進行了完善與修正。在數學上，可靠度指標[β]可以定義為如下非線性約束優化問題：

[minβ=d（X*）=i=1nx*i2] ， （1）

[s. t.? ?G（X）=g（x1， x2， …， xn）=0] . （2）

式中：[x]是標準正態空間下的隨機變量，[G（X）]為結構的功能函數，[β] 是結構可靠度指標。結構可靠度的幾何意義是標準正態空間下，結構功能函數上一點到原點的最短距離。對于不服從正態分布的隨機變量，可以使用JC法將其當量正態化。該方法的前提條件是驗算點[x*i] 處[X'i]和[Xi] 的累積分布函數和概率密度函數分別對應相等，由此可以得到正態化之后的變量均值與標準差：

[ux′i=x*i-Φ-1[FXi（x*i）]σx′i] ，? ? ? ? ? ?（3）

[σx′i=?{Φ-1[FXi（x*i）]}fXi（x*i）] .? ? ? ? ? ? ? ?（4）

式中：[Φ（?）] 為標準正態的分布函數，而[?（?）] 為標準正態分布的概率密度函數，[ux′i] 是隨機變量當量正態化后的均值，[σx′i] 是隨機變量當量正態化后的標準差。在得到當量正態化后的變量均值與標準差之后便可以進行可靠度計算。

2? ? CC算法與單純形法計算原理

2.1? ?CC算法

在可靠度計算方法中，經典HL-RF算法由于其概念清晰、計算簡便等優點，被廣泛用于結構可靠度求解，其核心思想是將結構功能函數在第k個迭代點進行一階泰勒展開，并使功能函數在第k+1個迭代點的函數值滿足[g（uk+1）=0] ，可得：

[g（uk）+?g（uk）T（uk+1-uk）=0] .? （5）

令第k+1次迭代點到標準正態空間下原點的距離為[βk+1] ，并取[uk] 點處梯度負方向的單位向量作為迭代選取方向，得：

[uk+1=-βk+1?g（uk）?g（uk）] . （6）

結合式（5），可得：

[βk+1=g（uk）-?g（uk）Tuk?g（uk）] . （7）

式（6）與式（7）合稱為HL-RF算法，其在解決低非線性功能函數可靠度求解問題時計算效率很高，能夠在迭代過程中逐漸靠近收斂點。但是在解決高非線性功能函數時，往往會出現迭代振蕩，甚至不收斂的情況。

為了提高HL-RF算法的收斂性，楊迪雄[7]采用混沌控制學理論對其進行改進，提出了CC算法。該算法引入混沌控制因子對迭代過程中的振蕩情況進行了控制，表達式變為：

[uk+1=uk+λC[F（uk）-uk]] ， （8）

[F（uk）=[?g（uk）]Tuk-g（uk）?g（uk）2?g（uk）] . （9）

式中：[C]代表n×n維對合矩陣，一般情況下取單位矩陣，[λ]是一個常數，代表混沌控制因子。通過上式可以發現，CC算法相較于經典HL-RF算法而言，補充了迭代步長控制計算步驟。先通過HL-RF算法求解出[F（uk）]點，然后以本次迭代點[uk]為基點，將[uk]到[F（uk）]點的方向作為迭代方向，并在該迭代方向上選取一定的步長。如果[λ=0] ，則[uk+1=uk]，無法進行迭代計算;如果[λ=1]，則可得[uk+1=F（uk）]，此時的迭代公式就變成了經典HL-RF算法，所以[λ]的取值為0 ～ 1。為了保證收斂性，[λ]的取值一般設置為較小的常數，導致CC算法的步長較小，收斂速度較慢。如果能使CC算法初始計算點盡可能靠近MPP點，就可以減少計算量，加快算法整體收斂速度。

2.2? ?單純形法

單純形法是一種不將函數梯度信息作為下降方向的算法。該算法在計算初始階段，收斂速度較快，具有一定的計算優勢，但是在貼近極限狀態面之后，計算速度反而開始下降，且單純形法是一種

用于計算無約束問題的算法，根據式（1）、式（2）可知，結構可靠度的計算屬于有約束問題。通過增廣乘子法可以將有約束的可靠度計算問題轉變為無約束優化模型[Mρ]。

[Mρ（X， r， ρ）=i=1n（Xi-μiσi）2+]

[r2j=1n[gj（Xi）]2+j=1nρjgj（Xi] [）].? ? ? ?（10）

式中：[ρ=[ρ1， ρ2， …， ρm]] 為拉格朗日乘子，[r]為罰函數的懲罰因子，[r2j=1n[gj（Xi）]2] 為乘子項，[j=1nρjgj（Xi）] 為懲罰項。

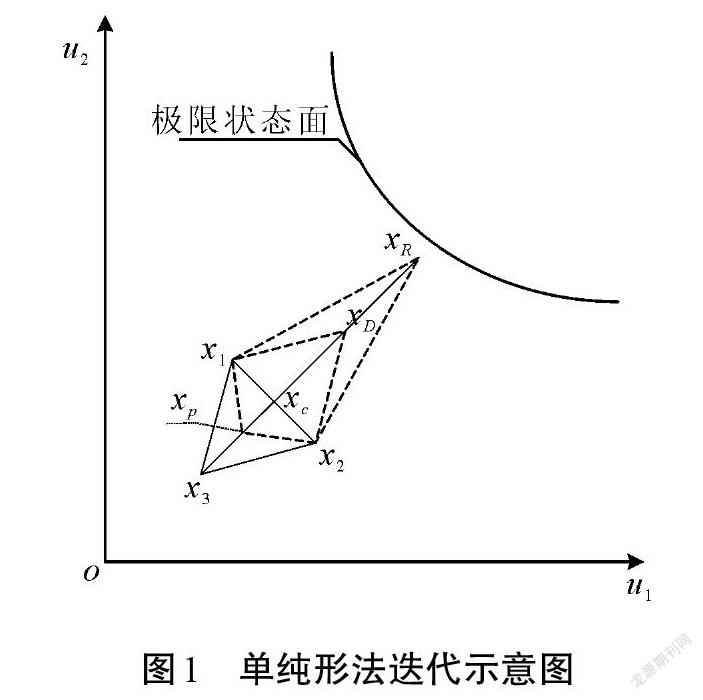
通過增廣乘子算法對功能函數與可靠度指標計算公式進行結合，使得單純形法可以用于可靠度問題的求解。該算法的基本思想是：根據未知變量的個數，選擇n+1個不同的點構成正單純形，分別計算正單純形的n+1個頂點函數值，對比優劣，找到函數值最大的點及函數下降方向，據此來搜索新的點代替最大值點，依次更迭。在迭代點未接近極限狀態面時，[Mρ]優化模型中的懲罰項發揮主要作用，迫使算法向極限狀態面逼近;而當迭代點逼近至極限狀態面附近，懲罰項與乘子項趨近于0，此時可靠度指標的計算公式便可以發揮主要作用，使點通過迭代逐步逼近到最有可能失效點附近，并求得可靠度指標，該算法的迭代示意圖如圖1所示。

圖1中，由x3、[x1]與x2? 3個點共同組成一個單純形，3個點分別為單純形的3個頂點。x3為極差點，xc為反射基點，xD為反射點，xR為延伸點，xp為收縮點。

根據單純形法的基本思想，該理論只適合無約束函數的計算，而增廣乘子法可以將約束優化問題轉化為無約束優化問題，這樣單純形法就可以進行可靠度求解。計算步驟如下所示：

Step? 1? ?將[Mρ]作為目標函數，選取均值點[x11=（x111， x112， …， x11n）T]作為初始點，并將其視為初始單純形的一個頂點，采用式（11）計算正單純形剩余頂點的坐標[19]：

[x12=x11+（d1， d2， d2， …， d2）T，x13=x11+（d2， d1，d2，…， d2）T，x14=x11+（d2， d2， d1，…， d2）T，? ? ? ? ? ? ? ? ? ? ? ? ?? x1n+1=x11+（d2， d2， d2， …， d1）T.]? ? ? ?（11）

其中，[d1=sn2（n+1+n-1）]，[d2=sn2]

[（n+1-1）]，[s]為初始正單純形的邊長。

Step? 2? ?計算[n+1]個正單純形頂點的函數值，并找出其中的最好點[（][x1][）]與最差點[（][x3][）]，然后計算除最差點外剩余點的中心點xc，以此作為基點。

Step? 3? ?以xc點為反射基點，[x3]通過該點進行反射，得到[xD=xc+α（xc-x3）]，其中常數取[α=1][18]，并計算函數值。

Step? 4? ?判斷[Mρ（xD）]的大小。如果[Mρ（xD）≤Mρ（x1）]，則轉至Step? 5;如果[Mρ（x1）<Mρ（xD）<Mρ（x3）]，則由[xD]代替[x3];如果[Mρ（xD）≥Mρ（x3）]，則轉至Step? 6。

Step? 5? ?進行延伸計算，從而得到[xR=xc+γ（xD-xc）]，常取[γ=2][18]，并計算函數值[Mρ（xR）]。如果[Mρ（xR）<Mρ（xD）]，則由[xR]代替[x3];否則由[xD]代替[x3]。

Step? 6? ?[xp=xc+σ（x3-xc）]，常取[σ=0.5][18];如果[Mρ（xp）<Mρ（x3）]，則由[xp]代替[x3]，否則轉至Step? 7。

Step? 7? ?如果經過收縮之后的點仍無法滿足計算要求，則說明該單純形構型需要重新構建，除了最優點外的所有點都沿著本點到最優點的方向移動一半距離，即[xi=x1+δ（xi-x1）]，常取[δ=0.5][18]，轉至Step? 8。

Step? 8? ?判斷算法的收斂情況。如果[1n+1i=1n+1[（Mρ（xi）-Mρ（xc）） ]2 ≤ε]，迭代停止，輸出計算結果;否則[k=k+1]，轉至Step? 2。

單純形法能夠在計算初期迅速將迭代點拉近至極限狀態面附近，但是該算法的缺點是：在迭代點靠近極限狀態面之后會出現計算速度下降、計算結果不準確、誤差較大的情況。

3? ? 基于單純形法改進CC算法

基于單純形法的優點與CC算法存在的不足之處，本文提出基于單純形法改進的CC算法。對于初始迭代點，先使用單純形法進行迭代計算，將點拉近至極限狀態面之后，再采用CC算法進行收斂計算。具體計算流程如圖2所示。

在改進CC算法的計算過程中，最為核心的是如何判斷迭代點已經達到進行CC算法的計算條件。對此，有2種判斷方案可供選擇：第一種是考慮經過單純形法迭代計算之后的點是否已經接近極限狀態面;第二種是考慮單純形的尺寸，即當單純形的尺寸到達一個閾值之后，則轉入CC算法計算。由于單純形法本身并不適用于有約束問題的求解，經過增廣乘子法改進后的單純形法雖然也可以進行可靠度求解計算，并在計算初期迅速將點拉近至極限狀態面，但是該方法會出現各個頂點在接近極限狀態面之前，單純形尺寸已經縮小到算法終止準則，進而導致后續計算無法進行。所以本文選擇第二種方法，將單純形尺寸的閾值作為判斷依據。

4? ? 算例分析

本文算例中混沌控制因子[λ=0.1]，且本文方法

選取均值點作為初始正單純形的一個頂點，通過計算得到的其他正單純形頂點屬于算法中輔助計算的點，并且在后續進行CC算法的計算時并不參與最終的求解計算。所以本文方法迭代圖中只顯示初始均值點在整個算法過程中轉換到標準正態空間U下的迭代路徑。

算例1

假設功能函數形式為：

[Z=x31+x32-4] .? ? ? ? ? ? ? ? ?（12）

本算例中各隨機變量相互獨立且服從正態分布，[x1～N（3.0， 1.0）]和[x2～N（2.9， 1.0）]。求解該算例的可靠度指標。

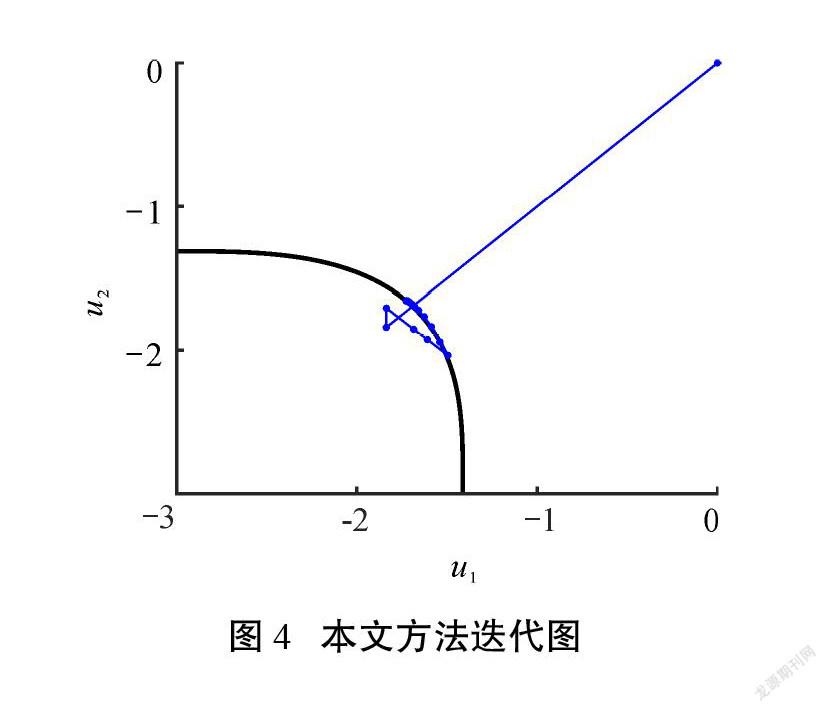
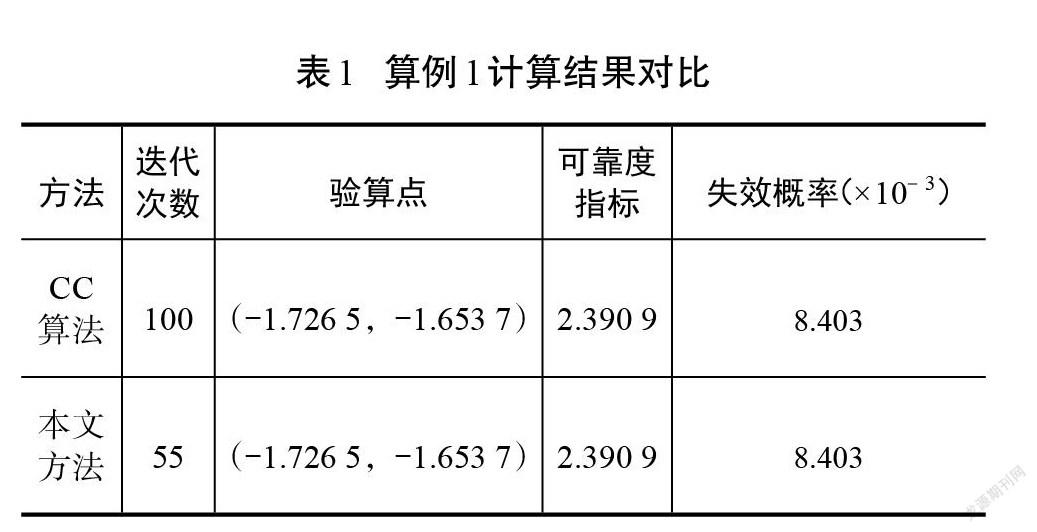
先將各變量轉換到標準正態空間下，然后再進行計算，選擇初始正單純形邊長[s=1]。圖3為CC算法的迭代路徑圖。由圖3可以看到，該功能函數在驗算點處的非線性程度較大，CC算法沿著幾乎呈現線性的迭代路徑以極小的步長向驗算點處進行迭代，最終收斂。圖4為本文方法的迭代路徑圖。從圖4可以看出，該方法很好地融合了單純形法與CC算法的優勢，計算前期能夠迅速逼近至極限狀態面附近，而后逐步向驗算點處收斂。從表1的計算結果來看，本文方法與CC算法并無差別，但迭代次數明顯減少，計算速度得以提升。

算例2

假設功能函數為：

[Z=x41+2x42-20]? .? ? ? ? ? ? ?（13）

其中，各隨機變量相互獨立，為[x1～N（10.0， 5.0）]和[x2～N（10.0， 5.0）]，求解可靠度指標。

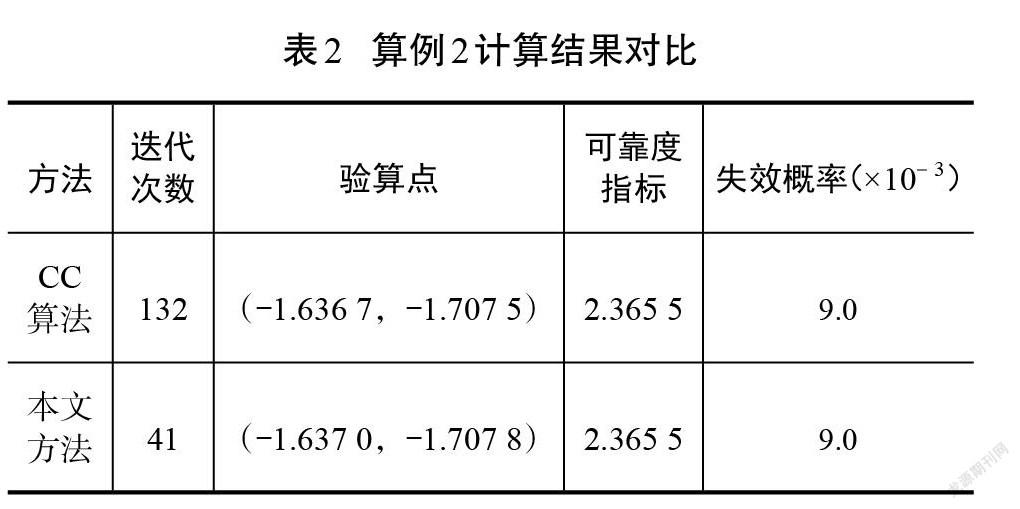
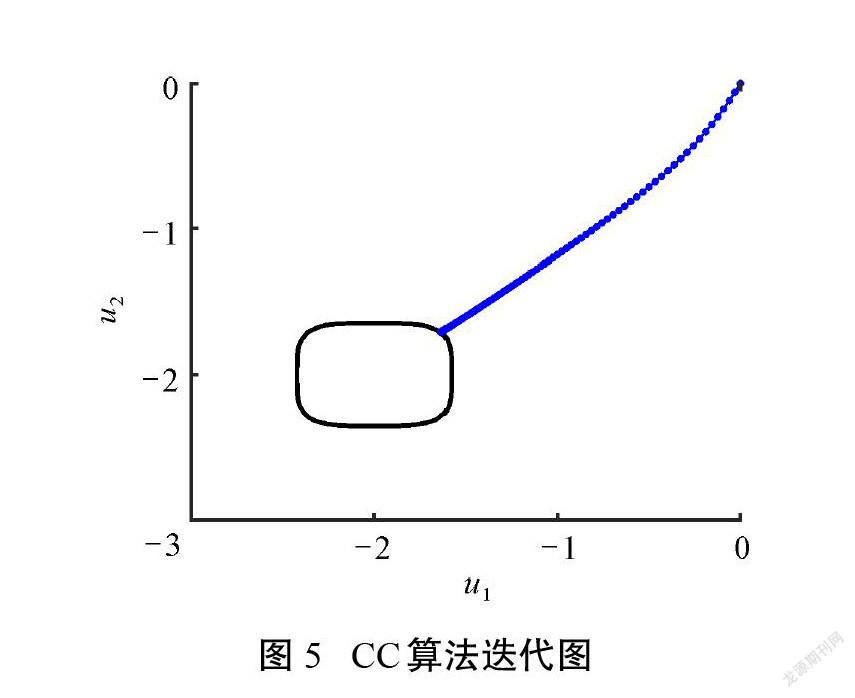
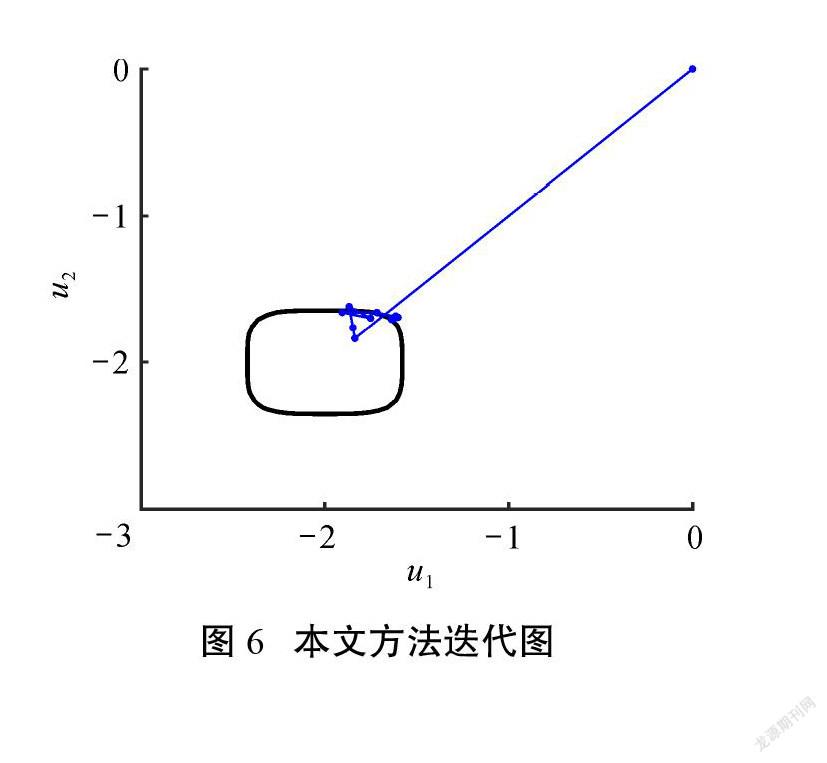
同樣先將功能函數中的變量進行標準正態轉換，而后計算，初始正單純形邊長[s=1]。圖5與圖6分別為CC算法與本文方法的迭代圖，功能函數在驗算點處非線性程度比較大。CC算法沿著一條呈現出順滑曲線的迭代路徑進行迭代，速度相對較慢。本文方法中首次迭代就將點拉近到極限狀態面附近，為后續的可靠度求解計算節省了大量的計算步驟。由表2的計算結果來看，本文方法與CC算法基本一致，且迭代次數更少，效率更高。

算例3

假設極限狀態方程為：

[Z=u3-（u1-1）2-1.5（u2-2）2] .? ? ?（14）

該方程含有3個隨機變量[u1]、[u2]、[u3]，均服從獨立標準正態分布且互不相關，計算可靠度指標。

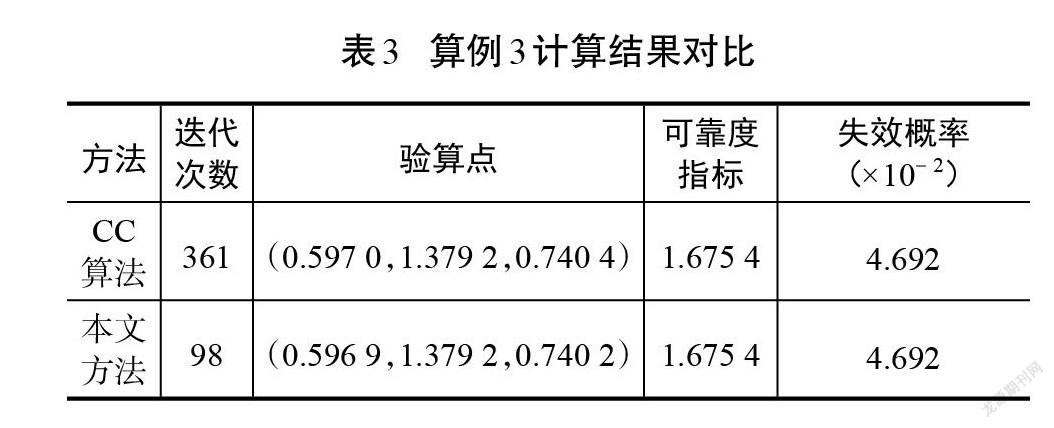
該算例中的隨機變量均服從標準正態分布，不需要進行標準正態轉換。由于該功能函數為三維高非線性，所以縮小初始正單純形邊長為[s=0.1]。迭代路徑圖如圖7和圖8所示。CC算法迭代過程仍然是一條順滑的曲線，但是本文方法在迭代計算初期就迅速將點拉近到極限狀態面附近，有效縮短了后續計算時間，計算結果如表3所示。從表3來看，本文方法與CC算法的計算結果并無太大差別，但迭代次數更少，計算速度更快，說明本文方法具有一定的優勢。

5? ? 結論

當功能函數在驗算點處非線性程度較高時，CC算法迭代路徑往往會呈現一條明晰的曲線，而本文方法則可以依靠單純形的最初幾步迭代計算就能迅速將點拉近到極限狀態面附近，最后通過CC算法進行計算，有效節省了計算時間。通過算例計算表明，本文方法不僅計算結果與CC算法基本一致，而且還減少了迭代次數，迭代次數僅為 CC算法的1/4～1/2，證明了本文方法兼具準確性與計算速度。

參考文獻

[1]? ? FREUDENTHAL? A? M. The safety of structures[J].Tranactions of the American Society of Civil Engineers， 1947， 112（1）：125-159.

[2]? ? ?CORNELL? C? A. A probability-based structural code[J].Journal of American Concrete Institute，1969， 66（12）：974-985.

[3]? ? ?HASOFER? A? M，LIND? N? C. Exact and invariant second moment code format[J].Journal of Engineering Mechanics，1974，100（1）：111-121.

[4]? ? ?RACKWITZ? ?R，FLESSLER? B. Structural reliability under combined random load sequences[J]. Computers and Structures， 1978， 9（5）：489-494.

[5]? ? ?LIU? ?P? ?L. Optimization algorithms for structural reliability[J]. Structural Safety， 1991， 9（3）：161-177.

[6]? ? ?ZHANG? Y， KIUREGHIAN A D. Two improved algorithms for reliability analysis[M]//Reliability and Optimization of Structural Systems. Boston：Springer，1995：297-304.

[7]? ? ?楊迪雄. 結構可靠度分析FORM迭代算法的混沌控制[J]. 力學學報， 2007，39（5）：647-654.

[8]? ? ?MENG? Z， LI? G， YANG? D? X，et al. A new directional stability transformation method of chaos control for first order reliability analysis[J]. Structural and Multidisciplinary Optimization， 2017， 55（2）：601-612.

[9]? ? ?韋春妙， 龐建華， 黃李韋， 等. 新Armijo線搜索下的PRP共軛梯度法及其收斂性分析[J]. 廣西科技大學學報， 2019，30（2）：107-114.

[10]? ?李彬， 李剛. 基于Armijo準則的自適應穩定轉換法[J]. 計算力學學報， 2018， 35（4）：399-407.

[11]? ?李彬， 郝鵬， 孟增， 等. 基于改進自適應混沌控制的逆可靠度分析方法[J]. 應用數學和力學， 2017， 38（9）：979-987.

[12]? ?亢戰， 羅陽軍. 計算結構可靠度指標的修正迭代算法[J]. 工程力學， 2008， 25（11）：20-26.

[13]? ?貢金鑫. 結構可靠指標求解的一種新的迭代方法[J].計算結構力學及其應用， 1995（3）：369-373.

[14]? ?吳狄， 關鼎. 一種結構可靠性指標的搜索方法[J]. 計算力學學報， 2005，22（6）：788-791.

[15]? ?王林軍， 王錟， 杜義賢， 等. 一種基于外罰函數法的結構可靠性分析方法[J]. 三峽大學學報（自然科學版）， 2019， 41（1）：92-96.

[16]? ?高翔， 王林軍， 杜義賢. 采用增廣乘子法和模擬退火法的結構可靠性分析[J]. 西安交通大學學報， 2019， 53（7）：144-152.

[17]? ?許家赫， 陳岳坪. 改進粒子群算法與fmincon函數混合尋優的平面度、垂直度誤差評定[J]. 廣西科技大學學報， 2019， 30（4）：105-109.

[18]? ?劉惟信. 機械最優化設計[M]. 2版. 北京：清華大學出版社， 1994.

[19]? ?康哲民. 基于響應面法的結構可靠性分析及應用[D]. 柳州：廣西科技大學， 2019.

Improved chaos control algorithm based on simplex method

XIA Yu， TANG Feng， YU Yingye

（ School of Civil Engineering and Architecture， Guangxi University of Science and Technology，

Liuzhou? 545006，? China）

Abstract： Chaos control（CC） algorithm has superior robustness in solving structural reliability problems， but the strict restriction for step size makes calculation speed low. Simplex method is an algorithm that does not take the gradient direction as the optimization direction. The initial calculation speed of the simplex method is fast. And it can approach to the limit state surface quickly at the beginning of calculation， after that， the calculation speed decreases obviously and the error of calculation results is large. In this paper， an improved chaos control algorithm based on simplex method is proposed. Firstly， the nonlinear equation constraint problem in reliability calculation is transformed into unconstrained problem by the augmented multiplier method.? Then， the simplex method is used for initial iterative calculation.? Finally， CC algorithm is used for convergence calculation.? The numerical results show that the proposed algorithm can solve the reliability problem of high nonlinear function effectively and has the advantages of both algorithms. Compared with the chaos control algorithm， the proposed algorithm improves the calculation efficiency.

Key words： structure reliability; chaos control algorithm; simplex method; reliability calculation; calculation efficiency

（ 責任編輯：羅小芬）