高階思維視角下的幾何定理教學
——以“三角形一邊的平行線性質定理的推論”為例

200233 上海市世界外國語中學 梁 舒

《義務教育數學課程標準》(2011年版)指出，教學活動應當培養學生運用數學的思維方式進行思考，增強發現和提出問題的能力，分析和解決問題的能力

.

按照布魯姆的認知目標分類(此處看作思維目標)，教學目標依據認知復雜程度由低到高分為識記、理解、應用、分析、評價、創造六個層次，其中后三層(分析、評價、創造)被稱為高階思維能力

.

高階思維體現了時代對人才素質提出的新要求，也是適應時代發展的關鍵能力

.

因此，在數學教學中應注重滲透數學思想和方法，培養學生的思維，尤其是分析、評價和創造層次的高階思維

.

學生高階思維培養的主要場所是數學課堂

.

因此，教師在設計引入、概念形成、例題處理以及小結的各個環節上如何設計思維任務，啟發學生的高階思維顯得尤為重要

.

筆者以“三角形一邊的平行線性質定理的推論”為例，闡述對高階思維視角下課堂實施的見解

.

一、 教學環節

(一)情境導入

原題

一臺幻燈片投影儀被安裝在距離屏幕4米處，幻燈片距離投影儀16毫米(如圖1所示)，

AD

∥

BC

，如果幻燈片是一張長為22毫米、寬為16毫米的圖片，求圖片投影在屏幕上圖像的長和寬

.

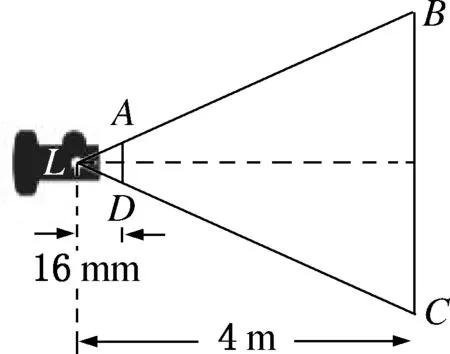
圖1

師：題目中有哪些已知信息？三角形一邊的平行線性質定理的條件和結論分別是什么？(引導學生對題目進行分析，嘗試將其與已學知識建立聯系)

生：已知

AD

∥

BC

以及一些線段的長度

.

條件是有一條平行于三角形一邊的直線截其他兩邊所在的直線，結論是截得的對應線段成比例

.

圖形語言表述如圖所示，其中圖2-1、圖2-2為A字型圖形，圖2-3為X型圖形.

圖2-1圖2-2

圖2-3圖3

生：題目符合A字型

.

(定理轉換為圖形語言后，學生很容易與A字型聯系起來)

師：題目滿足性質定理的條件，運用性質定理能否求得圖片投影在屏幕上圖像的長和寬，能否解決該問題？(引導學生將題目的所求與性質定理的結論進行對比，發現性質定理的局限)

生：不能

.

如圖3，將問題抽象成A字型后，圖像的長是圖中

BC

的長，

BC

不在三角形被截的兩邊所在的直線上，性質定理的結論中沒有涉及這種情況

.

學生對比后發現雖然題目中的圖形符合A字型，也滿足相關條件，但運用性質定理的結論卻無法解決該問題，進而產生了認知沖突

.

(二)探究三角形一邊的平行線性質定理推論

師：在性質定理的結論中，有關的比例線段分別在三角形兩邊所在的直線上，圖形中線段

DE

雖不在三角形被截的兩邊上，但是它和圖形中其他線段之間是否存在比例關系？(向學生指明思考的方向)師：先考慮

D

和

E

分別是三角形兩邊中點的特殊情況

.

(學生已學習中位線定理，較容易解決此問題)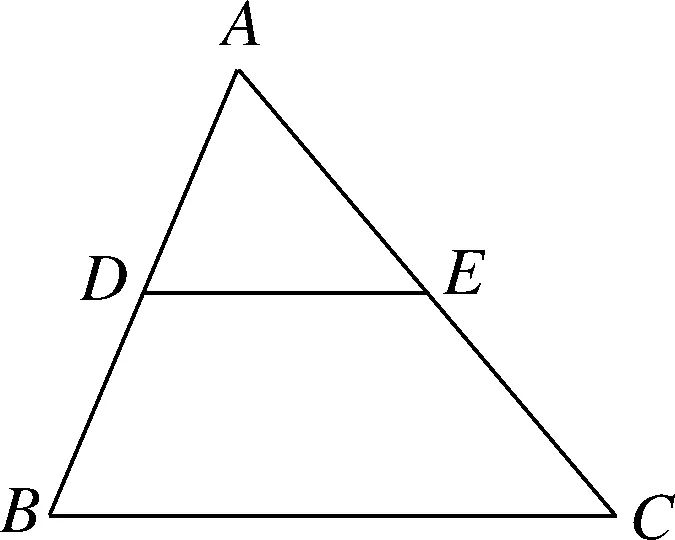

圖4

問題1

如圖4，如果點

D

，

E

分別在△

ABC

的邊

AB

，

AC

上，且

D

，

E

是邊

AB

，

AC

的中點，

DE

∥

BC

，那么成立嗎?師：再考慮

D

和

E

是三角形兩邊上任意一點的一般情況

.

(引導學生對一般情況進行分析思考，培養學生分析問題的能力)

問題2

問題1中點

D

和點

E

位置改變時，圖形存在哪幾種情況？根據“點的位置移動”，學生可能畫出的圖形如圖5-1—圖5-9所示

.

圖5-1圖5-2

圖5-3圖5-4

圖5-5圖5-6

圖5-7圖5-8

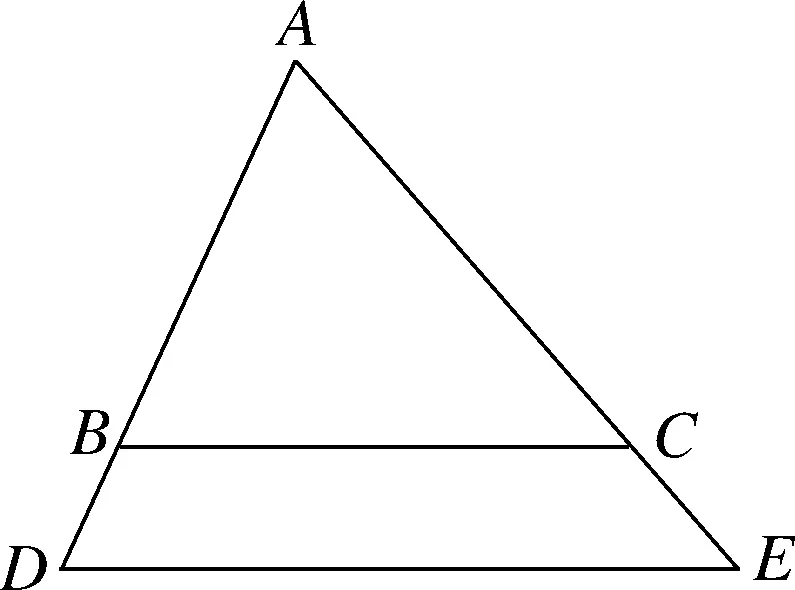
圖5-9

師:大家畫出的圖形與問題1中的圖形相比有什么異同？是否可以按某種標準將上述圖形進行分類呢？(引導學生將情況分類，發現性質定理推論的條件)

生：按照

DE

是否與

BC

平行進行分類

.

結合圖形和已學性質定理，學生能較為容易地對圖形進行分類，如下所示

.

問題3

在圖5-3和圖5-6兩種情況下，是否仍然成立?如果成立，請給出證明

.

請大家分小組討論，之后每組選出一位同學分享

.

師：

D

，

E

分別在△

ABC

的邊

AB

，

AC

上時，如圖5-3的情況如何證明？

圖6-1圖6-2

方法1：

過

D

作

DF

∥

AC

交邊

BC

于點

F

(如圖6-1)

.

方法2：

延長

DE

到

G

，使

DG

=

BC

，聯結

CG

(如圖6-2)

.

學生在證明中位線定理時已經運用過方法2，故學生較易得出此方法

.

對于方法1，學生之前沒有構造此類輔助線的經歷，可能需要教師引導

.

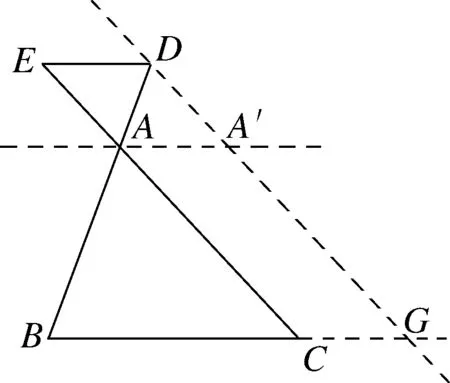
圖7

師：

D

，

E

在

AB

，

AC

延長線上時，圖5-6情況下的X型如何證明呢？學生在證明性質定理的時候證明過X型，故可思考得出通過構造輔助線將X型轉化為A字型來解決(如圖7所示)

.

師：從上面的證明中，你能得到什么結論？請一組同學分享，其他組補充

.

生：平行于三角形一邊的直線截其他兩邊所在的直線，截得的三角形的三邊與原來三角形的三邊對應成比例

.

學生類比性質定理的描述，能較為準確地總結得出該性質定理的推論

.

問題4

比較上述證明方法，分析解題思路

.

師：在A字型的證明中運用了以下兩種方法

.

(引導學生分析、評價解題思路，培養學生分析、評價的能力)

方法1：

運用三角形一邊的平行線的性質定理，該定理從一條平行于三角形一邊的直線出發，結論中的比例線段都在三角形的被截兩邊所在的直線上，因此，要運用該定理，需要將

DE

平移到三角形被截的邊上去

.

故需增添輔助線

.

方法2：

考慮構造X型

.

或者從另一個角度思考，三角形中位線定理的證明是通過將三角形旋轉180°，構造平行四邊形，本題借鑒該思路

.

建立未知與已知之間的聯系，將未知轉化為已知來解決

.

可能選擇方法2的學生較多，因為之前已經習得此方法，而方法1運用性質定理解決，為今后解決其他問題提供思路

.

師：根據相似三角形的定義，圖5-3、圖5-6、圖5-9中△

ABC

和△

DEF

是否相似？(引導學生考慮相似問題，為后續相似三角形判定的教學埋下伏筆)生：將△

DEF

看作是△

ABC

放大(或縮小)得來的，所以△

ABC

和△

DEF

相似

.

學生根據相似三角形的定義，較易得出結論

.

師：那么，它們是否符合相似多邊形的性質呢？

生：根據平行線的性質和已證得的三角形一邊的平行線性質定理的推論，可知△

ABC

和△

DEF

三個角對應相等，三邊對應成比例，因此，△

ABC

和△

DEF

符合相似多邊形的性質

.

(強化相似性的性質，為后續相似三角形的判定打下基礎)

(三)三角形一邊的平行線性質定理推論的應用

1

.

在幾何問題中的應用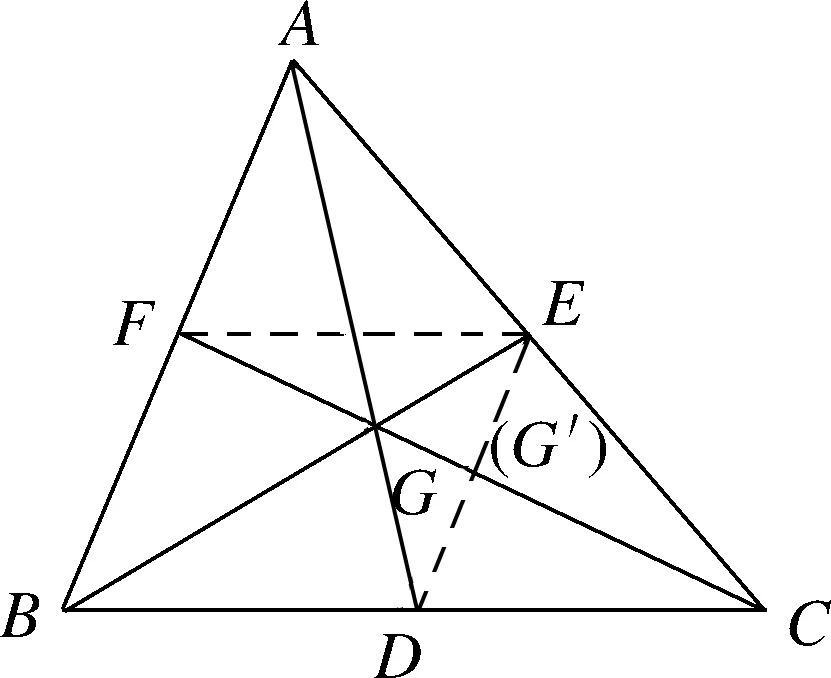

圖8

例1

已知

BE

，

CF

是△

ABC

的中線，交于點

G.

求證：對學生來說，此題運用三角形的中位線定理可以容易地證明(如圖8所示，

AD

也是△

ABC

的中線)

.

師：請大家分別用文字語言和符號語言表述這一性質

.

(引導學生將符號語言與文字語言相互轉化)學生的表述如表1所示

.

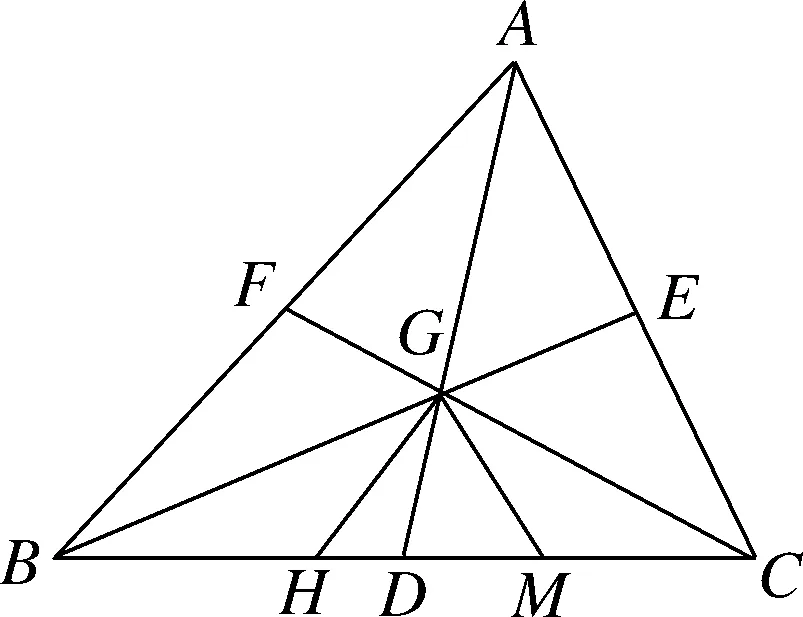
圖9

練習1

如圖9，在上述例題的基礎上再次改變條件，增加兩條平行線，過

G

分別作

GH

∥

AB

，

GM

∥

AC

,分別交邊

BC

于點

H

，

M.

求證：通過變式練習，學生對比條件和結論的異同，找到相似之處作為突破口，增強分析問題的能力

.

2

.

在實際問題中的應用

例2

(例2為上文“情境導入”中的原題，此處略)

解：

如圖1，因為

AD

∥

BC

，所以所以圖像的寬=4米，圖像的長=5

.

5米

.

學生學習性質定理的推論后再解決“情境導入”中的原題，問題迎刃而解

.

師：性質定理的推論不僅包含了原定理的一些結論，還拓展了原定理的結論

.

在實際生活中，還有哪些問題可以運用三角形一邊平行線性質定理的推論基本圖形A字型來解決？(引導學生運用已學知識反思實際生活的問題)

表1

文字語言符號語言三角形三條中線的交點叫做三角形的重心.三角形的重心到一個頂點的距離,等于它到這個頂點對邊中點距離的兩倍AG=2GDCG=2GFBG=2GEGD=12AGGD=13ADAG=23ADAG∶GD=2∶1GD∶AD=1∶3AG∶AD=2∶3

生：運用自己的影子來測量路燈的高度、建筑物的高度或河的寬度等

.

師：請大家根據上述例子及性質定理的基本圖形(A字型圖形和X型圖形)自主編題，要求解題過程用到三角形一邊平行線性質定理的推論，并在小組內分享自己的題目，最后每個小組選一個方案進行班級分享

.

該環節中，學生需要思考實際問題并將其與性質定理的推論結合，而自主編題要求學生在分析后對問題進行加工、再創造，難度較大，故采用小組的形式，目的是培養學生的分析、創造等高階思維能力

.

(四)小結

師：本節課我們學習了三角形一邊的平行線性質定理推論，對比三角形一邊的平行線性質定理與性質定理推論的條件和結論，它們有何異同？

師：回憶推論導出的過程，我們經歷了怎樣的過程？是從哪種情況開始證明的？(引導學生回憶，分析證明過程)

生：從

D

，

E

是三角形的兩邊的中點出發，接下來考慮點

D

和

E

位置移動的一般情況，在一般情況中分別討論

D

和

E

是三角形兩邊上任意一點和

D

，

E

分別是三角形兩邊延長線上的情況

.

師：從

D

，

E

是三角形兩邊的中點的特殊情況出發，再引發

D

，

E

在三角形兩邊上任意位置的一般情況的討論與證明，從猜想到嚴格的演繹推理論證，在這個過程中我們體會了從特殊到一般以及類比歸納的數學思想

.

(進行數學思想的滲透)在考慮點

D

和

E

的位置移動的一般情況時，學生獨立分析思考，畫出不同的圖形，體會用運動變化的觀點看待問題，然后對不同圖形進行分類，最后分情況證明結論

.

在分情況證明中將幾何圖形分解得到基本圖形，再根據基本圖形的性質解決問題，學生體會分類討論及化歸的數學思想

.

在探索推論的過程中，先由特殊情況(

D

，

E

是三角形兩邊中點)猜想哪幾種圖形結論成立，隨后通過證明驗證之前的猜想，歸納總結三角形一邊的平行線性質定理推論，并對證明方法進行分析評估，體會幾何演繹的思想和邏輯推理的方法

.

這也是探究性研究經歷的一般過程

.

二、 分析與思考

(一)以實際問題導入引發思考

本節課以實際問題導入，問題滿足三角形一邊的平行線性質定理的條件，但是運用性質定理卻不能解決，引發學生的認知沖突，引起學生的求知欲

.

學生體會到問題的起源，找到新知識與原有知識的聯系

.

同時復習舊知，并歸類基本圖形，為性質定理推論的導出和證明提供途徑，便于將已有的知識和經驗遷移到新的知識及研究過程，為本節課的研究奠定基礎

.

(二)推導過程中培養學生分析、評價的高階思維能力

本節課在性質定理的推導過程中著重培養學生分析、評價問題的能力

.

引導學生抓住問題中關鍵信息“點的位置”，以此為突破口進行分析，引導學生用運動變化的觀點看待問題，變化出更多樣的圖形，嘗試綜合全面地思考問題

.

在獨立畫圖、分析思考的過程中，學生分析出可能存在的圖形，教師引導學生將圖形進行分類，分別考察圖形的可行性，這也是分析問題必須具備的技能

.

在推導完成后，引導學生思考、評價不同的證明過程，提升學生分析和評價能力，學生經歷“猜想—驗證—分析論證—評估—結論決策”這一探究性研究的完整過程

.

由猜想到驗證，思維反復調整

.

最后，學生體驗歸納結論，從自己的語言提煉成書面語言的過程，思維不斷完善，有利于思維的整合，培養思維的嚴密性

.

(三)在應用性質定理的過程中培養學生分析、創造的高階思維能力

在性質定理的運用環節中，著重培養學生的分析、創造的思維能力

.

在性質定理應用中提出的實際問題正是開頭情境導入環節的問題

.

在情境導入環節引導學生嘗試從數學角度分析實際問題，抽象出數學圖形，引發認知沖突，在應用性質定理的推論這一環節，學生再次分析問題，結合已學知識解決該問題，學生分析問題的能力得到培養

.

在關于性質定理應用的幾何問題中，引導學生分析題目的條件和結論，讓學生經歷再創造的過程，發現三角形重心的性質

.

在自主編題環節中，學生具有更大的主動性，這一環節是學生對問題分析再創造的過程

.

學生需要思考身邊的實際問題，運用已學數學知識分析實際問題，并創造性地解決實際問題

.

這一過程也能培養學生分析和創造的高階能力，并讓學生體會數學來源于生活、服務于生活

.

(四)課堂小結，反思思維過程，延伸高階思維

課堂小結從數學知識、方法和思想方面概括本節課的內容

.

引導學生在知識方面從模糊走向清晰，從片面到全面

.

注重數學思想方法的滲透，提高學生分析評價的能力

.

反思的過程是對自身研究問題的思維過程，是對結果和思維方法等進行再認識、再評價的過程，教師培養學生的批判性思維，使思維變得越來越成熟

.