構造向量求數列的和
2022-07-08 00:56:18215600江蘇省梁豐高級中學
中學數學雜志 2022年4期
215600 江蘇省梁豐高級中學
江蘇省張家港市羅建宇名教師工作室 趙穎穎
向量是溝通幾何與代數的橋梁,是進一步學習和研究其他數學領域問題的基礎[1].在中學教學實踐中,向量常作為工具來解決幾何問題,也能解決一些代數問題,向量的運用多見于等式、不等式、函數等問題(參見文[2]-文[9]).筆者構造向量求幾類典型數列的和,作為向量在解決代數問題中的補充,用以倡導在高中數學知識間進行相互論證,發展數學學力.
一、 構造向量推導等差數列前n項和公式
問題1設數列{an}是公差為d的等差數列,求數列{an}的前n項和.
解析:當d=0時,易得.下面推導當d≠0時的求和公式.
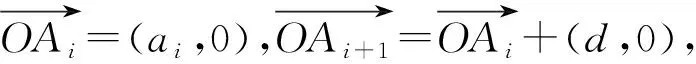
評注:從向量的視角看,等差數列對應向量的加減法運算,問題1的解決是在構造向量的基礎上,結合向量的模的計算得以推導等差數列前n項和公式.類似地,利用上述對向量的模的計算方法,可以求數列{nm}(m∈N*)的前n項和,簡析如下.

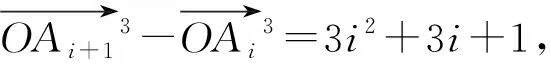
二、 構造向量推導等比數列前n項和公式
問題2設數列{an}是公比為q的等差數列,求數列{an}的前n項和.
解析:當q=1時,易得.下面推導當q≠1時的求和公式.
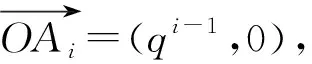
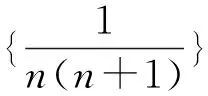
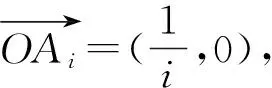
三、 構造向量求“等差×等比”數列前n項和
問題3設數列{an}是公差為d的等差數列,數列{bn}是公比為q的等比數列,求數列{an·bn}的前n項和.
解析:同上,這里只需解析當q≠1時的求和.

評注:問題3的解決常用經典的“錯位相減法”求和,這里是在構造向量的基礎上綜合運用有關向量的線性表示,結合向量數量積運算求得“等差×等比”數列的前n項和公式.

