304奧氏體不銹鋼厚板斷后伸長率的換算
張 華,陸海兵
(寶山鋼鐵股份有限公司制造管理部,上海 201900)
拉伸試驗的斷后伸長率是判斷金屬材料塑性的重要指標。現行拉伸試驗標準(如GB/T 228.1、ASTMA370和ISO 6892.1等)對不同產品類型及厚度規格的材料規定有多種試樣尺寸和形狀類型的拉伸試樣,由于斷后伸長率與拉伸試樣的形狀、橫截面積和標距等因素有較大關系,容易造成不同試樣的斷后伸長率無法直接比較,給實驗室性能判斷和用戶使用材料帶來諸多不利。為解決此問題,Oliver在1928年發表了一篇論文,提出了用于不同原始標距和不同試樣橫截面積試樣的斷后伸長率的換算公式,稱為Oliver公式,核心是需要擬合出公式中的常數n,其值近似材料常數。現行的伸長率換算方法標準都以該公式為基礎,常用的有:GB/T 17600.1—1998、GB/T 17600.2—1998、ISO 2566—2:1984等。對于普通低碳鋼,標準GB/T 17600.1推薦的常數n為0.4,寶鋼檢化驗中心相關實驗室通過多年的數據積累,證實了該值在普通低碳鋼上有很好的適用性。對于不銹鋼產品,斷后伸長率換算標準為GB/T 17600.2—1998,其規定:伸長率換算適用于寬厚比小于20、比例系數小于25以及抗拉強度在450~750 MPa之間的固溶態奧氏體鋼,推薦的擬合常數n為0.127。文獻[1-5]對低碳鋼、固溶態奧氏體不銹鋼的伸長率換算公式采用理論分析或相關性分析發現:不同的試樣寬厚比、比例系數情況下,擬合得到的Oliver相關參數與標準的推薦值存在不完全吻合的現象。目前針對不銹鋼的伸長率換算研究主要集中在薄板產品,對于奧氏體不銹鋼厚板(特別是厚度大于15 mm)的研究較少,因此有必要開展相關研究,以期得到準確的斷后伸長率換算公式。
1 試驗部分
1.1 試驗原理
基于Oliver公式,建立斷后伸長率的換算關系,由某一已知標距尺寸的實測斷后伸長率A換算到另一標距尺寸的斷后伸長率Ar,基本換算如式(1):
Ar=(K/Kr)nA
(1)
式中:K和Kr分別為A和Ar對應的比例系數。
Oliver描述斷后伸長率的規律表達式見式(2):
(2)
式(2)兩邊取對數后為式(3):
(3)
式中:n和σ為近似材料常數;S0為試樣原始橫截面積;L0為試樣原始標距。
1.2 試驗條件
選擇典型的固溶態304奧氏體不銹鋼作為研究對象,鋼板厚度規格分別為18、20、22、28和32 mm。采用全厚度矩形橫截面試樣,平行段寬度為40 mm,平行長度為230 mm,用標點機在試樣平行長度范圍打上間隔10 mm的標距標記。試樣首先按照GB/T228.1—2010進行室溫拉伸試驗,保證試樣的斷裂位置位于平行段長度的中心,依次選擇30、40……190、200 mm作為試樣原始標距,分別測量對應的斷后標距,再計算出相應的斷后伸長率,利用Origin軟件對試驗數據進行回歸分析。
2 試驗結果和討論
2.1 拉伸斷口形貌
上述不銹鋼拉伸斷樣的宏觀斷口照片如圖1所示。觀察宏觀斷口發現:試樣斷裂面的側面與試樣中軸線的夾角均小于70°,斷面呈現灰黑色纖維狀形貌,屬于典型的剪切斷裂特征。

圖1 拉伸斷樣宏觀斷口Fig.1 Macro fracture of tensile specimen
2.2 試樣尺寸參數和力學性能
表1為試樣尺寸參數和力學性能。
從表1可知:5種厚度規格試樣的拉伸屈服強度范圍為222~243 MPa,抗拉強度范圍為622~644 MPa,材料總體力學性能差異不大。試樣寬厚比的范圍為1.25~2.22,比例系數均小于8。GB/T 17600.2—1998規定:寬厚比<20、比例系數<25、抗拉強度<750 MPa的不銹鋼試樣適用標準推薦的Oliver公式。通過對比表1中數據,以上試樣均滿足標準的規定。
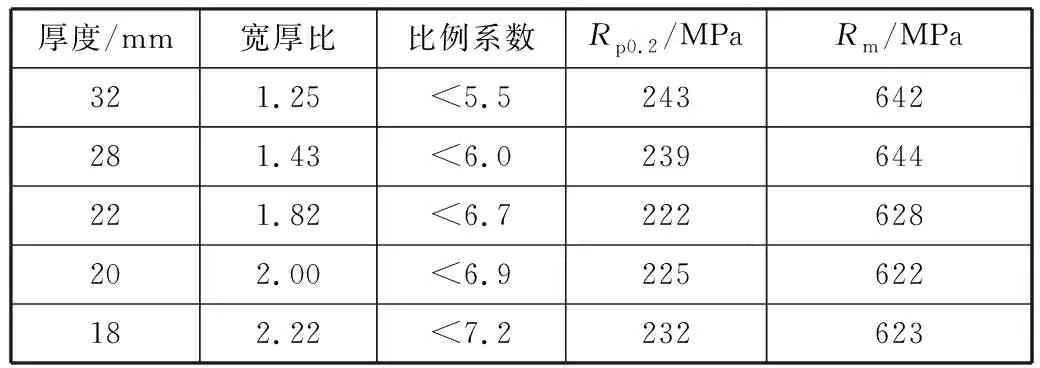
表1 試樣尺寸參數和力學性能Table 1 Dimensions and mechanical properties
2.3 擬合Oliver常數n
根據文獻[1],當拉伸原始標距處于斷裂位置的頸縮區時,測得的斷后伸長率波動較大,對于Oliver公式中的常數n的準確性影響很大。本次試驗中拉伸斷口的頸縮區的范圍約為30 mm,因此選擇從30 mm作為原始標距的起點,標距范圍為30~200 mm,測得的斷后伸長率與原始標距的關系見圖2。
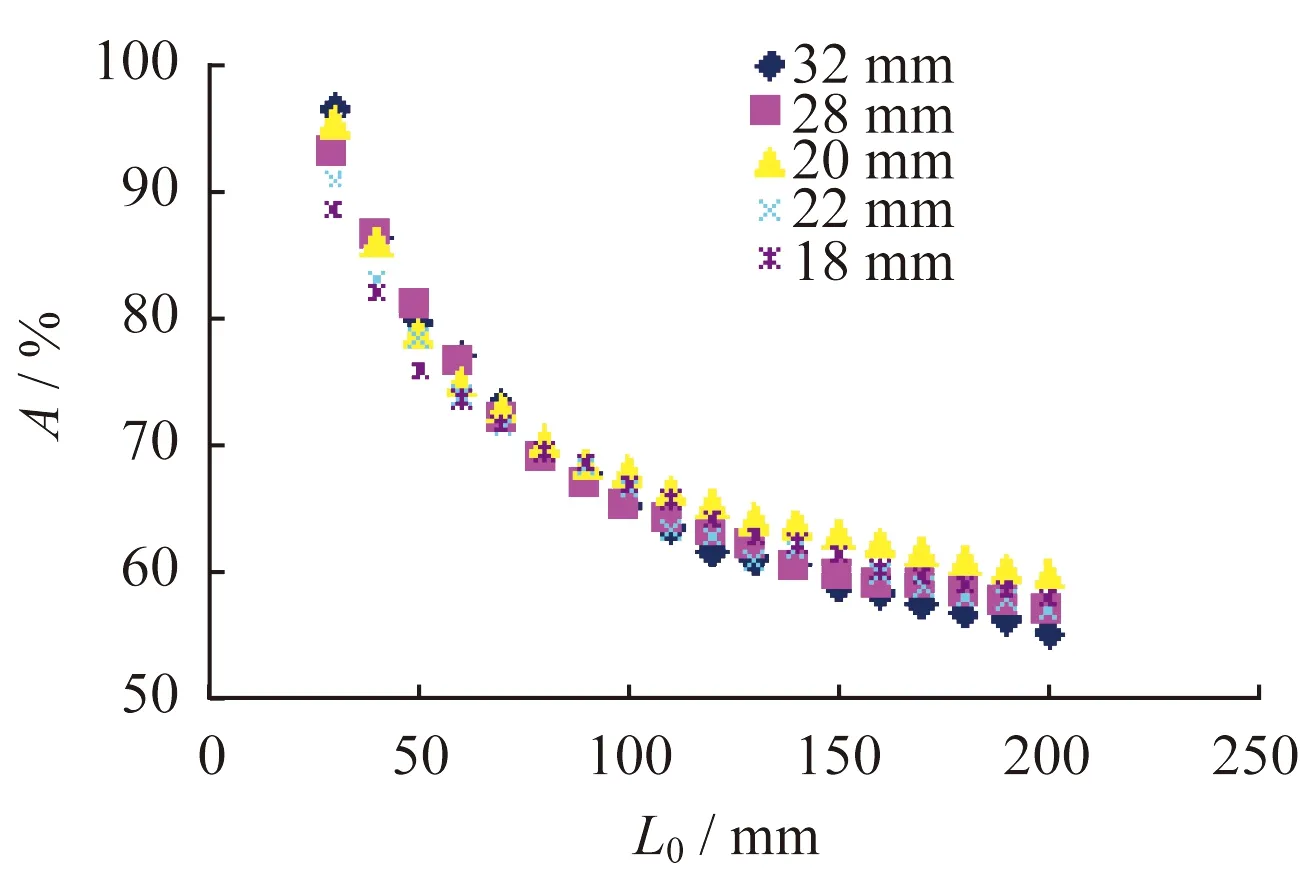
圖2 斷后伸長率與原始標距的關系圖Fig.2 The relationship between A and L0

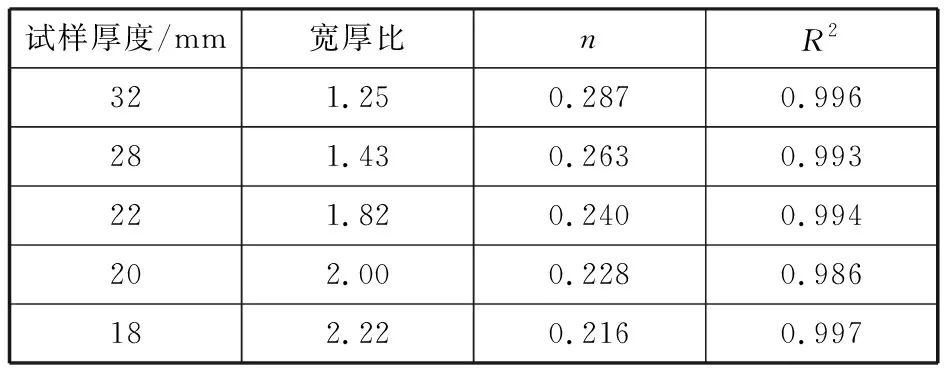
表2 n和R2的擬合結果Table 2 Fitting results of n and R2
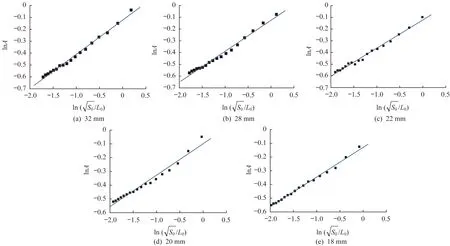
圖3 不同厚度試樣的擬合曲線Fig.3 Fitting curves of different thickness specimens
2.4 影響n值的因素分析
從表1的試樣力學性能可知:上述不同厚度規格試樣的抗拉強度性能不存在明顯差異,抗拉強度性能均符合標準GB/T 17600.2規定的Oliver公式適用范圍,所以本次試驗中試樣強度性能對n值的影響可忽略。表2的結果顯示:試樣厚度規格與n的擬合結果存在明顯的正相關,隨著試樣厚度從18 mm增加到32 mm,n值從0.216增加到0.287,該趨勢也與圖2顯示的斷后伸長率隨著試樣厚度增加而降幅加快的趨勢一致。擬合結果與標準GB/T17600.2和ISO 2500—2的推薦值(n=0.127)存在一定的差異,與文獻[5]的擬合結果相近(n=0.199)。
此外試樣斷裂位置對n值也有較大影響,通過試驗3根厚度18mm的平行試樣,試樣斷裂位置分別位于平行段標距的1/2、1/3和1/4,按前文2.3所述的方法得到各自的擬合常數n,結果見表3。結果顯示,當斷裂位置位于平行段標距1/2時,n值最小,約為0.216;隨著斷裂位置偏移至1/3和1/4,n值也逐漸變為0.222和0.256。因此,試樣斷裂位置越接近平行段標距的中心時,擬合的n值越小。
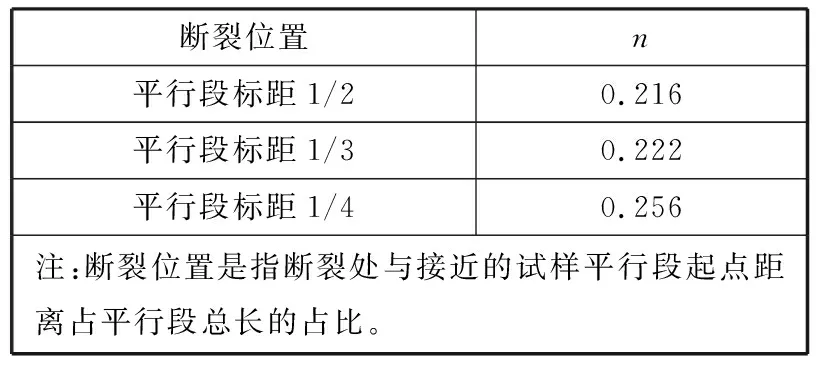
表3 厚度18 mm的平行試樣不同斷裂位置的n值Table 3 n values of different fracture positions of 18 mm thick specimens
2.5 Oliver公式效果驗證
挑選18、22和28 mm三種厚度規格試樣,采用上述擬合的n值和標準推薦的n值分別換算出不同原始標距時的斷后伸長率(表4),換算時參照180 mm原始標距的斷后伸長率A180 mm,原始標距分別為50、80、100 mm和短比例標距。通過與實測斷后伸長率的比較可知:不同n值的換算結果差異較大,按標準推薦值(n=0.127)進行換算時,斷后伸長率換算值與實測值相差較大,標距越小誤差越大,厚度規格越大誤差也越大,其中厚度28 mm試樣換算50 mm標距時的斷后伸長率與實測值相差達到15.9%,平均差值也達到6.2%;采用擬合的n值時,換算值與實測值的誤差明顯減小,最大差值僅為3%。因此,采用本次試驗得到的n值換算斷后伸長率效果較好。
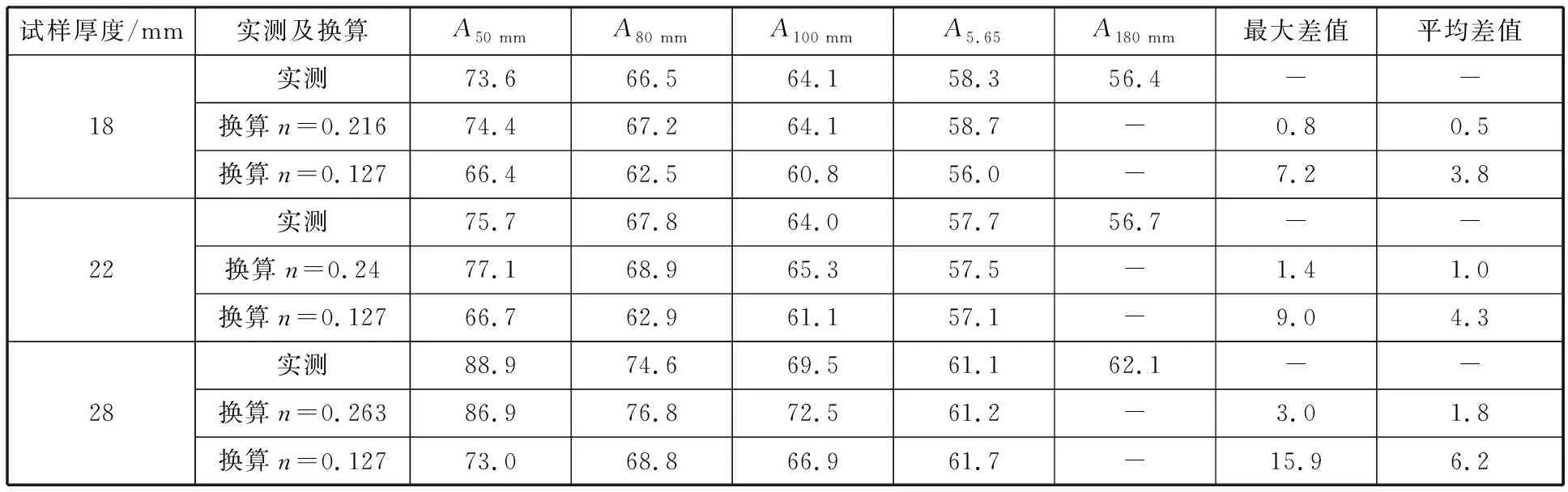
表4 不同n值時實測值與換算值的比較Table 4 Comparison of measured value and converted value with different n value %
3 結論
(1) 通過研究得到了適用于304不銹鋼厚板產品的拉伸斷后伸長率換算Oliver公式,其常數n的取值范圍在0.21~0.29之間,采用標準GB/T 17600.2推薦的n值(0.127)換算的斷后伸長率與實測值的相差較大。對于此類厚度規格較大的304不銹鋼產品宜采用更高的n值。
(2) 本試驗中擬合常數n值大小與以下因素相關:n值隨試樣厚度的增加而增大;n值與試樣的斷裂位置有關,試樣斷裂位置越偏離試樣平行段中心位置,擬合的n值越大,越靠近平行段中心n值越小。因此,在使用Oliver公式進行不銹鋼斷后伸長率換算時應當綜合考慮試樣形狀、規格、斷裂位置等因素,根據實際產品特性和試驗條件尋找更適用的擬合常數n。

