基于靜力簡化的斜風(fēng)作用下橋上車輛行駛安全研究

[摘? 要]：近年來，風(fēng)致行車事故較多。文章以橋上行駛車輛為研究對象，首先采用CFD數(shù)值模擬的方法計算車輛氣動力，然后基于靜力簡化的方法，計算得到車輛的行車臨界風(fēng)速，可以較快地對車輛的行駛安全進行評價。研究結(jié)果表明：隨著風(fēng)偏角增大，車輛的側(cè)力系數(shù)、升力系數(shù)和側(cè)翻力矩系數(shù)呈現(xiàn)出先增大后減小的趨勢，側(cè)翻力矩系數(shù)相對其他兩項數(shù)值較小。隨著車速的增大，觀光巴士的側(cè)翻臨界風(fēng)速逐漸減小。

[關(guān)鍵詞]：斜風(fēng); 行車安全; 數(shù)值模擬; 靜力簡化

U461.1A

風(fēng)致行車安全一直是國內(nèi)外的研究熱點，近年來，車輛在斜風(fēng)作用下發(fā)生的交通事故頻頻報道[1]。我國高速公路發(fā)展迅速，為跨越江河湖海及山區(qū)峽谷，修建了一大批大跨度橋梁。而大跨度橋梁的海拔通常較高，易受到大風(fēng)的侵襲，車輛在橋上行駛過程中容易發(fā)生危險。因此，有必要對斜風(fēng)作用下橋上車輛的行駛安全進行研究，以保證旅客的人身安全。韓萬水等[2-3]建立了大跨度鋼桁梁風(fēng)-車-橋耦合系統(tǒng)。王少欽等[4]計算了鐵路懸索橋在列車及風(fēng)荷載作用下的振動響應(yīng)，并分析了響應(yīng)極值的產(chǎn)生機理及變化規(guī)律。韓艷等[5]提出了一種可以考慮抖振力空間相關(guān)性的風(fēng)-車-橋耦合振動分析方法，并將其制作成軟件程序。此外，還有很多學(xué)者都對風(fēng)-車-橋耦合振動進行了研究，并取得了一些研究成果[6-8]。但是這些研究通常要耗費大量的計算資源，無法對行車臨界風(fēng)速進行快速評價。本文以某橋上車輛為研究對象，采用CFD數(shù)值模擬計算車輛氣動力，并基于靜力簡化的方法，可以較快速地對車輛的行駛安全進行研究。

1 工程背景

某橋梁斷面為流線型箱梁形式，如圖1所示，其寬32.0 m，高3.0 m。一輛觀光巴士在橋上行駛，車輛高度為3.3 m，寬度為2.5 m，長度為10.4 m。為降低數(shù)值模型的建立難度，對觀光巴士的外形進行了一定程度的簡化，保留了車輛的主體外形，而忽略一些車輛的細(xì)部構(gòu)造，簡化后的車輛幾何模型如圖2所示。

2 車輛氣動力系數(shù)

車輛氣動力系數(shù)是計算行車臨界風(fēng)速的基礎(chǔ)，可以通過CFD數(shù)值模擬計算出橋上車輛的氣動力系數(shù)。在斜風(fēng)來流作用下，對車輛行駛安全影響最大的氣動力主要有側(cè)向力FS、升力FL和側(cè)翻力矩MR，車輛受力示意如圖3所示。

車輛的氣動力系數(shù)可定義為下式，其中CS、CL和CR分別代表車輛的側(cè)力系數(shù)、升力系數(shù)和側(cè)翻力矩系數(shù)，U0為來流風(fēng)速，Af為車輛正投影面積，L為車輛的長度，ρ為空氣密度，本文中取1.225 kg/m3。

CS=FS0.5ρU20Af

CL=FL0.5ρU20Af

CR=MR0.5ρU20AfL

（1）

采用ICEM軟件進行網(wǎng)格劃分，建立數(shù)值模型，整體計算區(qū)域如圖4所示，其中計算域尺寸為25B×15B，其中B為主梁寬度。主梁和車輛壁面設(shè)置多層貼壁層網(wǎng)格，首層網(wǎng)格高度為0.001 m，并對附近區(qū)域網(wǎng)格進行加密。靠近壁面的網(wǎng)格尺寸足夠小，可以保證了計算精度，遠(yuǎn)離壁面的網(wǎng)格尺寸逐漸增大，可以保證計算速度，網(wǎng)格總數(shù)控制在為280萬左右，細(xì)部網(wǎng)格如圖5所示。迎風(fēng)側(cè)邊界設(shè)為Velocity-inlet;背風(fēng)側(cè)邊界設(shè)為Pressure-outlet;上下邊界設(shè)置為Symmetry;前后邊界視來流風(fēng)偏角而定;主梁表面和車輛表面設(shè)為Wall。選用SST k-ω湍流模型;用SIMPLEC算法解決動量方程中速度分量和壓力的耦合問題;動量方程、湍動能方程及湍流耗散率方程均采用二階離散格式。

鐵路與公路王妍： 基于靜力簡化的斜風(fēng)作用下橋上車輛行駛安全研究

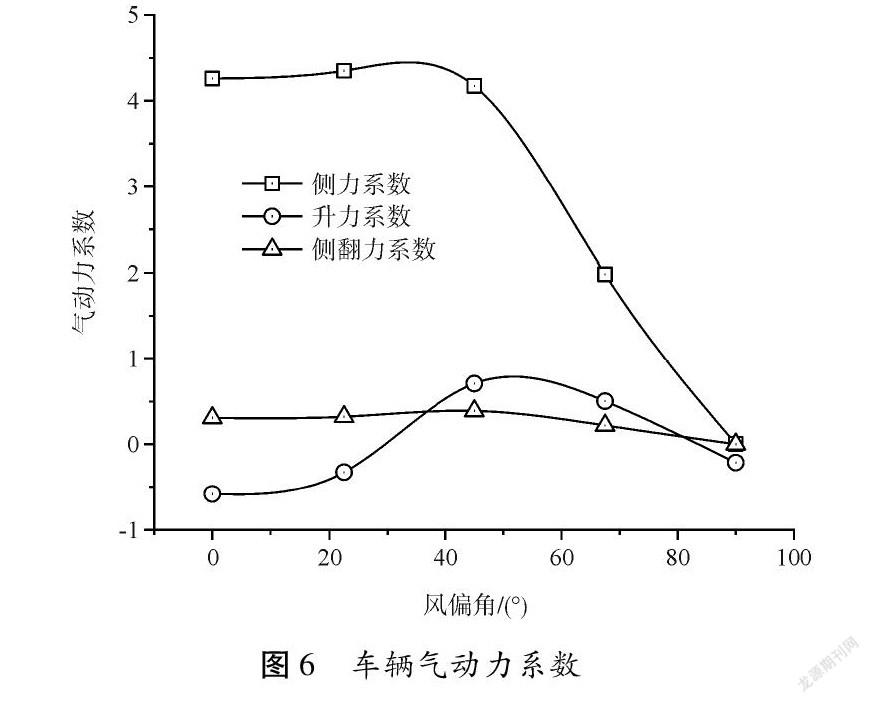
計算得到0～90°風(fēng)偏角來流下的車輛氣動力系數(shù)如圖6所示。由圖6可知，車輛的氣動力系數(shù)受風(fēng)偏角的影響明顯。隨著風(fēng)偏角增大，車輛的側(cè)力系數(shù)、升力系數(shù)和側(cè)翻力矩系數(shù)均呈現(xiàn)出先增大后減小的趨勢，側(cè)翻力矩系數(shù)相對其他兩項，數(shù)值較小。其中在0～45°范圍內(nèi)，側(cè)力系數(shù)的變化幅度很小。

3 行車臨界風(fēng)速

橋上車輛運動過程中同時受到風(fēng)荷載、重力和摩擦力的共同作用，車輛的受力示意如圖7所示。

風(fēng)致行車安全事故主要為側(cè)傾事故，主要與車輛受到的側(cè)力、升力、側(cè)翻力矩有關(guān)。值得注意的是，汽車在橋上行駛過程中，不僅受到自然風(fēng)引起的風(fēng)荷載，還有車輛運動引起的縱向風(fēng)荷載，二者的疊加才為車輛受到的實際風(fēng)荷載，記為Ure;相對風(fēng)向角記為θ，表達(dá)式如式（2）所示。車輛受到的合成風(fēng)荷載如式（3）所示。其中，U為自然風(fēng)的風(fēng)速，Uv為車輛行駛速度;CS（θ）、CL（θ）和CR（θ）分別為風(fēng)向角為θ時的車輛側(cè)力系數(shù)、升力系數(shù)和側(cè)翻力矩系數(shù)，可通過多項式擬合后進行取值。

Ure=U2+U2v

θ=arctan（Uv/U）（2）

FS=12ρU2reAfCSθ

FL=12ρU2reAfCLθ

MR=12ρU2reAfLCRθ

（3）

根據(jù)D’Alembert’s原理引入慣性力將車輛運動學(xué)問題簡化為靜力學(xué)問題處理，則車輛的橫向慣性力Fx與豎向慣性力Fy可表示為

Fx=-maxFy=-may（4）

式中：m代表車輛質(zhì)量，ax和ay分別代表車輛的橫向加速度和豎向加速度。

車輛受到的風(fēng)荷載的作用點與橋面有一定的距離，使得車輛頂部由迎風(fēng)側(cè)向背風(fēng)側(cè)傾斜，稱為總側(cè)翻力矩，它可分為氣動側(cè)翻力矩、氣動側(cè)向力和車輛橫向慣性力引起的力矩、氣動升力與車輛豎向慣性力產(chǎn)生的力矩，如式（5）所示。而重力則產(chǎn)生一定的力矩與之平衡，使車輛保持安全行駛狀態(tài)，稱為抗側(cè)翻力矩，如式（6）所示。當(dāng)二者相等時，則處在車輛側(cè)翻的臨界狀態(tài)，此時自然風(fēng)風(fēng)速大小則為側(cè)翻臨界風(fēng)速Ur。

MR+（FS+max）hvcosφ+（FL+may）·0.5Bcosφ（5）

mg·（0.5Bcosφ+hvsinφ）

（6）

當(dāng)風(fēng)偏角為0°時，車輛向前方行駛，其相對風(fēng)向角為正值，對圖6中3種氣動力系數(shù)進行多項式擬合，不同車速與風(fēng)速下的氣動力系數(shù)根據(jù)此公式進行取值。

經(jīng)過計算，當(dāng)不同車輛以不同速度行駛時，行車臨界風(fēng)速如圖8所示。由圖可知，隨著車速的增大，觀光巴士的側(cè)翻臨界風(fēng)速逐漸減小。當(dāng)車速為100 km/h時，車輛的臨界風(fēng)速為29.6 m/s。在極端大風(fēng)天氣下，可能發(fā)生危險。

4 結(jié)論

本文以斜風(fēng)來流下，在橋上行駛的觀光巴士為研究對象，研究了其行車安全性，得到結(jié)論：

（1）車輛的氣動力系數(shù)受風(fēng)偏角的影響明顯。隨著風(fēng)偏角增大，車輛的側(cè)力系數(shù)、升力系數(shù)和側(cè)翻力矩系數(shù)均呈現(xiàn)出先增大后減小的趨勢，側(cè)翻力矩系數(shù)相對其他兩項，數(shù)值較小。

（2）隨著車速的增大，觀光巴士的側(cè)翻臨界風(fēng)速逐漸減小。當(dāng)車速為100 km/h時，車輛的臨界風(fēng)速為29.6 m/s。在極端大風(fēng)天氣下，可能發(fā)生危險。

參考文獻

[1] Zhu L D， Li L， Xu Y L， et al. Wind tunnel investigations of aerodynamic coefficients of road vehicles on bridge deck[J]. Journal of Fluids and Structures. 2012， 30： 35-50.

[2] 韓萬水，趙越，劉煥舉，等.風(fēng)-車-橋耦合振動研究現(xiàn)狀及發(fā)展趨勢[J].中國公路學(xué)報，2018，31（7）：1-23.

[3] 韓萬水，劉煥舉，包大海，等.大跨鋼桁梁懸索橋風(fēng)-車-橋分析系統(tǒng)建立與可視化實現(xiàn)[J].土木工程學(xué)報，2018，51（3）：99-108.

[4] 王少欽，馬骎，任艷榮，等.主跨1120 m鐵路懸索橋風(fēng)-車-橋耦合振動響應(yīng)分析[J].鐵道科學(xué)與工程學(xué)報，2017，14（6）：1241-1248.

[5] 韓艷，陳浩，劉躍飛，等.橋梁抖振力空間相關(guān)性對風(fēng)-車-橋耦合動力響應(yīng)的影響[J].湖南大學(xué)學(xué)報（自然科學(xué)版），2015，42（9）：82-88.

[6] 舒鵬.變高度雙層鋼桁結(jié)合梁風(fēng)-車-橋耦合振動性能分析[J].四川建筑，2018，38（4）：134-136.

[7] 黃靜文. 基于風(fēng)-車-橋耦合振動的大跨度懸索橋車輛行駛安全性和舒適性研究[D].長沙：長沙理工大學(xué)，2018.

[8] 蘇波，齊冠，唐詩思，等.基于CFD的風(fēng)-車-橋系統(tǒng)耦合氣動力模擬研究[J].河南科學(xué)，2017，35（5）：778-786.