基于卡爾曼濾波算法的軌跡預測

邱 潤，黎敬濤，李孝疆，楊改娣，宋開雨

（昆明理工大學，云南 昆明 650504）

0 引言

自從20 世紀70 年代美國國家航空航天局（NASA）運用卡爾曼濾波解決阿波羅登月計劃的軌道預測問題后，卡爾曼濾波突破了當時工程領域維納濾波的局限，其原理是通過觀測值與理論實際數據融合得到當前的最佳預估值[1]。觀測數據中包含噪聲，卡爾曼濾波就是對包含噪聲的數據進行處理，卡爾曼最佳估計也可以看作是一個濾波過程[2]。卡爾曼濾波有兩種建模方法：一種是基于控制理論通過運動模型根據前一時刻的狀態來估計得到當前時刻的最佳估計值與協方差矩陣，以此類推進行下一時刻的最佳估計，這個建模求解的重點在于卡爾曼增益；另一種是利用一些概率性質進行建模的概率模型。本文將卡爾曼濾波運用到行車的軌跡預測中，通過運動系統方程、測量模型以及它們的誤差來求得卡爾曼增益，隨后用卡爾曼濾波后的值反過來修正誤差，從而在行車過程中獲得最佳的軌跡預測。

1 卡爾曼濾波理論

1.1 卡爾曼濾波的預測過程

（1）通過狀態估計公式得到此時刻的先驗估計值，即：

式中：和ut-1分別為上一時刻的先驗估計值和控制量，A為狀態轉移矩陣，B為控制矩陣。

（2）通過當前時刻的先驗誤差來表示系統包含的不確定性，即：

式中：Pt-1為上一時刻的誤差，Q為過程噪聲的方差。

在車輛的運行過程中，受傳感器測量精度問題的影響會存在方差為R的測量噪聲Vt。而建立的運動系統也不是百分百符合真實運動，即存在方差為Q的過程噪聲w。這兩個噪聲都服從期望為零的標準正態分布，即：

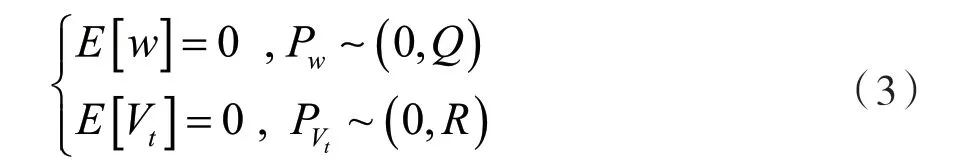
根據觀測矩陣H、先驗誤差以及測量噪聲的方差R，計算卡爾曼增益系數為：

（3）通過先驗估計值、真實值Zt與卡爾曼增益Kt，計算最佳估計值為：

隨著車輛運動的進行，系統會不斷積累誤差，需要通過協方差矩陣來不斷更新誤差[3]，即：

式中：Pt為更新后的誤差，I為單位矩陣。

1.2 卡爾曼濾波的最新研究

卡爾曼濾波擁有廣泛的應用領域，例如故障診斷[4]、系統監測[5-6]、巡航制導等[7]。文獻[8]在精密工程中運用擴展卡爾曼濾波進行故障診斷，對工程結構進行探傷，成功降低了測量噪聲的影響，準確鎖定損傷位置并掌握損傷程度。文獻[9]將卡爾曼濾波運用到建筑工程領域，通過建立時序預測模型對大壩的滲流、位移等檢測數據做出預測，從而掌握數據的變化趨勢，實現對大壩危險情況的預測。袁等人[10]運用低成本深度傳感器收集行人運動的數據，通過卡爾曼濾波獲取狀態的預估值，從而獲得行人的道路軌跡預測，彌補了傳統軌跡預測算法無法挖掘行走意圖的缺陷。

2 構建小車運動模型

2.1 簡化阿克曼運動模型

在全局坐標系XOY下，連接車輛重心（A，B兩點），將車輛的正前方視為橫軸指向（OB）、車輛的左側面視為縱軸指向（OA），建立參考坐標系xoy，如圖1 所示。嚴格來說，需要根據阿克曼轉向理論建立車輛的運動模型[11]。但是在合理的假設條件下，可以將車輛的運動看作是質點運動，將阿克曼轉向幾何模型簡化成自行車運動模型。將車輛前后四輪簡化為前后各一個輪，前后輪間用車軸進行連接[12]。

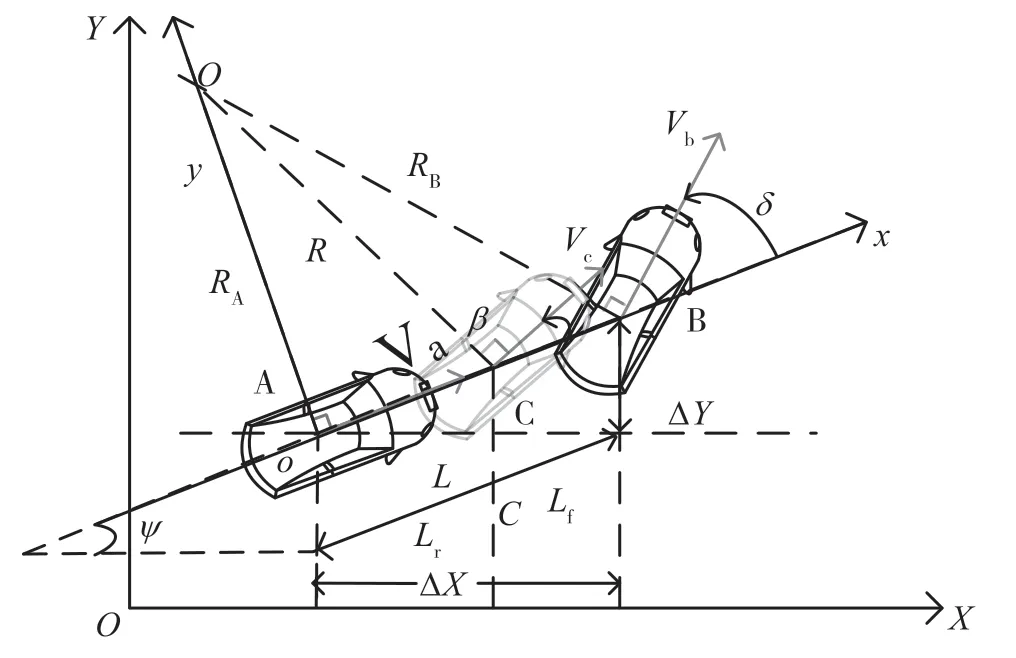
圖1 阿克曼轉向理論簡化模型

選取參考點C，ψ為車輛方向的橫擺角，δ為車輛轉向角度，β為車輛滑移角（車輛的航向與中心點速度Vc的夾角），L為小車的軸距。假設C 到前輪的距離為Lf，C 到后輪的距離為Lr，則Lf+Lr=L。對于自行車運動模型來說，小車每時每刻的速度方向都與過車身質點的旋轉半徑相垂直，即A 點的旋轉半徑RA（OA）垂直于Va，B 點的旋轉半徑RB（OB）垂直于Vb，C 點旋轉半徑R（OC）垂直于Vc。在相同的時間間隔內，小車在X方向和Y方向上位移的增量可以通過速度V來表示。

根據橫擺角計算起始兩點在全局坐標上的分速度，可以構建微分方程：

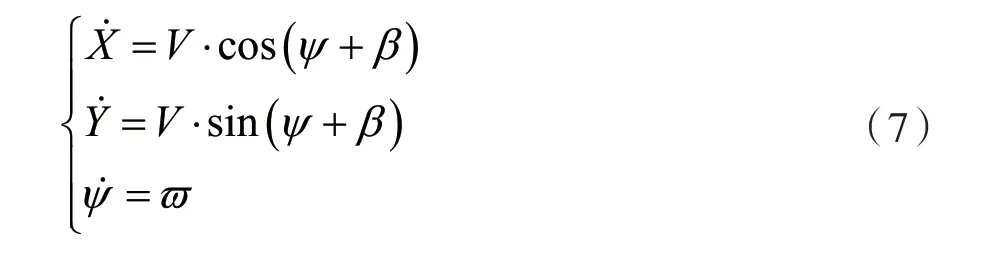
將點C 選在車輛后方，此時Lr=0，則Lf=L，這樣就可以達到任意時刻車輛的滑移角β為0。根據角速度公式可以得到：

通過車輛轉向角度δ可以計算出車輛的轉彎半徑R，根據速度進而可以得知橫擺角ψ。根據橫擺角度ψ，可以在單位時刻求出車輛在全局坐標系X方向的位移ΔX和在Y方向的位移ΔY，則小車的位移模型為：

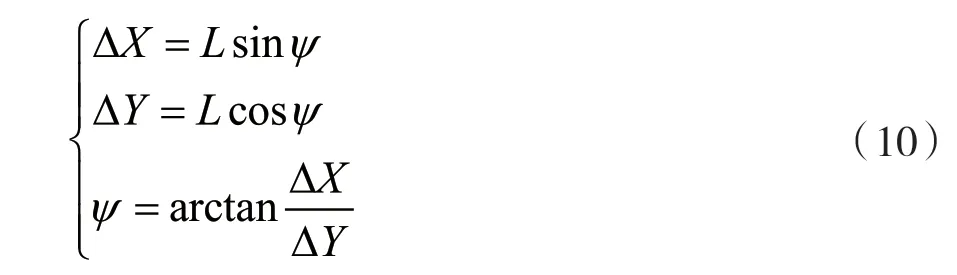
在全局坐標系中，當車輛平行于X軸運動時，初始t=0，擺角ψ0=0。當小車轉向δ0角度行駛到下一時刻（t=1）時，擺角更新為ψ1=ψ0+δ0=δ0；當t=2、轉向角為δ1時，擺角更新為ψ2=ψ1+δ1=δ0+δ1。由此可知，車輛擺角與轉向角的關系為ψt=ψt-1+δt-1。

2.2 卡爾曼濾波軌跡預測建模

將模型預測控制理論與狀態參數估計相結合，以此來預測車輛的運動軌跡[13]。根據小車在建模過程中的運動系統是否符合線性系統特征，可以將其運動具體區分為兩種狀態。一種是無轉向角時的直線運動，屬于線性運動系統；另一種是存在轉向角而不滿足線性要求的轉向運動，屬于非線性運動系統。在具體應用時，必須先將非線性系統線性化。

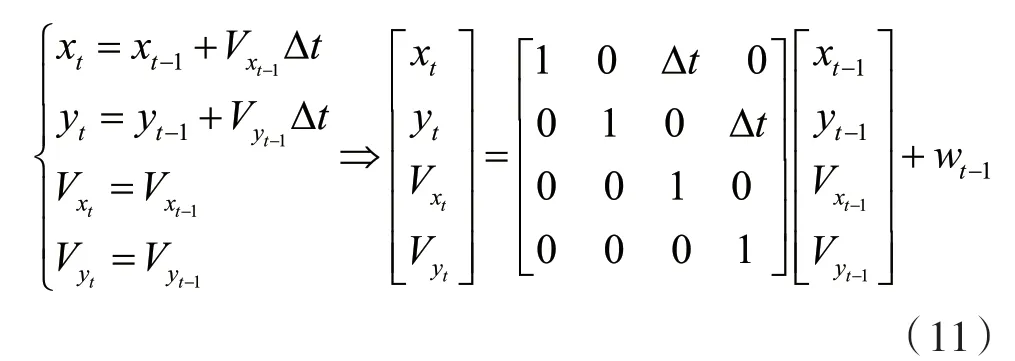
直線運動模型的輸出只取xt和yt的值，則根據觀測方程得到：

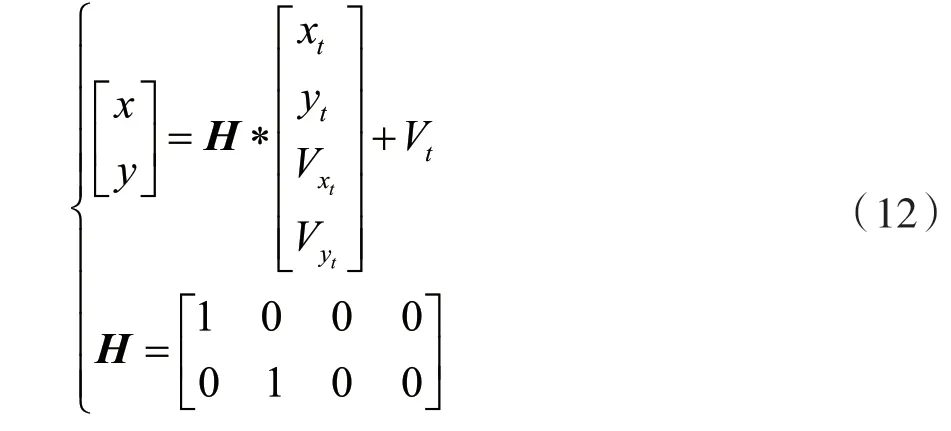
將小車的運動看作是簡單的自行車運動模型，當小車轉向時，車輛的轉向角度等于車輛前輪的偏角，如圖2 所示。

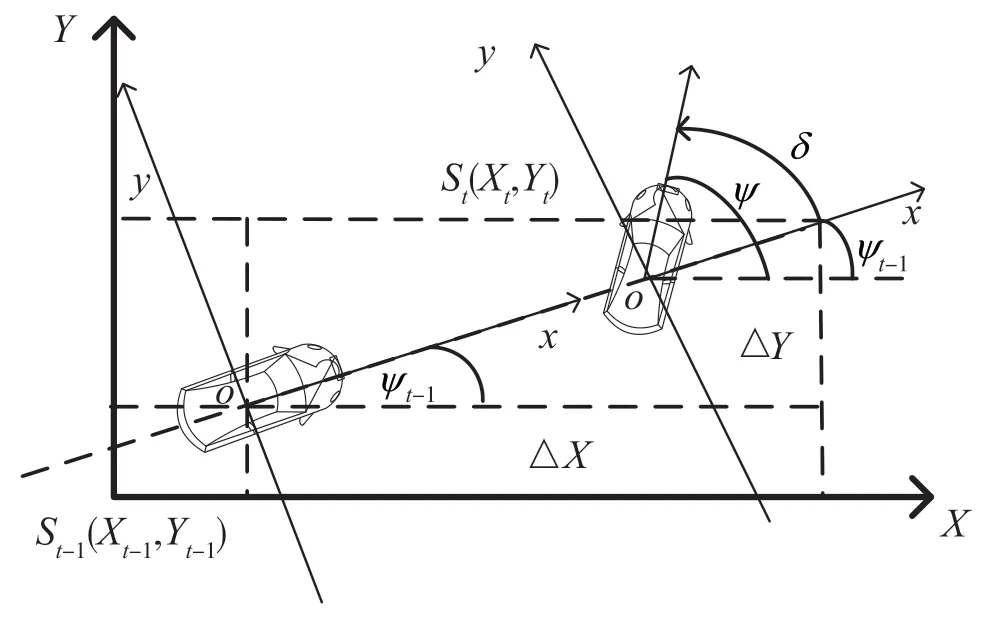
圖2 全局坐標系下的車輛運動

在全局坐標系中，小車通過單位時間由上一位置St-1行駛到當前位置St，空間狀態方程方程為：

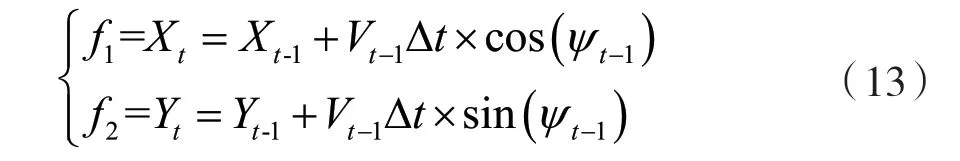
由于轉向運動系統的輸入方程包含三角函數，屬于非線性系統方程，因此需要通過泰勒級數將其線性化。通過狀態量X=[xy]T與控制量u=[vψ]T得到相應的雅克比矩陣A與B，即：

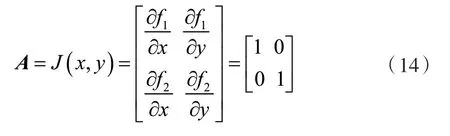
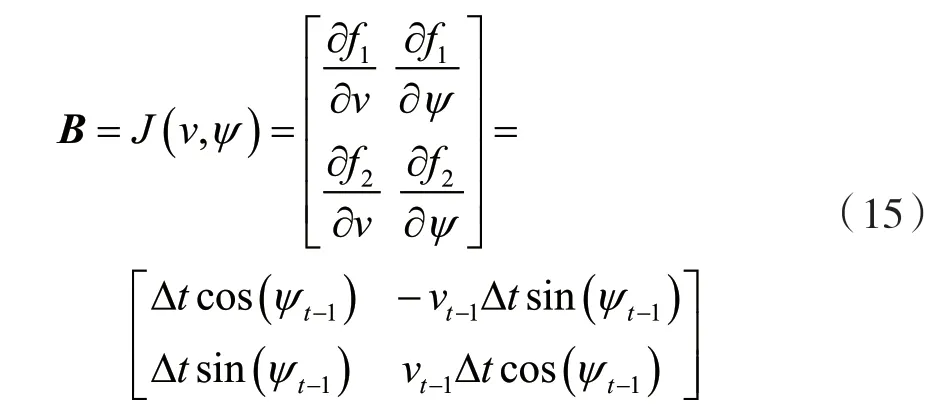
同直線運動一樣，這里輸出也只取xt和yt的值，根據觀測方程得到觀測矩陣H為單位矩陣。

3 卡爾曼濾波預測模型仿真分析

在Simulink 中進行實驗，建模主要分為車輛的物理建模部分和卡爾曼濾波部分。自行車縱向運動物理模型如圖3 所示，其中WhlAngF 為前輪轉向角，xdotin 為橫軸方向的速度，xdot 為車輛的橫向速度，ydot 為車輛的縱向速度，psi 為偏航角，r為偏航率，Fz-F 與Fz-R 為前后輪的法向力。此外，Info 端口包含該模型的所有信息，可以通過連接一個總線選擇器來選擇實驗所需的信息。

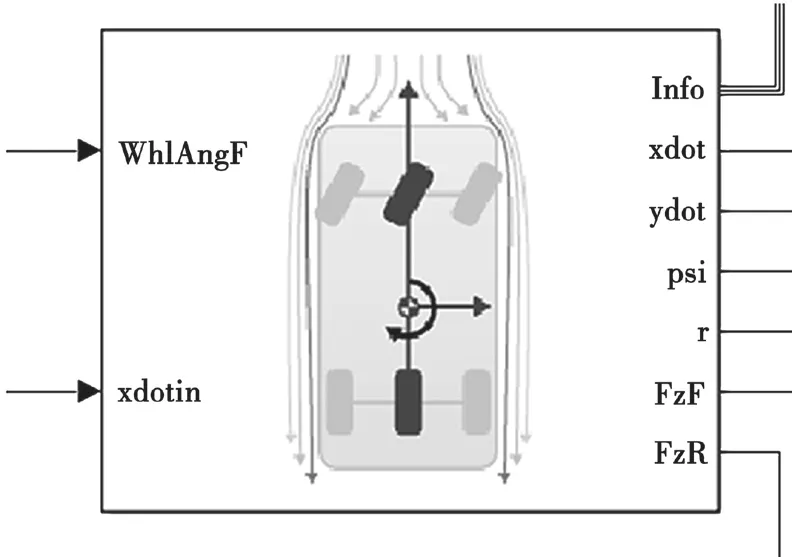
圖3 自行車運動模型

通過設置初始的橫向速度和車輛轉向角，得到車輛在某仿真時刻的橫向速度和縱向速度，進而可以得到某時刻的車輛狀態。設定橫軸方向速度為2 m/s、縱軸速度為0 m/s、仿真總時長為20 s、過程誤差為0.001 且測量誤差為0.1，則小車無轉向角的直線運動軌跡仿真如圖4（a）所示，小車轉向角45°下做轉向圓周運動的軌跡仿真如圖4（b）所示。

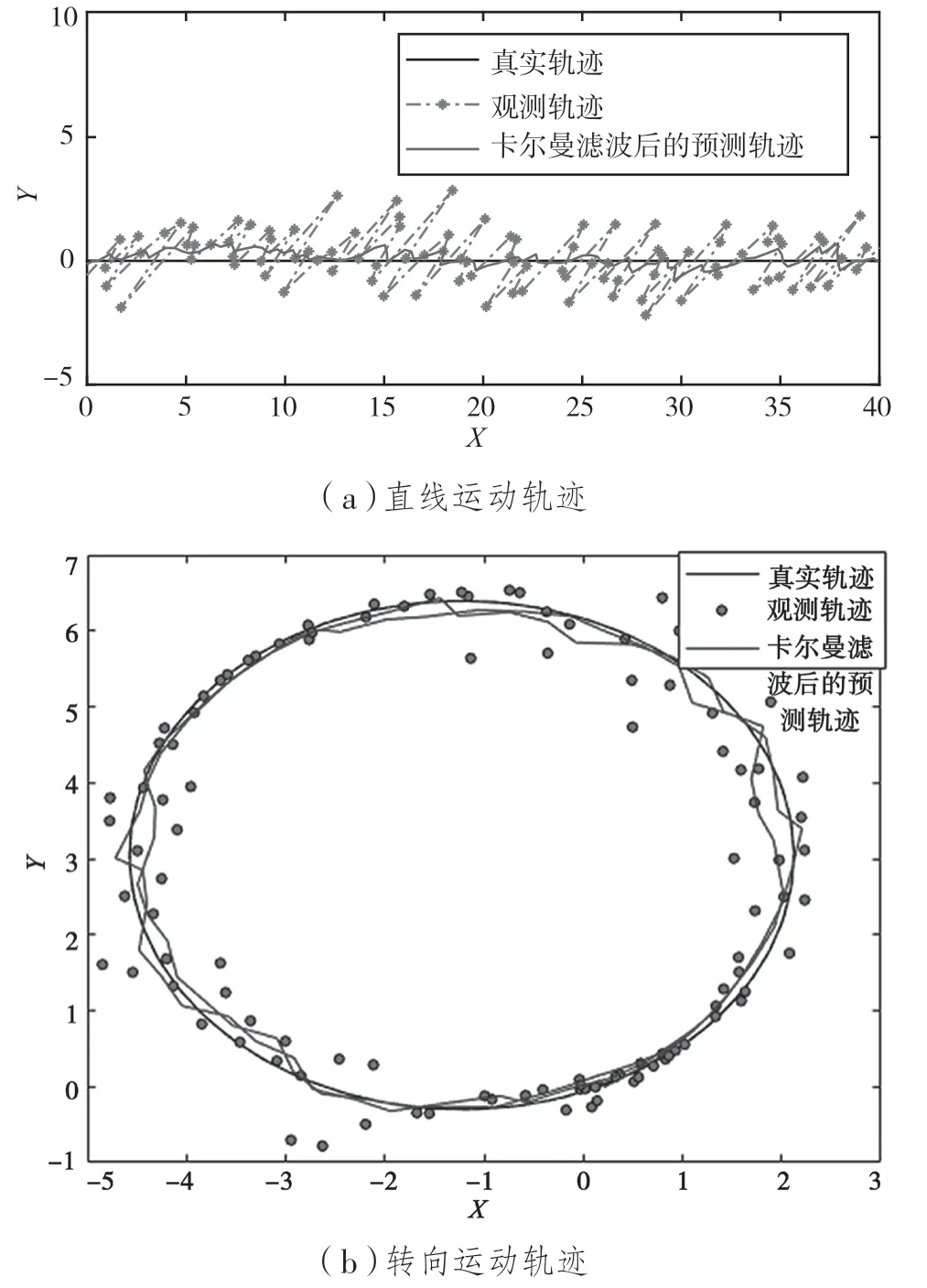
圖4 軌跡仿真結果

實驗表明，卡爾曼濾波后的預測軌跡相比于觀測軌跡更趨近于真實軌跡。

車輛在直線運動中真實軌跡值與測量軌跡值間的誤差如圖5（a）所示，真實軌跡值與卡爾曼濾波預測軌跡值間的誤差如圖5（b）所示。

根據圖5，在直線運動t=6.9 s 時，測量誤差約為2.2 m。經過卡爾曼濾波后，誤差約為1.2 m，與測量誤差相比減小了約1.0 m，證明卡爾曼濾波有效降低了誤差。

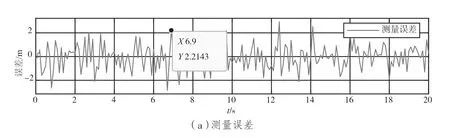
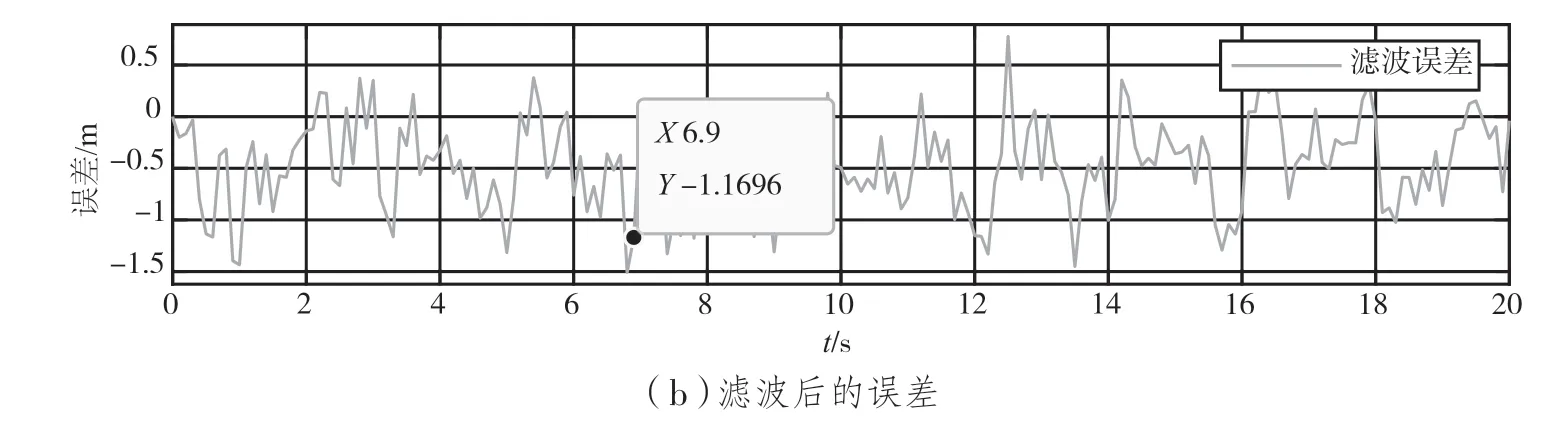
圖5 誤差對比

小車直線運動位移仿真結果如圖6（a）所示，轉向運動位移仿真結果如圖6（b）所示。

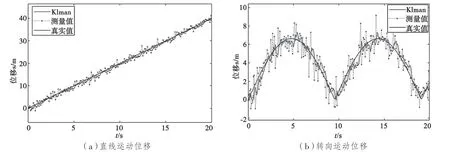
圖6 運動位移仿真

由圖6（a）可知，由于轉向角為0 且過程誤差較小，因此小車實際的位移呈線性增加，而且濾波后的估計值更趨近于真實值。由圖6（b）可知，由于測量值與真實值間的誤差較大，因此波動幅度也較大，通過卡爾曼濾波后的值相較于測量值更貼近于真實值。與此同時，由于小車從原點開始做圓周運動，因此從t=0 時刻開始，小車的位移先增加再減少，此后循環增加再減少。

4 結語

本文根據小車運動方程建立小車運動物理模型，通過Simulink 進行實驗仿真，驗證了卡爾曼濾波的軌跡預測的可行性。實驗表明，卡爾曼濾波后的軌跡比觀測出來的測量軌跡更加貼近于真實值，在測量誤差的基礎上降低了估計誤差。但是運用自行車運動模型對車輛建模進行了簡化，未來將基于詳細具體的阿克曼轉向原理進行建模分析。