輪軌磨耗對車輛系統動力學性能的影響

崔錦濤，楊湘平

（昆明鐵道職業技術學院 機車車輛學院，昆明 650208）

0 引言

近年來隨著我國鐵路行業的迅速發展，涉及鐵路運營過程中的安全性、經濟性問題日益突出[1-3]。尤其是輪軌磨耗問題受到廣泛的關注研究，該問題作為輪軌關系中的一個普遍問題。研究掌握輪軌磨耗的特征規律對于我國鐵路事業的發展和運營具有重大的理論和實際意義。車輪踏面磨耗是車輛運用過程中不可避免的一類現象，輪對的磨耗直接影響輪軌接觸關系、運行平穩性及安全性。目前，隨著輪軌磨耗程度的不斷加劇，車輛運行中的振動加速度也隨之增大，橫向穩定性及平穩性隨之下降[4]。輪軌磨耗對車輛的動力學性能有很大的影響。因此，研究車輛在不同磨耗下的動力學性能，對驗證輪軌接磨耗預測模型的準確性和保證列車運行安全可靠有重要意義。

1 動力學模型

車輛系統動力學模型屬于多剛體動力學理論，其系統組成部件及相互作用力繁多，由此產生的動力學行為更是存在較多的非線性因素。如何處理各部件之間的相互作用力和相對運動關系是建立動力學模型的基礎。車輛系統動力學建模主流方法是將垂向系統和橫向系統分別建模，根據輪軌接觸關系將橫向和垂向系統進行空間耦合處理，而輪軌接觸關系模型也存在多種輪軌接觸理論，針對本文所研究的內容，在建模過程中將起重要作用的因素表現出來[5]。本文將車輛系統視為多剛體系統，將懸掛系統視為等效線性剛度阻尼系統，其特性用數學模型來描述，通過錐形踏面和Hertz輪軌接觸理論將車輛的垂向運動和橫向運動耦合在一起。

1.1 車輛空間動力學模型

以CRH2型動車組為載體建立動力學模型。為了更接近實際情況，將車輛在橫向和垂向平面內的運動耦合起來，建立圖1所示的具有27自由度的車輛動力學分析模型。取車輛前進方向為X軸，水平向右為Y軸，與X軸和Y軸成右手坐標系的軸為Z軸。車體、轉向架及輪對的各個自由度的運動正方向按右手定則選取，該系統的自由度如表1所示。

表1 自由度參數列表

圖1 整車動力學模型

車輛系統空間動力學模型微分方程組可用矩陣形式表示為

1.2 Simulink模型

Simulink可以實現建模、仿真、動態分析的可視化仿真工具，以各種類型的子模塊可以搭建出線性系統、非線性系統及數字信號處理系統。本文使用連續系統模塊（Continuous）、數學運算模塊（Math Operations）、信號源模塊（Source）等建立車輛系統動力學模型。其基本思路是：利用過程信號連續時間積分模塊（Integrator）建立出車輛每個部件的動力學微分方程；以輸入輸出模塊定義方程中的每個變量，并建立該部件的微分方程組；將該微分方程組封裝為一個子函數，以多個車輛系統部件子函數形式建立整車系統模型，所建立的子函數如圖2所示。

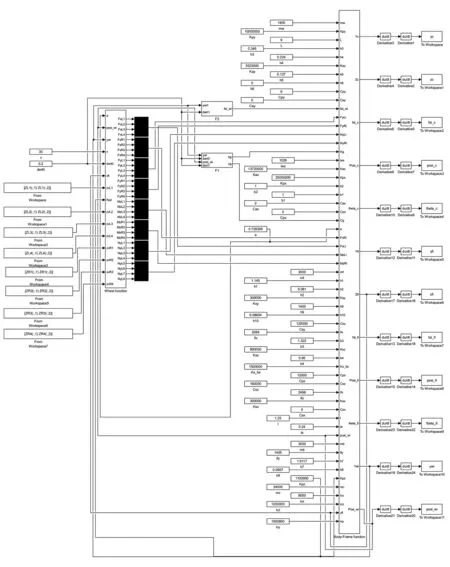
圖2 Simulink動力學模型

2 輪軌接觸模型

輪軌接觸模型[7]主要有3個部分:1）接觸幾何關系，即計算輪對相對于軌道給定位置的接觸點位置；2）輪軌接觸（蠕變和自旋）的動力學特性計算；3）根據幾何參數和運動參數計算接觸處的輪軌力和蠕滑力。

這些問題不是獨立解決的，一般需要通過迭代進行。本節所述的輪軌接觸相互作用幾何形狀的主要計算方法是根據輪軌截面曲線（剖面圖）的精確幾何形狀匹配進行的。為了提高接觸點位置計算的可靠性和速度，實現了兩個基本思想。首先，如果輪軌輪廓線沿著軌道運行方向是恒定不變的，在建模過程開始的時候，對輪軌輪廓線的接觸點坐標進行一次計算。根據車輪輪廓相對于鋼軌輪廓的位移，找出初始接觸點坐標。假設車輪相對于鋼軌有兩個自由度：繞縱軸旋轉（側滾）和橫向位移。在坐標計算過程中，輪軌接觸點下一次迭代計算（初始迭代點為車輪輪廓相對于鋼軌的當前位置）是通過上初始位置結算處的陣列矩陣進行插值計算得到的。這樣的做法可以減少算術運算數量，提高運算速度。本節介紹了我國幾種典型的車輪踏面類型，并分析了這幾種不同類型踏面類型靜態接觸幾何關系。

目前，我國高速鐵路動車組主要采用3種不同踏面。其中，CRH1型CRH2型動車組采用LMA踏面，CRH3型動車組采用S1002CN踏面，CRH5型動車組采用XP55踏面[6]。這幾種不同型號的踏面與60 kg/m靜態接觸幾何關系如圖3所示，其中：側滾角為0°；軌道傾角為1：40；橫向位移范圍為-15～15 mm；軌距為1435 mm。

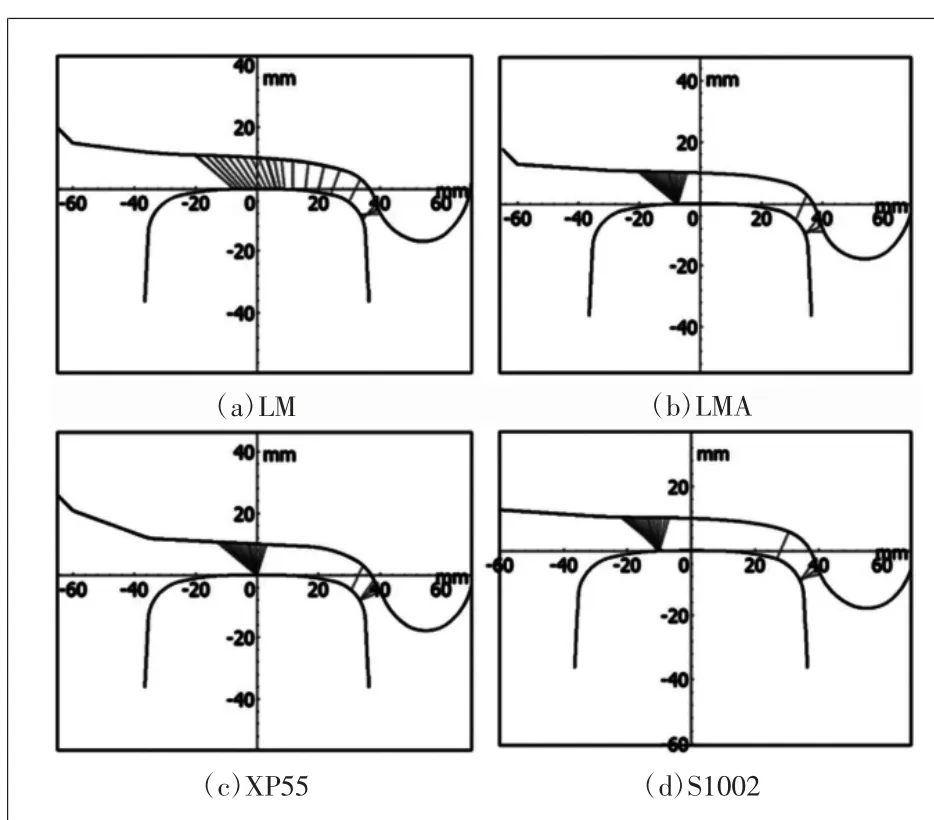
圖3 幾種踏面接觸靜態關系

根據輪軌磨耗預測模型仿真結果，結合現場運用數據，以動車組在一定運行里程后的磨耗踏面為研究對象，選取了輪軌磨耗預測結果中2種不同磨耗程度的踏面和標準60 kg/m匹配。其匹配關系如圖4所示，其中磨耗踏面2的運營里程大于磨耗踏面1。

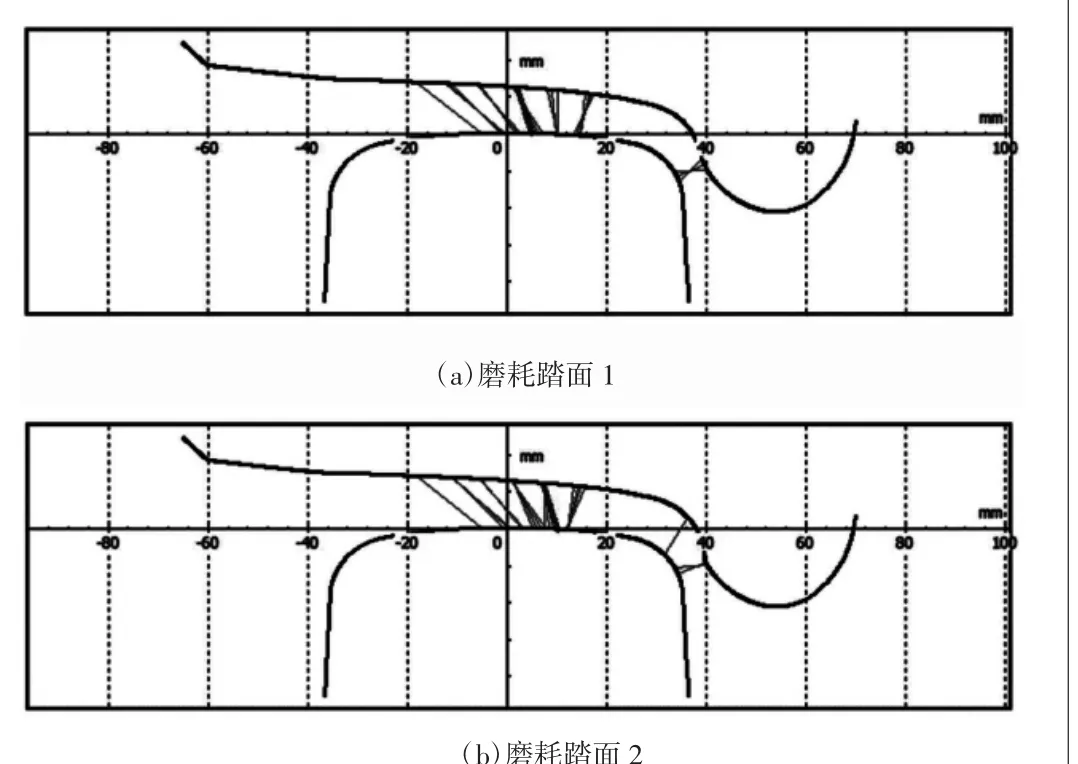
圖4 磨耗踏面接觸靜態關系

3 動力學性能分析

以GB 5599—1985《鐵道車輛動力學性能評定和試驗鑒定規范》為標準，對車輛在不同踏面狀態下的運行平穩性、臨界速度及非線性特性進行對比分析。

3.1 橫向穩定性分析

由于車輪踏面具有一定的錐度，當輪對沿著鋼軌滾動時，會產生一種既沿橫向運動又繞著軸質心的鉛錘軸向轉動的合成運動，當車輛運行速度達到一定值時，車輛的這種蛇行運動將會發生失穩。輪對一旦喪失穩定性，車輛各部件之間的作用力和振幅將明顯增大，車輛動力學性能也將急劇惡化，同時還會造成輪軌間的嚴重磨耗，且增加了發生車輪脫軌的危險性。隨著高速動車組運營速度的不斷提高，改善輪對橫向穩定性顯得尤為重要，而輪軌磨耗對于車輛的橫向穩定性影響也是需要考慮的一個重要因素。本節以兩種不同磨耗程度的踏面為研究對象，分析了車輛在匹配不同踏面時的蛇形臨界速度。

對標準輪軌和磨耗輪軌臨界速度計算結果如圖5所示。其中圖5（a）、圖5（b）分別為磨耗踏面1、2輪對橫向位移隨速度的不斷增大的時間歷程圖，從圖5（a）中可以看出隨著車速的不斷增大，輪對振動經由輪對平衡進入不穩定極限環最終進入穩定極限環的過程。其中磨耗踏面1不穩定極限環位于速度510 km/h附近。磨耗踏面2極限環位于475 km/h附近。從中可以看出車輪磨耗程度越大，其臨界速度降低。圖5（c）為匹配標準輪軌時，從中可以看出車輛的臨界速度為535 km/h。

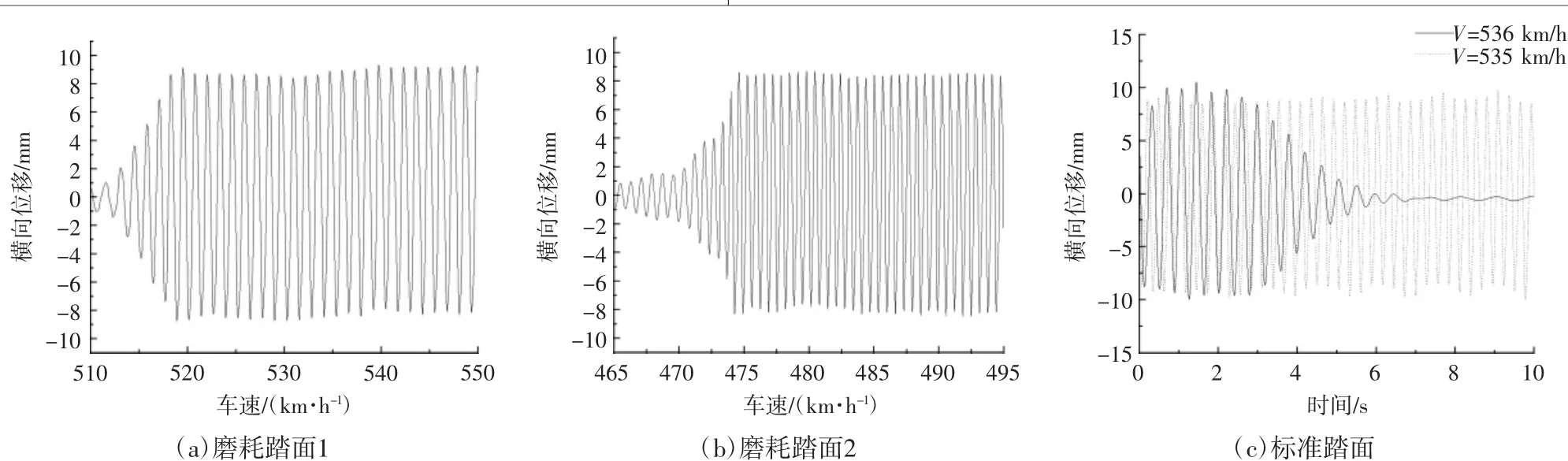
圖5 不同踏面臨界速度

3.2 非線性分析

考慮車輪和鋼軌之間的橫向間隙，當動車組高速運行時在軌道不平順等外界激擾的作用下，輪軌在橫向方向存在復雜的非線性行為。在分析輪對的蛇行運行時，由于存在輪軌間的黏著以及橫向間隙使得輪對橫向位移的響應會隨機地繞系統的極限環攝動，極限環的表現形式可以反映輪對的周期運動特性。研究表明，蛇行運動存在Hopf分岔行為[7-9]，為進一步探究輪軌磨耗對動車組的蛇行運動影響，以標準輪對和磨耗輪對為研究對象，計算分析了動車組輪對的橫向運動，如圖6所示。

對于一個非線性的系統而言，通常其極限環將以混沌方式出現，從而引起系統周期響應的本質變化，非線性車輛系統的蛇行運動一般會出現3種主要的分岔形式：亞臨界、吸引域超臨界和單點超臨界[10]。從圖6中可以看出，隨著踏面磨耗程度增加，其平衡位置趨于穩定。以此為依據可推斷，隨著磨耗的增加，蛇行運動分岔從吸引域超臨界進入單點超臨界，而本文中的系統是否經由亞臨界分岔發展而來，還需進行深入的研究分析。

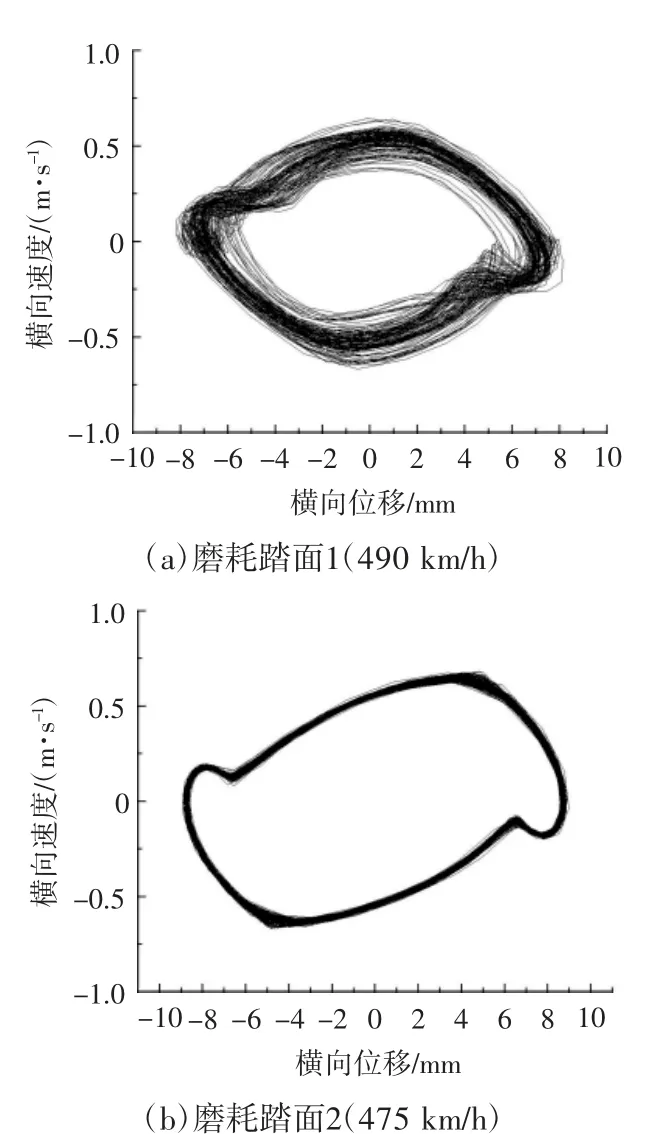
圖6 磨耗輪對橫向振動

3.3 運行平穩性

依據GB/T 5599-1985《鐵道車輛動力學性能判定和試驗鑒定規范》的規定，可以振動加速度作為車輛運行平穩性評價指標。以80、140、200、260、320、380 km/h的速度在直線線路上運行，對不同速度下的各項動力學指標進行計算分析。根據計算結果，在不同踏面狀態下運行的動車組的平穩性指標達到了一級等級。隨著踏面磨耗的加劇，橫向加速度指標逐漸增大，但對垂向加速度的影響并不大，車輛系統運行加速度如圖7所示，穩定性指標如圖8所示。

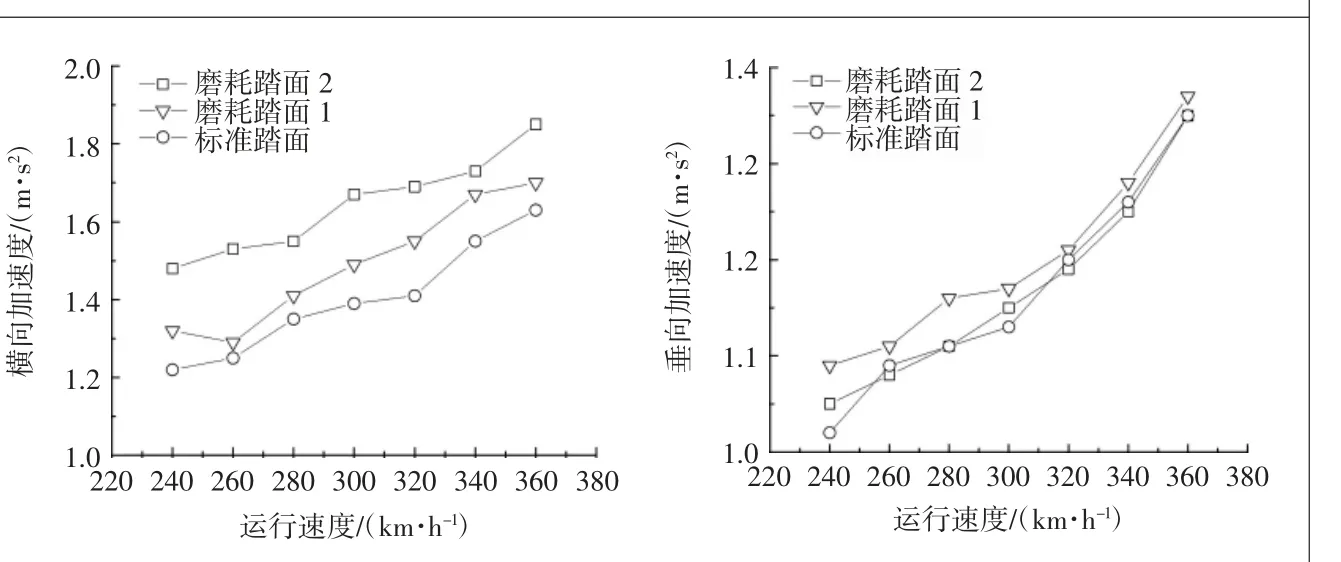
圖7 車輛最大加速度

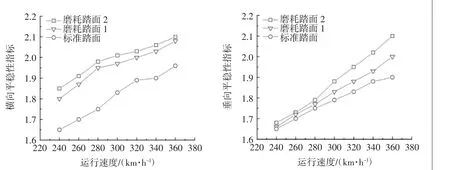
圖8 車輛平穩性指標

根據平穩性指標計算結果，在兩種磨耗程度不同的踏面狀態下，動車組的平穩性指標均滿足GB/T 5599-1985《鐵道車輛動力學性能判定和試驗鑒定規范》中一級等級要求。其動力學性能結果與加速度指標類似，踏面磨耗程度不斷增大導致了踏面等效錐度增加，從而導致車體橫向振動加劇；因其圓周磨耗較為均勻且未造成車輪圓度變化，因此對車體垂向振動影響不大。

4 結語

本文以CRH2型動車組為研究對象，以其動力學方程建立了Simulink仿真模型，結合輪軌磨耗預測結果分析了踏面磨耗對系統動力學性能的影響。考慮輪軌橫向間隙的存在,分析了輪對蛇行運動的非線性穩定性問題，將結論總結如下：

1）踏面磨耗會影響輪軌接觸點的分布情況，磨耗程度越大，其接觸點分布越不均勻。

2）隨著踏面磨耗程度增加，其輪軌參數也隨之變化，等效錐度增大導致了臨界速度降低，隨著磨耗程度的加劇，其臨界速度變小。

3）蛇行運動隨著磨耗的加劇而表現出較好的穩定性，Hopf分岔極限環振幅降低，雖然體現出極限狀態下的穩定性，其臨界速度的降低也起到了至關重要的作用。