隨機子空間模態參數識別精度的參數影響研究★
范倪圣,陳穩杰,周振綱
(嘉興學院建筑工程學院,浙江 嘉興 314001)
隨機子空間方法[1-2]只需要根據測點響應數據即可識別結構工作模態參數,但該方法進行模態識別時可能存在模態遺漏和出現虛假模態問題[3-5],對于此,國內外學者通過采用穩定圖方法或模糊聚類方法等對其進行了改進,在一定程度上避免了出現虛假模態問題,較好地解決了隨機子空間方法系統階數n取值問題。然而,該方法的識別精度實際還會受到方法中相關參數(如Hankel矩陣行數i、測點數L,識別用到的測點響應數據量s)取值的影響。國內個別學者就Hankel矩陣行數i對隨機子空間方法模態參數識別精度問題做了初步研究[6-7]。但同時考慮參數i和s不同取值組合對隨機子空間方法模態參數識別精度的影響規律研究還尚未見相關報道。因此,為了將隨機子空間方法更好地應用于環境激勵下實際工程結構的模態參數識別中,有必要對參數s和i不同取值組合對隨機子空間方法模態參數識別精度的影響規律問題進行研究。
1 隨機子空間方法模態參數識別方法
采用基于協方差的隨機子空間方法進行結構模態參數識別時,首先根據各測點的加速度響應測試數據構造如式(1)所示的Hankel矩陣。
(1)
其中,H為Hankel矩陣;Hp為Hankel矩陣過去分塊矩陣;Hf為Hankel矩陣未來分塊矩陣;yk(k=0,…,2i+j-2)為根據測點響應數據構造的列向量,上述構造的列向量的行數為測點數L;i和j分別為Hankel矩陣分塊矩陣的行數和列數,Hankel矩陣的分塊矩陣的行數和列數應滿足關系式s=2i+j-1,s為計算時選取的測點響應數據數量。
根據生成的Hankel矩陣過去分塊矩陣和未來分塊矩陣按式(2)計算得到Toeplitz矩陣T:
(2)
對T矩陣按式(3)進行奇異值分解:
(3)
其中,U,S,V均為T矩陣經奇異值分解得到的矩陣,U和V為正交矩陣,S為對角矩陣;S1為S矩陣的分塊矩陣,其為對角矩陣,對角元素T為矩陣異值分解得到的正奇異值,S1∈Rn×n;U1和U2為U矩陣的分塊矩陣,U1∈RLi×n,U2∈RLi×(Li-n);V1和V2為V矩陣的分塊矩陣,V1∈RLi×n,V2∈RLi×(Li-n)。
系統的觀測矩陣Γ及其逆矩陣Γ-1可表示為:
(4)
(5)
其中,Γ∈RLi×n;Γ-1∈Rn×Li。
根據式(6),式(7)計算得到矩陣P1和P2。
P1=Γ-1(1∶n,1∶L(i-1))
(6)
P2=Γ(L+1∶Li,1∶n)
(7)
其中,P1∈Rn×(Li-L+1);P2∈R(Li-L)×n;Γ-1(1∶n,1∶L(i-1))為取Γ-1矩陣第1行至第n行和第1列至第L(i-1)列范圍內元素的構成的矩陣;Γ(L+1∶Li,1∶n)為取Γ矩陣第L+1行至第Li行和第1列至第n列范圍內元素的構成的矩陣。
系統的狀態矩陣A和輸出矩陣Q可表示為:
A=P1P2
(8)
Q=Γ(1∶L,1∶n)
(9)
其中,A∈Rn×n;Q∈RL×n;Γ(1∶L,1∶n)為取Γ矩陣第1行至第L行和第1列至第n列范圍內元素的構成的矩陣。
對計算得到的狀態矩陣A按式(10)進行特征值分解:
A=EDE-1
(10)
其中,E為特征向量構成的矩陣,E∈Rn×n;D為特征值構成的對角矩陣,D∈Rn×n。矩陣E和矩陣D的元素都為復數。
提取矩陣D的對角線元素構成列向量Z,即:
Z={z1z2…zn}T
(11)
其中,zk為Z向量的第k行元素值,其大小等于D矩陣第k行的對角元素值;Z∈Rn×1。
根據式(12)計算得到識別模態頻率列向量Ft。
Ft=abs(ln(Z)·fs)/2π
(12)
其中,fs為測點響應測量的采樣頻率,Hz;π為圓周率;ln(·)函數為對復向量元素進行自然對數運算;abs(·)函數為對復向量元素進行取模運算;Ft∈Rn×1。
根據輸出矩陣Q和狀態矩陣A特征值分解得到的特征向量構成的矩陣E按式(13)計算復矩陣G。
G=QE
(13)
按式(14)計算得到識別模態振型向量構成的振型矩陣Mt。
Mt=abs(G)*sign(180·(|angle(G)|-π/2)/π)
(14)
其中,angle(·)函數為對復矩陣元素進行取相位運算;abs(·)函數為對復矩陣元素進行取模運算;sign(·)函數為符號函數,當因變量分別為正值、零和負值時,函數值分別取1,0和-1。
2 隨機子空間方法模態參數識別精度評價方法
本文主要就參數i和s取值對基于協方差的隨機子空間方法的模態頻率和模態振型的識別精度影響規律進行研究。以下對本文模態頻率和模態振型識別精度計算方法進行簡介。
2.1 模態頻率識別精度評價方法
前述隨機子空間方法識別得到的結構的各階模態頻率構成的列向量Ft可表示為:
(15)
其中,ftk為根據試驗測量數據由隨機子空間方法識別得到的第k階模態的模態頻率,k=1,2,…,m,m為識別模態數。
與隨機子空間方法識別得到的各階模態對應的結構真實的模態頻率構成的列向量Fa可表示為:
(16)
其中,Fa∈Rn×1;fak為與隨機子空間方法識別得到的第k階模態對應的結構真實的模態頻率,k=1,2,…,m,m為識別模態數。
根據式(17)可計算得到隨機子空間方法識別得到的各階模態的模態頻率識別精度。
(17)
其中,eFk為與隨機子空間方法識別得到的第k階模態的模態頻率識別精度。
參數i和s取值對隨機子空間方法不同階模態的模態頻率識別精度的影響有一定差異,故本文采用按式(18)計算得到的模態頻率平均識別精度指標EM來對隨機子空間方法模態頻率識別精度進行評價。EM值越大則隨機子空間法的模態頻率整體識別精度越高。
(18)
其中,m為識別模態數。
2.2 模態振型識別精度評價方法
前述隨機子空間方法識別得到的結構的各階模態振型構成的振型矩陣Mt可表示為:
(19)
其中,φtk為根據試驗測量數據由隨機子空間方法識別得到的第k階模態的模態振型列向量,k=1,2,…,m。
與隨機子空間方法識別得到的各階模態對應的結構真實的模態振型向量構成的振型矩陣Ma可表示為:
(20)
其中,φak為與隨機子空間方法識別得到的第k階模態對應的結構真實的模態振型列向量,k=1,2,…,m。
模態振型識別的精度可采用識別模態振型與真實模態振型的模態保證準則MAC值來評價。反映隨機子空間方法各階模態的模態振型識別精度的MAC值可按式(21)計算得到。
(21)
其中,MACk為隨機子空間方法識別得到的第k階模態模態振型的MAC值。
參數i和s取值對隨機子空間方法不同階模態的模態振型識別精度的影響有一定差異,故本文采用按式(22)計算得到的模態振型平均模態模態保證準則MACM值對隨機子空間方法模態振型的識別精度進行評價。MACM值越大則隨機子空間法的模態振型整體識別精度越高。
(22)
3 五質點的彈簧-質量-阻尼系統模態識別算例
五質點的彈簧-質量-阻尼系統算例模型如圖1所示。算例模型的質量、剛度和阻尼參數如表1所示。
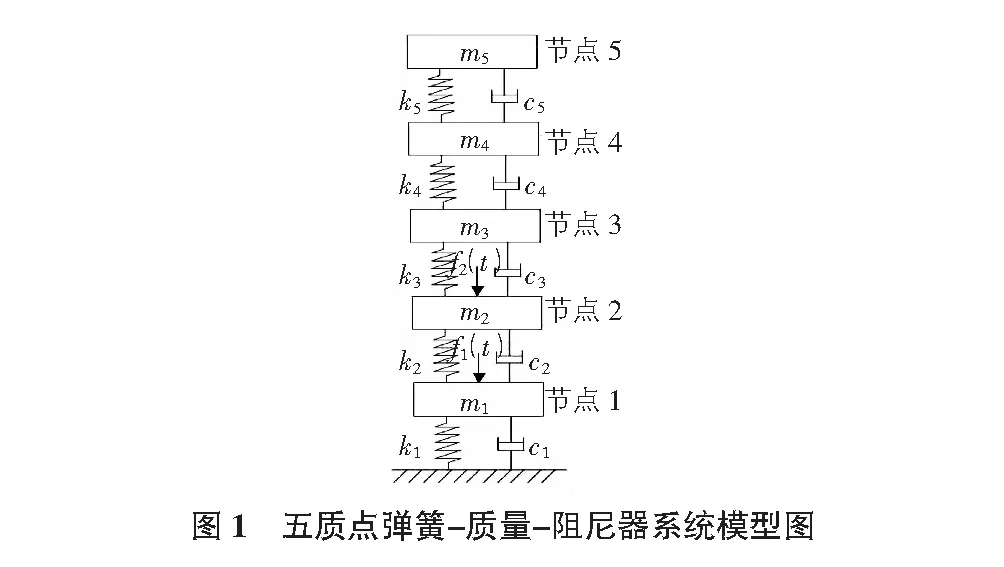
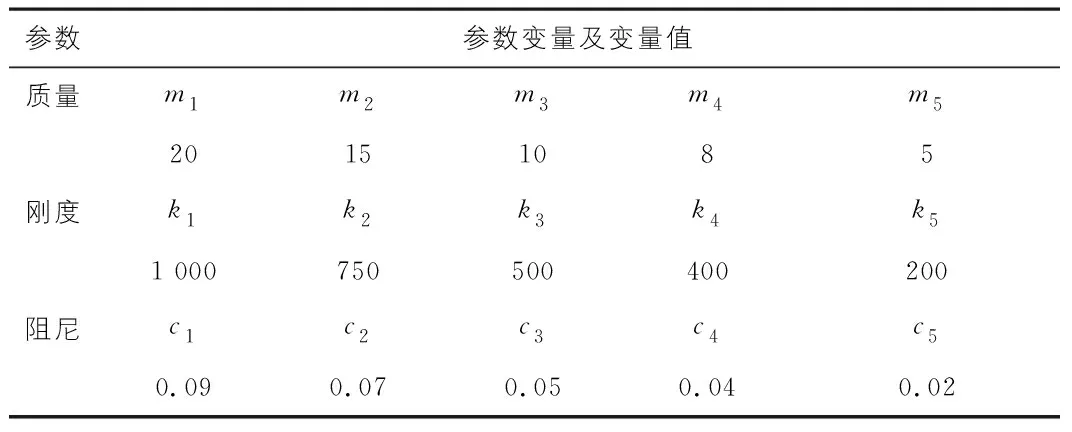
表1 算例模型參數
在該算例模型的節點1和節點2處施加豎向白噪聲激振力f1(t)和f2(t)來模擬算例模型系統受到的環境激勵,通過計算獲得各節點豎向加速度響應數據作為本文隨機子空間方法模態識別的測點響應數據。
根據各節點的動力平衡關系可建立算例模型受上述白噪聲激勵時的動力方程[8],如式(23)所示。
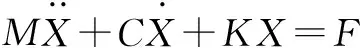
(23)
(24)
(25)
(26)
(27)
(28)
(29)
(30)
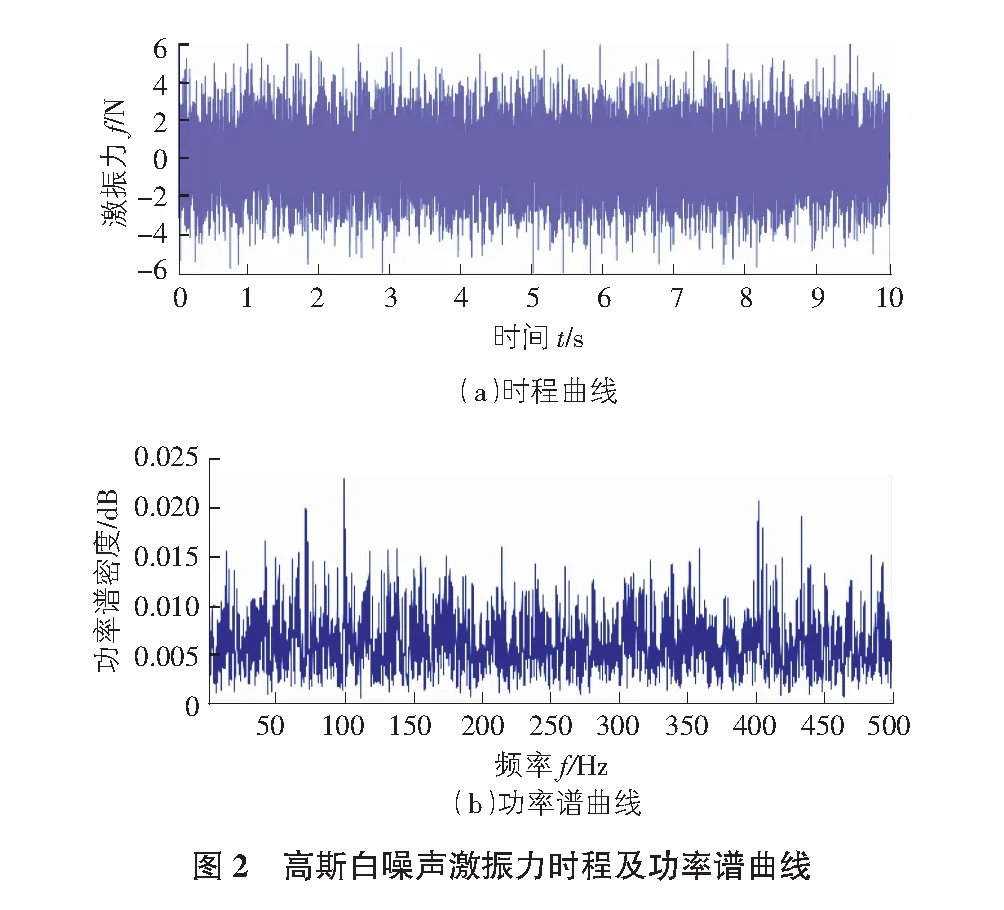
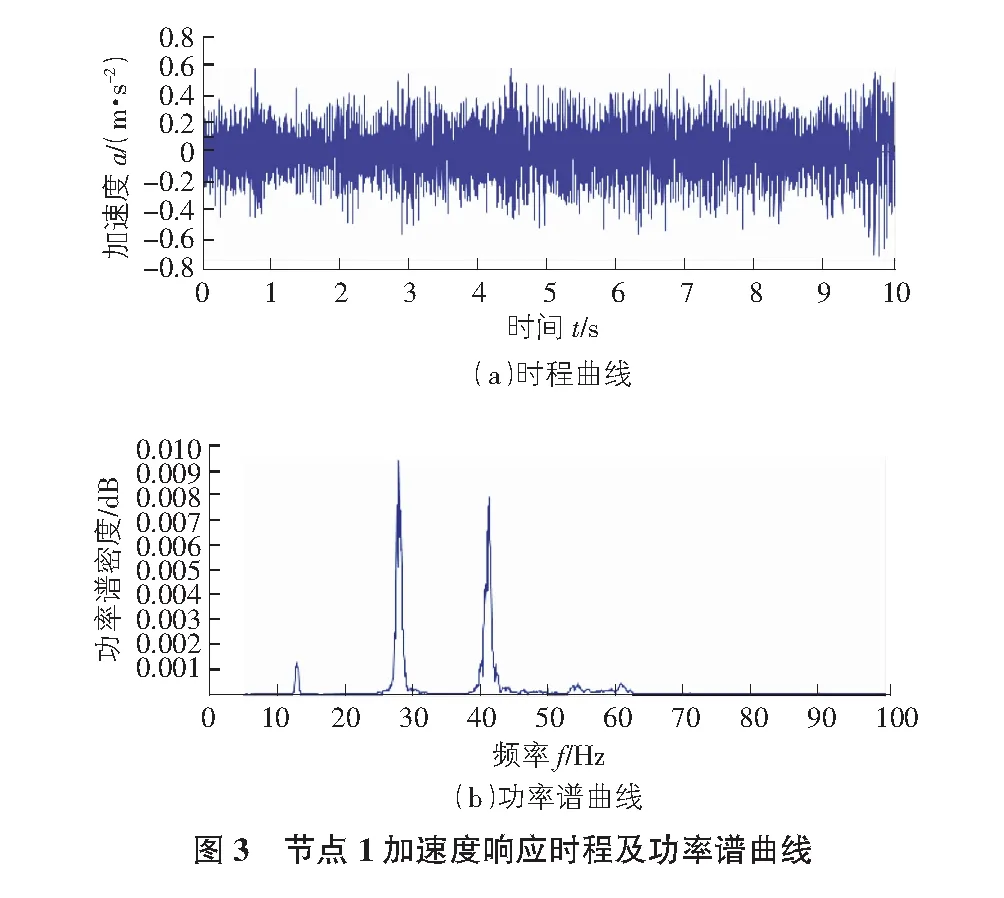
在節點1和節點2處均輸入相同的高斯白噪聲激勵力,高斯白噪聲激振力時程及功率譜曲線如圖2所示,激振力時長為10 s,步長為0.001 s。采用Newmark-β法用Matlab軟件編程求解算例模型動力響應時程。限于篇幅,此處僅給出節點1加速度響應時程及功率譜曲線,如圖3所示。
算例模型的模態頻率和歸一化模態振型的真實值(理論值)可通過對式(23)忽略阻尼項和無激振力時得到的無阻尼自由振動方程進行特征值和特征向量分析計算得到。算例模型的模態頻率和模態振型真實值分別如表2,圖4~圖8所示。
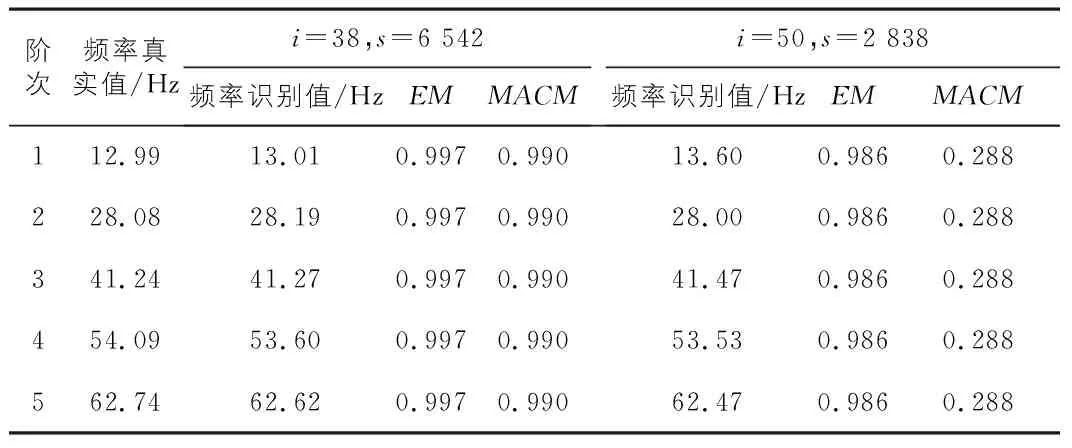
表2 i和s不同取值時隨機子空間法模態頻率和模態振型識別平均精度初步比較


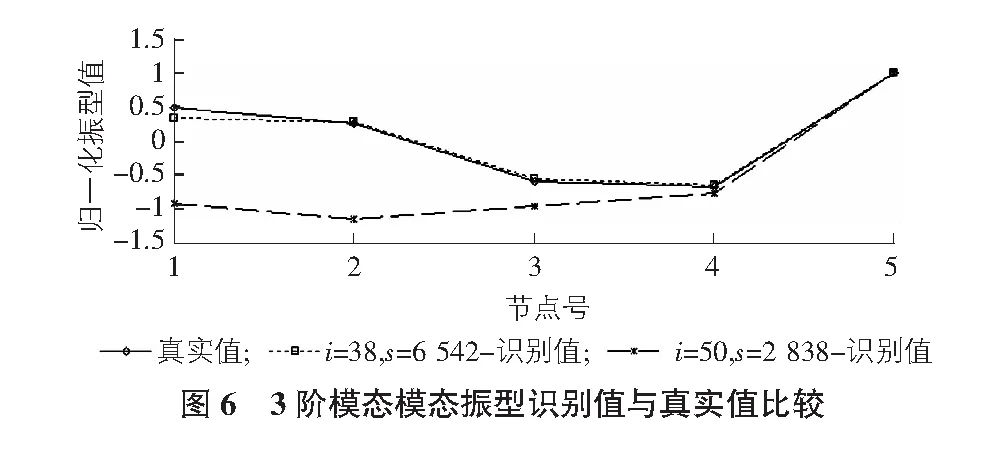
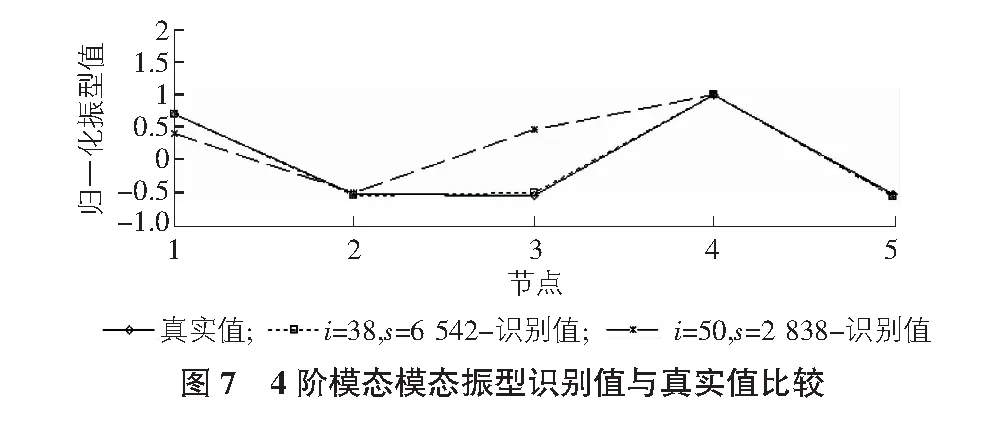
在測點數L=5和系統階次n=12取值一定時,對i=38,s=6 542和i=50,s=2 838兩種參數取值情況根據前述基于協方差的隨機子空間模態參數識別方法對算例模型進行了模態參數識別計算,識別得到的各階模態頻率和模態振型如表2,圖4~圖8所示。同時,給出了兩種參數取值情況時模態頻率平均識別精度指標EM值和模態振型平均識別精度指標MACM值,如表2所示。
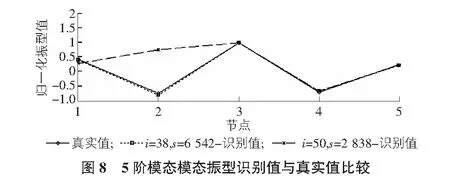
由表2,圖4~圖8可知:i=38,s=6 542時隨機子空間方法識別得到的算例模型各階模態頻率和模態振型識別值與其真實值非常接近,EM和MACM都接近于1;而i=50,s=2 838時模態頻率和模態振型的平均識別精度要低于i=38,s=6 542取值情況。由此可見,參數i和s取值對隨機子空間方法模態參數識別精度有一定影響,故有必要對參數i和s取值對隨機子空間方法模態參數識別精度的影響規律進行研究。
4 i和s取值對模態參數識別精度影響規律研究
為了進一步研究參數i和s取值對隨機子空間方法模態參數識別精度的影響規律,對i和s不同取值組合時采用隨機子空間方法對前述算例模型的模態頻率和模態振型進行了識別計算,并計算得到了各取值組合時模態頻率平均識別精度指標EM值和模態振型平均識別精度指標MACM值。參數i和s不同取值組合構造時參數i取值從30到158,增量為2,參數s取值從2 000到8 998,增量為2,共構造了227 500個i和s不同取值組合。識別計算中測點數L=5和系統階次n=12保持不變。
圖9給出了i和s不同取值組合時采用隨機子空間法識別得到的算例模型的模態頻率平均識別精度指標EM值變化情況。
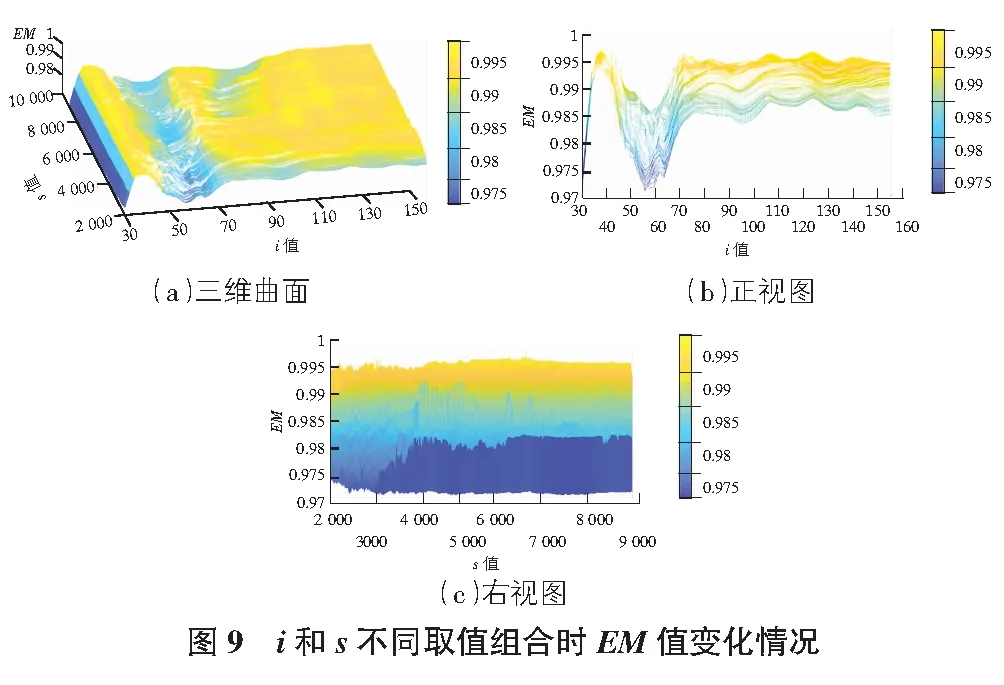
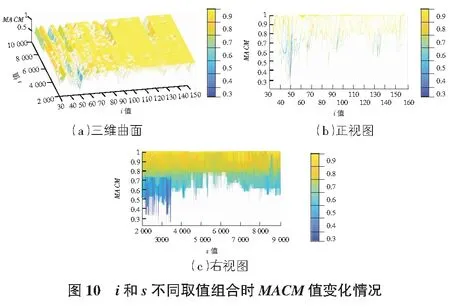
圖10給出了i和s不同取值組合時采用隨機子空間法識別得到的算例模型的模態振型平均識別精度指標MACM值變化情況。
由圖9可知:參數i和s不同取值組合時,隨機子空間法模態頻率的平均識別精度指標EM值均較大,EM值在0.971~0.998范圍內變化,表明隨機子空間法識別算例模型的模態頻率具有很高的精度。參數i和s不同取值對隨機子空間法模態頻率的平均識別精度指標EM有一定影響,主要表現為:
1)當參數i在42~110取值范圍內時,參數s取值對模態頻率平均識別精度指標EM的影響相對較明顯。
2)參數i取值對模態頻率平均識別精度指標值EM的影響相對明顯,參數i取值在36~42及110~158取值范圍內時,模態頻率平均識別精度更高。
由圖10可知:參數i和s不同取值組合時,隨機子空間法模態振型的平均識別精度指標MACM值變化較大,MACM值在0.283~0.999范圍內變化,表明參數i和s取值對隨機子空間法識別算例模型的模態振型的精度影響較大。參數i和s不同取值對隨機子空間法模態振型的平均識別精度指標MACM的影響主要表現為:
1)當參數i在30~96和130~136取值范圍內時,參數s取值對模態振型平均識別精度指標MACM的影響較明顯。
2)參數i取值對模態振型平均識別精度指標MACM的影響明顯,參數i取值在22~24,32~36,60~62,72~78,82~84,102~120,136~138,142~148及156~158取值范圍內時,模態振型平均識別精度較高,MACM值基本在0.7及以上。
綜上可知:
1)參數i和s取值對隨機子空間法模態頻率的平均識別精度指標EM有一定影響,但影響總體相對較小。
2)參數i和s取值對隨機子空間法模態振型的平均識別精度指標MACM影響較大。
3)參數i和s在若干取值范圍內取值組合時隨機子空間法的模型頻率及振型均具有較高的識別精度,如i取36~38,s取2 500~7 000時,模態頻率的平均識別精度可達0.99以上,模態振型的平均識別精度可達0.8以上。
5 結論及展望
本文以一五質點的彈簧-質量-阻尼系統的模態參數識別算例為例,對參數i和s取值對基于協方差的隨機子空間方法的模態頻率及模態振型的識別精度影響進行了研究。主要結論如下:
1)參數i和s不同取值組合時隨機子空間法模態頻率的平均識別精度指標EM值在0.971~0.998范圍內變化,變化幅度較小,表明參數i和s取值對隨機子空間法模態頻率的平均識別精度影響相對較小,但仍有一定影響,同時也表明隨機子空間法識別模態頻率具有很高的精度。
2)參數i和s不同取值組合時隨機子空間法模態振型的平均識別精度指標MACM在0.283~0.999范圍內變化,變化幅度較大,表明參數i和s取值對隨機子空間法模態振型的平均識別精度影響較大。
3)參數i和s在若干取值范圍內取值組合時隨機子空間法的模型頻率及振型均具有較高的識別精度。
本文對參數i和s不同取值組合時隨機子空間法模態頻率和模型振型的平均識別精度的影響進行了初步研究。為了更好地將隨機子空間方法應用于環境激勵下實際工程結構的模態參數識別中,后續將結合相關數學方法對參數i和s合理取值方法進行進一步的研究。

