基于斷裂力學的材料低溫疲勞壽命估算模型改進研究

潘韋廷， 薛齊文， 王尕平， 杜秀云

(1.大連交通大學土木工程學院，遼寧 大連 116028；2.武漢生態環境設計研究院有限公司，湖北 武漢 430050;3.大連理工大學工業裝備結構分析重點實驗室，遼寧 大連 116023；4.遼寧師范大學物理與電子技術學院，遼寧 大連 116029)

目前，基于斷裂力學的方法是低溫環境下結構疲勞壽命評估和壽命預測研究最主要手段之一[1]，該方法關鍵問題在于疲勞裂紋擴展速率模型的建立。現如今Paris公式作為研究疲勞裂紋擴展速率方面最基本的模型被廣泛使用，盡管Paris公式對低溫環境下大多數材料裂紋擴展的中速率區擬合結果較好[2]，但未能考慮環境溫度對材料性能的影響且需大量試驗數據進行擬合。嘗試如何有效建立新的低溫疲勞裂紋擴展速率模型，有助于將低溫疲勞裂紋擴展微觀機理與宏觀力學模型聯系起來，進而更好的滿足工程實際的需求[1]。眾多學者對低溫疲勞裂紋擴展速率模型的建立進行了探索，Yokobori等[3]提出的改進模型將熱激活理論及位錯動力學引入Paris公式，并對Paris公式進行溫度修正；Tanaka等[4]將不同溫度環境下相同材料疲勞裂紋擴展速率存在相同低溫臨界擴展點的觀點代入Paris公式中，提出改進的疲勞裂紋擴展速率模型。這些模型雖都能對低溫環境下材料裂紋擴展速率曲線進行擬合，但預測精度仍不能保證甚至某些結論與事實存在出入的情況。如何直觀且合理的描述環境溫度對裂紋擴展速率的影響，進而構建低溫下疲勞壽命估算模型仍需進一步的討論和研究。

最近，一些學者認為Zheng和Hirt提出的改進擴展模型不僅能夠較好的對低溫環境下疲勞裂紋擴展速率曲線進行擬合，還能簡單預測金屬材料低溫疲勞裂紋擴展速率曲線[5-7]。Zheng和Hirt[8]從裂紋擴展機理與金屬拉伸性能的角度出發，在靜態斷裂模型的基礎上引入Schwalbe[9]提出的裂紋擴展應力強度因子門檻值Kth的概念，并結合疲勞裂紋擴展系數建立疲勞裂紋擴展速率模型，但并未對該模型關鍵參數Kth做進一步的分析與研究。文獻[10]通過考慮疲勞極限及材料形核裂紋臨界長度對應力強度因子門檻值Kth的影響，得到了Kth的函數模型。在此基礎上，文獻[5]進一步通過材料疲勞極限在低溫與室溫(20 ℃)時的變化關系并結合室溫環境下材料應力強度因子門檻值，得到了關于材料應力強度因子門檻值Kth在低溫下的預測模型。但低溫環境下材料疲勞極限的變化較為復雜，與環境溫度、材料的抗拉強度、屈服強度等因素密切相關，且影響關系尚未明確，因此低溫疲勞極限的確定仍需進一步探討與研究。

本文在考慮低溫環境下裂紋擴展門檻值的基礎上，利用材料抗拉強度、屈服強度以及環境溫度構建函數，對低溫環境下材料疲勞極限進行估算，建立改進的低溫環境下斷裂力學疲勞壽命估算模型。

1 基于斷裂力學的疲勞壽命估算模型

現階段大部分低溫疲勞裂紋擴展速率模型都是在Paris公式基礎上加以改進得到。由于Paris公式參數較多且不易獲取的特點，文獻[8]基于改進靜態斷裂模型提出了一種考慮裂紋擴展應力強度因子門檻值ΔKth的疲勞裂紋擴展速率模型：

(1)

式中：B為疲勞裂紋擴展系數，可通過材料的彈性模量E計算得到；ΔK為應力強度因子幅值，可由裂紋尺寸相關的形狀修正系數Y、試驗荷載最大應力σmax以及裂紋長度a表示；ΔKth為裂紋擴展應力強度因子門檻值，計算式參考文獻[10]。

(2)

(3)

(4)

式中：lc為形核裂紋臨界長度，取決于材料微觀組織，不隨溫度變化而變化；σR為材料的疲勞極限。

故低溫環境下裂紋擴展應力強度因子門檻值ΔKth的遞推模型可進一步表示為[5]：

(5)

式中：ΔKth(T0)和ΔKth(T)分別為室溫及低溫下的裂紋擴展應力強度因子門檻值；σR(T0)和σR(T)分別為室溫及低溫下的材料疲勞極限。

將式(2)和式(5)代入式(1)中可得低溫環境下疲勞裂紋擴展速率的估算模型：

(6)

在常幅荷載作用下，文獻[11]認為對疲勞裂紋擴展速率模型進行積分來估算材料的疲勞壽命是合理的，疲勞壽命估算模型可表示為：

(7)

式中：a0和ac分別為初始裂紋尺寸和臨界裂紋尺寸；Nf為從初始裂紋擴展到臨界裂紋的應力循環數。

文獻[12]根據材料試件的疲勞極限σR和疲勞裂紋擴展應力強度因子門檻值ΔKth并結合Haddad MHE短裂紋理論得到了初始裂紋尺寸：

(8)

臨界裂紋尺寸ac可由材料斷裂韌性計算得到：

(9)

式(9)中：KIC為材料的斷裂韌性，可由BS7910推薦的以沖擊韌性為參量的模型以及溫度和板厚為參量的模型兩者所得結果取較小值的方式確定[1]。

將式(6)代入式(7)中可得改進的低溫疲勞壽命估算模型：

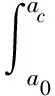
(10)

相較于Paris公式和文獻[8]提出的模型，式(10)建立的低溫疲勞壽命估算改進模型考慮了材料疲勞極限在低溫環境下的變化對疲勞壽命所帶來的影響，使疲勞壽命估算結果具有更高的可信度和實用性，但對于低溫環境下疲勞極限的確定及環境溫度對疲勞壽命的影響還需進一步討論和研究。

2 基于低溫環境材料特性變化的疲勞壽命改進模型

相較于常溫環境而言，低溫環境下疲勞裂紋擴展速率因環境溫度的改變而變得復雜。本節基于低溫環境材料特性變化的角度對上述疲勞壽命估算模型進行改進。由式(10)的改進模型可以看出低溫下疲勞裂紋擴展速率與材料力學性能密切相關，彈性模量、疲勞極限等因素直接或間接影響疲勞裂紋擴展速率。部分研究表明溫度變化會改變材料力學性能從而進一步影響材料疲勞極限，文獻[13]和[14]給出了通過引入溫度敏感因子對低溫下結構鋼屈服強度、抗拉強度以及彈性模量隨溫度變化規律進行分析得到的擬合模型：

(11)

σb=σ′bexp[qb(T0-T)]

(12)

E(T)=E(T0)+b(T-T0)

(13)

式中：σy，σb分別為低溫下材料的屈服強度和抗拉強度；σ′y，σ′b分別為室溫下材料的屈服強度和抗拉強度；E(T0)為室溫下材料的彈性模量；qs，qb，b分別為溫度敏感系數；T0，T分別為所對應的常溫和環境溫度。

現階段大多數研究采用Goodman公式以及Soloberg公式對材料疲勞極限進行估算。由于在工程實際中往往試驗條件有限，不宜考慮過多的試驗參數，本文僅考慮低溫環境下材料屈服強度及抗拉強度的變化對疲勞極限的影響，對參數σR進行修正，可通過兩種方法實現。

方法1：材料疲勞極限具有熱激活性質，可將低溫環境下材料疲勞極限σR定義為非熱激活分量和熱激活分量的疊加，建立疲勞極限熱激活模型。

σR(T)=σR(T0)+ΔσR

(14)

式中：σR(T)為低溫下材料疲勞極限；σR(T0)為常溫下材料疲勞極限(非熱激活分量)，可近似表示為與材料室溫下抗拉強度σ′b有關的擬合函數[15,16,17];ΔσR為熱激活分量，與屈服強度σy的熱激活分量近似相等[15]。故低溫疲勞極限表達式可進一步寫成：

(15)

式中：k與材料性質等有關，可擬合得到。

將式(11)代入式(15)中，則改進的低溫疲勞極限估算模型為：

(16)

將式(13)、式(16)代入式(10)中得到按照方法1改進的低溫疲勞壽命預測模型1：

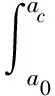
da

(17)

方法2：低溫環境下疲勞極限主要受材料力學性能(屈服強度、抗拉強度)影響，可引入溫度敏感因子q對疲勞極限與環境溫度的關系進行擬合，估算模型為：

σR(T)=σR(T0)exp[q(T0-T)]

(18)

將式(13)、式(18)代入式(10)中得到按照方法2改進的疲勞壽命預測模型2：

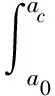
(19)

采用上述模型對低溫材料疲勞極限σR進行改進后，可以較為直觀的反映出當環境溫度降低時，材料疲勞極限和裂紋擴展應力強度因子門檻值增大，所對應的疲勞壽命增加；當環境溫度升高時，材料疲勞極限和裂紋擴展應力強度因子門檻值減小，所對應的疲勞壽命減少，這與試驗數據的趨勢保持一致。此外，疲勞極限改進模型相較于Goodman公式以及Soloberg公式而言所需參數更少，且主要參數獲取較為簡單，適合在工程實際中進行應用。

3 算例數值驗證

為驗證所提模型的估算能力，依據文獻[1]、[18]給出的橋梁結構鋼Q345qD母材及其對接焊縫試驗數據進行低溫環境下的疲勞極限和疲勞壽命估算，通過所建模型的估算值與試驗值進行對比，驗證所提模型估算的準確性及適用性，并與其它模型估算結果進行對比。

3.1 Q345qD鋼材母材的壽命

3.1.1 屈服強度、抗拉強度以及彈性模量估算

Q345qD鋼板是專用于架設鐵路和公路橋梁的常用材料，其母材在不同溫度條件下屈服強度、抗拉強度以及彈性模量試驗值如表1所示，將表中試驗數據代入式(11)、式(12)和式(13)中，可得到母材屈服強度、抗拉強度及彈性模量隨環境溫度變化的估算模型。

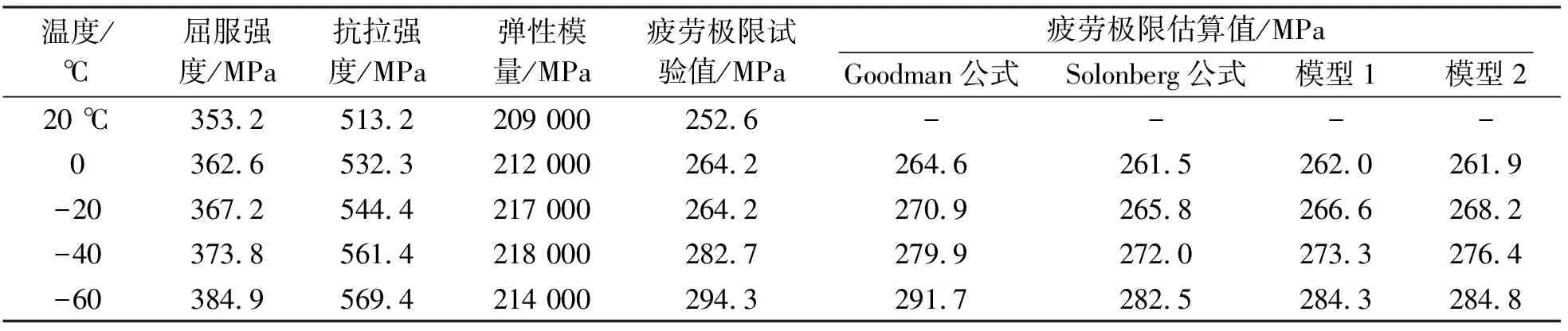
表1 不同溫度下Q345qD鋼材母材力學指標及疲勞極限值

屈服強度：σy=353.2exp[0.001 08(20-T)]

(20)

抗拉強度：σb=513.2exp[0.001 52(20-T)]

(21)

彈性模量：E(T)=209 000-110(T-20)

(22)

3.1.2 疲勞極限估算

不同溫度環境下母材疲勞極限試驗值以及不同模型的估算結果如表1所示。

3.1.3 裂紋擴展應力強度因子門檻值估算

由文獻[1]可知，20 ℃室溫條件下應力比R為0.1時試件厚度為14.0 mm的Q345qD鋼材母材門檻值為3.106 MPa·m1/2，通過改進模型可得母材裂紋擴展應力強度因子門檻值估算值如表2所示。

由表2可知，利用改進模型所得估算結果在低溫環境下(0～-60 ℃)略低于試驗值，但該種方法大大減少了計算裂紋擴展門檻值所需的參量，預測結果總體在可接受范圍之內，對于工程結構來說偏安全，該方法具有一定的可行性。

3.1.4 疲勞壽命估算

根據低溫環境下Q345qD母材有效初始裂、臨界裂紋、疲勞極限等關鍵參量，運用本文提出的改進模型對材料疲勞壽命進行估算，結果如表3、表4所示。

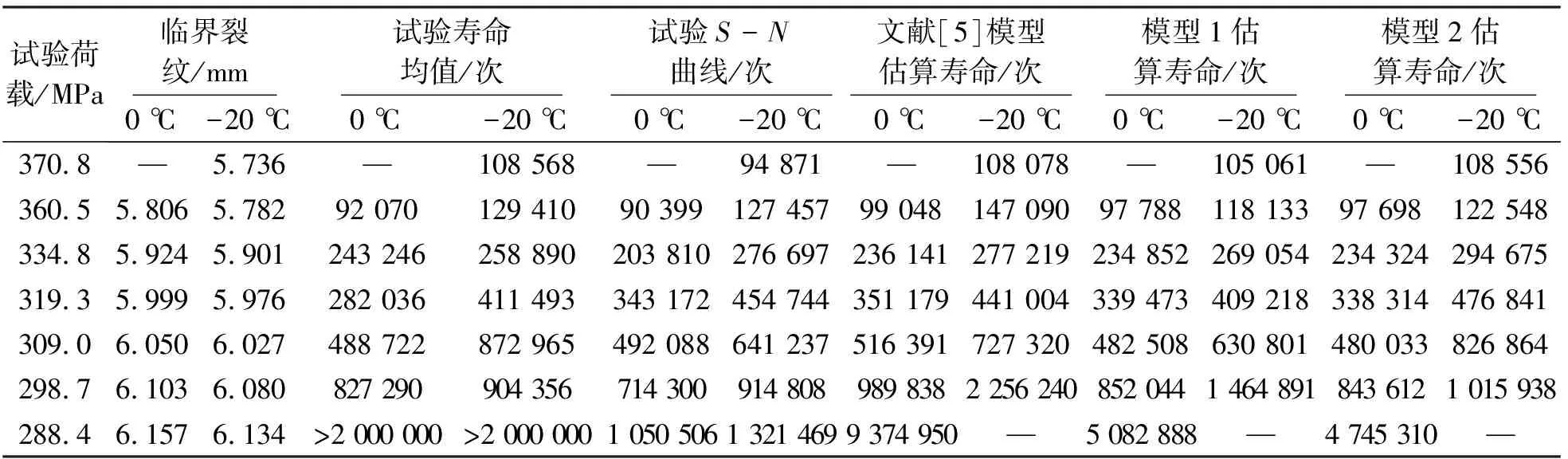
表3 0 ℃和-20 ℃Q345qD鋼材母材疲勞壽命估算值

由表4可知：對于Q345qD母材，在0、-20、-40、-60 ℃四種不同低溫環境下，本文提出的改進模型均能夠對該材料的疲勞壽命進行有效的估算；相較于其他模型，改進模型估算結果更接近于試驗值。

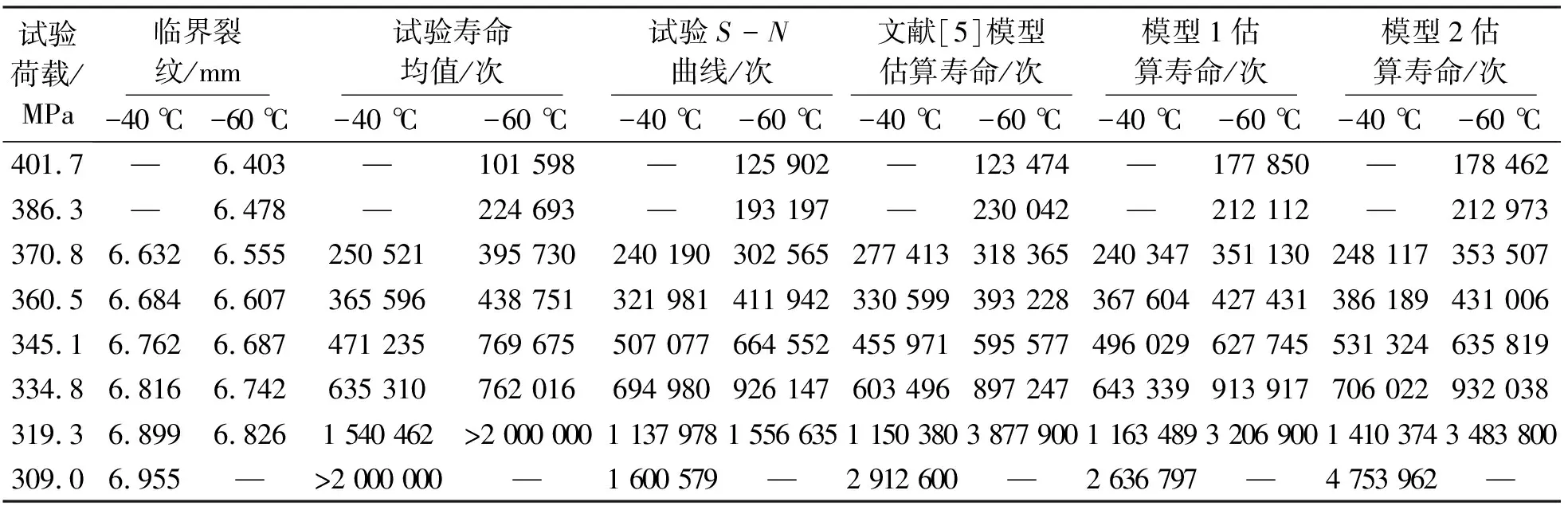
表4 -40 ℃和-60 ℃Q345qD鋼材母材疲勞壽命估算值

3.2 Q345qD鋼材對接焊縫的壽命估算

3.2.1 屈服強度、抗拉強度以及彈性模量估算

對接焊縫作為鐵路及公路橋梁中板件和型鋼常用的拼接方式，其疲勞斷裂問題在工程實際中不容忽視。Q345qD對接焊縫在不同溫度條件下屈服強度、抗拉強度以及彈性模量試驗值如表5所示。

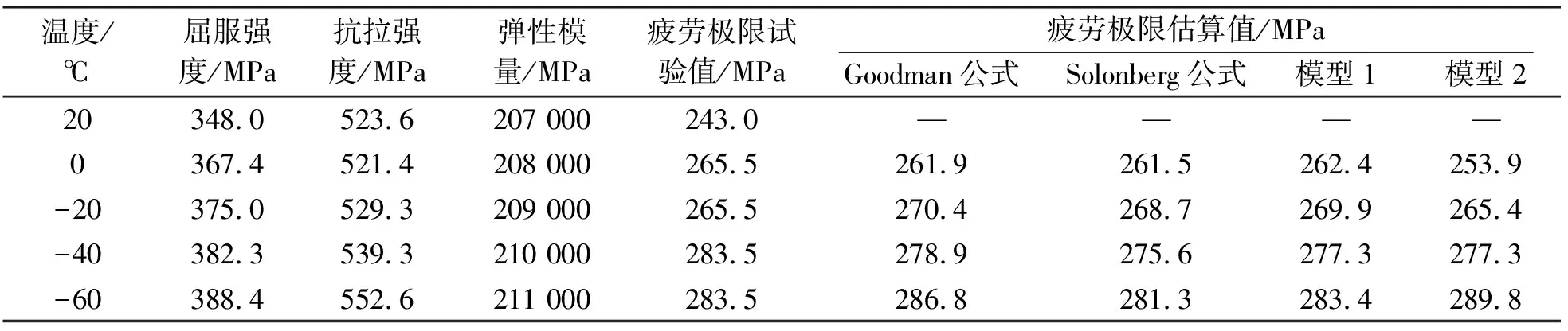
表5 不同溫度下Q345qD鋼材對接焊縫力學指標及疲勞極限值

將表中試驗數據代入式(11)、式(12)和式(13)中，可得到對接焊縫屈服強度、抗拉強度及彈性模量隨環境溫度變化的估算模型。

屈服強度：σy=348exp[0.001 88(20-T)]

(23)

抗拉強度：σb=523.6exp[0.000 48(20-T)]

(24)

彈性模量：E(T)=207 000-50(T-20)

(25)

3.2.2 疲勞極限估算

不同低溫環境下對接焊縫疲勞極限試驗值以及不同模型的估算結果如表5所示。

3.2.3 疲勞壽命估算

根據低溫環境下Q345qD對接焊縫有效初始裂紋、臨界裂紋、疲勞極限等關鍵參量，運用本文提出的改進模型對材料疲勞壽命進行估算，結果如表6、表7所示。

由表6、表7可知：對于Q345qD對接焊縫，在不同低溫環境下，所建的改進模型能夠對該材料的疲勞壽命進行有效的估算，與文獻[5]中模型結果對比，改進模型的估算結果與試驗數據更為接近。

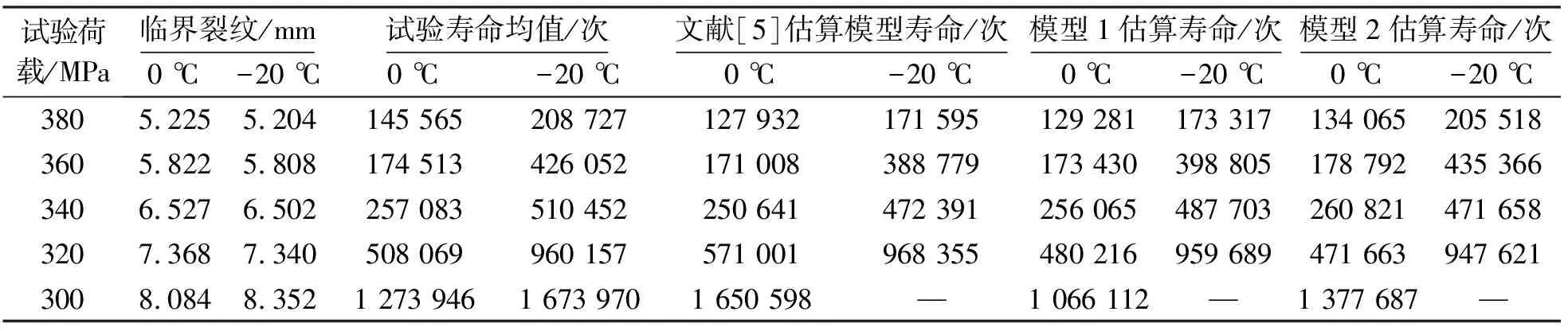
表6 0 ℃和-20 ℃Q345qD鋼材對接焊縫疲勞壽命估算值

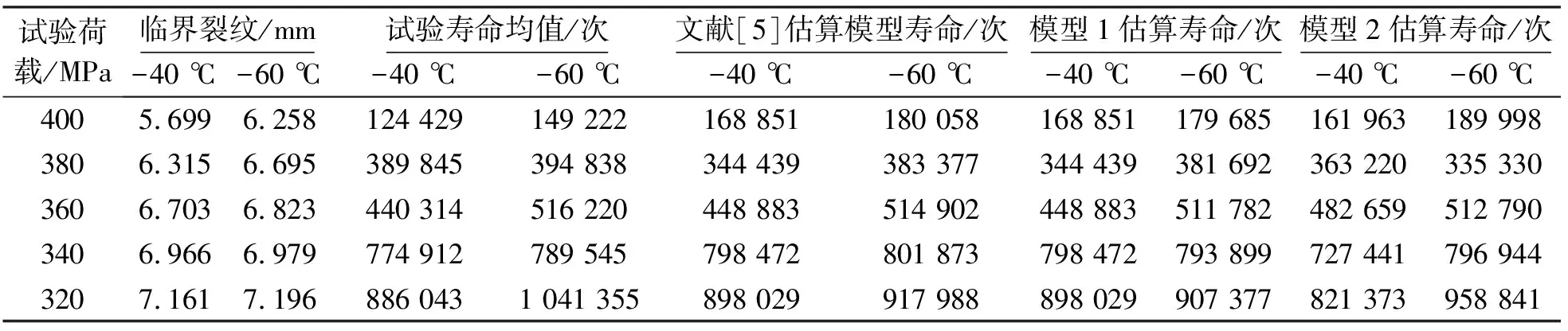
表7 -40 ℃和-60 ℃Q345qD鋼材對接焊縫疲勞壽命估算值

根據上述2個算例可知，隨著環境溫度降低，材料的疲勞極限、裂紋擴展應力強度因子門檻值以及疲勞壽命均有所提高。對低溫環境下的鋼材Q345qD母材和對接焊縫的疲勞性能采用改進模型進行估算，所得到的疲勞極限估算值與試驗值吻合良好；疲勞壽命估算結果與試驗結果較為接近，相較于文獻[5]中的模型，估算精度也有明顯提高，驗證了所建模型的可行性。

4 結論

(1)利用抗拉強度、屈服強度以及環境溫度對材料疲勞極限進行修正，所改進的疲勞壽命估算模型能較好的體現環境溫度對疲勞裂紋擴展速率的影響，并能夠較準確的對低溫環境下材料疲勞壽命進行預測。

(2)根據低溫環境下Q345qD母材與對接焊縫各項試驗數據對比結果，無論是材料疲勞極限，還是疲勞壽命，本文提出的2種改進模型均具有良好的可行性，與文獻模型進行對比，估算精度有所提高，估算結果與試驗結果更接近。

(3)改進的低溫疲勞壽命模型形式較為簡單，僅需兩個參量便可對關鍵參數疲勞極限進行估算，且參數比較容易通過試驗獲得，非常適用于實際低溫環境下工程結構的疲勞壽命估算。