基于Matlab/GUI 的數字圖像邊緣檢測算法研究

魏 林,華康民

(鄭州航空工業管理學院 實驗室與設備管理處,河南 鄭州 450000)

1 傳統數字圖像邊緣檢測算法介紹

邊緣檢測就是找出圖像灰度在某一處發生劇烈變化的位置[1],經典的邊緣檢測算子利用圖像邊緣一階導數極值點和二階導數過零點進行圖像的二值化[2]。利用邊緣檢測算子進行數字圖像的處理過程如圖1所示。

圖1 邊緣檢測過程

1.1 梯度算子

Roberts 算子是最簡單的一階微分算子,利用一階導數峰值檢測邊緣點,通過將2×2 的算子模板帶入計算,分別在垂直和水平方向進行一階導數計算求和,并在圖像對角線方向上相鄰的差值求梯度幅值,所以在水平和垂直方向對圖像檢測精度很高,對噪聲很敏感,同時檢測較為粗糙,邊緣易丟失。

Prewitt 算子為了減少在檢測過程中受到的噪聲影響,該算子模版算子由2×2 變為3×3,這是一種理想情況下的圖像邊緣,用來檢測圖像,得到的梯度幅值最大值作為輸出值。

Sobel 算子與Prewitt 算子類似,都是3×3 的模板,只是在模板方向上不同,而且都是利用方向差分運算與局部運算相結合的方法[3]。 與Prewitt 類似,Sobel 算子在計算的時候體現了很好的方向性,檢測的邊緣都是與模板最類似的點,通過加權平均運算,與卷積算子運算后代入,便可得到圖像的邊緣幅值,然后利用幅值與選定的閾值TH 進行比較,若P(x,y)>TH,則選定該點作為邊緣點,從而完成對圖像的二值化,Sobel 算子對圖像的檢測體現較好的方向性,也更加與模板檢測點趨同。

1.2 基于二階導數的邊緣檢測算子

Laplace 算子利用圖像邊緣剖面二階導數過零點的特性進行邊緣檢測,Laplace 算子在運算過程中作為一個標量,在具有等斜率的寬區域上,有可能將全部區域都當作邊緣檢測出來[4]。 在沒有噪聲干擾的情況下,Laplace 算子檢驗時表現出方向的丟失,在加入噪聲的情況下,邊緣嚴重丟失,對噪聲非常敏感。

Log 算子在檢測過程中,首先進行噪聲的去除,然后再利用差分算子進行運算找出圖像邊緣。 在求二階導數之前先進行平滑濾波,一般認為加性噪聲服從正態分布,針對這一點選擇高斯平滑濾波器進行去噪[5],再利用Laplacian 銳化濾波器進行處理,從運算的結果零交叉來得到圖像的邊緣信息,這種算子的特點就是對圖像的抗噪性能較好。

Canny 算子邊緣檢測的方法是尋找圖像梯度的局部最大值,Canny 算子設定了兩個閾值,并分別檢測出強邊緣和弱邊緣,而且僅當強邊緣和弱邊緣相連時,弱邊緣才會包含在輸出中[6]。

2 特定閾值對邊緣檢測實驗分析

2.1 特定閾值實驗

該實驗對于一階導數的實驗,有默認閾值和獲取外部閾值兩種方式,并可選取方向,對于二階導數的試驗有默認閾值和獲取外部閾值兩種方式,并結合標準差對圖像進行檢測,在Matlab 中edge 函數用于對灰度圖像進行邊緣提取,返回的是與讀取圖像大小一樣的二進制圖像BW,語法如下:BW=edge(I,‘method’,thresh,directions,sigma),本文設計的基于Matlab/GUI的圖像邊緣檢測系統即將edge 函數內置到系統中,通過編程呈現可視化的界面實時進行檢測。

在一階算子中采用的都是算子模板,通過計算得到梯度之后,與默認閾值或外部閾值相比較,再對圖像二值化,就可以得到檢測后的圖像。 下面就只針對默認閾值,在二階算子中,Laplace 算子由于在edge 函數中不能被運用,所以本實驗用的是它的算子模板,利用graythresh 函數,計算的是一個全局閾值,在使用im2bw函數將灰度圖像轉換為二值圖像時,這種通過系統自動計算的閾值被稱作默認閾值,而其他算子都通過edge 函數來計算。

上述對圖片采用的是默認閾值,而且對于一階算子采用的都是both 方向,從實驗結果也可看到閾值,檢測同一圖片的默認閾值如表1 所示。

表1 檢測同一圖片的默認閾值

根據以上默認閾值,設定3 個在此范圍段的閾值,分別為0.005,0.05,0.1。 下面就同一幅圖片,一階算子方向為both 下,二階算子的標準差均為2,在不同閾值的不同算子之間的圖像效果對比來探究實驗結論。

2.2 特定閾值實驗分析及結論

通過實驗從橫向和縱向分別來對比圖像在不同閾值下的變化規律。 首先,從橫向對比,同一閾值下的各算子在處理圖像時表現出個體差異,當閾值為0.005時,Log 算子檢測的圖像邊緣最佳,且細節也較豐富,而對于其他算子檢測邊緣都很不清晰,對于Log 算子當閾值大于0.005 時,圖像幾乎看不到,說明該算子對較小閾值敏感。 Canny 算子檢測的圖像相對而言圖像細節更豐富,方向感更好,也體現出來Canny 算子是一種較優的檢測算子。 縱向對比,可發現對同一算子閾值越小,圖像邊緣越清晰,細節越豐富,反之,閾值越大,邊緣丟失越嚴重,可看出閾值越小,檢測的邊緣越雜亂且豐富,當增大閾值后,圖像邊緣開始變得不清晰,當閾值為0.1 時,邊緣已經幾乎不見。 二階算子利用二階導數過零點檢測圖像在檢測過程中檢測效果要優于一階算子,在存在噪聲干擾時,一階算子對噪聲較為敏感,因此一種好的邊緣檢測算法要具有較強的抗噪性。

3 標準差對于邊緣檢測算子的實驗分析

3.1 實驗仿真結果

在Log 算子和Canny 算子檢測邊緣的時候,第一步往往都是通過高斯濾波器先除掉噪聲,那么在高斯函數中,Sigma 作為其標準差,決定了去噪的效果,通過對Log 算子和Canny 算子在各種不同的Sigma 值下的檢測圖像對比得出結論,如圖2—5 所示。

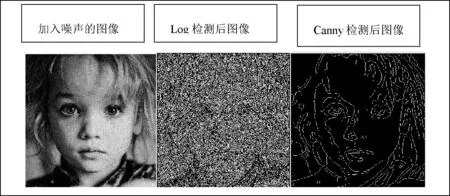
圖2 Sigma=1 時的Log 和Canny 算子檢測

圖3 Sigma=2 時的Log 和Canny 算子檢測

圖4 Sigma=3 時的Log 和Canny 算子檢測

圖5 Sigma=4 時的Log 和Canny 算子檢測

3.2 實驗分析及結論

從實驗結果對比可以看出,標準差的大小決定抑制噪聲的效果,從Log 算子的圖像縱向比較來看,Sigma的值越大,對相應圖像的去噪效果越好,從圖4 可以看出,當Sigma=3 時,噪聲已經不存在,但當繼續增大標準差時會發現,圖像的邊緣信息開始丟失。 可以看出標準差有平滑圖像邊緣的作用,在一定范圍內,標準差的值變大,平滑效果越好,但同時圖像邊緣丟失也越來越明顯。

但從Canny 算子檢測的效果圖來看,對于不同的算子,其標準差的選取不太一樣,Canny 算子比Log 算子有更好的對標準差的適應性,在標準差上的選取上有一個較大的選取空間,而且效果要比Log 算子好,檢測的輪廓更清晰,且邊緣更豐富。

4 幾種算子的改進及實驗分析

4.1 改進方法

為了增強Sobel 算子其在各方向上的敏感度,改進的算子提出了增加其方向模板的方法,分別在0°和90°的基礎上增加45°,135°,180°,225°,270°,315°方向上的模板,來進行卷積運算。

從以上實驗可以看出,傳統的Laplace 算子邊緣檢測過程中,方向丟失而且由于是雙倍加強了圖像對噪聲的敏感,檢測出圖像的邊緣不連續,在已有的算法中,所用的模板是8 個方向的,分別是0°,45°,90°,135°,180°,225°,270°,315°在此基礎上增加8 個方向模板,分別為22.5°,67.5°,112.5°,157.5°,202.5°,247.5°,292.5°,337.5°,并改變模板中的參數,更改的目的就是能夠更精確地檢測邊緣。 下面就針對改進過后的算法帶入檢測系統,實驗仿真如圖6—7 所示。

圖6 Sobel 算子改進前后檢測

圖7 Laplace 算子改進前后檢測

4.2 實驗分析

從以上實驗結果分析對比可以看出,改進后的Sobel 算子首先對圖像邊緣的連續性控制得更好;其次對圖形的噪聲去除效果更強;最后,圖像的精細程度明顯好于改進前,因此可以看出改進后的Sobel 算子具有一定的優越性。

對于Laplace 算子,從前后實驗結果圖對比可以看出,改進之后的Laplace 算子由于在模板上增加了8 個方向,而且參數也更小,這樣檢測的圖像可以看到如果沒有噪聲干擾,能夠得到很好的檢測結果,也避免了方向的丟失,可以提高邊緣檢測的精度,同時又合理地設置了參數,因而避免了一些偽邊緣的提取[8]。

5 結語

本文通過基于Matlab 的GUI 開發出來了一個可視化的圖像處理界面,簡單易懂,能夠非常清晰地反映出檢測前后的圖形對比情況,把Roberts,Prewitt,Laplace,Log,Canny 經典的算子在應用模塊中得到了實現,并研究了在一定閾值和標準差下圖像的變化規律,并實現了在加入噪聲之后圖像的變化對比,檢測的最終目的是抑制噪聲、定位準確和低重復響應,從復雜煩瑣的實驗結果中找出差異,進行橫向、縱向對比,最后提出了對Laplace 算子和Sobel 算子模版的幾點改進意見,并得到了實現。 總體來看,邊緣檢測算子還有很多領域亟待研究,未來在算法改進方面應加強對噪聲的抑制和通過特定閾值并加入多個方向來控制精細邊緣輸出,并針對不同類型的圖片提出特定的算法解決方案。