超空泡航行體高速入水空泡與載荷特性數值分析
魚怡瀾, 施瑤, 潘光, 車沛锜
(1.西北工業大學 航海學院, 陜西 西安 710072;2.西北工業大學 無人水下運載技術重點實驗室, 陜西 西安 710072)
超空泡航行體通過在水下航行時產生包裹航行體的超空泡來減少航行體沾濕面積,使航行體所受阻力大幅降低,隨著現代戰爭對水下武器快速性要求的提高,超空泡航行體的應用需求與日俱增。同時,為增大航行體航速與航深,需要發展更高效的發射平臺,空投方式相比于水面艦艇或水下潛艇投放有攻擊時間短、命中率高的優點。但空投航行體高速入水瞬間氣、水、航行體發生瞬時強烈流固耦合作用,航行體承受瞬時極端載荷,流場出現復雜湍流流動與渦旋現象,可能引發航行體結構斷裂、連接失效、彈道失穩等,直接影響著航行體入水的結構安全、彈道穩定以及航行體入水后產生的超空泡,從而影響航行體航行質量。因此,捕捉空泡界面演變規律,預報載荷峰值脈寬等對提高航行體速度、保證航行體安全入水有重要意義。
目前已有的超空泡航行體相關研究對象主要為速度低于100 m/s的圓柱體、楔形體、小球入水和直徑小于0.01 m的射彈。其中,理論研究大多將問題簡化處理,只能用于解決簡單問題;實驗研究中水洞實驗不關心入水過程[1-3],高速射彈實驗[4-5]由于設備條件限制很難將入水速度提高至100 m/s以上量級;數值仿真方法隨著計算機技術的發展逐漸成為研究入水問題的重要手段[6-11],但目前對于高速超空泡航行體入水問題的研究仍然較少,而航行體高速入水問題的空泡流場更復雜、載荷與速度平方成正比,因此小型低速入水問題的結論不具備普適性,急需開展相關研究。
入水速度V與入水角度θ是影響空泡與載荷特性的重要因素,本文建立了適用于超空泡航行體以100~300 m/s速度高速入水的數值模型,分析了入水速度與入水角度對入水空泡與載荷特性的影響,為超空泡航行體高速入水相關研究提供參考。
1 數值計算模型
本文使用FLUENT進行數值模擬,將航行體視為剛體,考慮水的壓縮性,采用RANS模型、VOF多相流模型、標準k-ε湍流模型和Zwart-Gerber-Belamri空化模型建立了航行體高速入水數值計算模型,并通過UDF(user defined function)實現航行體六自由度運動。
1.1 控制方程
流體的運動遵循質量守恒定律、動量守恒定律和能量守恒定律,因而可以通過這3個定律建立流體的控制方程組。本文使用雷諾平均N-S方程方法,該方法將瞬時運動分解為脈動運動和平均運動2項,是目前應用最廣泛的方法,其具體方程為:
1) 連續性方程:
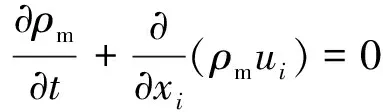
(1)
2) 動量守恒方程
(2)
3) 能量守恒方程
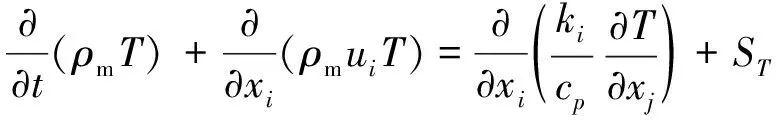
(3)
式中:u為速度;ρm為混合物的密度;μm為混合物動力黏度。
1.2 湍流模型
為了使控制方程封閉,選擇標準k-ε湍流模型,該模型適用范圍廣,收斂性好。其中,湍動能k的輸運方程為
(4)
湍流耗散的輸運方程為
(5)
1.3 多相流模型
對于存在多相流動的問題需要使用多相流模型,VOF模型適用于存在互不相融的流體的交界面的情況,因此本文使用VOF多相流模型,設置空氣相為主相,液體為第二相,水蒸汽為第三相,通過求解單元內的值判斷其相分布,滿足
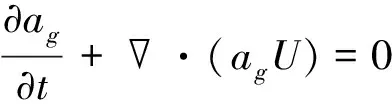
(6)
式中:ag=0時,該控制單元內無空氣;ag=1時,該控制單元內全為空氣;0 本文由于航行體高速入水存在空化現象,因此使用了Zwart-Gerber-Belamri空化模型,該模型基于Rayleigh-Plesset方程,其控制方程為 (7) 式中:氣泡半徑RB為1×10-6m;αnuc為汽化核心體積分數;汽化系數Fvap為50;凝結系數Fcond為0.001;pv為飽和蒸汽壓力。 氣相和水相的狀態方程為控制方程提供了封閉條件。其中水相采用Tait狀態方程,表示為 (8) p0和ρ0是參考溫度T0下的參考值。K0和n是溫度和壓力的弱函數,通常假定它們為常數,分別是3×108Pa和7。 此外,將水蒸汽相和氣相近似為理想氣體 p=ρgRT (9) 式中:R為氣體常數;ρg為氣體密度。 航行體模型如圖1所示,模型分為頭部圓盤空化器、錐段、圓柱段,以空化器前端面圓心為坐標原點,航行體質量為M,總長為L,直徑為D,質心距空化器端面距離為L1,空化器直徑為D1,厚度為H,各尺寸如表1所示。 圖1 航行體模型示意圖 表1 航行體參數 計算域如圖2所示,為長方體計算域,水域尺寸為27 m×27 m×40 m,空氣域為27 m×27 m×10 m,坐標原點距左側壁10 m。計算域上方為壓力出口,其余均為壁面。航行體初始位置距水面0.01 m,地面坐標系原點位于航行體軸線與水面交點,入水角為航行體軸線與水平面所夾銳角。 圖2 計算域示意圖 本文使用重疊網格方案計算,背景域為六面體網格并加密航行體路徑,重疊網格區域使用非結構化網格,兩者交界處網格尺寸相同,網格如圖3所示,總網格量約為8×106。 圖3 網格示意圖 為驗證數值方法的準確性,在西北工業大學無人水下航行器重點實驗室進行了實驗驗證,實驗模型直徑為0.02 m,質量為10.8 kg,入水角度為45°,入水速度為100 m/s,實驗裝置示意圖如圖4所示,主要由空氣炮發射、數據采集和高速攝像裝置等組成,通過高壓氣體推動航行體加速。數據采集裝置主要由加速度傳感器、數據存儲模塊、數據解析軟件等組成,高速攝像裝置由空中高速相機、水下高速相機和水下照明燈等組成。圖5為9 ms和18 ms時實驗與數值計算空泡對比圖,可得本文使用的數值計算方法和實驗結果吻合較好,建立的數值模型可靠。 圖4 實驗裝置示意圖 圖5 空泡輪廓對比圖,左:實驗,中:仿真 本文子域網格量為背景域網格量的20倍,因此通過改變overset邊界的網格尺寸改變網格量。選擇其尺寸為50,60,100,140 mm,計算入水角為90°、入水速度100 m/s時航行體速度變化與加速度變化,結果如圖6~7所示,綜合考慮計算資源與計算效率之后選擇使用overset尺寸為100 mm的網格計算。 表2 網格方案 圖6 不同網格尺寸下航行體速度隨時間變化曲線 圖7 不同網格尺寸下航行體加速度隨時間變化曲線 圖8為航行體以速度100 m/s、角度60°入水的空泡演變圖。可得航行體入水過程中空泡經歷了產生、膨脹、閉合、收縮4個階段。 在空泡產生階段,航行體高速撞擊水面,使自由液面流動發生分離,將水排開使空氣進入水中;在空泡膨脹階段,空化器周圍空泡壁面持續擴張,隨著航行體入水深度增大,更多的空氣進入水中,空泡長度逐漸增大;在空泡閉合階段,首先空泡閉合在航行體上,使航行體表面沾濕,其次隨著航行體入水深度增大,空泡長度增大,內部壓力降低,流體對空泡的壓力使空泡發生頸縮直至發生深閉合;在空泡收縮階段,空泡分為上下兩部分,上部分空泡逐漸向水面收縮直至閉合,下部分空泡隨航行體運動,隨著航行體入水深度增大持續收縮。 整個入水過程中航行體將自身動能轉化為流場勢能,流場將勢能轉化為水的動能,使流體從高壓區流向低壓區,同時使空泡演變。 圖8 入水空泡形態隨時間演變圖 如圖9所示,空泡最大直徑dmax為航行體產生空泡的最大直徑。圖10為不同入水條件下空泡最大直徑,可得隨著入水速度增大,空泡最大直徑增大,原因為速度增大使航行體動能增大,使液體流速增大,空泡擴張速度增大;隨著入水角度的增大空泡直徑變小。其中 λ=dmax/2D (10) 圖9 空泡最大直徑定義圖 圖10 空泡最大直徑變化曲線 圖11 不同速度下空泡隨時間演變圖(θ=90°) 圖11為入水角度90°,入水不同速度入水空泡圖,由圖可得隨著速度增大航行體空泡出現閉合的位置深度增大。原因為速度增大使動能增大,空泡中壓力降低的速度變慢,因此空泡被夾斷的時間推遲。 圖12為100 m/s入水270 ms空泡輪廓圖,4個入水角度下都發生了空泡深閉合,且發生深閉合時航行體航行距離相同,因此入水角度對空泡深閉合無影響。 圖12 入水270 ms空泡輪廓圖(V=100 m/s) 圖13為不同角度入水加速度變化圖,圖中速度100 m/s下加速度出現2次峰值,第一次峰值是航行體入水瞬間沖擊造成,在此處隨入水角減小航行體頭部與水面的接觸面積減小,加速度相應減小。第二次峰值是由于空泡閉合在航行體上,使航行體表面沾濕,在此處隨入水角減小加速度增大。 隨著入水速度增大加速度峰值增大,出現時間提前,原因為速度增大使航行體動能增大,入水瞬間向周圍的水傳遞的能量增大。 圖13 加速度隨時間變化曲線 為了使模型所描述的規律獨立于量綱的影響,通常需要使用無量綱量來描述客觀規律,因此將軸向載荷F通過(11)式無量綱化為軸向載荷系數Cd Cd=F/(ρwπD2V2) (11) 式中,ρw為水的密度,取1 000 kg/m3。 圖14為不同角度入水時航行體軸向載荷隨時間變化圖,由圖可得隨著入水速度增大,軸向載荷峰值增大,出現時間提前。其原因為速度增大使航行體動能增大,向自由液面傳遞的能量增大。 隨著入水角度減小,航行體受軸向載荷峰值逐漸減小。其原因為隨著入水角減小航行體動能水平分量增大,垂直分量減小,兩者軸向分量之和減小。 圖14 入水軸向載荷系數Cd隨時間變化曲線 圖15為100 m/s,60°入水部分時刻壓力云圖,可得入水時空化器迎流面首先出現壓力峰值,其次錐段出現峰值,之后航行體尾部及空泡深閉合處出現壓力峰值,最后隨著時間增大壓力峰值面積增大且逐漸關于航行體軸線對稱。 圖15 不同時刻壓力云圖(V=100 m/s,θ=60°) 航行體表面壓力峰值出現在觸水區域,速度高于150 m/s時空泡包裹航行體,壓力峰值只出現在空化器上,因此進一步研究空化器周圍壓力分布,設置了壓力監測點如圖16所示,其中r為空化器半徑。 圖16 監測點分布示意圖 圖17為200 m/s不同角度入水監測點壓力隨時間變化圖,可得被空泡包裹的點4,5壓力近似為0,遠小于空化器迎流面壓力;空化器表面點3,6的壓力值小于點1,2,7,即空化器迎流面的壓力越接近圓心越大;斜入水時,點3和點6的壓力差較大,點2和點7的壓力差較小,即空化器迎流面壓力分布不對稱,隨著入水角度的減小不對稱現象加劇,且沿著半徑向圓心方向減弱。 圖17 各監測點壓力隨時間變化曲線(V=200 m/s) 本文開展了超空泡航行體不同入水速度和入水角度下入水過程數值仿真,獲得航行體空泡演變、尺寸、載荷及壓力變化規律,獲得結論如下: 1) 隨著入水速度增大,空泡閉合位置的深度增大,空泡最大直徑增大;隨著入水角減小空泡最大直徑增大,深閉合發生時間不變。 2) 100 m/s和150 m/s速度入水出現2次加速度峰值,隨著入水速度增大加速度峰值增大;隨著入水角減小,加速度第一次峰值減小,第二次峰值增大。 3) 隨著入水速度增大,航行體軸向載荷峰值增大,出現時間提前;隨著入水角度減小,軸向載荷峰值減小。 4) 入水過程中空化器迎流面壓力沿著半徑向圓心方向增大,但斜入水時的不對稱現象減弱。1.4 空化模型
1.5 狀態方程
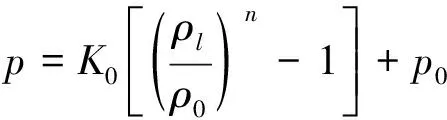
2 計算模型與網格
2.1 航行體模型
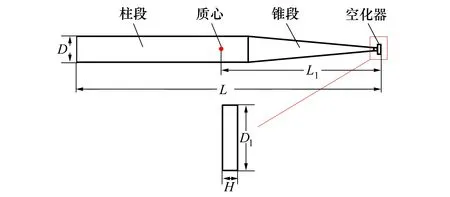

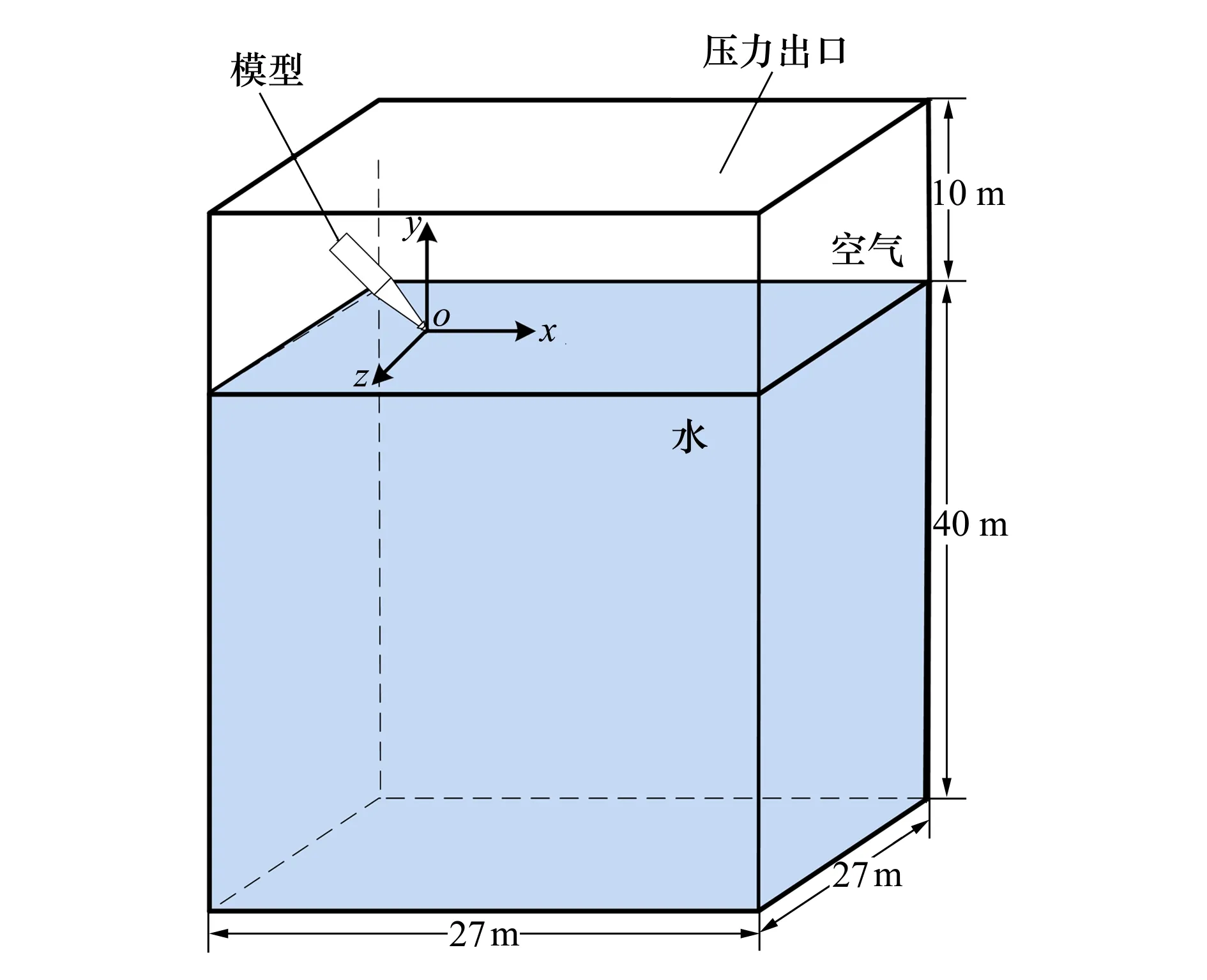
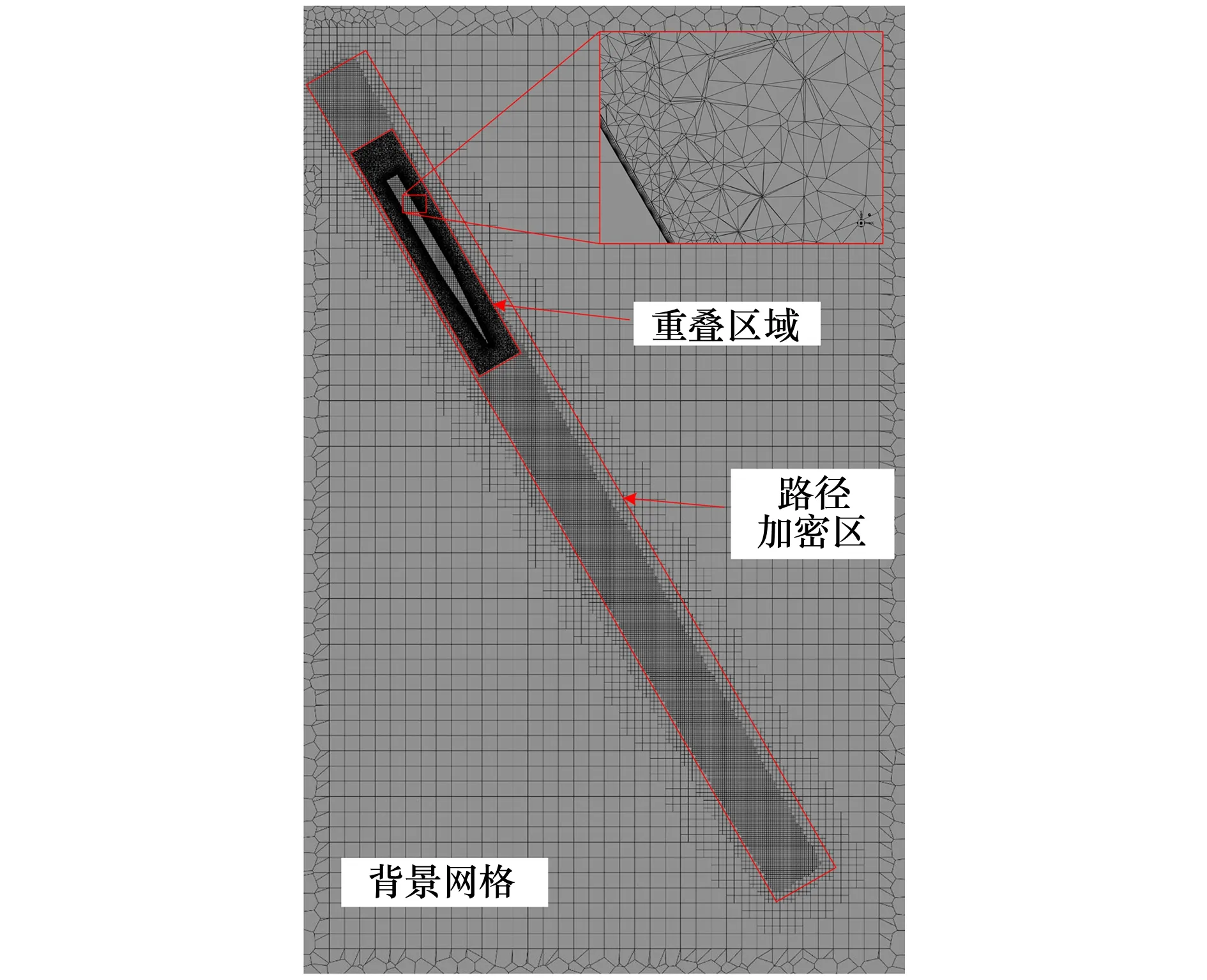
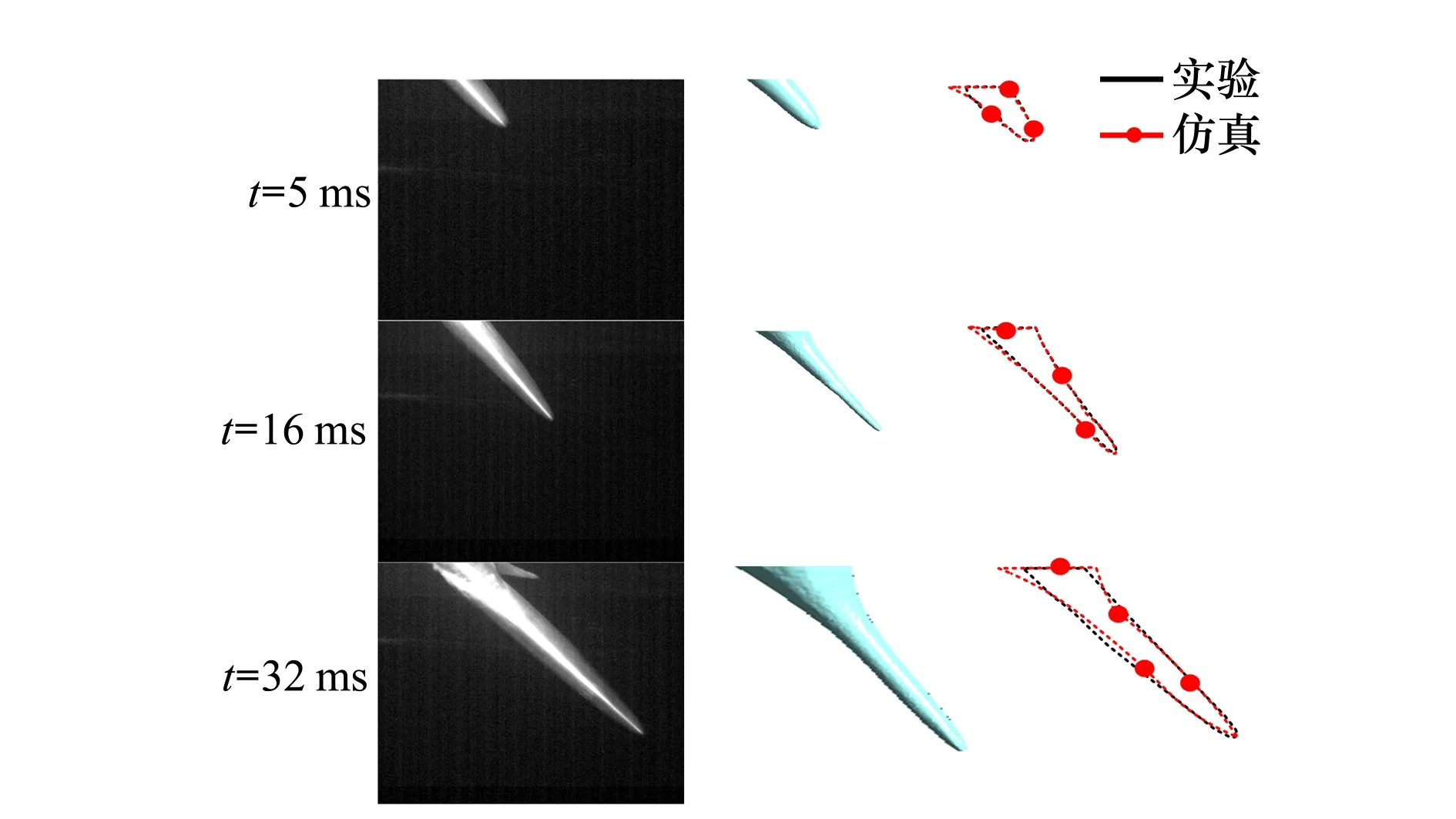
2.2 數值方法驗證
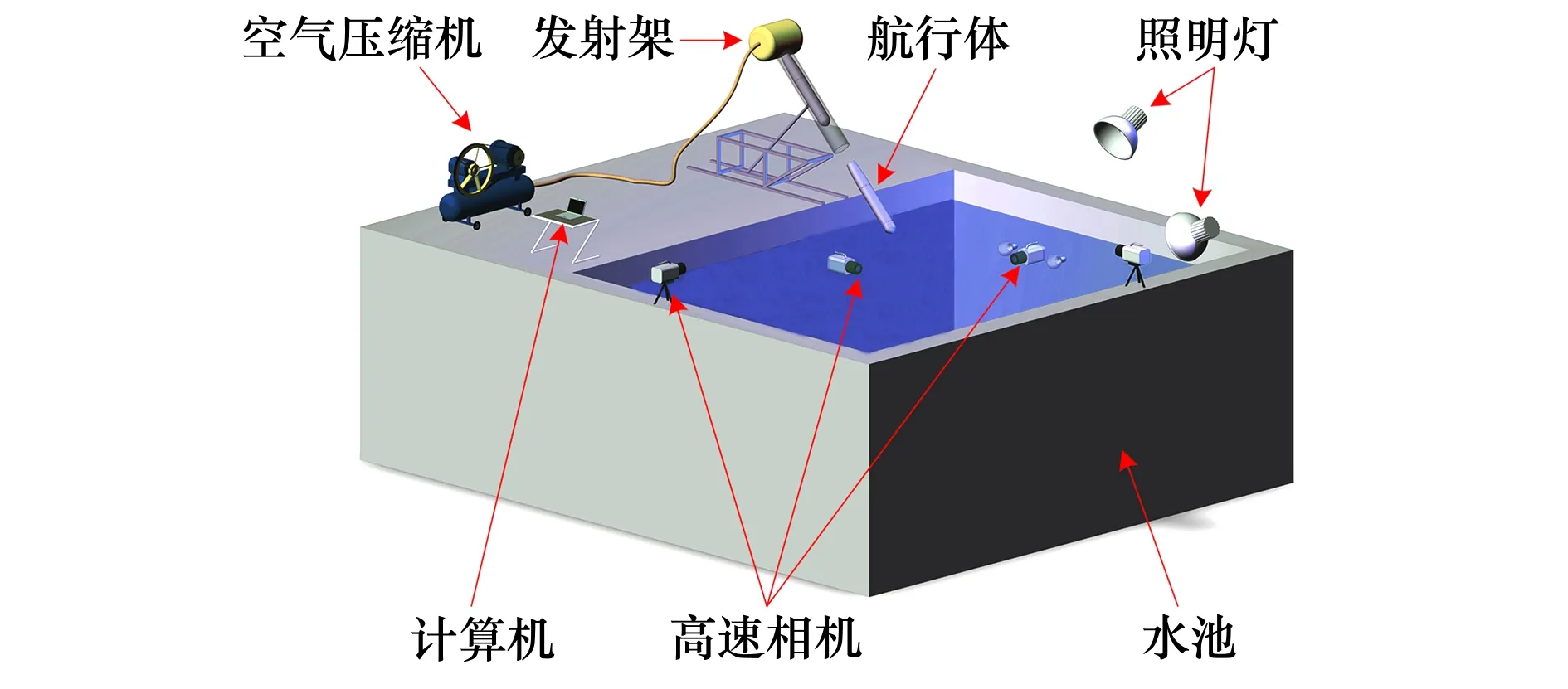
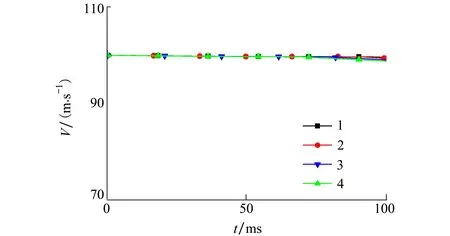
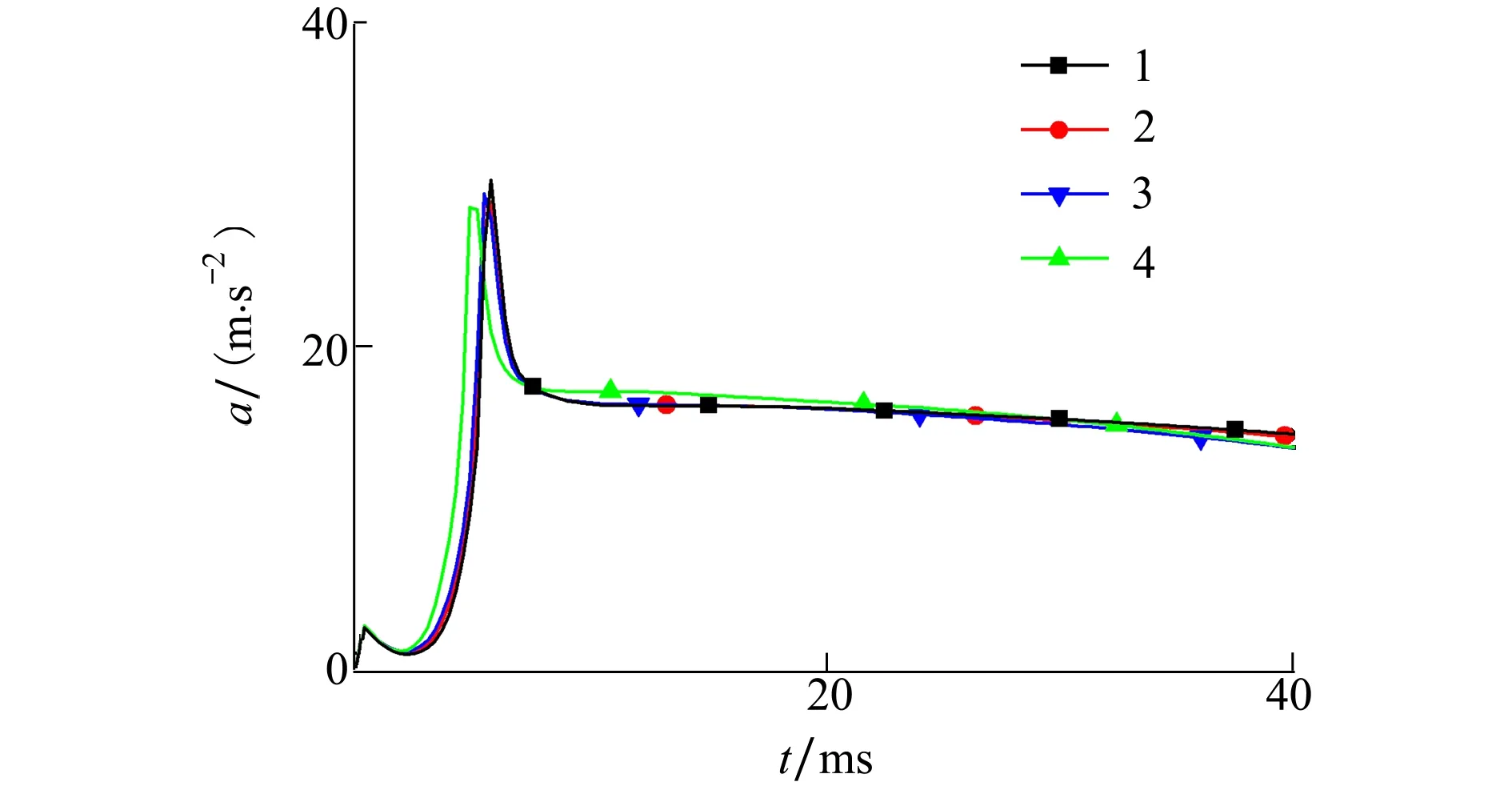
2.3 網格無關性驗證

3 計算結果及分析
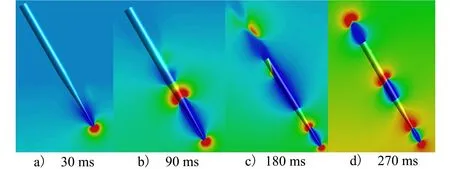
3.1 空泡特性研究
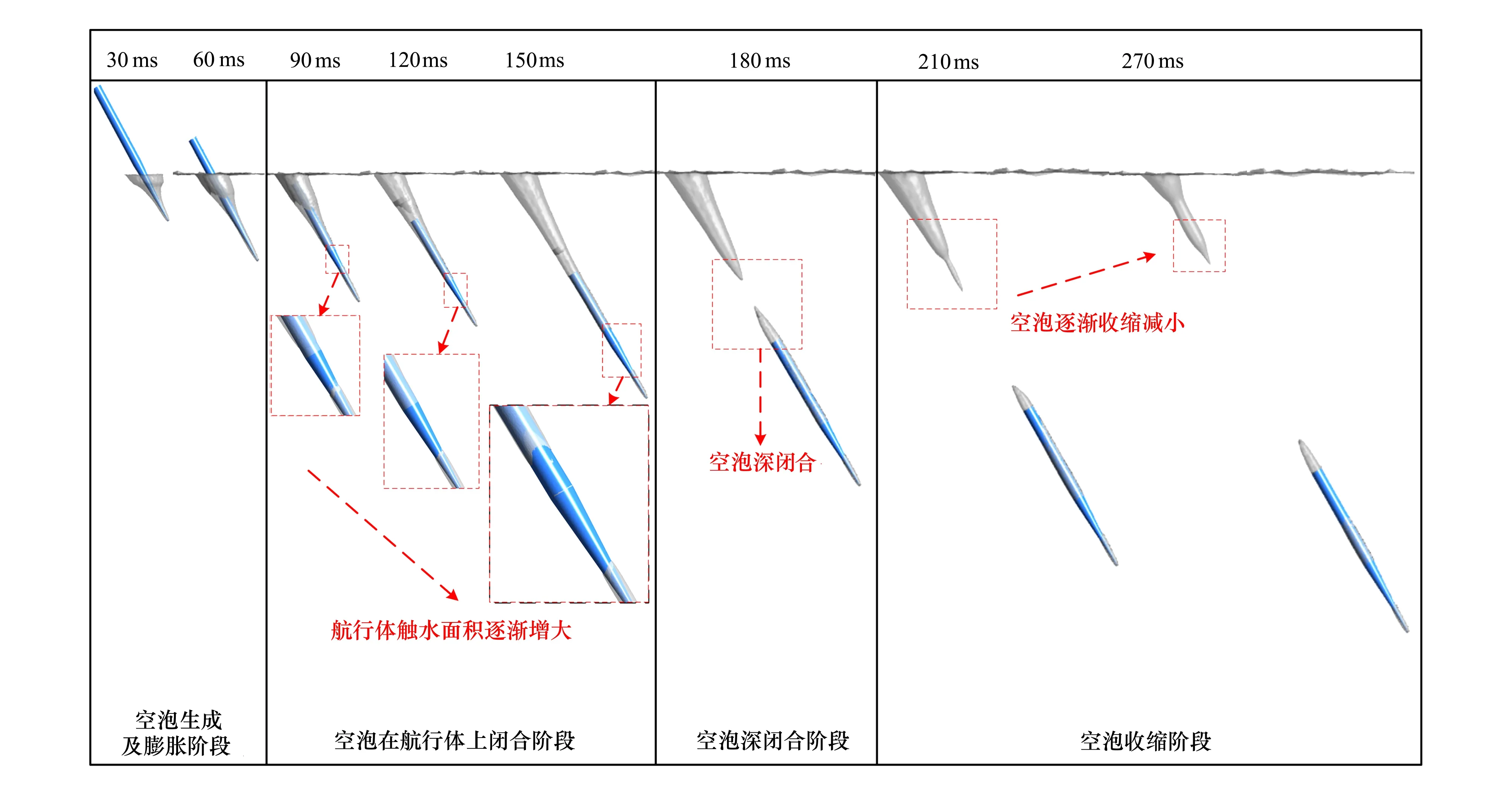
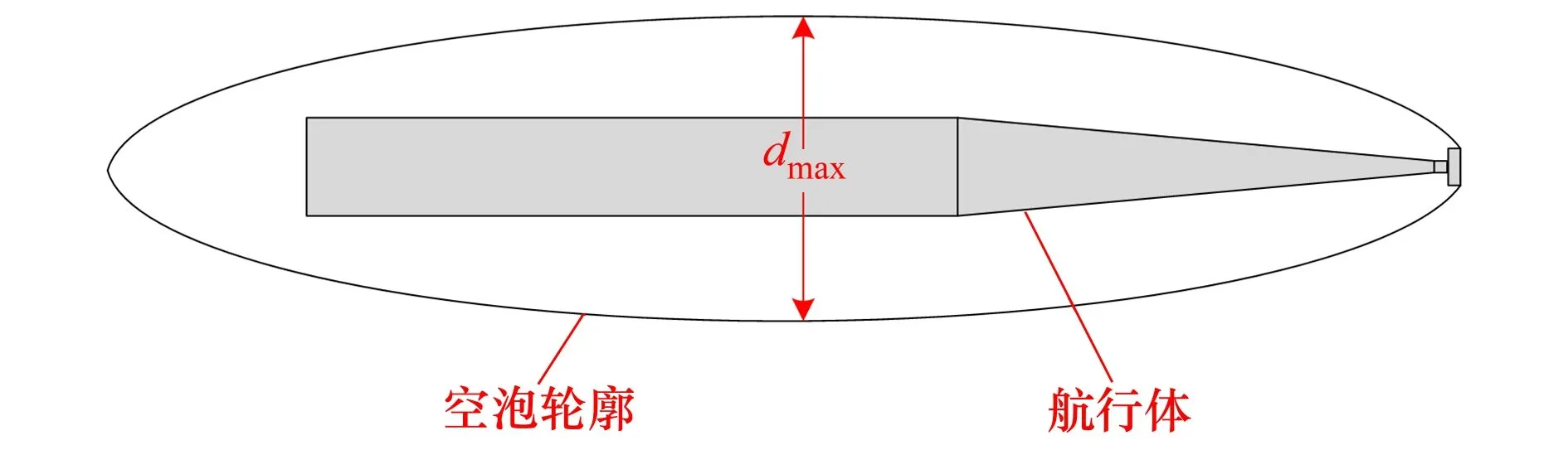
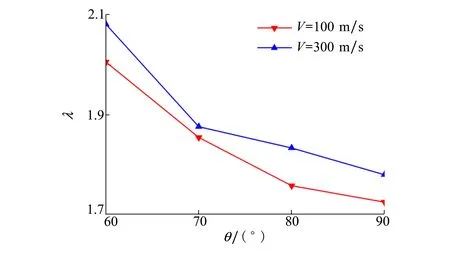

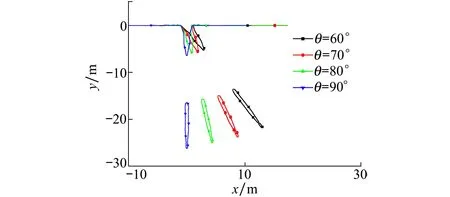
3.2 不同角度下載荷特性研究
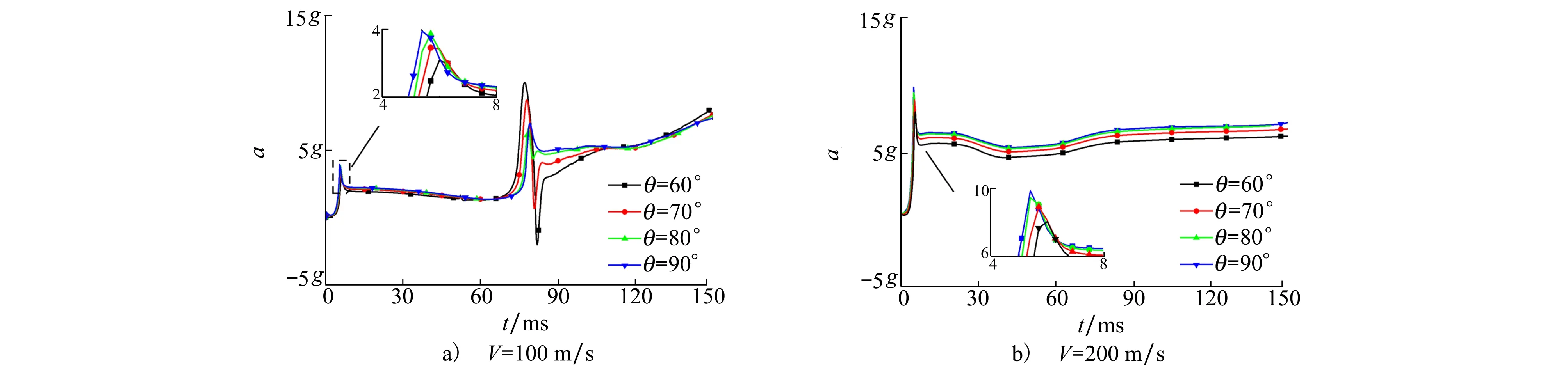
3.3 不同速度下載荷特性研究
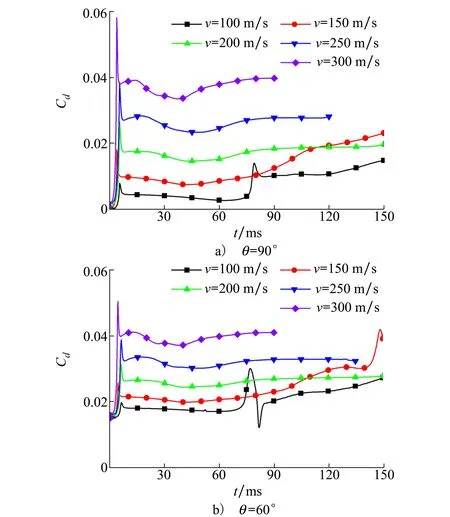
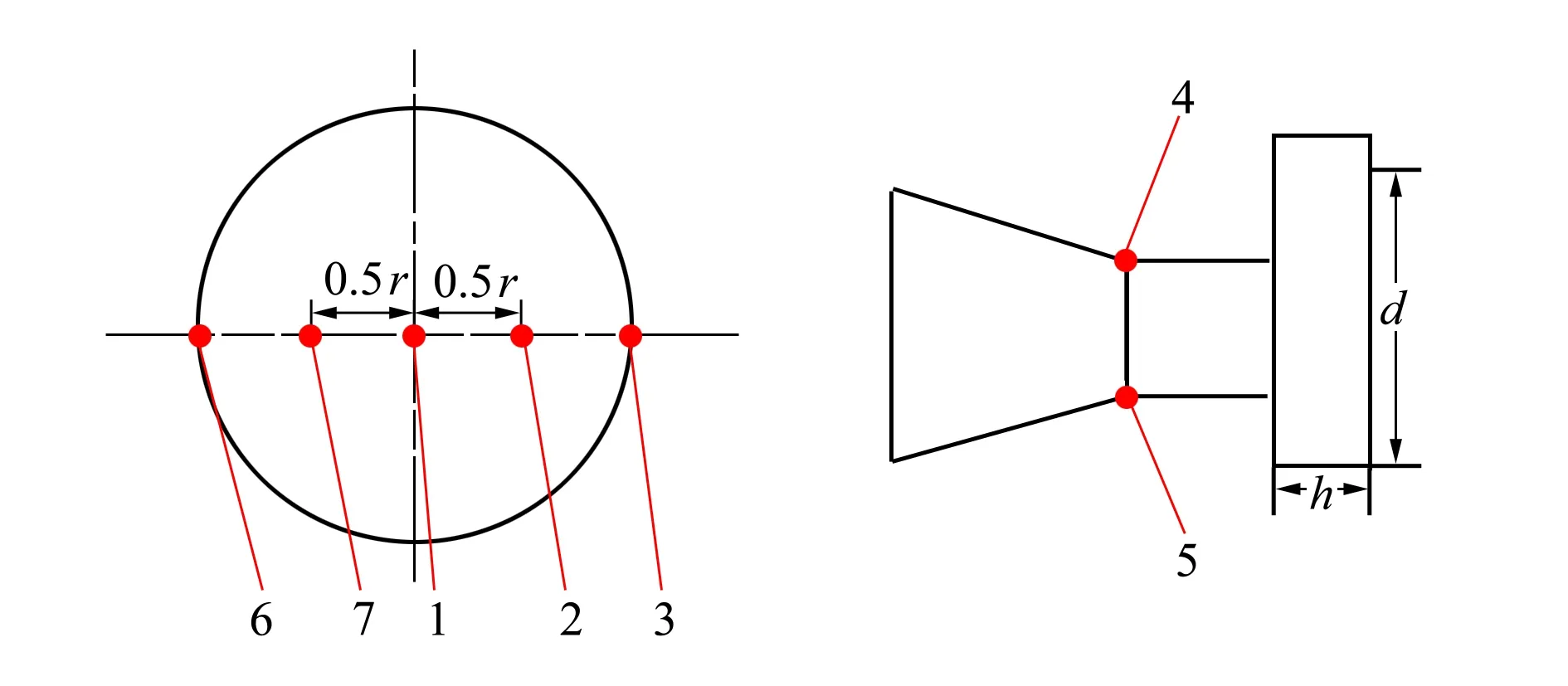
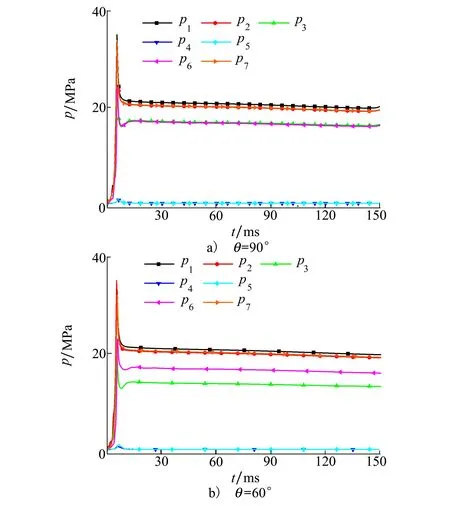
3.4 壓力特性
4 結 論

