推陳出新 培養學生的創新思維
■ 武漢市第三中學 彭愛國
創新思維是指以新穎獨創的方法解決問題的思維過程,通過這種思維能突破常規思維的界限,以超常規甚至反常規的方法、視角去思考問題,提出與眾不同的解決方案,從而產生新穎的、獨到的、有社會意義的思維成果。隨著社會的快速發展,創新人才越來越受到社會的青睞,創新人才的培養也是國家進步和發展的需要。物理是一門以實驗為基礎的自然科學,它是發展最成熟、高度定量化的精密科學,物理學的發展有力地促進了人類文明的進步,高中物理的學習對提高學生的創新思維能力起著積極的推動作用。
在高中力學問題中,整體法、隔離法、正交分解法、合成法、圖解法等這些基本方法可解決大量的力學問題,但是這些常規方法在解決有些問題時會有較大的難度,因而需要我們推陳出新,突破常規思維的界限,培養學生的創新思維,利用所學的基本知識創造性地去解決這些問題。
在涉及到轉動輕桿對固連物體的彈力作用時,很多情景下因桿對物體彈力的大小和方向在不斷變化,用常規方法很難解決。但如果我們能創新應用基本的物理方法,就可很巧妙的解決問題。下題是筆者在教學過程中發動學生一題多解,推陳出新,由學生提出的三種解法,在此與各位同行分享。
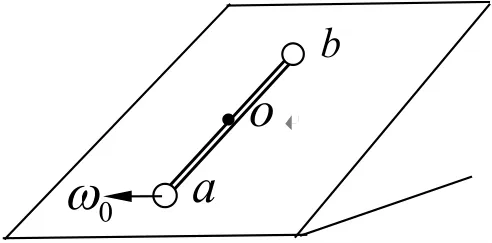
A.在輕桿轉過1800的過程中,角速度先減小后增大
B.只有ω0大于某臨界值,系統才能做完整的圓周運動
C.輕桿受到轉軸的彈力的大小始終為2mgsinθ
D.輕桿受到轉軸的彈力的方向始終在變化
分析與解:當桿繞O點轉過任一α角時,對于小球a、b及桿組成的系統,所受外力的合力矩即為a、b小球重力下滑分力對O點產生的力矩之和,顯然a、b小球重力下滑分力對O點產生的力矩之和為零,即系統勻速轉動。所以A、B錯誤。
對于C、D選項的判斷,學生給出了以下三種解法:
方法一:矢量運算法
醫院總務處進行的綜合節能魚骨圖分析就展現了思考的細致程度。分析將綜合節能劃分為四大路徑,分別是重點用能單元節能降耗、管理節能、可再生能源使用以及更換老舊設備、使用節能產品。
對于處于任意位置的a、b小球及桿組成的系統,由牛頓第二定律有:
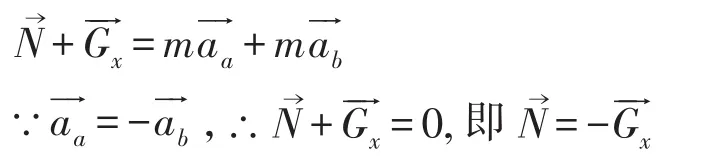
即輕桿受到轉軸的彈力的大小N=2mgsinθ,方向沿斜面向上。C選項正確。
方法二:非正交分解法
將a、b小球所受桿的彈力沿斜面方向和沿桿方向分解,如圖,沿斜面方向的分力分別為Fa1、Fb1,沿桿方向的分力分別為Fa2、Fb2,即有:
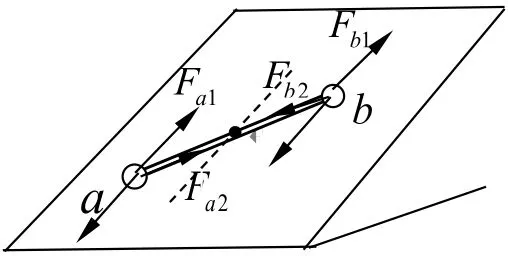
Fa1=Fb1=mgsinθ,Fa2=Fb2=mω02R
對輕桿受力分析如圖,由牛頓第三定律:
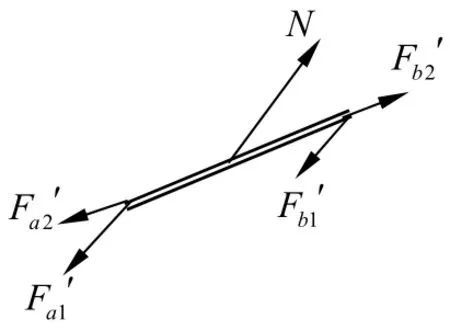
Fa1′=Fa1=mgsinθ,Fb1′=Fb1=mgsinθ
Fa2′=Fa2=mω02R,Fb2′=Fb2=mω02R,沿桿向合力為零
則:N=Fa1′+Fb1′=2mgsinθ,方向沿斜面向上。C選項正確。
方法三:矢量圖疊加法
設小球a、b的重力沿斜面方向的分力分別為Gax、Gbx,輕桿對球的作用力分Fa、Fb,
小球a、b在斜面內受力的矢量三角形如圖(垂直于斜面俯視圖):
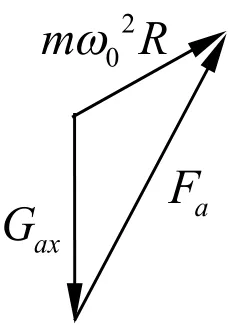
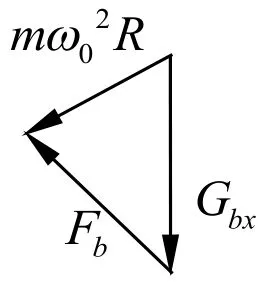
將兩矢量圖平移疊加可得桿對小球的作用力Fa、Fb的合力F=Gxa+Gxb=2mgsinθ,方向沿斜面向上。
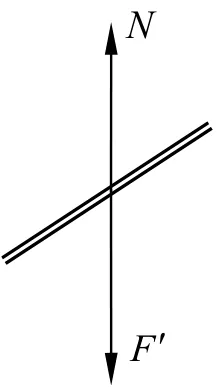
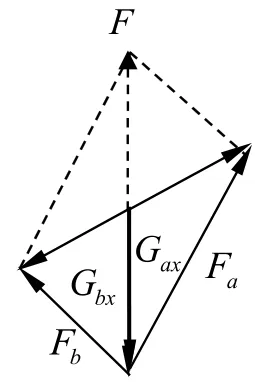
對輕桿有:N=F′,而F′=F=2mgsinθ
即輕桿受到轉軸的彈力的大小N=2mgsinθ,方向沿斜面向上。C選項正確。
方法一避開了列繁瑣的牛頓第二定律分量式方程組及解方程組的復雜過程,巧用矢量式方程,再利用,輕松解決問題,體現了物理規律大道至簡的屬性。
方法二跳出常用的正交分解法的梏桎,根據具體情況采用了非正交分解法,將桿對球的作用力沿斜面方向和沿桿方向分解,這種反常規的方法使問題迎刃而解。
方法三巧妙地將兩個力的矢量三角形疊加,非常直觀地得到桿對兩球作用力合力的大小和方向,從而得到兩球對桿的作用力是一恒力,這種新穎、獨到的方法使問題拔云見日。
以上三種方法都體現了學生思維的創新性,對所學的基本知識和方法并不是機械地接受,而是進行了加工和創新,根據實際情況來解決問題,這也正是我們教育要達到的目的。
21世紀呼喚創新人才,而創新人才的培養關鍵是教育。教育要與時俱進,新課程改革要求高中物理教學要改變過去一味強調知識傳承的傾向,要不斷探索適合學生的教學,拓展學生的思維,提高學生的創新能力。在我們平時的教學中,我們應利用好教學的素材,采取多種教學方式,調動學生學習物理的興趣與主動性,推陳出新,適時地去激發學生創新思維,培養學生的創新能力,為國家和社會培養創新型人才。

