基于模糊控制的智能驗電接地機器人機械臂運動控制研究
劉益軍,李正強,賴建防,呂偉宏
(1.廣東電網有限責任公司 佛山供電局,佛山 528000;2.寧波天弘電力器具有限公司,寧波 315700)
驗電接地是電力現場作業防止人員觸電的必要安全措施。傳統架空線路驗電接地作業方式存在較高風險:一是需要作業人員登高并人工驗電及裝設接地線,存在高空墜落和觸電風險;二是工器具設備沉重,接地線易纏繞身體,單純依靠人力執行耗時、耗力,效率低下[1-3]。如今使用機器人代替部分人工作業,降低人員風險成為解決方案之一,但為使驗電接地機器人準確完成驗電、接地工作,即對機械臂運動進行精確控制,需對機器人控制算法進行研究。
現有的機械臂運動可分為基于模型與不基于模型的方法。基于模型的方法有反演控制、自適應控制、滑模控制等,受限于系統數學建模的建立,多應用于動力學特性簡單的系統[4-8];不基于模型的控制方法有PID 控制、模糊控制等,解決控制中的誤差和干擾問題,但參數的選擇以經驗為主[9-11]。
智能驗電機器人機械手具有兩個關節,是一個多輸入、高度非線性、強耦合的系統,存在負載質量、連桿質心位置、動靜摩擦力等不確定參數,使傳統控制方法效率降低,難以得到準確數學模型[12-14]。綜上所述,綜合反演控制、自適應控制、模糊控制的特點,提出了基于自適應模糊反演控制算法,實現對智能驗電機器人機械手運動軌跡精確控制。
1 機械臂自適應模糊反演控制模型建立
為使智能驗電機器人機械臂運動滿足預設軌跡,即通過控制各關節輸出力矩,使機械臂位置、速度等變量滿足運動要求,需對機械手閉環運動控制算法進行研究,本文建立的閉環控制系統如圖1所示。
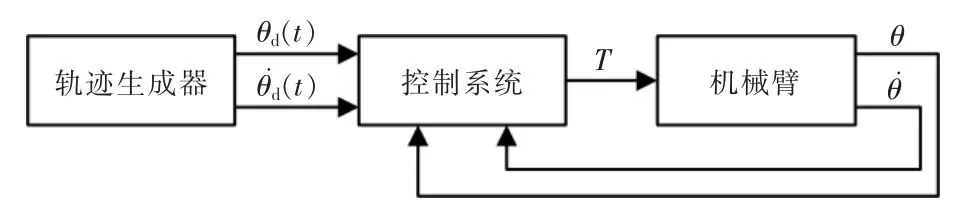
圖1 智能驗電機器人機械臂閉環運動控制系統框圖Fig.1 Block diagram of closed-loop motion control system of robot arm of intelligent electro-detector robot
結合模糊理論與自適應控制,設計適用于智能驗電機器人機械臂自適應模糊控制器,通過實時修正控制系統參數,使控制器適應變換的動態載荷,避免人的經驗獲得模糊控制規則的主觀性。智能驗電機器人兩自由度機械臂機構簡圖如圖2所示。
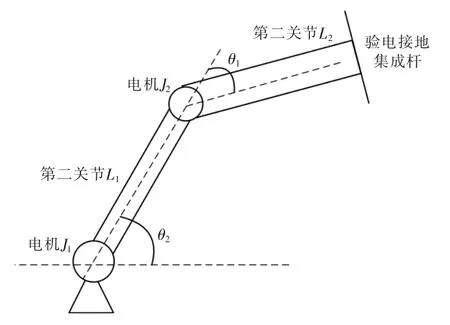
圖2 智能驗電接地機器人機械臂機構示意圖Fig.2 Schematic diagram of mechanical arm mechanism of intelligent electric grounding robot
對機械臂進行動力學分析,動態方程如下:
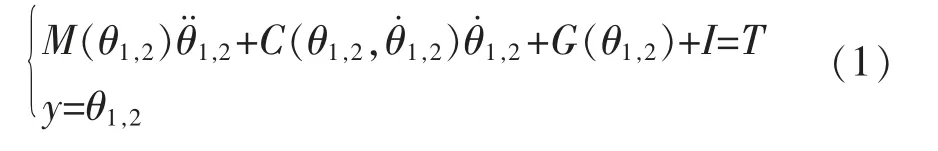
機械臂轉動慣量與向心力和科里奧利力關系如下:
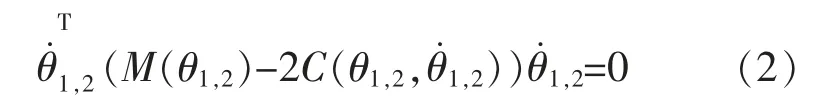
1.1 機械臂反演控制器設計
為便于反演控制器設計,設x1=θ,x2=,式(1)可表示為[17]
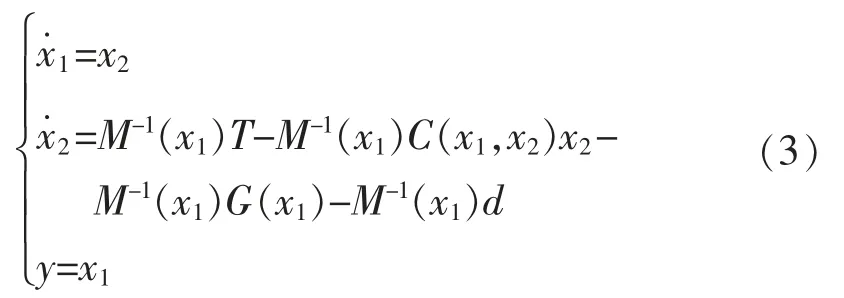
式中:d 為外界干擾項,反演控制器的控制目標為關節角度y,定義實際運動軌跡與理論軌跡角度誤差為

角速度誤差為


式中:λ1為機械臂第一關節控制系數;為估計量一
階導數。
針對機械手第一關節,取李亞普洛夫函數為
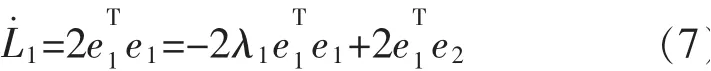
當e2=0 時,第一關節運動穩定。對于機械手第二關節,角速度誤差導數可表示為
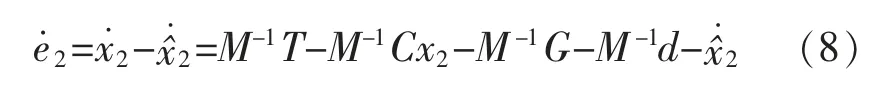
對于機械手整體,可取控制力矩為

式中:λ2為機械臂第二關節控制系數,φ 為角度誤差。
機械臂第二關節李亞普洛夫函數為
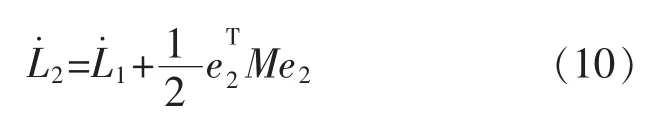
對式(10)求導,結合機械手整體控制律得:
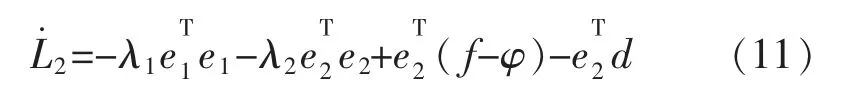
1.2 機械臂自適應模糊控制器設計
本文模糊系統部分由單值模糊化、中心平均反模糊化和乘積推理機模型構成。機械臂第一關節、第二關節轉動角度θ1,θ2和角速度為模糊系統輸入,定義模糊集:負(N),零(Z),正(P)。機械臂第一、二關節模糊系統為[18-19]
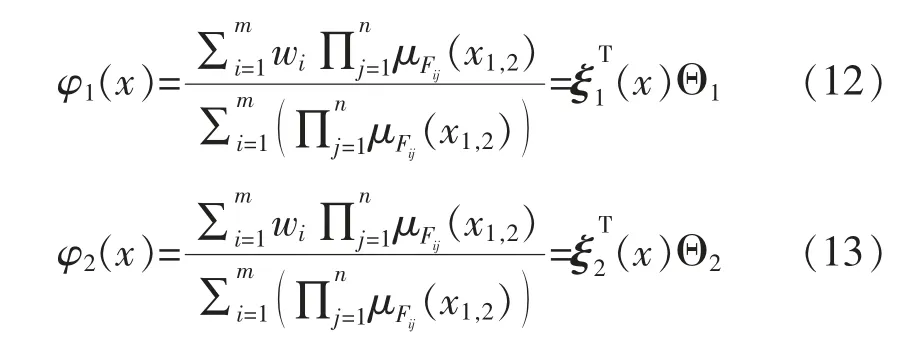
式中:w 為系統輸出;μF為高斯分布函數;ξ1T,ξ2T為模糊矢量。Θ1= [w1,w2,…,wm]T,Θ2= [w1,w2,…,wn]T,為系統輸出矢量。
2 仿真試驗
仿真試驗基于MATLA 工具箱Simulink 進行,通過對機械臂雙關節控制進行自適應反演模糊控制算法分析。為便于仿真,對機械臂進行坐標設定[20],結構如圖3所示。
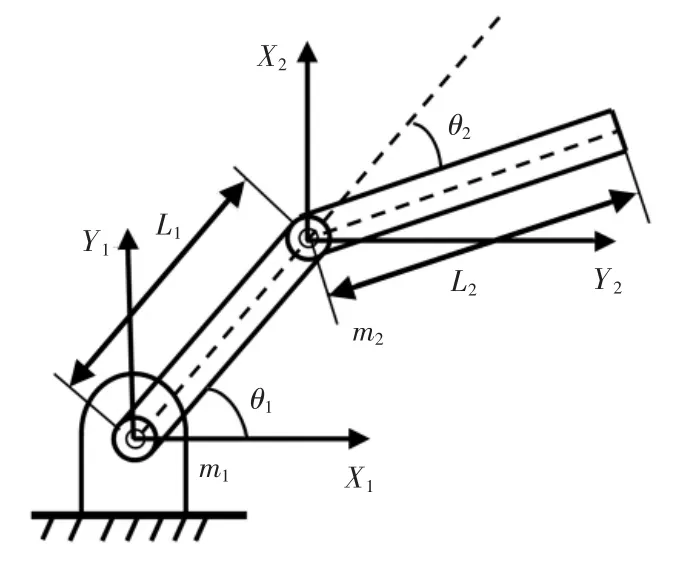
圖3 雙關節機械臂Fig.3 Double-joint robotic arm
圖3中L1,L2為兩連桿長度;m1,m2為兩連桿重量;θ1,θ2為連桿轉動角度。簡化后機械臂參數如表1所示。

表1 機械臂參數Tab.1 Manipulator parameter
根據連桿運動方式可將機械臂關節角度表示為

設機械臂初始狀態為x(0)=[1,0 ]T,關節期望軌跡為y=sin(2πt),模糊系統中采用高斯函數作為隸屬度函數:
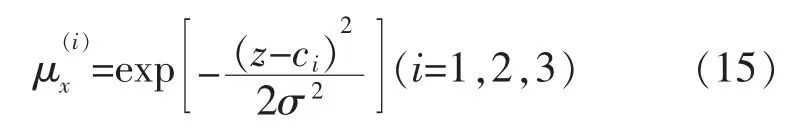
取函數均值ci分別為-1.25,0 和1.25;函數偏移量σ 為0.5。求得隸屬度函數如圖4所示。
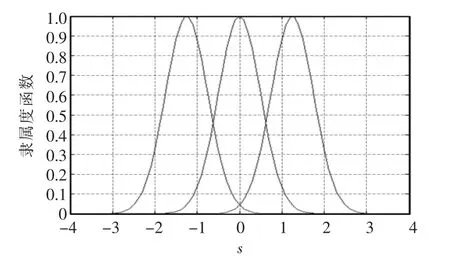
圖4 模糊隸屬度函數Fig.4 Fuzzy membership function
設自適應模糊反演算法中第一、二關節控制系數分別為:λ1=6,λ2=10。因實際控制中機械臂制造及安裝精度等外部因素影響,為減小控制算法仿真精度與實際精度誤差,設隨機干擾誤差d=[0.2sint,0.2cost],誤差采樣時間周期為0.01 s。則關節一、二位置軌跡跟蹤及跟蹤誤差仿真如圖5和圖6所示,其中跟蹤誤差為仿真軌跡與理論軌跡之差。
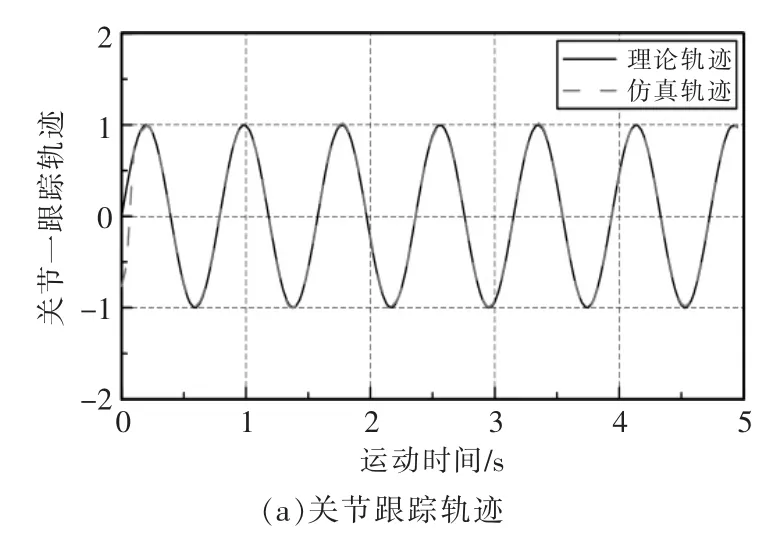

圖5 關節一定位分析Fig.5 Positioning analysis of joint 1
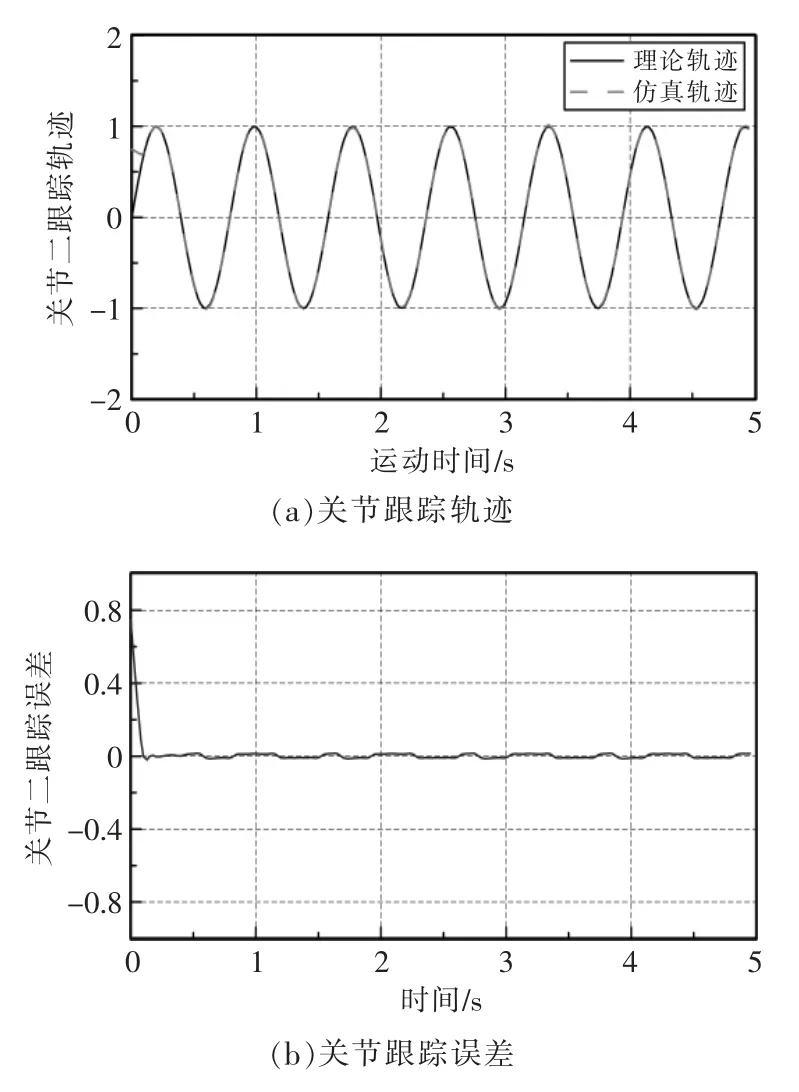
圖6 關節二定位分析Fig.6 Positioning analysis of joint 2
由圖5和圖6可知,自適應模糊反演算法對機械臂雙關節控制均具有較高跟蹤精度,其跟蹤誤差均小于0.80 rad,滿足工程需求。因存在響應時間,所以關節初始運動階段,跟蹤誤差較大,當運動達到穩態時,關節仿真跟蹤軌跡與理論軌跡誤差較小。穩態時關節一最大跟蹤誤差為0.0075 rad,響應時間為0.12 s,關節二最大跟蹤誤差為0.012 rad,響應時間為0.09 s。
綜上所述,自適應模糊反演控制算法對驗電接地機器人雙關節機械臂運動控制具有良好的適用性,解決了機械臂運動過程中的非線性及不確定性問題,較傳統的模糊控制算法,響應時間較短,跟蹤定位精度有顯著提高。
3 結語
本文提出自適應模糊反演算法應用于智能驗電機器人機械臂控制,解決了系統中參數不確定、高非線性、強耦合等問題。在自適應模糊反演算法下機械臂雙關節響應時間分別為0.12 s,0.09 s,穩態時最大跟蹤誤差分別為0.0075 rad,0.012 rad。自適應模糊反演算法對機械臂雙關節控制均具有較高跟蹤精度,其跟蹤誤差均小于0.80 rad,滿足跟蹤精度需求。
針對機器人機械臂運動控制難度高、技術復雜的難題,結合反演控制、自適應模糊控制理論,提出了自適應模糊反演控制算法,實現了智能驗電機器人機械臂運動軌跡閉環控制。完成了機械臂反演控制器、自適應模糊控制器設計,通過仿真實驗驗證了跟蹤控制的準確性和適用性,對機器人結構設計、工程應用具有重要指導意義。

