利用電磁場動量互易定理導出惠更斯原理*

劉國強 劉婧

1) (中國科學院電工研究所,北京 100190)

2) (中國科學院大學電子電氣與通信工程學院,北京 100049)

經典電磁場互易定理(即洛倫茲互易定理)作為電磁學重要的理論之一,被廣泛應用于通信、天線信號傳輸和電磁成像等諸多領域,它是一種“能量型”互易定理.已有研究用微分形式擴展“Rumsey 反應”的概念,使其同時包含了洛倫茲力密度反應和功率密度反應項.進一步有研究從麥克斯韋方程組導出了動量互易定理.動量互易定理與洛倫茲互易定理一樣,既可以用于理論分析,也可以解決實際應用問題.因此利用洛倫茲互易定理可導出惠更斯原理,本文利用動量互易定理導出惠更斯原理.

1 引言

1896 年,洛倫茲[1]提出的經典電磁互易定理是電磁學重要理論之一,它將兩個獨立的電磁場聯系起來,反映了兩組場源之間的能量相互作用.洛倫茲互易定理在電磁場理論分析和實際應用中發揮了重要作用,如可為論證波導元件和天線的互易性提供基礎[2],可用于確定波導和空腔諧振器中波型間的正交性[3],也常用于電磁成像等圖像重建問題的求解[4,5].

此后百余年間,人們陸續被發展了一些新的電磁互易定理,包括頻率域和時間域的互易定理,如Feld-Tai 互易定理[6,7]和互能定理[8,9]等.

上述定理均為“能量型”互易定理.事實上,電磁場除了具有能量還具有動量,因此從兩組場源的相互作用關系來看,除了能量作用關系,還應當有動量作用關系.2020 年,Lindell 等[10]采用微分形式對“Rumsey 反應”的概念進行了拓展,導出了時空統一形式的廣義反應密度.它對應的吉普斯矢量形式為

廣義反應密度同時包含了洛倫茲力密度反應和功率密度反應,其中洛倫茲力密度反應為空間項,功率密度反應為時間項,(1)式中 e4為時間基.

同年,Liu 等[11,12]從麥克斯韋方程組導出了兩組反映電磁場源之間動量相互作用關系的定理,分別為

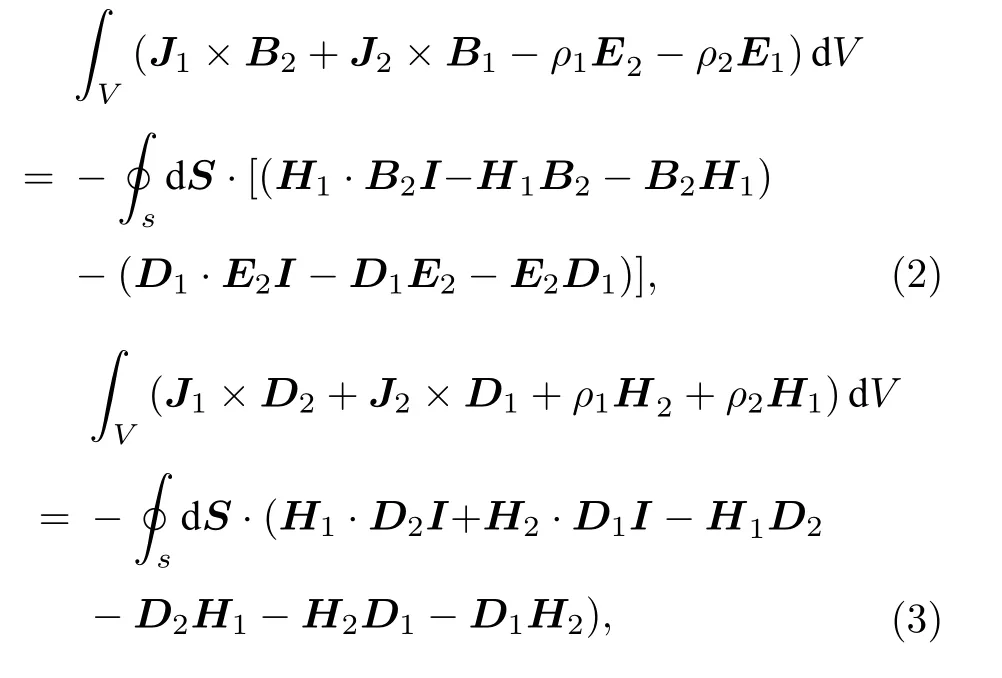
式中,I 為單位并矢,ρ,J,B,E,H 和 D 分別為電荷密度、電流密度、磁通密度、電場強度、磁場強度和電通密度,下角標1 和2 代表兩組電磁場.

這兩組動量互易定理是對洛倫茲互易定理和Feld-Tai 互易定理的擴展,與能量型互易定理一樣,可在工程實際應用中發揮重要作用,例如,在醫學磁聲電成像中利用動量互易定理進行圖像重建[12],亦可成為電磁場理論分析的重要工具,例如,通過動量互易定理導出惠更斯原理.

惠更斯原理是一個比較特殊的電磁原理,它深刻揭示了波的形成和波的本質.惠更斯原理是將波前上的每一點作為一個新的波源,根據這些源在波傳播方向上所產生場的疊加找出傳播規律.惠更斯原理提供了一種電磁場簡化分析方法,可以不用考慮實際源分布,只需在閉合面上設置與實際源等效的惠更斯源來簡化分析.前人用洛倫茲互易定理可以導出惠更斯原理[13],本文利用動量互易定理導出惠更斯原理,說明了一些經典電磁理論相互之間存在內在聯系.

2 理論模型

設實際電流源和磁流源分別為 Je1和 Jm1,電荷源和磁荷源分別為ρe1和ρm1.做閉合面Sh,該閉合面圍成的區域為Vh.

設P為Sh外 一點,在P點放 入IΔl的電 流元,可看作電流I分布在體積為 ΔV的小導體圓柱電流段V2,eP為圓柱上表面A的單位法向方向矢量,也是電流密度的方向.當圓柱體積趨于零時,電流段的電流密度為

式中δ(r-rP) 是三維δ函數,其量綱是 m-3.

電流段等效為圓柱V2的上表面A和下表面B分布等量異種面電荷的電偶極子.當IΔl為1 A·m時,該電流段即為單位電偶極子點源,可表示為

根據電流連續性定理可知,圓柱V2的上下表面滿足

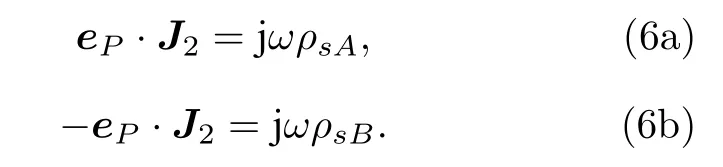
于是,圓柱V2的上下表面的面電荷為

式中ω為角頻率,矢徑 rP在圓柱的上下表面分別化為 rA和 rB.做一個包圍P點和Sh面的閉合面S,體積為V,如圖1 所示.

圖1 實際的電流源、磁流源、電荷源和磁荷源產生的場Fig.1.Fields generated by the actual current,magnetic current,charge sources and magnetic charge sources.

由于ρ2只分布在V2范圍,故ρ2E1在區域V中的積分等于它在區域V2中的積分,即

面電荷可看作載荷層厚度h趨于零而載荷體密度趨于無限時二者乘積的極限值,即有:

將(7)式和(9)式代入(8)式,有

在區域V中,應用動量互易定理,并利用δ函數性質,有

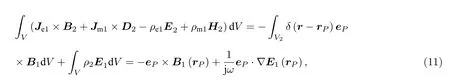
式中 E1(rP) 和 B1(rP) 分別為實際源產生的電場強度和磁通密度.

為確定Sh面上惠更斯源密度,將實際源拿走,在Sh面上放置等效的源 Jes,Jms,ρes和ρms,如圖2所示.

圖2 惠更斯面電流源、面磁流源、面電荷源和磁荷源產生的場Fig.2.Fields generated by the Huygens surface current,magnetic current,charge sources and magnetic charge sources.

等效的面流(或)源可看作載流層厚度h趨于零而載流(或荷)體密度趨于無限時二者乘積的極限值,即有

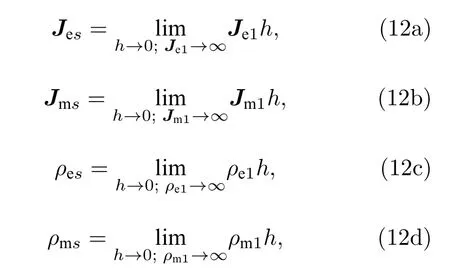
在區域V中,有

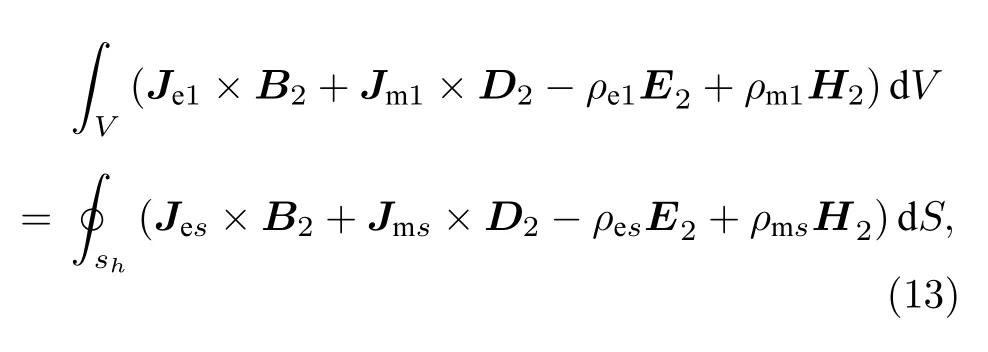
應用動量互易定理,有

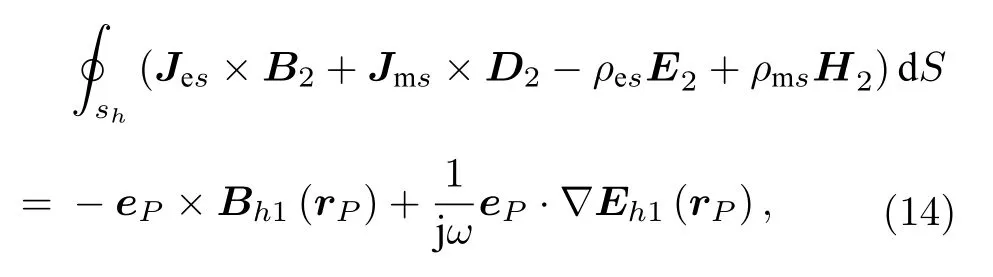
式中 Eh1(rP) 和 Bh1(rP) 是惠更斯面上的等效源產生的電場強度和磁通密度.

由于 Jes,Jms,ρes和ρms是實際源的等效源,必有

考慮到 eP方向的任意性,有

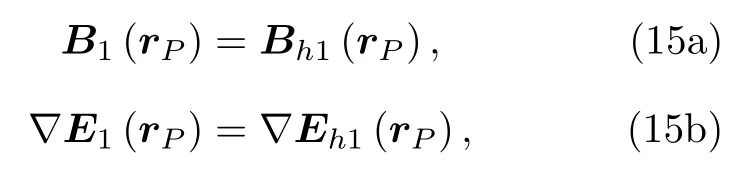
在Vh區域使用動量互易定理,有

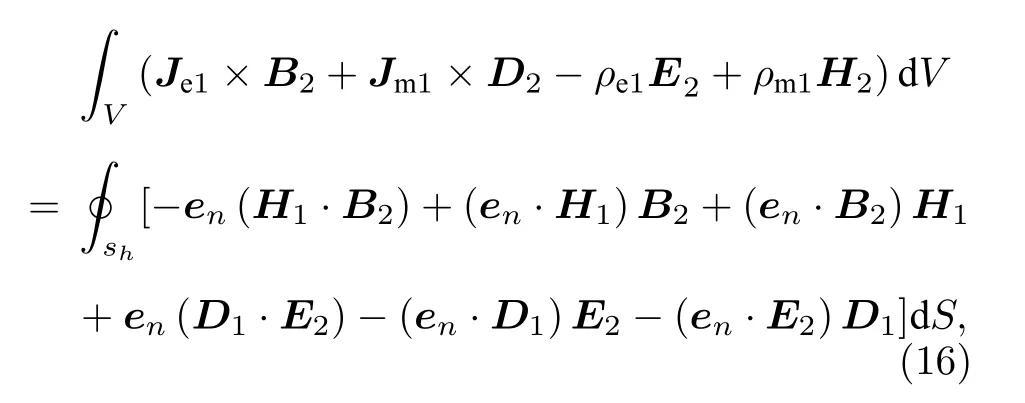
(11)式和(16)式的體積分相等,有

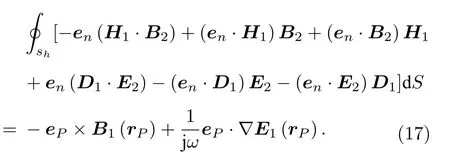
利用(15)式,可知(14)式和(17)式的面積分相等,即

利用恒等式

有

將(19)式代入(18)式有

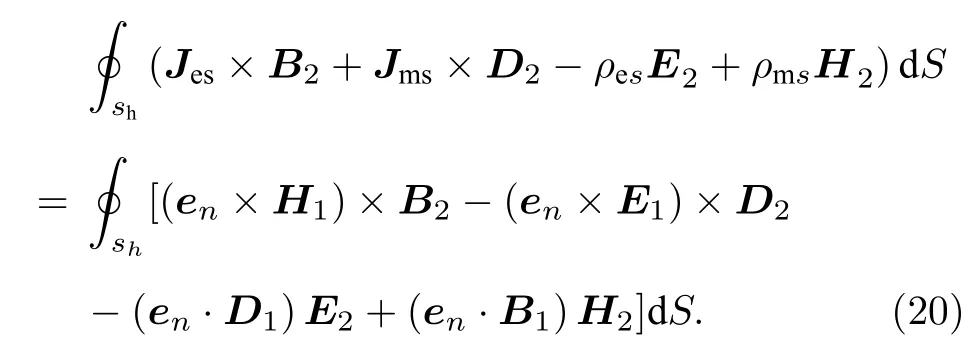
比較 (20)式兩端,可知惠更斯源密度為

(21)式和(15)式表示,對惠更斯面Sh外的場點P,要產生相同的磁通密度,Sh面上應放置惠更斯面電流源 Jes、面磁流源 Jms、面電荷源ρes和面磁荷源ρms.對比洛倫茲互易定理導出的等效源,動量互易定理導出的等效源增加了面電荷源ρes和面磁荷源ρms,但在惠更斯面上,流源與荷源之間并非獨立,Jes和ρes以及 Jms和ρms分別可以通過電流連續性定理和磁流連續性定理聯系起來.

同理,若在點P放置單位磁偶極子,亦可以導出(21)式,類似于(15)式,可以導出:

聯合(21)式和(22)式可知,對惠更斯面Sh外的場點P,要產生相同的電通密度,Sh面上應放置惠更斯面電流源 Jes、面磁流源 Jms、面電荷ρes和面磁荷ρms.

3 結論

本文利用動量互易定理導出了惠更斯原理,豐富了電磁場基礎理論,為惠更斯原理及其應用提供了新的研究思路.