空隙率對丁壩周圍水位影響數值模擬研究*

喻 濤，段秋鉛，王平義，蘆 冉，劉倩穎

(1.重慶交通大學，水利水運工程教育部重點實驗室，重慶400074；2.重慶交通大學，國家內河航道整治工程技術研究中心，重慶400074；3.重慶市水文監測總站，重慶400014)

丁壩作為航道整治中最常用的一種阻水建筑物，具有束窄水流、壅高水位、改變原有河道局部水流流態和水沙條件的作用。Mostafa等[1]通過動床試驗對比分析透水丁壩與實體丁壩對主航道水深影響，認為透水丁壩主航道中心線處水深不會改變，實體丁壩主航道中心線處水深會發生一定改變；李明龍等[2]通過水槽概化試驗研究壩體挑角、流量以及不同壩頭形式對雙丁壩周圍水面線的影響，得到上、下丁壩壩頭均為圓弧直頭時水面橫縱比降最大的結論；劉煥芳等[3]通過模型試驗推導出樁柱式透水丁壩壅水高度經驗公式，認為丁壩壅水高度主要與壩長、河道水深以及透水率有關；許百強等[4]通過水槽概化模型試驗研究不同空隙率和空隙尺寸對透水丁壩周圍橫縱斷面水面線的影響規律，認為在一定的空隙率和空隙尺寸條件下，透水丁壩對其上游的壅水效果更佳；在此基礎上，贠寶革等[5]研究不同空隙尺寸和不同空隙率對壩身段、壩頭前端和主流帶區能量變化的影響，得到在壩身段空隙尺寸越小，水流通過損耗的位能就越小的結論；閆杰超等[6]研究淹沒齒型丁壩阻力與淹沒程度之間的關系，認為淹沒度與阻力系數呈反比關系；Ahmed等[7]研究丁壩相對長度對其周圍水流結構、流速和水深的影響；Yu等[8]通過水槽試驗，研究丁壩周圍紊動與局部沖刷之間的關系；常留紅等[9]通過水槽試驗研究透水率指標對空心梯形塊丁壩透水特性的影響規律；楊元平[10]推導出透水丁壩壩后回流區長度計算公式，認為透水丁壩壩后回流區長度與壩長、壩邊坡、水深以及丁壩透水性有關；任志等[11]通過動床模型水槽試驗研究水力插板式透水丁壩的性能，并認為當透水率為30%時，水力插板透水丁壩的防沖促淤效果達到最佳。事實上，天然河道中的丁壩三維水流情況非常復雜，計算機技術的飛速發展為復雜水流問題的計算提供了計算手段，黃文典等[12]通過研究認為將有限元方法 、Newton-Raphson 迭代法與平面二維數學模型結合的計算方法用于淹沒丁壩條件下的水流數值模擬是可行的；Duan等[13]利用改進二維模型對天然河道中泥沙輸運過程進行仿真試驗；劉玉玲等[14]應用高精度的加權基本無震蕩格式(weighted essentially non-oscillatory schemes，WENO)結合有限體積法建立河道丁壩群二維水流的數學模型，并驗證該模型能夠有效地計算復雜邊界天然河道丁壩群二維水流水力特性問題。近年來越來越多的學者開始進行丁壩的三維數值模擬，如李志勤等[15]采用控制體積法和標準的k-ε(湍流動能-耗散率)模型相耦合的方法驗證了流體體積(volume of fluid，VOF)模型對模擬丁壩影響范圍內自由水面的可行性；Ouillon 等[16]利用三維k-ε模型研究丁壩周圍三維水流結構和自由液面形狀，并求解壩后沖刷區水流的水力特性；楊蘭等[17]采用 FLOW-3D 軟件，對上挑丁壩群的周圍流場分布和局部沖刷進行三維數值模擬，并得出可適用于計算丁壩群的湍流模型和推移質輸沙率模型；郭延祥等[18]利用FLUENT軟件對淹沒式丁壩周圍流場進行了數值模擬研究，得到丁壩主流區的流速較大而回流區的流速較小的結論；王文森等[19]通過粒子圖像測速技術(PIV)試驗和FLOW-3D 數值模擬相結合的方法研究均勻開孔的梯形透水潛壩附近水面線與壩體透水率的關系，認為潛壩結構附近水面線壅水及水跌高度隨著透空率逐漸增大而減小，并得到透水率綜合公式。

以上學者通過物理模型試驗和數學模型等方法對丁壩周圍水力特性進行研究，試驗的丁壩形式越來越多，但對梯形橫斷面圓弧頭形式的透水丁壩的研究甚少。本文基于FLOW-3D計算流體力學軟件建立透水丁壩水動力特性數值模型，考慮丁壩剛好淹沒情況，開展空隙率對丁壩壩身段、壩頭段以及主流帶區各個位置水位變化影響研究，研究結果對合理選取透水丁壩空隙率具有一定參考價值。

1 基本理論

本文將流體視為不可壓縮黏性流體，即：

(1)

流體的動量守恒定律由Navier-Stoke方程描述，即：

(2)

(3)

(4)

式中：Ax、Ay、Az分別為流體在x、y、z方向單元面內流體可流過區域的面積分數；u、v、w分別為x、y、z方向上的速度分量(m/s)；VF為單元內流體可流動區域的體積分數；ρ為流體密度(kg/m3)；Gx、Gy、Gz分別為流體在x、y、z方向上的質量力加速度(m/s2)；fx、fy、fz分別為流體x、y、z方向上的黏滯力加速度(m/s2)；p為作用在流體微元上的壓力(N/m2)。

FLOW-3D中有以下紊流模型可以采用：普朗特混合長度模型、一方程模型、兩方程k-ε模型、重整化群(renormalization group，RNG)k-ε模型以及大渦模型。RNGk-ε模型可以更準確地描述低強度湍流和強剪切區域的流動，故本文采用RNGk-ε紊流模型模擬計算。

2 模型設計及驗證

2.1 模型設計

2.1.1數學模型水槽設計

采用FLOW-3D軟件模擬矩形水槽中透水丁壩周圍水動力場，矩形水槽長30.0 m、寬2.0 m、高0.2 m。通過對長江上游丁壩尺寸的總體統計研究，并結合實際試驗條件，采用1:40的正挑丁壩作為模型丁壩，該丁壩采用梯形橫斷面圓弧頭丁壩，壩長50 cm、高10 cm，壩頂、底寬分別為7.5、42.5 cm。模型丁壩的迎水坡坡比1:1.5，背水坡坡比1:2.0，向河坡坡比1:2.5。透水丁壩為圓形空隙，空隙半徑為16 mm，設計7個空隙率：P1=6.4%、P2=10.3%、P3=12.8%、P4=15.4%、P5=18.0%、P6=20.6%、P7=23.2%；實體丁壩空隙率為P0=0%；控制流量Q=65 L/s，控制(壩前)水位H=11 cm，試驗工況見表1。

表1 試驗工況

2.1.2物理模型水槽設計

為了對數學模型水槽進行率定，另在實驗室內進行與數學模型水槽尺度一樣的物理模型水槽試驗，分別布置了9個橫斷面和9個縱斷面，并測量各斷面水位，模型布置見圖1。

2.2 網格劃分與邊界條件

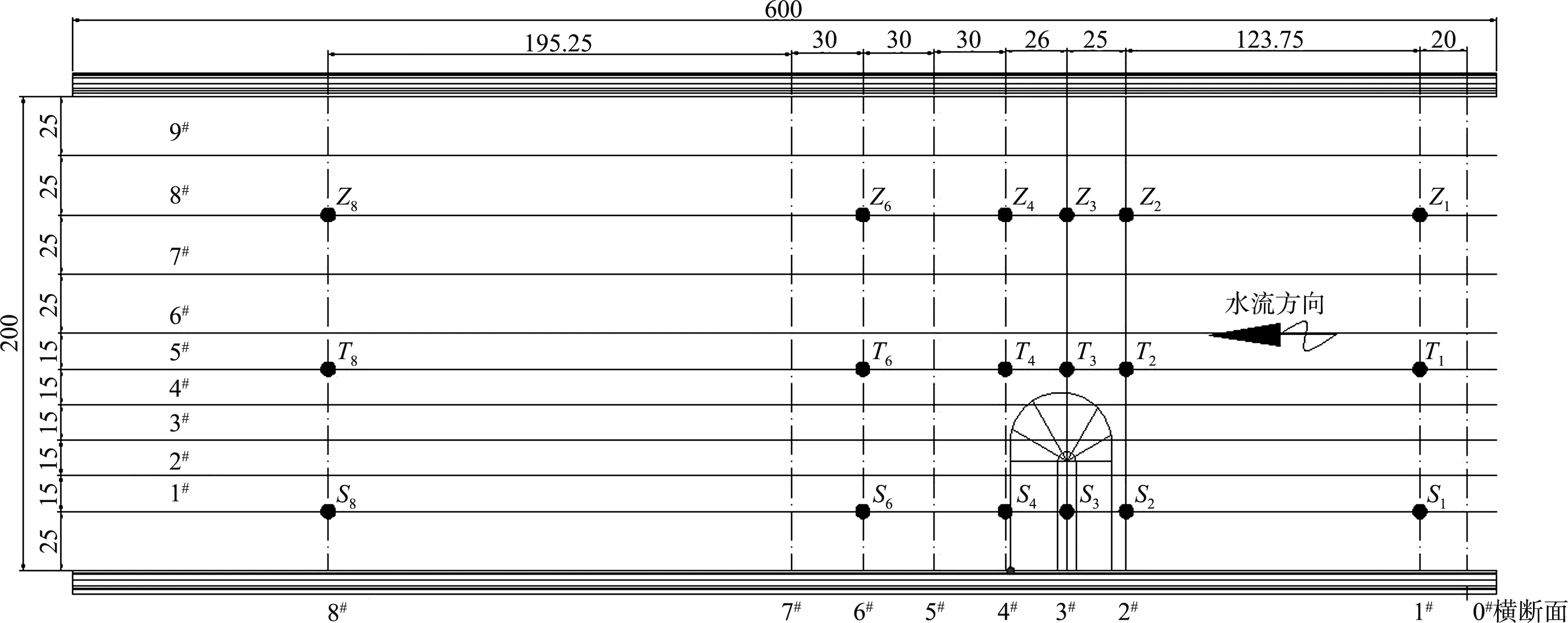
圖1 物理模型水槽布置(單位：cm)

透水丁壩模型見圖2，數值模擬范圍為丁壩上游15 m—下游15 m，采用正六面體結構化網格，x、y、z方向網格尺寸為2 cm。xmax方向采用流量邊界，入口流量為65 L/s，對應水位為11 cm；xmin方向為壓力邊界，設置出口水位10 cm；zmax方向同樣設置為壓力邊界，賦予大氣壓；其余邊界均采用無滑移壁面WALL條件。

圖2 R=16 mm、P=15.4%透水丁壩三維模型

2.3 模型驗證

以物理模型試驗結果對比數值模擬結果進行驗證，選取壩前2#斷面、壩后4#斷面，以及P=0%，R=0 mm，Q=65 L/s、H=11 cm工況進行模型水位驗證，結果對比見圖3。可以看出，數模計算結果與物模實測結果的最大偏差為0.2 cm，平均偏差為0.1 cm，說明數值模擬能較好地模擬透水丁壩周圍水動力情況，其具有較好的可靠性。

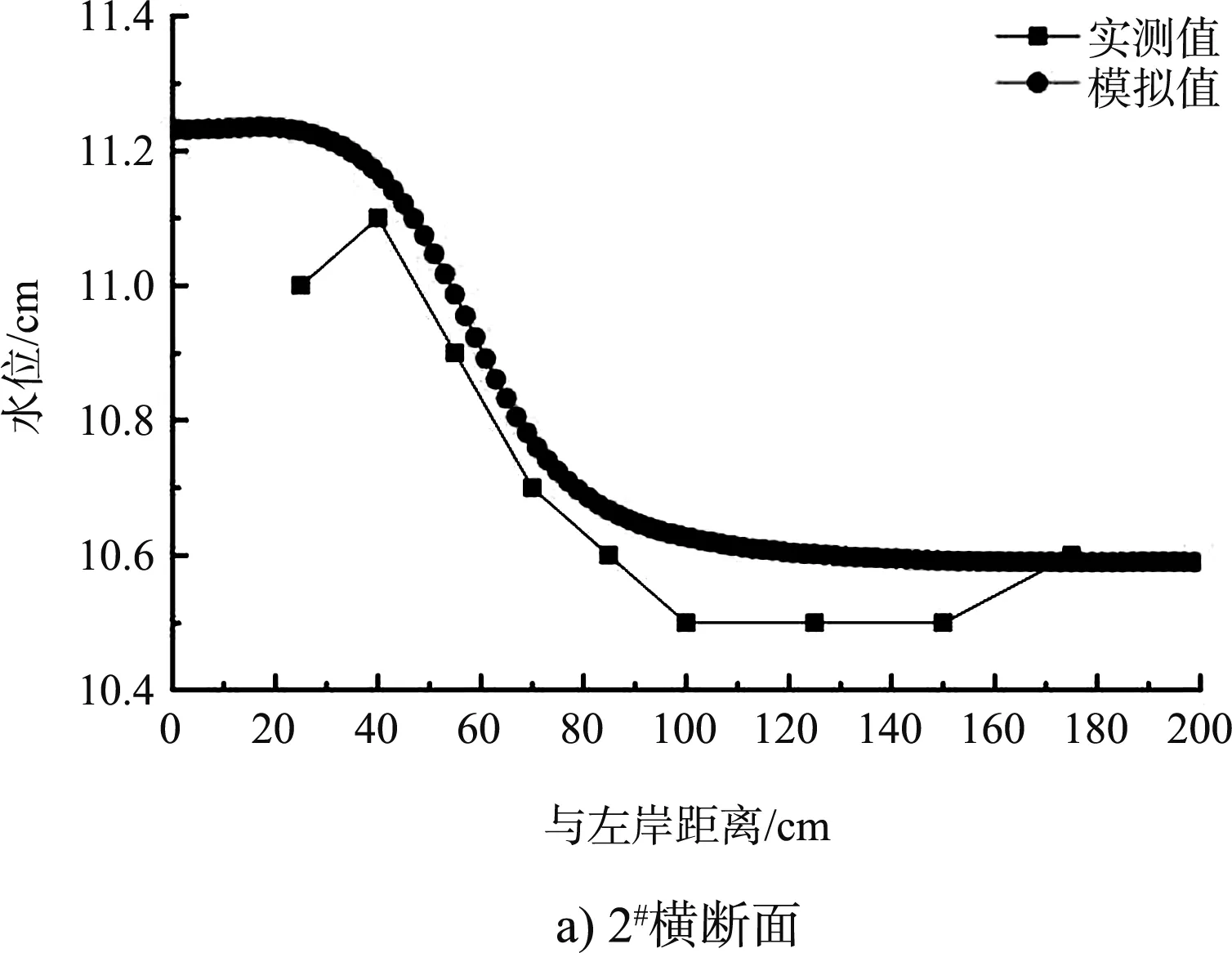
圖3 數模計算與物模實測水位驗證

3 試驗結果

3.1 壩身段各位置水位變化分析

將試驗區劃分為壩身段、壩頭前端和主流帶區，其中壩身段為1#、2#縱斷面，壩頭前端為5#、6#縱斷面，主流帶區為8#、9#縱斷面，選取壩前1#、2#、壩軸線3#、壩后4#、6#以及遠離壩體8#橫斷面與1#、5#、8#縱斷面的交點(圖1)進行水位分析。

選取1#縱斷面分析壩身段各個位置水位與空隙率之間的關系，其各個位置水位隨空隙率變化關系見圖4。

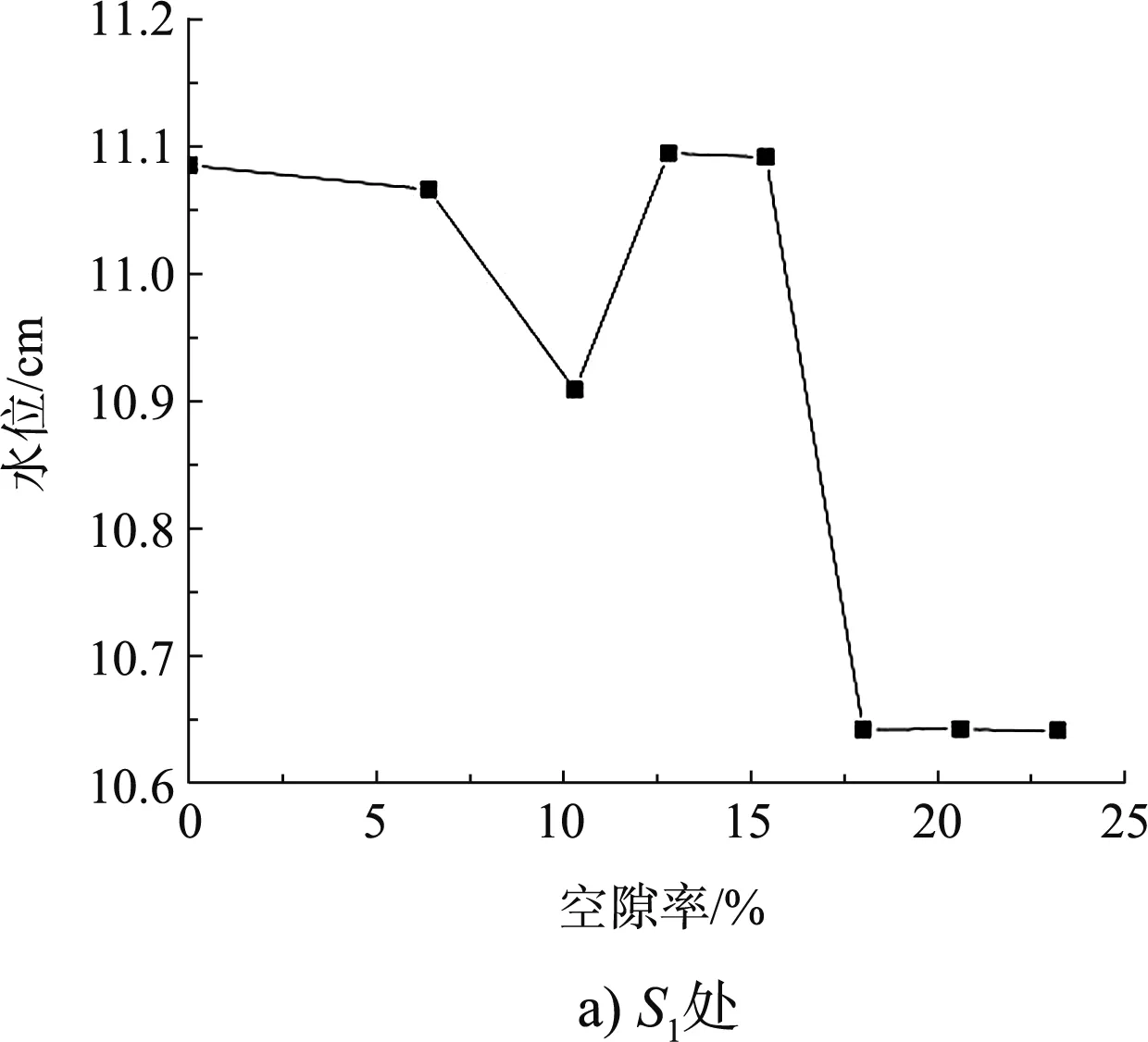
圖4 1#縱斷面不同空隙率條件下壩身段水位變化

由圖4可知，壩身段(1#縱斷面)，S1、S2處，水位隨著空隙率的增大變化趨勢大體一致，在空隙率小于15.4%時，隨著空隙率增大，水位先降低后升高；在S3處，當空隙率大于15.4%時，水位減小至10.64 cm后趨于穩定，水位隨著空隙率增大呈現上下波動，在空隙率為20.6%時，水位迅速下降，此時S3位置剛好是空隙處，水流順著空隙流過丁壩，造成水位偏低。S4、S6處，隨著空隙率增大，水位總體呈現上升趨勢，但空隙率為12.8%時水位偏低。當空隙率小于15.4%時，S8處的水位隨著空隙率增大先升高后降低，當空隙率大于15.4%時，水位升高至10.26 cm后趨于穩定。

在壩身段，壩體上游區水位壅高與空隙率的關系表現為：中空隙率(12.8%、15.4%)時效果與實體丁壩基本一致，大空隙率(18.0%、20.6%、23.2%)時效果遠不如實體丁壩，小空隙率6.4%時效果與實體丁壩基本一致，空隙率10.3%時效果不如實體丁壩。壩體下游區水位與空隙率的關系表現為：各透水丁壩對抬高壩后水位均具有積極作用，大空隙率(18.0%、20.6%、23.2%)效果最佳，小空隙率(6.4%、10.3%)次之，中空隙率(12.8%、15.4%)效果稍差，該現象與文獻[4]的物理模型試驗結果一致，表明透水丁壩對水流的阻力與空隙率呈非線性關系；文獻[20]指出樹冠阻力系數與空隙率滿足一個近似二次多項式關系，即阻力系數隨空隙率增大先增大后減小，因此透水丁壩壩后水位出現這種現象是合理的。

3.2 壩頭前端各位置水位變化分析

選取5#縱斷面分析壩頭前端各個位置水位與空隙率之間的關系，其各個位置水位隨空隙率變化關系見圖5。

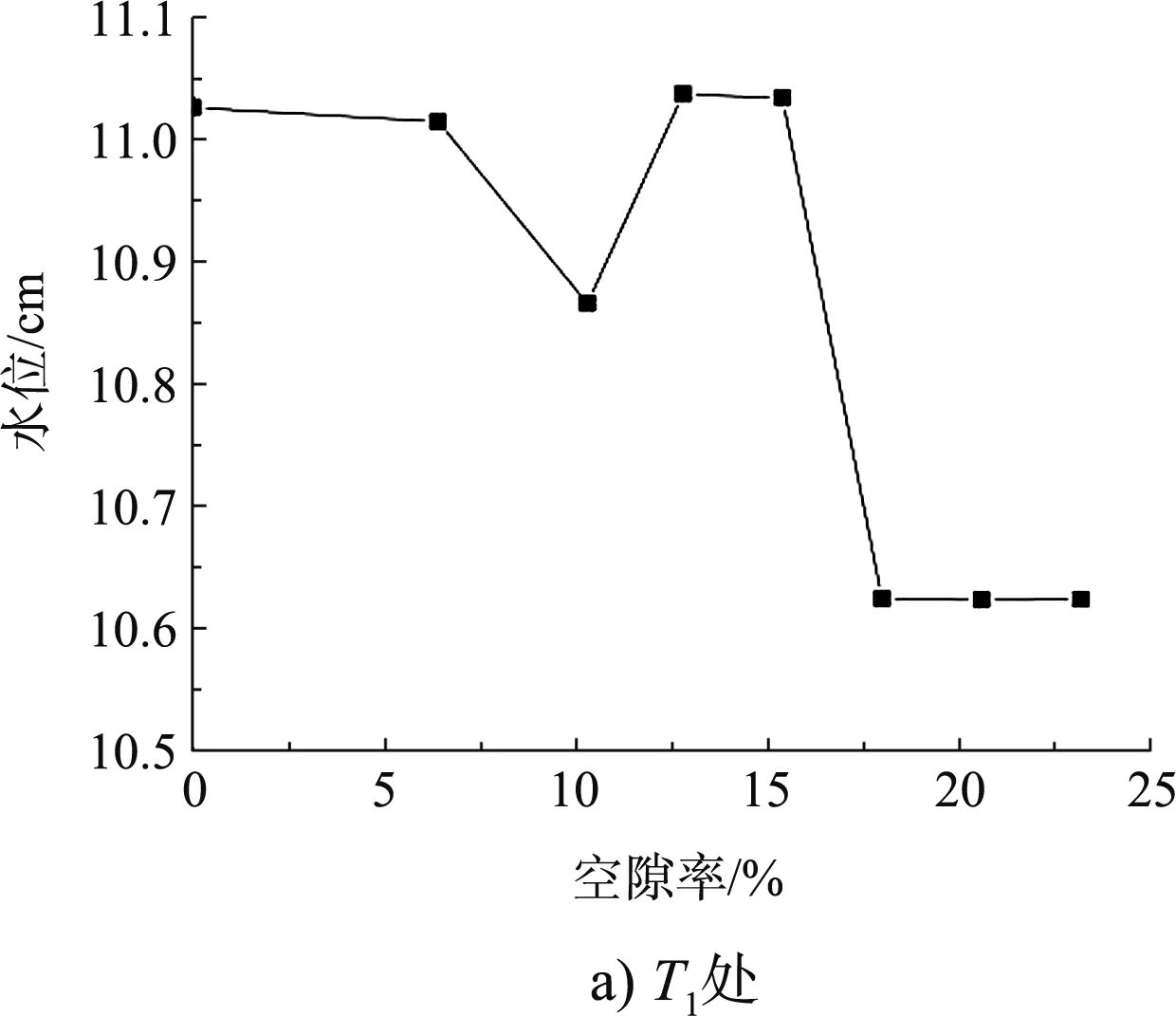
圖5 不同空隙率條件下壩頭前端水位變化

由圖5可知，壩頭前端(5#縱斷面)，在T1處的水位隨空隙率變化趨勢與S1處一致；在T2處，隨著空隙率增大，水位整體呈現上下波動，但水位變化趨勢不大，最大水位與最小水位僅相差0.18 cm；在T3處，當空隙率小于12.8%時，水位隨著空隙率增大先升高后降低，當空隙率大于12.8%時，水位升高至10.32 cm后趨于穩定。在壩體下游區(T4、T6及T8處)，水位與空隙率之間的變化關系與壩身段S4、S6及S8處基本一致。

在壩頭前端，壩體上游區水位壅高與空隙率的關系表現為：中空隙率(12.8%、15.4%)時效果優于實體丁壩，大空隙率(18.0%、20.6%、23.2%)時效果不如實體丁壩，小空隙率(6.4%、10.3%)時效果與實體丁壩基本一致。壩頭前端下游區水位隨空隙率的變化關系與壩身段下游區基本一致。

3.3 主流帶區各位置水位變化分析

選取8#縱斷面分析主流帶區各個位置水位與空隙率之間的關系，其各個位置水位隨空隙率變化關系見圖6。

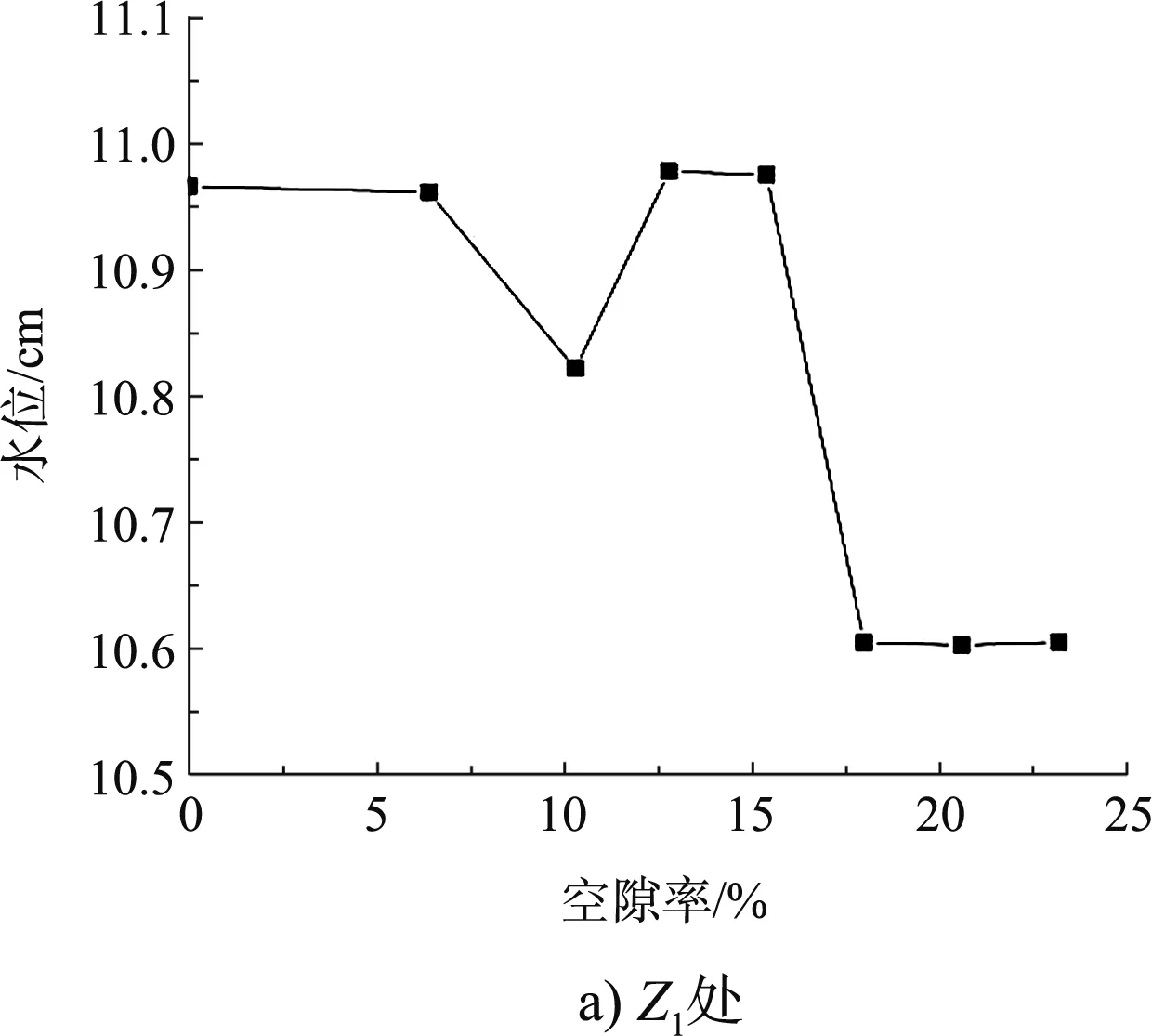
圖6 不同空隙率條件下主流帶區水位變化

由圖6可知，主流帶區(8#縱斷面)，在Z1處，水位隨空隙率變化趨勢與S1、T1處一致；在Z2處，隨著空隙率增大，水位呈現上下波動的變化趨勢，空隙率為10.3%時水位出現最小值；在Z3處，隨空隙率增大，水位上下波動，但整體變化很小，最大水位與最小水位相差僅0.058 cm。在壩體下游區(Z4、Z6及Z8處)，水位與空隙率之間的變化關系與壩身段S4、S6及S8處基本一致。

在主流帶區，壩體上游區水位壅高與空隙率的關系表現為：中空隙率(12.8%、15.4%)時效果與實體丁壩基本一致，大空隙率(18.0%、20.6%、23.2%)時效果不如實體丁壩，小空隙率6.4%時效果優于實體丁壩，孔隙率10.3%時效果不如實體丁壩。主流帶區壩體下游段水位與空隙率的變化關系與壩身段下游區基本一致。

4 結論

1)壩身段S1、S2處，當空隙率小于15.4%時，隨空隙率增大水位先降低后升高；當空隙率大于15.4%時，水位降低至10.64 cm后趨于穩定；在Z3處，水位隨著空隙率增大呈現上下波動，且波動較大；S4、S6及S8處，隨空隙率增大水位總體呈上升趨勢。

2)壩頭前端T1處，當空隙率小于15.4%時，水位隨著空隙率增大先降低后升高；當空隙率大于15.4%時，水位減小至10.62 cm后趨于穩定；在T2處，隨著空隙率增大，水位整體呈現上下波動，但水位變化趨勢不大，最大水位與最小水位僅相差0.18 cm；在T3、T4及T6處，當空隙率小于12.8%時，水位隨著空隙率增大先升高后降低，當空隙率大于12.8%時，水位升高至10.32 cm后趨于穩定；在T8處，水位在空隙率為15.4%時出現最低值。

3)主流帶區Z1處，當空隙率小于15.4%時，隨著空隙率增大，水位先降低后升高；當空隙率大于15.4%時，水位減小至10.60 cm后趨于穩定。在Z2、Z3處，隨空隙率增大，水位上下波動，但整體變化較小。在Z4、Z6及Z8處，當空隙率小于12.8%時，水位隨著空隙率增大先升高后降低，當空隙率大于12.8%時，水位升高至某一值后趨于穩定。

4)綜上所述，壩體上游區水位壅高與空隙率的關系表現為：中空隙率(12.8%、15.4%)時效果與實體丁壩基本一致，大空隙率(18.0%、20.6%、23.2%)時效果遠不如實體丁壩，小空隙率6.4%時效果與實體丁壩基本一致，空隙率10.3%時效果不如實體丁壩。壩體下游區水位與空隙率的關系表現為：大空隙率(18.0%、20.6%、23.2%)抬高壩后下游區水位效果最佳，小空隙率(6.4%、10.3%)次之，中空隙率(12.8%、15.4%)效果稍差，該現象與物理模型試驗結果一致，表明透水丁壩對水流的阻力與空隙率之間可能存在非線性關系，下一步將深入探究壩體阻力系數與空隙率之間的關系。