基于MMOAFSA蒸汽壓縮式制冷機組的雙參數前饋解耦PID控制策略研究

陰志杰 李紹勇 李東升 楊 睿

（蘭州理工大學土木工程學院 蘭州 730050）

0 引言

蒸汽壓縮式制冷機組（Vapor Compression Refrigerating Unit,VCRU）一般由壓縮機、冷凝器、熱力或電子膨脹閥和蒸發器構成，其中蒸發器在制冷循環中發揮著關鍵作用，即將低溫低壓的液態制冷劑進行氣化，釋放制冷量給空調冷凍水，從而對夏季的空調房間進行降溫[1]，滿足室溫Tn等于其設定值Tn,set的空調設計需求。蒸發器的熱工性能可通過兩個重要參數－蒸發溫度Te和過熱度Dsh來表征，而Te和Dsh測量值是否滿足制冷工藝所要求的相應設定值Te,set和Dsh,set，對于實際運行中的蒸發器和VCRU 具有重要意義[2]。因此，對Te和Dsh施加恰當的控制方式，確保Te≈Te,set和Dsh≈Dsh,set，可滿足蒸發器及其VCRU 的安全、穩定與節能運行需求。

從控制角度來看，關聯Te和Dsh的蒸發器這個被控對象具有結構參數時變、慣性大和時延等特性，采用傳統PID 控制策略，往往導致Te和Dsh的穩態誤差和超調量較大、調節時間較長等問題[3]，會影響蒸發器運行的穩定性。同時，Te和Dsh的控制回路之間還存在耦合效應，該耦合效應會使得Te=Te,set和Dsh=Dsh,set的預期控制效果下降。此外，蒸發器這個被控對象還存在較大的時滯τ，該時滯會使得Te和Dsh的控制系統穩定性下降。這些均導致蒸發器及其VCRU 運行性能降低和Te和Dsh動態響應變差[4]。因此，Te和Dsh控制問題及其VCRU運行模式的研究，成為當前空調與制冷裝置自動化領域的一個研究熱點。

針對復雜非線性的雙輸入雙輸出的VCRU，尚羽佳等[5]將無模型控制方法應用其節能控制方案中。仿真結果表明，過熱度和蒸發溫度的控制效果穩定，且動態響應得到了改善。張騰飛等[6]將PID控制器與改進型Smith 預估器相結合，實現了制冷系統中過熱度與蒸發溫度的雙回路Smith預估解耦PID 控制。設計擾動觀測器對系統的集中擾動進行估計并進行前饋補償。結果表明，該系統的抗干擾能力和跟蹤性能均得到了提升。文獻[7]采用自適應PID 控制器來控制冷凝器與蒸發器之間的電子膨脹閥開度OEEV。這樣PID 控制器的3 個參數（KP,KI,KD）是連續整定的，可適應室溫被控對象的結構參數變化。既動態改變OEEV和調控進入蒸發器的液態制冷劑流量qr，又滿足快速調節室溫Tn需求。

PID 控制方式由于其結構簡單、魯棒性強和可靠性高等特點因而在工業過程參數的控制中得到了廣泛的應用。其控制效果主要取決于相應PID 控制器參數的整定[8]，所以不少學者關注PID 控制器參數的整定算法研究。為了對光電伺服系統中的光束進行高精度，穩定的跟蹤，肖冰冰等[9]引入一種改進的螢火蟲算法（Improved Firefly Algorithm,IFA）對PID 控制器的參數進行優化整定。結果表明：對于該光電伺服系統（Photoelectric Servo System,PSS）相比Z?N 法，改進的螢火蟲算法對PID 控制器參數進行優化整定后，光束控制系統的響應速度、帶寬和跟蹤精度分別提高了40%，33.3%和25%。Chen 等[10]采用粒子群優化算法（Particle Swarm Optimiz-ation Algorithm,PSOA）對電機伺服驅動系統（Motor Servo System,MSS）的PID 控制器參數進行整定，結果表明該控制方法使得系統的動態性能和穩態性能得到了顯著的提高，其超調量、響應速度和ITAE 都有著顯著改善。

然而，衡量PID 控制系統質量的指標，如穩定性、快速性以及準確性等是一個相互制約的關系，同時滿足這些指標很困難[11]。Gilberto 等[12]將多目標優化方法應用于制冷壓縮過程中的Te與Dsh控制問題。將評價指標：積分絕對誤差（Integral Absolute Error,IAE）、控制量的總變化量（Total Variation,TV）和閉環對數模量（Closed loop Log Modulus,LCM）作為Te和Dsh的PID 控制器參數整定算法的目標函數，實現了對6 個控制器參數連續、多目標優化的整定，并取得了預期的Te和Dsh控制效果。文獻[13]采用改進多目標粒子群算法，以軌跡跟蹤偏差（Trajectory Tracking Error,TTE）和控制器輸出力矩（Controller Output Torque,COT）作為目標函數，對機器人軌跡跟蹤模糊PID 控制器中的162個參數進行優化整定。仿真結果表明了該方法對機器人軌跡跟蹤控制的有效性和優越性。

綜上，考慮密切Te和Dsh的蒸發器這個被控對象具有結構參數時變、慣性大和時延等特性及其Te和Dsh的控制回路之間存在耦合效應，為進一步提高Te和Dsh控制質量，本文提出蒸發溫度與過熱度前饋解耦PID 控制策略的設計理念，即VCRU雙參數前饋解耦PID 控制系統（Two-Parameter Feed-forward Decoupled PID Control System for VCRU?TPFDPIDCS），構建前饋解耦補償器的傳遞函數矩陣，消除這兩個控制回路之間的耦合效應。同時，對于Te和Dsh的PID 控制器參數整定問題，依據基本型單目標人工魚群算法，對人工魚的視野V和步長S進行指數遞減變化，構建MSOAFSA。再將多目標優化的混沌局部搜索策略引入MSOAFSA，得到MMOAFSA。以min(ITAE,tc,Ess)作為它的3 個目標適應度函數，設計出Te和Dsh的PID 控制器參數整定算法MMOAFSA，來獲取相應的參數最佳值和3 個目標函數的Pareto 最優解。仿真結果表明，該MMOAFSA 是可行的，能求解出兩個PID 控制器參數的最佳值和ITAE、tc和Ess的Pareto 最優解。同時本文提出的VCRU?TPFDPIDCS 可消除兩個控制回路之間耦合效應，Te和Dsh的調節品質得到明顯提升。

1 VCRU 的蒸發溫度與過熱度控制

1.1 單級制冷循環工藝

如上所述，VCRU 包括壓縮機、冷凝器、熱力或電子膨脹閥和蒸發器。蒸發器發揮著將低溫低壓的液態制冷劑進行氣化，釋放制冷量給空調冷凍水的作用，實現對夏季的空調房間進行降溫，滿足室溫Tn≈Tn,set的空調設計需求。采用電子膨脹閥的VCRU 單級制冷循環工藝[2]，相應的測控流程圖如圖1所示。

分析圖1：由蒸發器排出的低溫低壓制冷劑蒸汽被壓縮機吸入，再經過壓縮機的做功，使其變成高溫高壓的制冷劑蒸汽后排入冷凝器。在冷凝器中與空調冷卻循環水進行熱量交換，而被冷凝為高壓高溫的液態制冷劑。該高壓高溫的液體制冷劑再經電子膨脹閥節流降壓后，變成低壓低溫的液態制冷劑進入蒸發器。低壓低溫的液態制冷劑在此吸收空調循環冷凍水的熱量，使得空調循環冷凍水的溫度由12℃降低為7℃；同時變成低壓低溫的制冷劑蒸汽，被壓縮機吸入。這樣，經過壓縮、冷凝、節流和蒸發四個熱力過程的循環，制冷劑將從低溫物體吸收的熱量不斷地傳遞到高溫熱源中去，從而達到制冷與降溫的目的[1]。

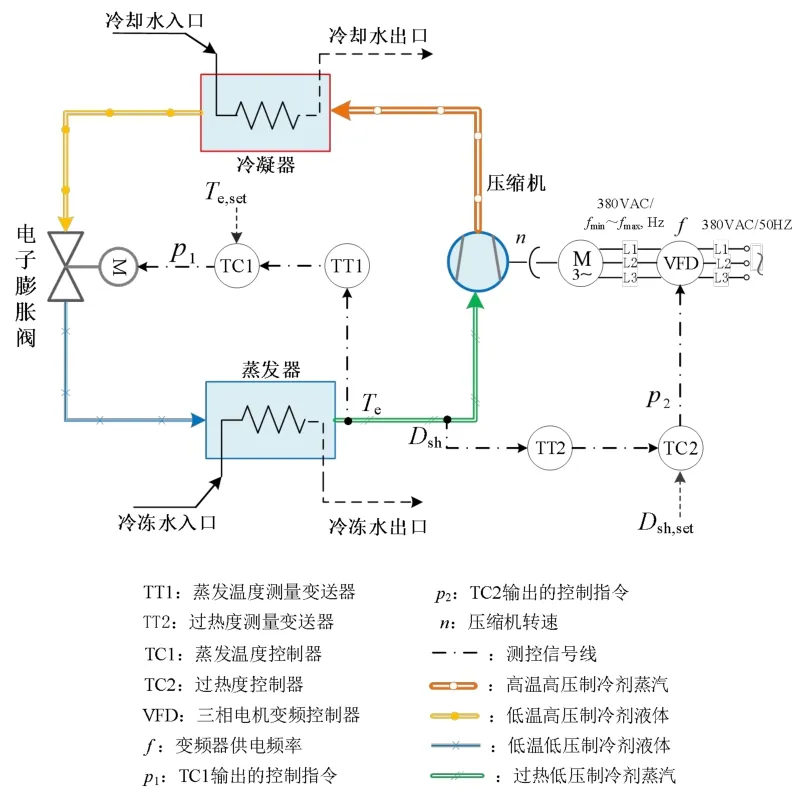
圖1 VCRU 單級制冷循環工藝的測控流程圖Fig.1 Flowchart of measurement and control for VCRU with one stage refrigeration circulating process

這里，存在關聯Te和Dsh的兩個測量、控制環路1 和2。測量、控制環路1：TT1 將反映蒸發溫度大小的標準電流信號Te傳遞給TC1，進行求偏差ΔTe=Te,set-Te，對ΔTe進行PID 運算后，輸出控制指令p1給電子膨脹閥EEV。改變其開度OEEV，動態調節流入蒸發器的液態制冷劑流量qr，使得Te≈Te,set。測量、控制環路2：TT2 將反映過熱度大小的標準電流信號Dsh傳送給TC2，先進行ΔDsh=Dsh,set-Dsh運算，然后將ΔDsh也進行PID 運算后，輸出控制指令p2給變頻器VFD。VFD 則輸出變化的供電頻率信號f，使得壓縮機的轉速n動態改變，確保Dsh≈Dsh,set。

1.2 蒸發器中的兩個控制回路的耦合作用

如上所述，表征蒸發器性能的2 個參數Te和Dsh，對應兩個控制環路：電子膨脹閥開度OEEV—蒸發溫度Te和壓縮機驅動電機的供電頻率f—過熱度Dsh。相應的被控參數Te和Dsh，記為y1和y2；相應的調節參數OEEV和f，記為u1和u2。用矩陣表示，即調節參數U=[u1u2]T，被控參數Y＝[y1y2]T

由于存在耦合效應。可借助矩陣分析法，建立這兩個控制回路的耦合傳遞函數矩陣。故兩個控制回路的耦合傳遞函數關系可表示為Y＝Gi,j(s)U。這里，Gi,j(s)(i=1,2;j=1,2)表示第j個調節參數uj與第i個被控參數yi之間的傳遞函數，如Gi,1(s)(i=1,2)表示第1 個控制回路中的調節參數u1(OEEV)分別對兩個控制回路中的被控參數y1(Te)與y2(Dsh)造成的影響。故，蒸發器中的Te和Dsh控制回路之間的耦合傳遞函數矩陣，如下式所示：

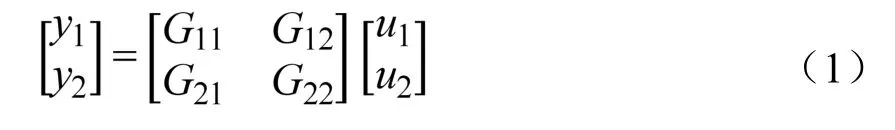
由文獻[3]中的相關數據，式（1）可改寫為：

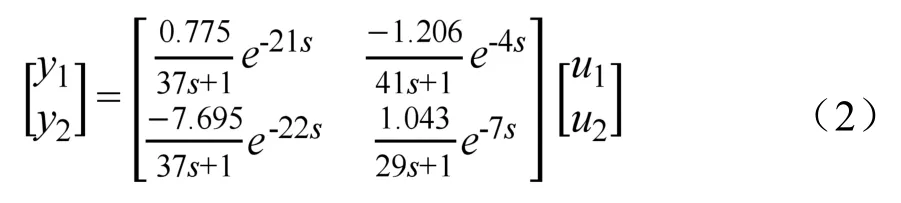
分析上式，可知第1個控制回路中的調節參數VEEV變化除了對該回路的被控參數Te產生作用外，還會影響到第2個控制回路中的被控參數Dsh。同時，第2個控制回路中的調節參數f變化除了對該回路的Dsh產生作用外，也會對第1個控制回路中的Te存在著影響。因此該耦合效應會使得Te=Te,set和Dsh=Dsh,set的預期控制效果下降。

1.3 雙參數前饋解耦PID 控制系統

針對上述2個控制回路之間出現的相互影響，本研究采用前饋補償控制的方式對該2個控制回路進行解耦，使之成為兩個獨立的無相互影響的參數PID控制系統。基于不變性原理[14]，考慮Te和Dsh控制回路之間控制量U與被控量Y的相互作用，相應的蒸發器雙參數前饋解耦補償器的傳遞函數Fij(s)(i=1,2;j=2,1)，如式（3）所示。

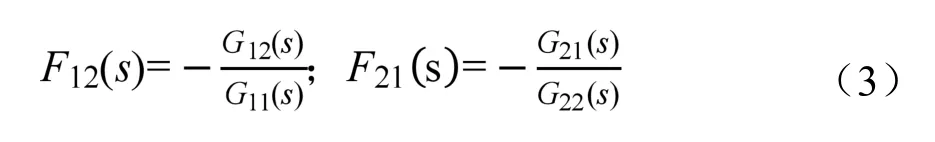
將式（3）所示的前饋解耦補償器Fij(s)與蒸發溫度和過熱度的PID控制回路相綜合，本文提出的雙參數前饋解耦PID控制系統，如圖2所示。

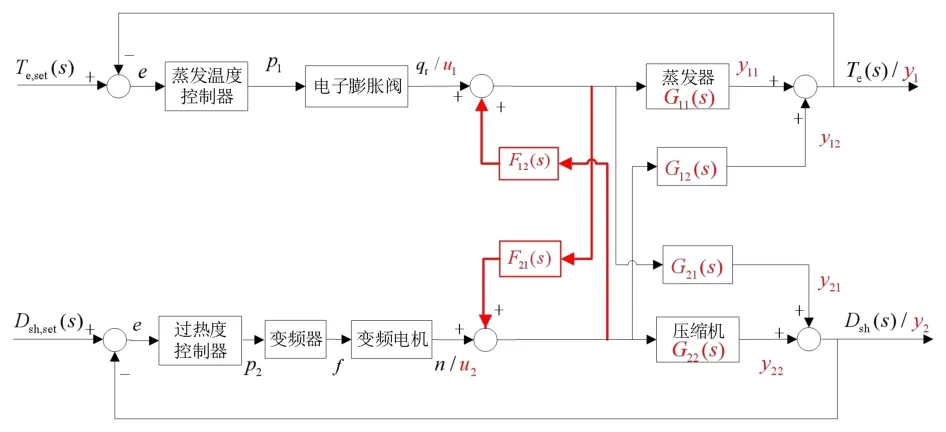
圖2 雙參數前饋解耦PID 控制系統方框圖Fig.2 Block diagram of two-parameter feedforward decoupling PID control system

這樣，通過解耦補償器F12與F21的添加，可消除一個控制回路中的控制量uj(j=1,2)對另一個控制回路中的被控量yi(i,j=12)的耦合影響，使之成為兩個獨立的控制回路。即，蒸發溫度PID控制系統通過操縱電子膨脹閥開度OEEV，改變進入蒸發器的液態制冷劑流量qr，實現Te=Te,set的制冷工藝目的；而不會對Dsh產生影響。過熱度PID控制系統通過操縱壓縮機驅動電機的供電頻率f，改變壓縮機轉速n，滿足Dsh=Dsh,set的制冷工藝需要；同樣不會對Te產生影響。

2 改進的多目標人工魚群算法及其PID控制器參數的整定

2.1 多目標優化原理

多目標優化是對多個所設計的目標函數同時進行優化，獲取這些目標函數的最佳值。然而，這些被同時優化的目標函數之間往往是相互沖突的，不能同時達到最優，因此在多目標優化過程中會在多個目標問題之間尋求一個平衡值，從而得出這些目標函數的Pareto最優解[15]。

一般而言，具有r個目標的多目標問題優化，相應的最小化求解，如式（4）所示[12]：

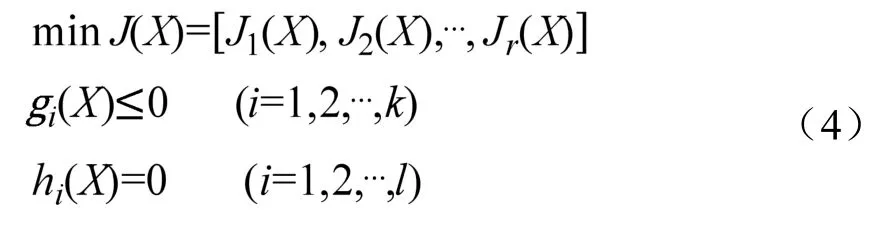
式中，X=(x1,x2,…,xn)為決策向量，其中n為決策變量數；gi(X)≤0為不等式約束；hj(X)=0為等式約束；r為目標數量；i為約束個數；J為目標函數。

2.2 改進多目標人工魚群算法

（1）改進單目標人工魚群算法

人工魚群算法是一種基于模擬魚群行為的優化算法，基本型單目標人工魚群算法BSO AFSA隨機、覓食、聚群、追尾行為如式（5a）—（5d）所示[16]：

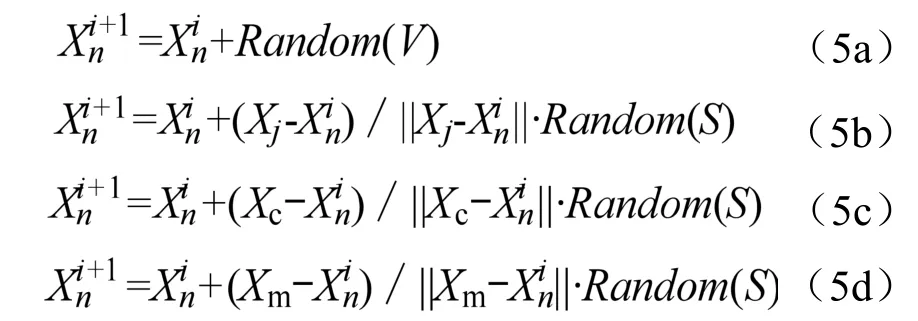
式中：i為迭代次數；n為人工魚；為人工魚的當前狀態；為執行行為后狀態、Random(V)為隨機視野；Random(S)為隨機步長；Xj為執行覓食行為：隨機視野范圍內搜索的任意狀態；Xc為聚群行為：領域中人工魚的中心位置狀態；Xm為追尾行為：領域中人工魚的最優狀態。

由于視野V和步長S是人工魚群算法中是兩個重要參數，直接影響著魚群的活動行為選擇。然而，固定的V和S會導致BSOAFSA 的求解易陷入局部最優，且收斂速度和尋優精度降低[16]。故本文對BSOAFSA 中的V和S進行適當改變，即V和S隨著i的增加，而指數遞減；其他參數不變，構建改進單目標人工魚群算法（Modified Single Objective Artificial Fish Swarm Algorithm,MSOAFSA）。修正的V和S表達式如下：

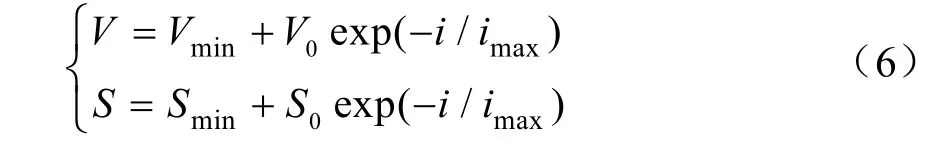
式中，V0、Vmin為視野的初始值與最小值，V∈[0.01,10][17]；S0、Smin為步長的初始值與最小值，S∈[0.002,2][17]；i為當前迭代次數；imax為最大迭代次數，一般imax≥100[17]。

所以，基于BSOAFSA 和式（6），本文重構的MSOAFSA 流程如下：

Step 1：MSOAFSA 的適應度函數f(X)設為minf(X)，相關參數初始化設置，包括人工魚規模N、人工魚維度D、V0與Vmin、S0與Smin、當前迭代次數i、最大迭代次數imax、擁擠度因子δ、嘗試次數T、變量變量Variable；

Step 2：初始化人工魚群的狀態Xn；

Step 3：對每個人工魚進行適應度函數值fitness[n](n=1,2,…,N)的計算，并找出最優人工魚Xb；

Step 4：基于式（6），進行V與S自適應更新；

Step 5：將人工魚Xn進行聚群行為，找出視野范圍內的中心位置。若擁擠度D[Xc]＜D[Xn]，且fitness[Xc]＜fitness[Xn]，則輸出聚群行為后的人工魚Xs，并向前移動一個步長。反之，則進行覓食與隨機行為，繼續搜索聚群行為下的最優狀態Xs；

Step 6：將人工魚Xn進行追尾行為，找出在視野范圍內最小適應度個體Xm。若擁擠度D[Xm]＜D[Xn]，且fitness[Xm]＜fitness[Xn]，則輸出追尾行為后的人工魚Xf，并向前移動一個步長。反之，則進行覓食與隨機行為，繼續搜索追尾行為下的最優狀態Xf；

Step 7：對比聚群與追尾行為中的最優狀態Xs與Xf，若fitness[Xf]＜fitness[Xs]，則輸出Xf替換Xb。反之，則輸出Xs替換Xb；

Step 8：若i＜imax，則返回Step 3，繼續迭代運算。否則運算結束，輸出最優適應度值fitness*。

該MSOAFSA 可用MATLAB 軟件進行編程，命名與保存為一個MSOAFSA.m 文件。選取文獻[18]中的Rastrigin 函數，數學式如下：

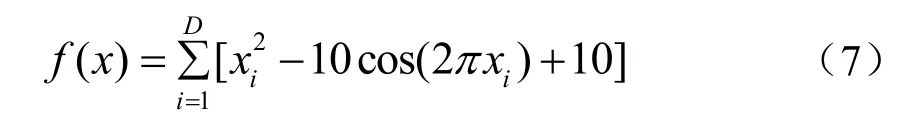
式中，xi∈[-5.12,5.12]，f(x)是多峰函數，理論極小值點在(x1,x2,…,xD)=(0,0,…,0)處取0。

將該MSOAFSA 和BSOAFSA[17]分別作用于Rastrigin 函數，進行minf(x)優化結果對比。這里，MSOAFSA 與BSOAFSA 相關參數設置為：V∈[0.01,10]、S∈[0.002,2]、imax=100、N=200、δ=15、T=100、D=10、Variable∈[-10,10]。BSOAFSA 中的V=5、S=2。兩種算法分別運行10 次，相應的統計結果和minf(x)在MSOAFSA 和BSOAFSA 作用下的變化進程，分別如表1 和圖3所示。

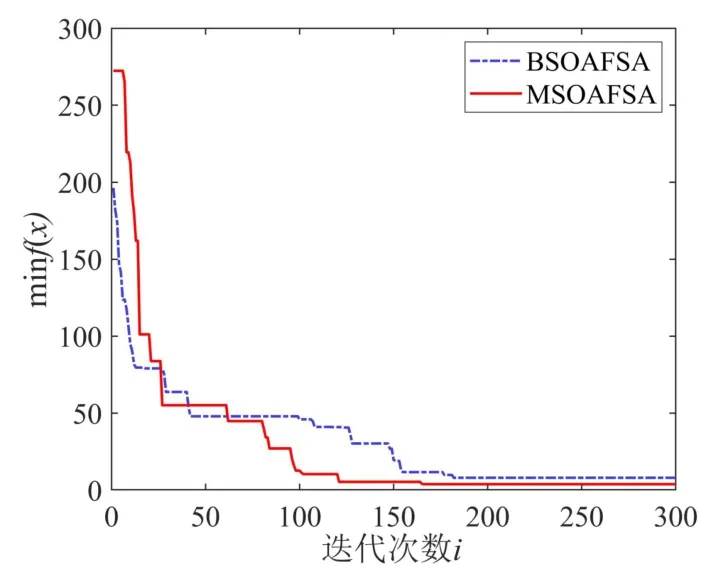
圖3 基于MSOAFSA 和BSOAFSA 的Rastrigin 函數適應度值進化過程Fig.3 Evolution process of Rastrigin function fitness value based on MSOAFSA and BSOAFSA

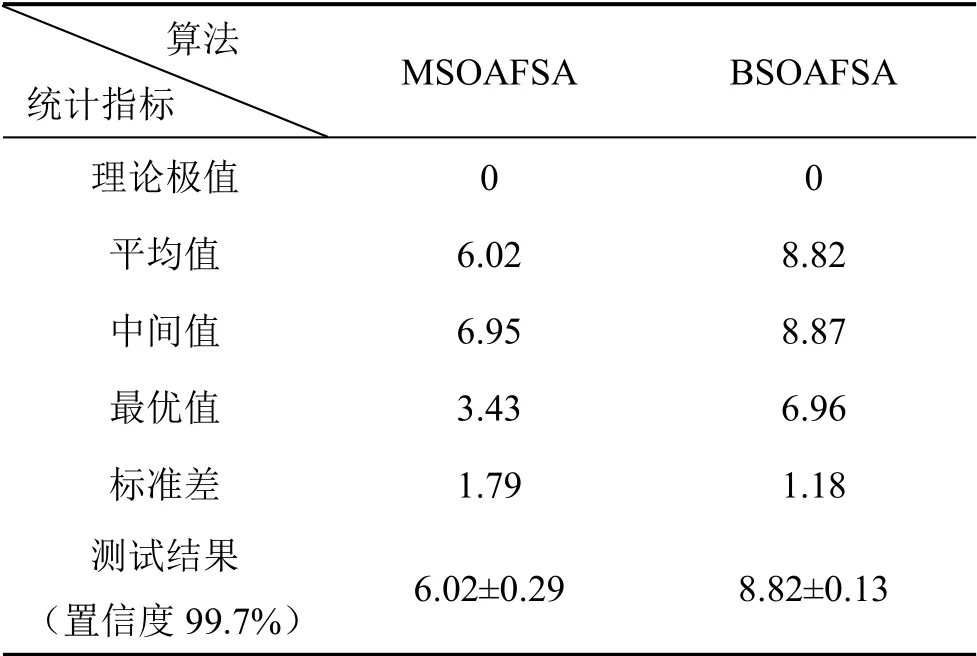
表1 MSOAFSA 和BSOAFSA 對Rastrigin 函數優化結果Table 1 Optimization results of Rastrigin function by MSOAFSA and BSOAFSA

分析表1 和圖3，相比BSOAFSA，本文重構的MSOAFSA 可以使Rastrigin 函數適應度值更接近理論值。BSOAFSA 雖在早期收斂速度較快，但在后期明顯差于MSOAFSA，這也說明了對人工魚視野和步長進行動態調整的必要性，也表明了MSOAFSA 是可行的。

（2）改進多目標人工魚群算法

為了使用人工魚群算法求解多個目標問題的Pareto 最優解，本節將基于多目標的混沌局部搜索策 略[19]（Multi-objective Chaotic Local Search Strategy,MOCLSS）引入MSOAFSA，形成改進多目標人工魚群算法（Modified Multi-objective Artificial Fish Swarm Algorithm,MMOAFSA），相應的運算流程如下：

Step 1：初始化設置：對V0、S0、Vmin、Smin、imax、N、δ、T和混沌搜索最大迭代次數Gmax、映射參數r、變量Variable 進行賦值；

Step 2：計算每個人工魚個體的目標函數J(X)，并進行快速非支配排序（FNDS），找出非支配解（NDS），存放在外部檔案集（Rep）中；

Step 3：開始優化，由式（6）自適應更新V、S，對其執行的行為進行選擇，包括：覓食Pray、聚群Swarm、追尾Follow 和隨機行為Move，并將其通過FNDS，找出NDS，與上次生成的Rep 進行合并，生成(Rep)New；

Step 4：對合并后的(Rep)New，再次進行FNDS，并對其進行維護：若Rep>N，則進行Dis 計算，并按照降序排列選取前100個個體，完成Rep的更新；

Step 5：通過基于多目標的混沌局部搜索策略，再次更新Rep；

Step 6：若i≥imax，則停止算法，輸出最終Rep作為Pareto 最優解x*。否則，返回Step 3 迭代繼續。

同樣的，上述MMOAFSA也可用MATLAB軟件進行編程，命名與保存為一個MMOAFSA.m文件。選取文獻[20]中的ZDT1、ZDT3和DTLZ2測試函數，分別將該MMOAFSA 和文獻[15]中的MOAFSA(也編程、命名與保存為一個MOAFSA.m文件)作用于它們。這里，MMOAFSA和MOAFSA相關參數設置為：V∈[0.01,5]、S∈[0.002,1.2]、

imax=200、N=200、δ=15、T=100、Gmax=10、r=4、

Variable∈[0,1]，MOAFSA中的V=2、S=0.5。

假設網絡中每個節點的測量噪聲{vk,i}和輸入矢量{uk,i}是相互獨立的,則可以得到且有以下給出了加權最大似然估計問題(等價于加權最小二乘估計問題)的解:

此外，選擇5 個性能指標[20]：世代距離（Generational Distance,GD ）、反 世 代 距 離（Inverted Generational Distance,IGD）、超體積（Hypervolume,HV）、均勻性（Spacing,SP）和多樣性（Diversity,DIV）來定量分析兩種算法的優化性能。其中，GD表示非支配解到Pareto最優解的平均距離、而IGD為GD的逆向映射，其值越小，表明優化解越接近于參考解且算法收斂性越好；HV值表示非支配解集與參照點圍成的目標空間中區域體積，其值越大說明算法的綜合性能更強；SP為每個解到其他解的最小距離標準差，其值越小，說明解集越均勻；DIV值反應解的多樣性，值越小，解的多樣性越高。

MOAFSA與MMOAFSA分別運行10次，圖4和表2分別為這兩種算法對上述3個測試函數的優化過程和基于5個性能評價指標的結果統計，括號內代表MOAFSA[15]的優化結果。

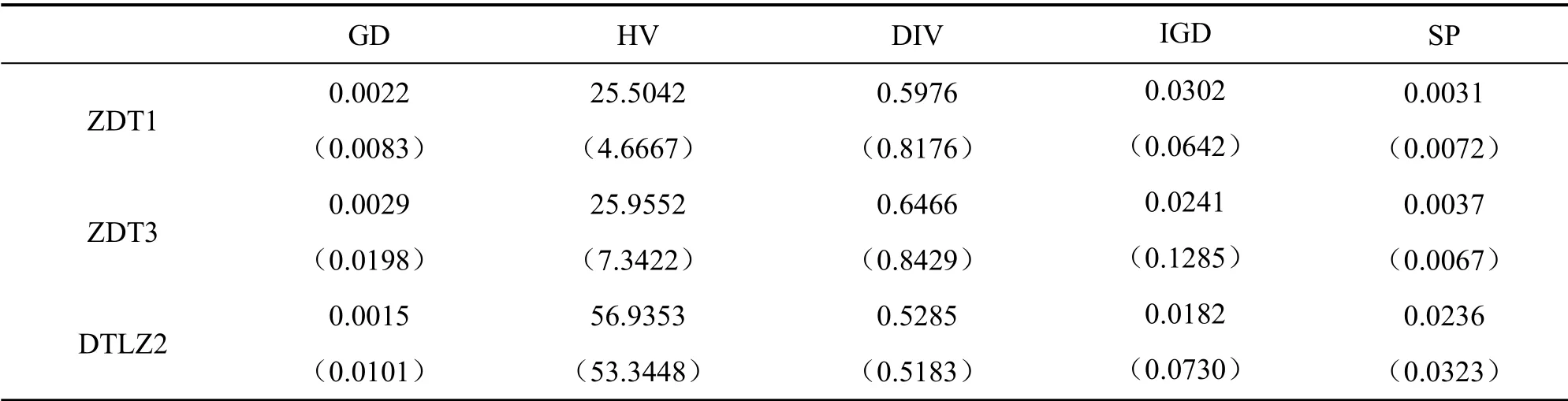
表2 MMOAFSA 與MOAFSA[15]性能指標結果Table 2 Performance index results solved by MMOAFSA and MOAFSA

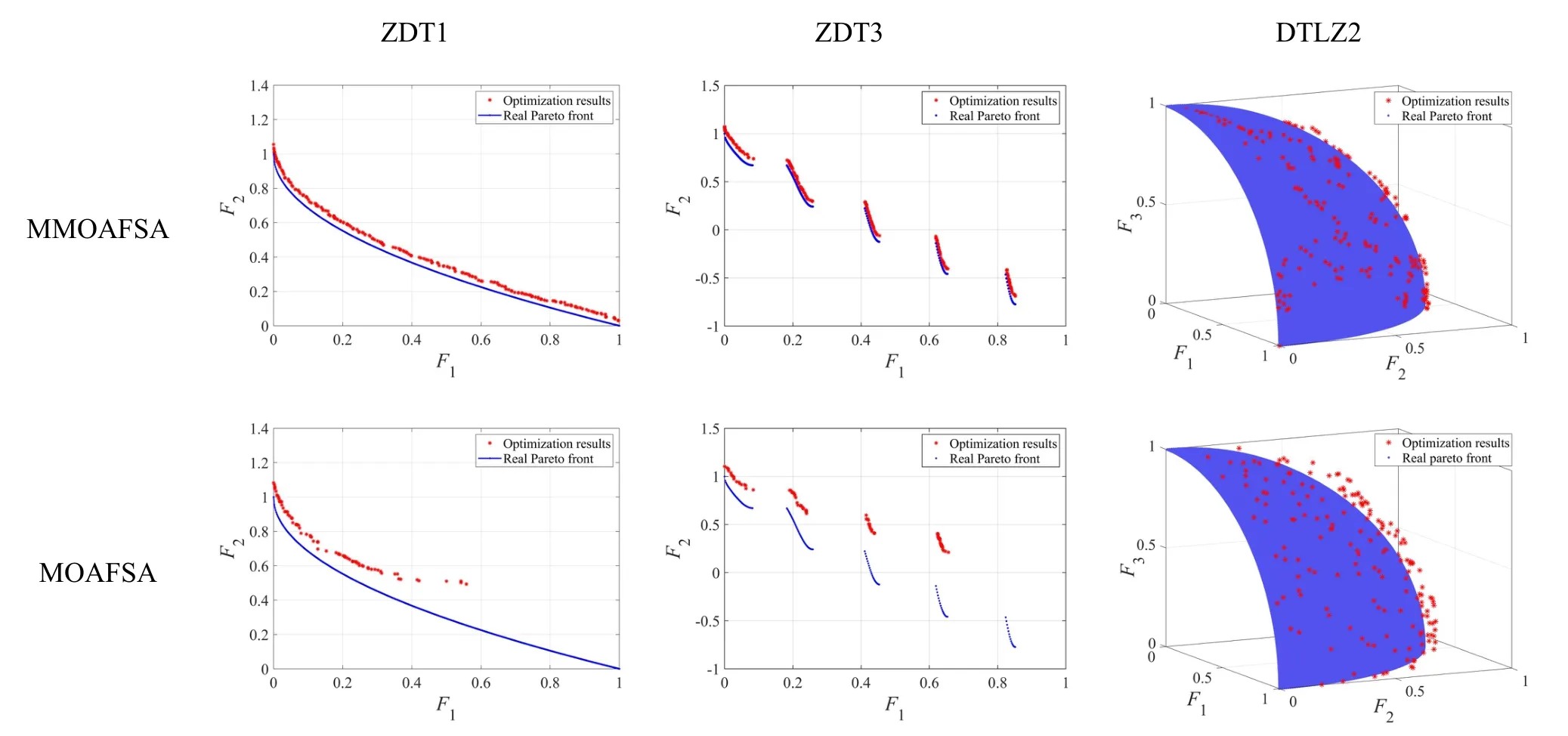
圖4 MOAFSA[15]和MMOAFSA 對ZDT1、ZDT3、DTLZ2 測試函數的優化過程Fig.4 Optimizing processes solved by MOAFSA and MMOAFSA for the test functions of ZDT1,ZDT3 and DTLZ2

由圖4可知，當MOAFSA與MMOAFSA對兩目標和三目標函數的問題進行優化時，最后均可收斂到相應的真實Pareto前沿區域。但后者求解變化與真實Pareto前沿變化之間的偏離度更小，且所求解的非支配解更貼近Pareto前沿，收斂性更好。

分析表2，可知MMOAFSA求解的HV平均值大于MOAFSA，表明其綜合性能優于MOAFSA。對于其他4項指標平均值，MMOAFSA的解均小于MOAFSA，表明MMOAFSA得到的非劣解相比MOAFSA更接近Pareto前沿面，算法的收斂性及解的多樣性均優于MOAFSA。所以，該MMOAFSA的改進思路是可行、有效的，為后面PID控制器參數整定算法的設計，奠定了堅實的基礎。

2.3 基于MMOAFSA 的PID 控制器參數整定算法

本節選擇ITAE、tc和Ess[8]作為MMOAFSA的三個目標函數：

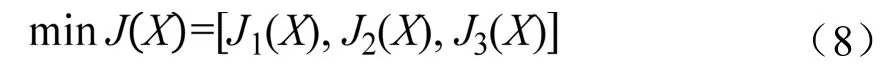
Step 1：根據Z?N 整定法的PID 控制器參數整定公式，計算出PID 控制器參數的初始值y0=[KP0,KI0,KD0]，置入基于MALAB/Simlink 工具組態中的PID 控制器，且設定變量KP、KI和KD的上、下限；

Step 3：輸入單位閉環負反饋PID 控制系統的反饋信號e(t)，基于minJ(X)，計算每個魚群個體的適應度值[J1,J2,J3]；

Step 4：增大i，由式（6）自適應更新人工魚的V和S，并對其進行行為選擇。同時通過FNDS，不斷輸出每一組NDS，即yi；

Step 5：對NDS，進行MOCLSS，并更新輸出搜索結果NDS。同時輸出對應的閉環負反饋PID控制系統動態響應；

Step 7：當i≥imax，停止運算。輸出PID 控制器參數最優值y*=[KP*,KI*,KD*]，ITAE、tc和Ess的Pareto 最優解以及相應的閉環負反饋PID 控制系統動態響應。否則，返回Step 3。

需要說明的是，可用MATLAB軟件，將上述的PID控制器參數整定流程進行編程，保存為一個獨立程序，命名為MMOAFSA.m。該MMOAFSA.m是與組態的閉環PID負反饋控制系統同步運行的。

選用文獻[11]中的二階傳遞函數，如式（9）所示，作為被控對象設計一個單位閉環PID 負反饋控制系統作用于它。

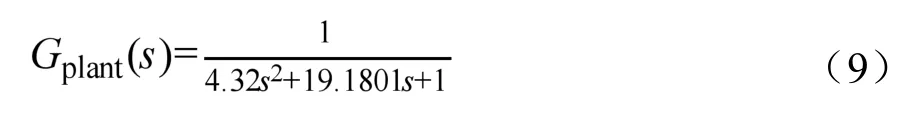
首先借助MATLAB/Simlink工具，進行上述的單位閉環PID負反饋控制系統的組態。其次，分別用MOAFSA[15]、MMOAFSA和Z－N法來整定該PID控制器的3個參數。其中MOAFSA[15]也將minJ(X)作為其目標函數，它與MMOAFSA相關的參數設置為：N=30、imax=30、V∈[0.01,2]，S∈[0.002,1]、δ=15、T=100、Gmax=10、r=4、KP∈[2,5]、KI∈[0.1,0.5]、KD∈[0.2,0.5]。最后，Z－N法離線計算出PID控制器參數值。再依次同步運行MOAFSA.m和單位閉環PID 負反饋控制系統組態模型，MMOAFSA.m和單位閉環PID負反饋控制系統組態模型。可獲取該PID控制器的3個參數整定結果，如表3所示。

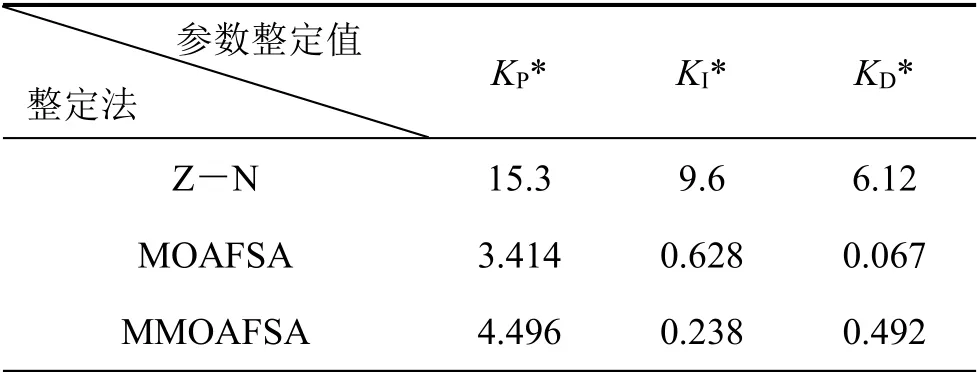
表3 PID 控制器參數整定的結果Table 3 Results of tuning three parameters for PID controller

相應的閉環負反饋PID控制系統動態響應曲線，如圖5所示。

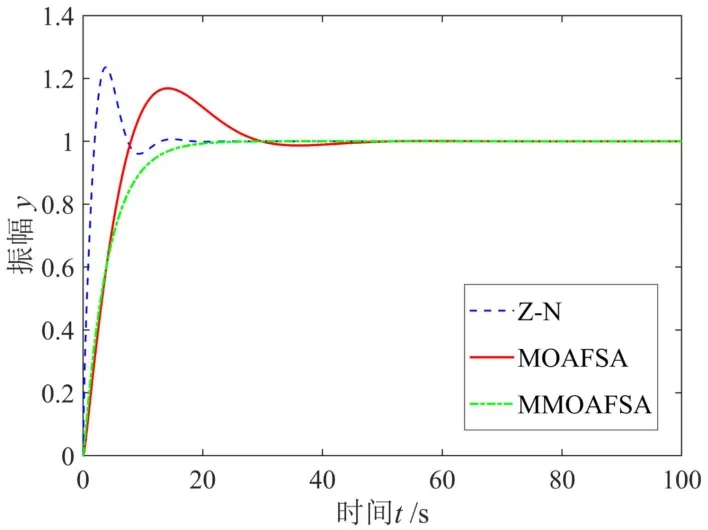
圖5 不同PID 控制器參數值的單位閉環負反饋控制系統動態響應Fig.5 Dynamic responses of a unit closed-loop negative feedback PID control system with different values of controller’s parameters

分析圖5 可知，基于MMOAFSA 整定的KP*,KI*,KD*，其閉環PID 控制系統的性能指標，如最大偏差、超調量和誤差等，均好于由Z－N 法和MOAFSA 參數整定作用下的閉環PID 控制系統的性能指標，表明MMOAFSA 對PID 控制器的參數整定是可行的。

3 數值仿真

3.1 雙參數前饋解耦PID 控制系統中的組成環節的輸入/輸出特性

（1）蒸發器的輸入/輸出特性

蒸發器這一被控對象為一階慣性、時滯的環節，其輸入/輸出特性為：通過電子膨脹閥后的制冷劑流量qr/蒸發溫度Te，傳遞函數如下[3]。

（2）壓縮機的輸入/輸出特性

壓縮機同樣為一個一階慣性、時滯的環節，其輸入/輸出特性為：變頻電機輸出的電機轉速n/過熱度Dsh，傳遞函數如式（11）所示[3]。

（3）電子膨脹閥的輸入/輸出特性

具有線性流量特性的電子膨脹閥，可連續改變其開度OEEV來調節制冷劑流量qr。因此它的傳遞函數如下[21]：

（4）變頻器的輸入/輸出特性

在工程實踐中，變頻器傳遞函數可簡化以設定為一個比例環節[22]。

式中，f為變頻器輸出的供電頻率，Hz；U為輸入的電壓控制信號，V。

（5）變頻電機的輸入/輸出特性

通過文獻[22]，可知變頻電動機為一個一階慣性環節，其輸入/輸出特性為：變頻器輸出頻率f∕轉速n，傳遞函數如下所示：

式中，KM為穩態轉速與供電頻率的比值；TM為電機拖動系統的時間常數，取值為電機啟動時間的四分之一。

（6）蒸發溫度、過熱度PID 控制器的輸入/輸出特性

在蒸發溫度與過熱度兩個控制回路中均選擇簡單、形式固定、操作便捷的PID 控制器。相應的傳遞函數表示如下[10]：

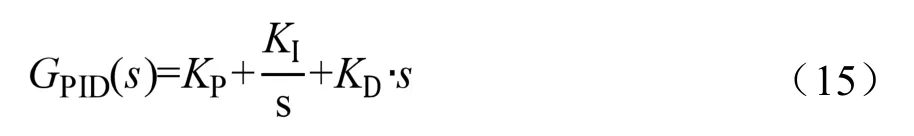
式中，KP、KI、KD為控制器的比例增益、積分增益、微分增益。

（7）蒸發溫度、過熱度測量變送器的輸入/輸出特性

測量變送器在過程控制中是必不可少的組成部分，蒸發溫度和過熱度測量變送器分別作用于這兩個控制回路中的反饋通道上。蒸發溫度和過熱度測量測量變送器均視為比例環節[5]，對應的傳遞函數分別為H1(s)=1，H2(s)=1。

3.2 雙參數前饋解耦PID 控制系統的組態與仿真

考慮到蒸發器與壓縮機的被控對象具有時滯特性，引入Smith 預估器[6]，來消除時延帶來的影響，提升系統的控制品質，同時，設置前饋補償解耦器F12(s)和F21(s)，實現對VCRU 雙參數的解耦控制。所以，基于MMOAFSA 的蒸發溫度與過熱度前饋補償解耦PID 控制系統，如圖6所示。

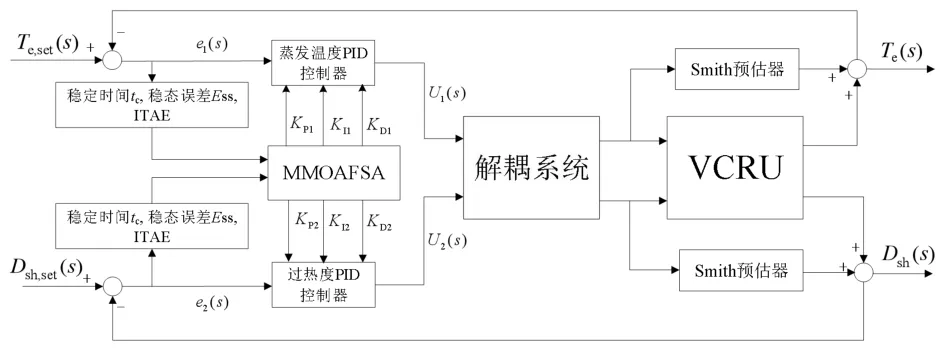
圖6 基于MMOAFSA 的蒸發溫度與過熱度前饋解耦PID 控制系統方框圖Fig.6 Block diagram of two-parameter feedforward decoupling PID control system based on MMOAFSA

基于min(ITAE,tc,Ess)，通過MMOAFSA對兩個控制回路中的PID控制器6個參數（KP1,KI1,KD1,KP2,KI2,KD2）進行尋優整定，獲取PID控制器參數最優解及三目標函數值，使得Te,set≈Te，Dsh,set≈Dsh，滿足制冷工藝的要求。

基于圖6 和Simulink 工具，構建出該雙參數前饋解耦PID 控制系統的Simulink 模型，如圖7所示。夏季制冷工況下的空調冷凍水進/出口溫度為12℃∕7℃，而蒸發溫度一般較冷凍水出口溫度低2℃～4℃，且過熱度范圍為5℃～10℃[1]。因此，設置蒸發溫度初始、終止值分別為3℃、5℃，即Te,0=3℃、Te,set=5℃；過熱度初始、終止值分別為8℃、6℃，即Dsh,0=8℃、Dsh,set=6℃。

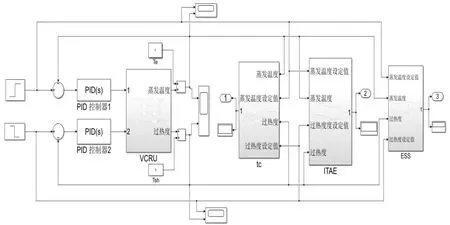
圖7 基于MMOAFSA 的雙參數前饋補償解耦PID 控制系統Simulink 模型Fig.7 Simulink model of two-parameter feedforward decoupling PID control system based on MMOAFSA

因此，在MATLAB 中的Command Window 界面和Simulink 環境，MMOAFSA.m 參數設置同上述2.3 中一樣，非支配解的規模設定為3，變量范圍調整為：KP1，KP2∈[0.7,1]、KI1，KI2∈[0.05,0.08]、KD1，KD2∈[0.02,0.06]。同步運行MMOAFSA.m 和圖7所示的Simulink 模型，該MMOAFSA 得到的蒸發溫度、過熱度PID 控制器參數及其對應的ITAE、tc和Ess的3 組Pareto 最優解，列于表4。

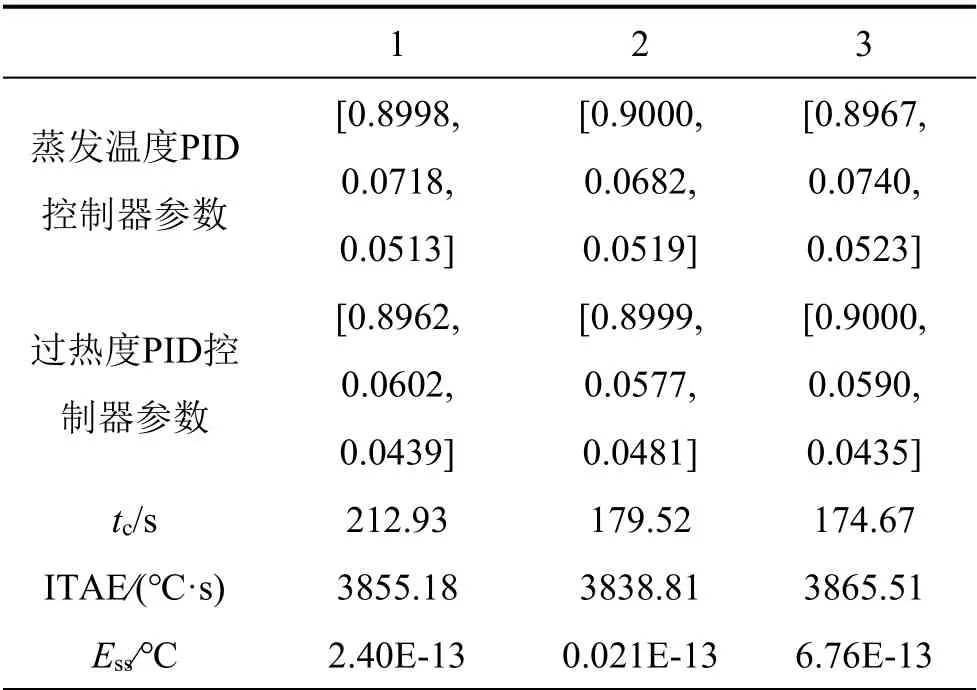
表4 蒸發溫度、過熱度PID 控制器參數及其三目標函數的Pareto 解Table 4 Pareto solutions of parameters of PID controllers for evaporation temperature and degree of superheating and three objective functions

從表4可看出三組Pareto解及其對應的三個目標函數值存在互相沖突的地方，每組解都表現出不同的特征，例如，第3組的tc最小，但ITAE與Ess卻大于另外兩組解。由此看出，在多目標優化整定控制器參數過程中可以獲得側重點不同的控制效果，以供不同的控制需求使用。

相應的ITAE、tc和Ess的優化過程，如圖8所示。

圖8 ITAE,tc,Ess的尋優過程Fig.8 Optimization process for ITAE,tc and Ess

由圖8可清楚地看出不同Pareto解所對應的三個目標函數值之間的關系，在曲面上不同的位置都反應出不同的控制特征。

同時，空調夏季工況下，基于蒸發溫度、過熱度PID控制器參數的3組Pareto最優解，可得到蒸發溫度、過熱度的動態響應過程，分別如圖9和10所示。

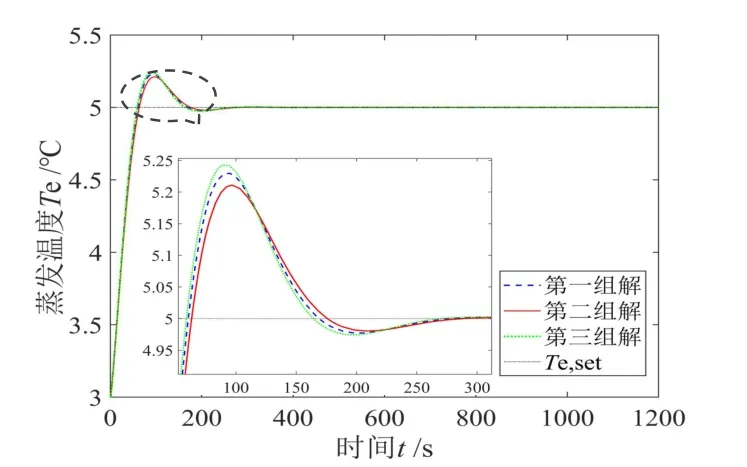
圖9 三組Pareto 最優解下的蒸發溫度動態響應Fig.9 Dynamic responses of evaporation temperature under three Pareto optimal solutions

分析圖9和10可知，基于MMOAFSA得到的兩個PID控制器的三組解均可使蒸發溫度與過熱度達到較好的控制效果。但從局部放大部分可看出，每組解在其調節時間、超調量都表現出不同的差異，且與表4中三目標函數值所反應出的特征相對應。

3.3 與其他控制方式的比對

此外，選擇Z?N 整定法和MOAFSA，也對相同的蒸發溫度與過熱度PID 控制系統中的兩個控制器參數進行整定和輸出Te和Dsh的動態響應，且與MOAFSA 進行對比分析，如圖11 和12所示。

分析圖10 和圖11，可知采用MMOAFSA 的PID 控制器參數整定方式，蒸發溫度與過熱度響應曲線的性能均優于其他兩種方式。Z?N 整定法，雖然調節時間縮短，但表現出了較大的超調量和震蕩頻率。相比MOAFSA，MMOAFSA 使得Te和Dsh的調節時間和超調量均有一定的減小，提升了控制品質。

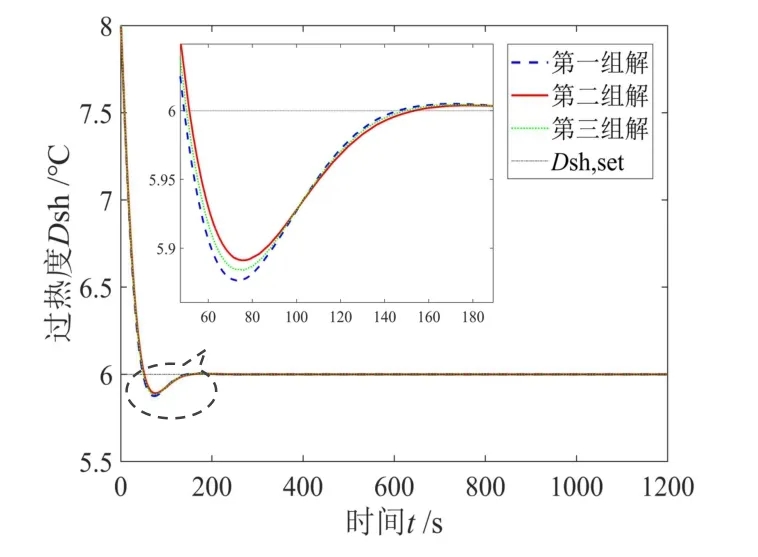
圖10 三組Pareto 最優解下的過熱度動態響應Fig.10 Dynamic responses of degree of superheating under three Pareto optimal solutions

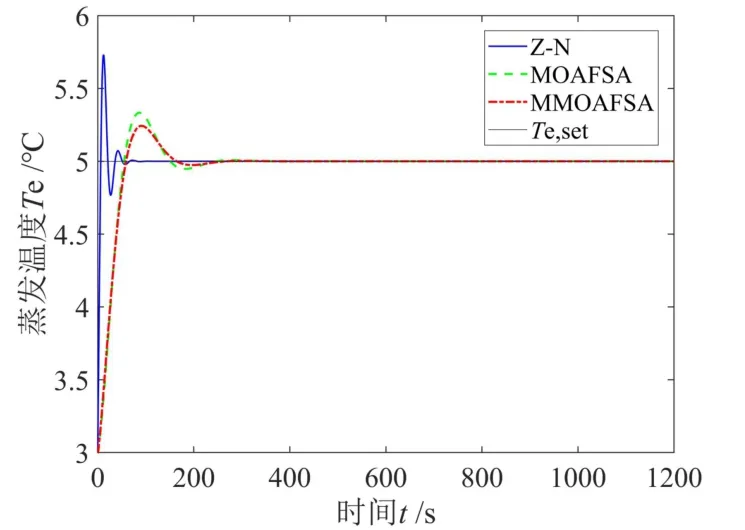
圖11 三種PID 控制器參數整定方式下蒸發溫度響應曲線Fig.11 Dynamic responses of evaporation temperature under three modes of tuning parameters of PID controller

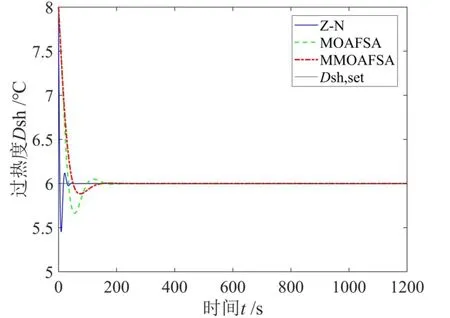
圖12 三種PID 控制器參數整定方式下過熱度響應曲線Fig.12 Dynamic responses of degree of superheating under three modes of tuning parameters of PID controller

4 結論

針對VCRU中的蒸發溫度與過熱度被控對象，本文提出了一種基于MMOAFSA的雙參數前饋補償解耦PID控制策略。首先，通過對人工魚的視野和步長同時進行非線性改變，重構了MSOAFSA，且基于Rastrigin函數測試，驗證了該算法改進的可行性。其次，將基于多目標優化的混沌局部搜索策略引入MSOAFSA，形成MMOAFSA。通過ZDT1、ZDT3和DTLZ2三個測試函數和GD、IGD、DIV、SP、HV五個評價指標，可看出MMOAFSA在收斂性、分布性、多樣性等均優于MOAFSA。進而將min(ITAE,tc,Ess)作為MMOAFSA的目標函數，形成PID控制器參數的整定算法。同時，構建前饋解耦補償器的傳遞函數矩陣，來消除蒸發溫度Te和過熱度Dshh這兩個控制回路之間的耦合效應。最后，構建Te和Dsh前饋解耦PID控制系統，對于Te和Dsh回路中兩個PID控制器中的6個參數，應用MMOAFSA進行尋優整定，獲取了其最佳值及ITAE，tc，Ess的PF解。滿足Te=Te,set和Dsh=Dsh,set的制冷工藝目的，且調節時間、超調量和震蕩頻率都有著明顯的改善，控制質量顯著提升。