Design of an all-dielectric long-wave infrared wide-angle metalens
Ning Zhang(張寧), Qingzhi Li(李青芝), Jun Chen(陳駿), Feng Tang(唐烽),Jingjun Wu(伍景軍), Xin Ye(葉鑫), and Liming Yang(楊李茗)
Research Center of Laser Fusion,China Academy of Engineering Physics,Mianyang,Sichuan 621900,China
Keywords: long-wave infrared,all-dielectric metasurface,aberrations,metalens
1. Introduction
Metamaterials are typical artificial structural materials based on subwavelength structures (also called metaatoms).[1–3]They utilize the singular electromagnetic response of a designed subwavelength structure to achieve electromagnetic parameters or properties that do not exist in nature. Metalenses are two-dimensional metamaterials[4–6]in which the thickness dimension is ignored. Metamaterials themselves can be used to guide and control the flow of electromagnetic waves. The ultra-thin,flexible nature of metasurfaces enables them to modulate light. Metalenses are products that combine all the above excellent characteristics and they have attracted intensive attention from researchers.[7,8]
In recent years most work on metalenses has concentrated on high-efficiency focusing of visible and near-infrared light.[9]Yuet al.and Niet al.achieved near-infrared phase control by using V-shaped antennas.[10,11]This research approach and method opened up our understanding of optical devices. Porset al.designed a flat mirror that focused a linearly polarized incident beam with a theoretical focusing efficiency of 78% in a broadband wavelength regime from 700 nm to 1000 nm, while the experimental broadband focusing efficiency reached approximately 30%.[12]Capasso and co-workers fabricated and designed high-aspect-ratio alldielectric (titanium dioxide meta-atoms and silica substrate)metasurfaces as metalenses, achieving high efficiency at a wavelength of 405 nm.[13]There has been less work on longwave infrared light[14]and the actual metalenses do not work well.[15]
Most work on metalenses has been concerned with paraxial optics. However, research on wide-angle imaging and applications in optical systems is required. For example,miniature wide field-of-view (FOV) imaging systems are of considerable interest for application in both eye-tracked extraocular cameras for use in retinal prostheses and wearable visual equipment.[16,17]Wide FOV, high-resolution, compact and real-time optical imaging systems are widely used in most state-of-the-art vision applications,such as recording and tracking clouds or stars,guidance of unmanned vehicles,threat detection, situational awareness, surveillance, tracking omnidirectional threats and creative photography.[18–20]The main problem with a wide-angle optical system is coma.[21]Aietaet al.processed the metasurface on a hyperboloid. It is an enormous challenge to pattern the nanostructure on a curved surface and many researchers have proposed solutions to this problem.[22,23]The efficiency of this type of metasurface is affected by the respective efficiencies of the two metasurfaces,and the achievable field of view is limited. In summary,there is a need to achieve wide-angle imaging through a single-layer metasurface.
In the past year, multiple comparably bulky and heavy refractive lenses have been introduced to achieve wide-angle FOV imaging. They have achieved a 160°FOV in visible light.[24]Through multi-parameter optimization, the traditional method can achieve a 360°× (40°–90°) FOV in visible light, which is better than previous results.[25]However,the lens system is too large. So an imaging system which can achieve a wide-angle FOV with a single-layer lens would not only reduce the difficulty of adjusting the system but would also facilitate its miniaturization.
In summary,the need for a monolithic lens is imperative,but research on long-wave infrared wide-angle metalenses has rarely been reported. The present work uses a single-layer quadratic phase function metasurface to achieve wide-angle beam focusing.Comparison with a hyperbolic metalens shows that the quadratic metalens still maintains a good modulation transfer function(MTF)even at 120°(0.4@60 line pairs/mm).By controlling the phase through the thickness of the material the quadratic phase function has high processability on the metasurface.
2. Design and results
2.1. Design of the unit cell
With regrard to the transmission characteristics of structural units, figure 1(a) shows a schematic diagram of the arrangement of subwavelength silicon structures.D,h, andPare given adjustable parameters. Previous work[26]fixed the height of the nanopillars at 6.8 μm. Due to the subwavelength lattice constant,the array acts as a zeroth-order grating and it is entirely described by its transmission and reflection coefficients.
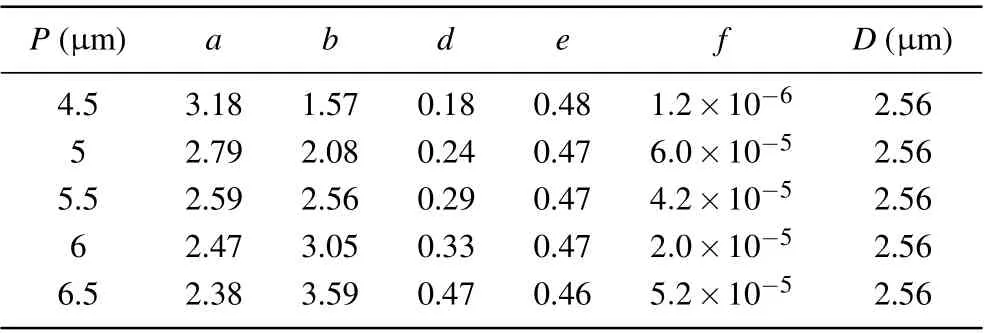
Table 1. Variable parameters.
Figure 1(b)shows the simulated transmittance and phase of the cylindrical structure as functions of the period (P) and cylinder diameter(D). The fixed height of the selected structure is 6.8 μm. The structural unit works at a wavelength of 10.6 μm but the concept is scalable to any wavelength.As shown in Fig. 1(c), light is concentrated inside the posts which behave as weakly coupled low-quality factor resonators.Therefore, the high-refraction material not only provides a flexible to 2πphase change but also weakens the mutual coupling between the structures. The radius of the nanocylinder varies from 1.5 μm to 4 μm. In all cases,the phase and transmittance change with the diameter of the cylinder, and the change in phase with cylinder diameter satisfies
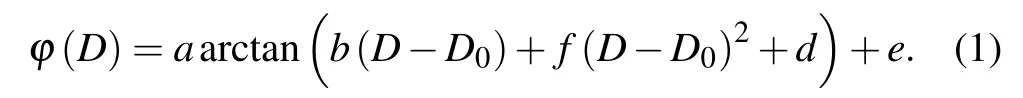
Due to the large size of the structure we adopted the waveguide theory. The phase increase required by the waveguide theory is determined by the total reflection formula. Equation(1)improves upon the total reflection formula. The coefficients of Eq. (1) are given in Table 1, and the phase changes with the diameter of the cylinder under different periodsP. The source of the improved formula depends entirely on the phase formula established in the evanescent field. When phase information is added to the total reflection interface by light, it follows Eq.(1).
2.2. Design of micro-lenses
To design a micro-lens that can implement a transmissive phase mask,we must find a family of periodic nanostructures with the same lattice but different scatterers that provide large transmission amplitudes. Their phases must span the entire to 2πrange. Such a family is shown in Fig. 1(d), where the heights of the tall posts with a diameter of 6.8 μm are varied from 1.5 μm to 4 μm in a hexagonal lattice with a 5 μm period. According to Smithet al.,[2]the traditional method of designing a micro-lens is based on the discretized phase,which causes a certain phase error,but this is not conducive to phase optimization of the lens. Using Eq.(1),we design a metalens to achieve an ideal and controllable optimization effect.
Through Fourier optics it is known that many optical phases can be focused. One such phase is the phase function calculated based on the lens curvature distribution (Eq. (2)),another is the phase function obtained by outputting an ideal spherical wave(Eq.(3)). The phase distribution of the lens is shown in Eq.(2). We define this type of lens as a type 1 metalens (hyperbolic lens). The phase is shown in Eq. (3). We define this type of lens as a type 2 metalens(quadratic lens)
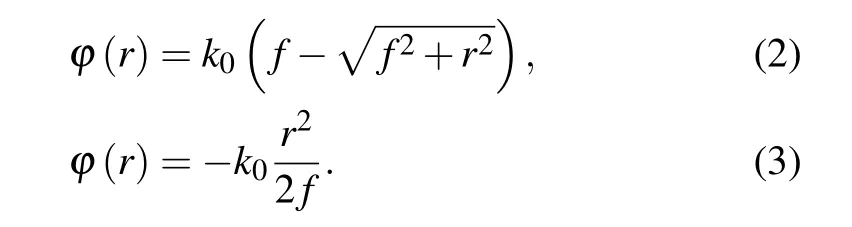
The expressions for these two types of lenses in paraxial optics are consistent. We designed a microlens with a diameter of 600 mm, a focal length of 150 mm and a high numerical aperture.
According to the generalized Snell theorem,the ray path for the two types of microlenses is solved. Figure 2(a)shows the light distribution for a two-position microlens. It can be seen from this figure that the type 2 microlens has an obvious spherical aberration. This spherical aberration is caused by the surface phase gradient. In Fig.2(d)the spherical aberration causes the focal length of the metalens to shift,and the focal spot at the focal plane becomes larger. This is the opposite effect to a type 1 metalens(Fig.2(b))with no spherical aberration. However,a type 2 microlens has a very high depth of focus and better application prospects in some laser cutting and achromatic optical systems.
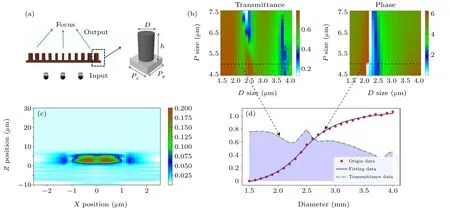
Fig.1.Simulation results for the periodic structure unit.(a)Schematic diagram of the structural unit with adjustable parameters D,h,and P.(b)The simulated transmittance and phase of the structural unit vary with the period of the structural unit and the radius of the cylinder. (c)Side view of the refractive index distribution and energy distribution of the structural unit. The black line represents the waveguide boundary.(d)When the periodic structure constant is 5 μm,the simulated transmittance and phase of the structural unit are shown. In all structures, the height of the structure is 6.8 μm and the incident wavelength λ0=10.6 μm.
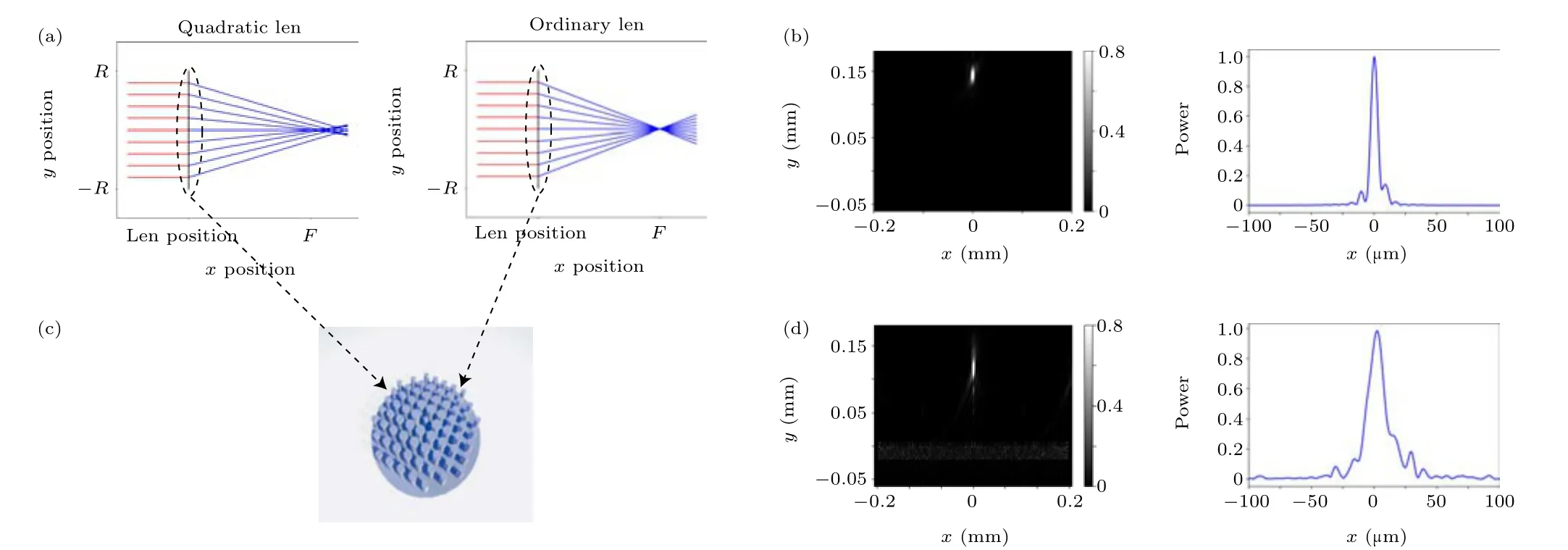
Fig.2. Parallel light incident simulation of a micro-lens. (a)Illustration of the use of a micro-lens to focus parallel light. (b)Energy distribution diagram of a type 1 micro-lens in the XZ plane and a schematic diagram of the spot size on the excitation plane(XY plane). (c)Schematic diagram of the micro-lens design;the same period structure is selected to design the metalens. (d)Energy distribution diagram of a type 2 micro-lens in the XZ plane and a schematic diagram of the spot size on the excitation plane(XY plane).
2.3. Micro-lens multi-angle results
The performance of the micro-lenses was evaluated by three-dimensional finite difference time domain(FDTD)simulations. In Figs. 3(a) and 3(c) the ray chasing method is used to solve the light distribution on the surface of the metalens.The results of geometric optics indicate that a type 1 micro-lens produces coma. As shown in Fig. 3(b), when the incident light obliquely irradiates the surface of a micro-lens a type 1 micro-lens will produce a comet-shaped spot at the focal plane. In addition,the position of the spot will vary greatly with the angle of incidence. However,a type 2 micro-lens can eliminate the coma aberration. As shown in Fig. 3(d), as the angle of incident light increases to 60°it can still generate a focal spot of wavelength size. The focal position produced by the second type of lens isx=fsin(θ), wherefis the focal length andθis the angle of incidence.
Coma aberration will further reduce the image resolution.As shown in Fig 4(a),coma aberration causes the focal plane spot to oscillate,and the focal spot becomes larger. As the angle of incidence becomes larger,the focal point moves farther and farther away from the center. In contrast, the microlens shown in Fig. 4(b) can correct spherical aberration well, and the focal point moves closer to the center. Compared with a type 1 micro-lens, a type 2 micro-lens can be used in some wide-angle imaging systems. The aberration that occurs at 75°is limited by the numerical aperture of the optical system.By adjusting the numerical aperture of the optical system,this aberration can be eliminated. In theory, a FOV angle greater than 120°can be realized.
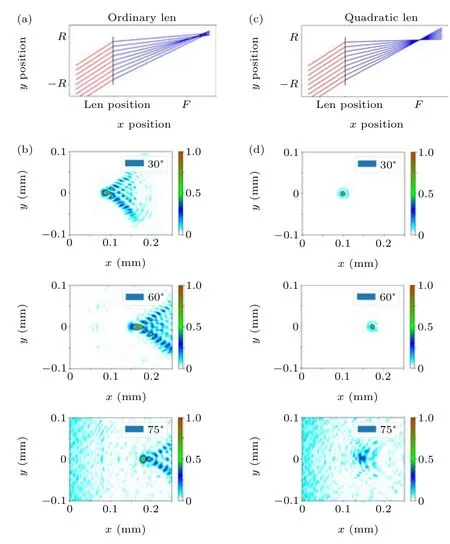
Fig. 3. Micro-lens multi-angle results. (a) Schematic diagram of the performance of an obliquely illuminated type 1 micro-lens. (b)Oblique illumination of a type 1 micro-lens produces coma. (c)Schematic diagram of the performance of an obliquely illuminated type 2 micro-lens. (d) Schematic diagram of a focal plane spot, representing, respectively, 30°, 60°, and 75°.(e) Type 2 focal plane spot size. (f) The type 2 micro-lens has a long focal length effect at 30°,60°,and 75°.
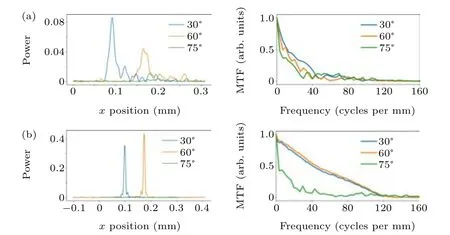
Fig.4. Focal plane spot distribution. (a)When light is obliquely incident on a type 1 lens it produces MTF.(b)When light is obliquely incident on a type 2 lens it produces MTF.
3. Discussion
Highly refractive silicon material is adopted for the design of the structural unit. This kind of highly refractive material can better confine light in the structure and weaken the mutual coupling between the structural units. In addition, a flexible 2πphase change can be provided. However, there is a problem of low efficiency in a micro-lens based on highly refractive materials. Part of the light will be lost due to the total reflection of the substrate. Most of the light is reflected and cannot be combined with the structural unit.
Table 1 summarizes the phases of the structural unit as a function of the cylinder diameter under different periods. The empirical function is helpful when optimizing micro-lenses.We have successfully designed two types of high-numerical aperture micro-lenses using Eq. (1). Both have their unique advantages, but type 2 micro-lenses are somewhat superior.A type 2 micro-lens, which relies on only a single lens, can achieve the effect of long-wave infrared wide-angle imaging(FOV>60°),and the FOV of this lens is only limited by the numerical aperture. In particular, its large focal depth can be used not only for achromatic imaging lenses but also for laser cutting. In addition, the focal plane spot maintains a good diffraction limit under wide-angle conditions.
In a word, through the design of empirical functions the simulation time is greatly shortened and the phase design can be worked out more easily. This method will be useful for future engineering applications.
4. Conclusion
In this paper the design of long-wave infrared wide-angle metalenses was studied. First, we looked at the design of the structural unit. We found that the phase function of the structural unit and the size of the structure can be used to predict the fitting function. Next,to verify the universality of this empirical function, a hyperbolic lens and a quadratic lens were designed. These two types of lenses were well focused under paraxial incidence. We observed spherical aberration in the quadratic lens. Simulations for a multi-angle lens were realized. Although the effect of the quadratic lens in paraxial optics is no better, it is excellent in wide-angle imaging and can achieve a wide-angle imaging effect of 120°(0.4@60 line pairs/mm)and maintain a good MTF value under multi-angle conditions. The empirical function studied in this paper can be used to optimize the superatom itself to provide a direction. Secondly, the quadratic lens has good performance and the unprocessability of traditional optics. The performance of the quadratic lens itself is good enough for wide-angle performance,but the quadratic lens can be used to design the second layer of a double-layer metasurface. By designing a different metasurface from the first layer, the spherical aberration that appears in the paraxial optics can be largely eliminated.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant No. 61875087) and Innovation and Development Foundation of China Academy of Engineering Physics(Grant No.CX20200021).
- Chinese Physics B的其它文章
- Solutions of novel soliton molecules and their interactions of(2+1)-dimensional potential Boiti–Leon–Manna–Pempinelli equation
- Charge density wave states in phase-engineered monolayer VTe2
- High-pressure study of topological semimetals XCd2Sb2(X =Eu and Yb)
- Direct visualization of structural defects in 2D semiconductors
- Switchable down-,up-and dual-chirped microwave waveform generation with improved time–bandwidth product based on polarization modulation and phase encoding
- Machine learning potential aided structure search for low-lying candidates of Au clusters

