池黃高鐵三塔矮塔斜拉橋施工控制參數研究

王 強 陸小雨

(1.皖贛鐵路安徽有限責任公司 安徽合肥 230000；2.中鐵上海設計院集團有限公司 上海 200070)

1 引言

矮塔斜拉橋以其橋塔高度低、主梁高度高的特點與常規斜拉橋區別開來，主梁為主要受力構件，拉索可視為體外預應力束對主梁進行加勁，因此學界又稱其為部分斜拉橋[1]。隨著中國鐵路網的快速建設，這一橋型在主跨150～300 m的橋式方案中具有較大的競爭力，受到了橋梁設計師的普遍青睞[2]。

由于實際施工過程與設計假定的施工步驟和荷載會有所差別，這就需要在施工過程中，通過施工控制對結構參數誤差進行修正，讓橋梁盡量能達到設計的合理成橋狀態[3]。為實現這一目標，需要對可能導致橋梁偏離設計理想狀態的各類因素進行研究，分析成橋狀態下結構內力和變形對各類參數的敏感性[4]。

隨著矮塔斜拉橋在近年來的推廣應用，雙塔矮塔斜拉橋的施工控制已有較多的研究成果，而針對多塔矮塔斜拉橋的研究還不夠充分[5]。因此，有必要針對多塔矮塔斜拉橋的施工控制進行研究。

本文以新建池黃高鐵三塔六跨矮塔斜拉橋為工程背景，選取主梁自重、主梁剛度、拉索初張拉力、拉索二次張拉次序、合龍溫度等參數，計算分析以上參數對橋梁力學性能的影響，為施工控制提供可靠的技術依據，為保證最終能達到合理成橋狀態提供有效的支撐[6]。

2 工程背景

池黃高鐵太平湖特大橋主橋為三塔六跨矮塔斜拉橋，結構體系為邊塔梁固結—中塔剛構的組合體系[7]，主橋長度為789.7 m(含支座中心線到梁端0.85 m)，橋跨布置為(48＋118＋2×228＋118＋48)m。主梁采用單箱雙室直腹板截面，梁高為6.0～12.0 m。橋塔采用雙柱式矩形截面，有效塔高均為35 m，單個橋塔設9對斜拉索。

主橋橋型布置如圖1所示，橋跨編號從小里程到大里程依次為A跨～F跨，橋墩位置分別為③號墩～⑨號墩，拉索編號分別為 A9→A1、B1→B9、C9→C1、C1→C9、B9→B1、A1→A9。

圖1 橋型布置(單位:m)

3 有限元模型的建立

采用有限元分析軟件Midas Civil 2021建立斜拉橋的計算模型，全橋共劃分為937個節點，889個單元。其中，塔、梁、墩臺和樁基均采用梁單元模擬，拉索采用桁架單元模擬，樁基底部采用固結約束，其他橋墩采用節點支承進行模擬。

0號塊和邊跨現澆段采用支架現澆法施工，其余梁段采用掛籃懸臂澆筑，施工過程共劃分為57個施工階段，其中懸臂梁段的施工內容主要包括掛籃移動、梁段澆筑、預應力筋的安裝與張拉、斜拉索的安裝與張拉。橋梁有限元模型如圖2所示。

圖2 橋梁空間有限元模型

4 施工控制參數研究

4.1 研究方法

根據施工經驗，選取主梁自重、主梁剛度、拉索初張拉力、拉索二次張拉次序和合龍溫度五個參數進行研究，以設計參數作為基準狀態，通過改變某個參數的取值，同時保持其余參數不變，對橋梁的力學性能進行分析。由于矮塔斜拉橋的豎向剛度主要由主梁和拉索提供，橋塔的作用僅為提供斜拉索的轉向[8]，因此選取成橋狀態下主梁線形、主梁應力、拉索內力為施工控制的重要目標，最后對各參數對控制目標的影響程度進行排序[9]，見表1。

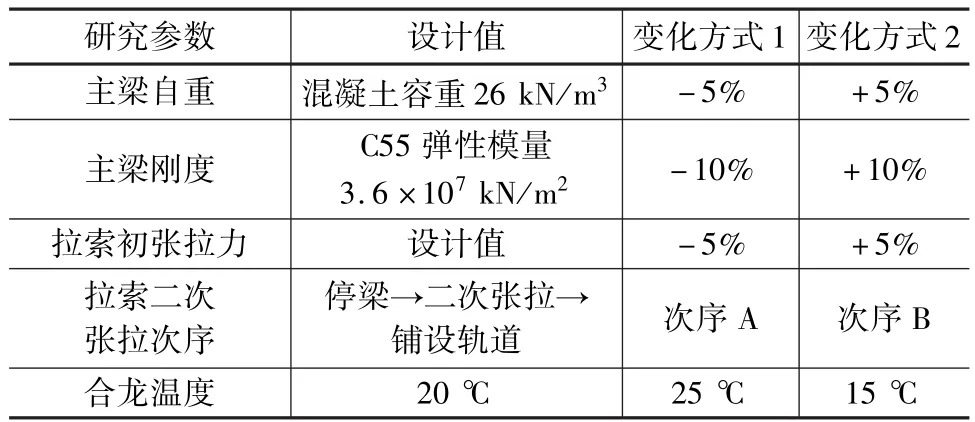
表1 主要研究參數及變化方式

4.2 主梁自重

由于施工現場的混凝土容重與設計采用值不可能完全一致，故通過改變主梁混凝土容重實現主梁自重的變化。以主梁混凝土容重設計值為基準狀態，按幅度為±5%對混凝土容重進行變化，計算分析成橋狀態下主梁線形、主梁上下緣應力和拉索內力的變化值，計算結果如圖3所示。圖中橫坐標表示主梁順橋向的位置，起點為邊支點，由于本橋為對稱結構，故圖中僅示半橋的結果，下同。

由圖3可知，當主梁自重變化5%時，主梁豎向下撓值最大增加15.4 mm；主梁上、下緣壓應力最大增加值分別為1.1 MPa和1.07 MPa，對應增幅分別為8.9%和14.7%；拉索內力最大增加26.5 kN，增幅為0.3%。主梁自重變化對3/8跨處豎向撓度和中支點主梁上、下緣應力影響最大；長索受到主梁自重變化的影響相比短索要大。

綜上所述，主梁自重變化對橋梁的力學性能影響不可忽略，由于高鐵行車對主梁線形較為敏感[10]，因此在施工過程中，需根據現場混凝土的實際容重對計算模型進行修改，對主梁預拱度值進行修正，保證橋梁能達到設計成橋線形。

4.3 主梁剛度

由于現場的混凝土彈性模量與設計值不可能完全一致，故主梁剛度的變化通過改變混凝土彈性模量來實現[11]。以主梁C55混凝土彈模設計值為基準，按幅度為±10%對混凝土彈模進行變化，保持其他參數不變，計算結果如圖4所示。

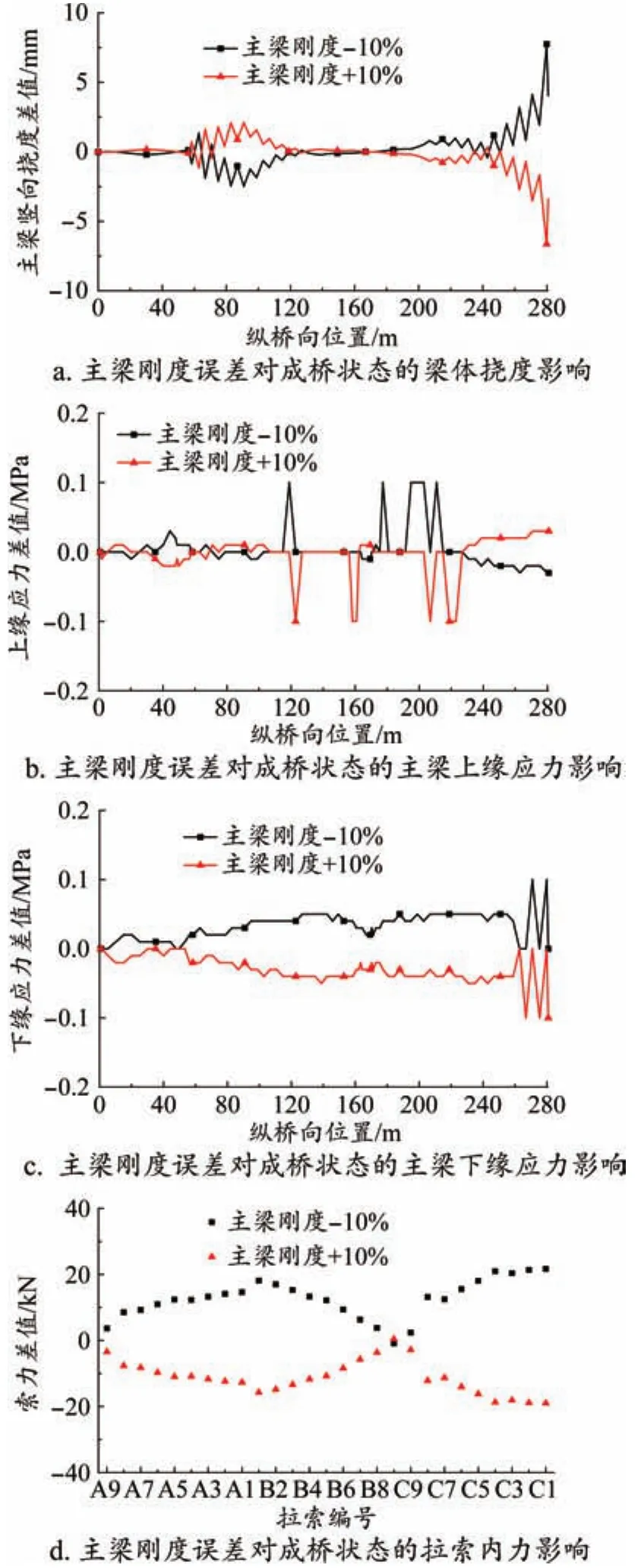
圖4 主梁剛度誤差對結構內力、變形的影響規律

由圖4可知，主梁彈性模量變化10%，主梁豎向撓度最大增加7.8 mm；主梁上、下緣壓應力最大增加值均為0.1 MPa，增幅分別為0.9%和1.0%；成橋拉索內力最大增加21.7 kN，增幅為0.4%。

因此，主梁剛度變化對成橋狀態的線形影響較大，而對主梁應力和拉索內力的影響可忽略不計。由于高速鐵路對橋梁線形要求高，因此在施工過程中仍需保證混凝土彈性模量與設計值盡量一致，若有差別時，應及時調整計算模型，對預拱度進行修正。

4.4 拉索初張拉力

根據施工經驗，斜拉索在張拉后，其內力很難與設計值完全一致[12]，以拉索初張拉力的設計值為基準，按幅度為±5%對其進行變化，計算結果如圖5所示。

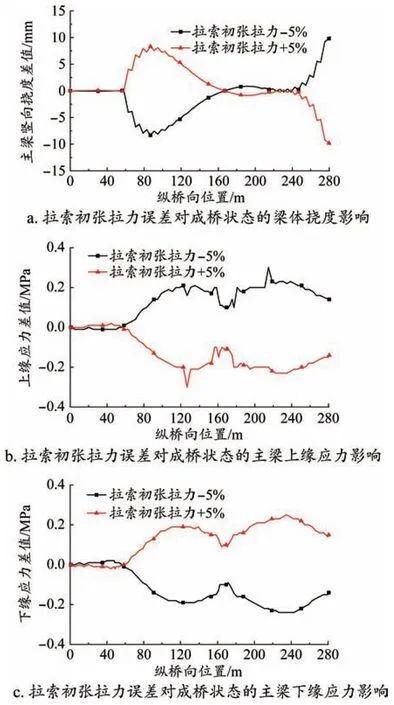
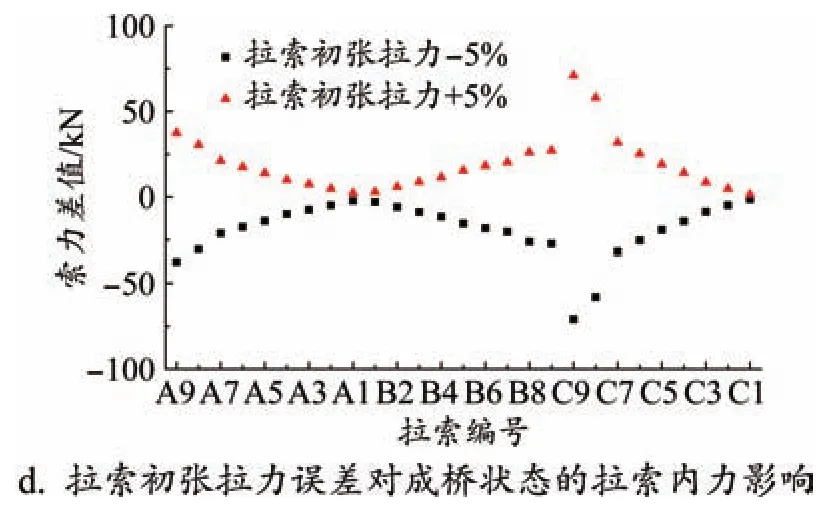
圖5 拉索初張拉力誤差對結構內力、變形的影響規律

由圖5可知，拉索初張拉力變化5%，主梁豎向撓度最大增加10.12 mm；主梁上、下緣壓應力最大增加值分別為0.23 MPa和0.24 MPa，增幅分別為2.8%和3.1%；成橋拉索內力最大增加70.9 kN，增幅為1.0%。

因此，拉索初張拉力變化對成橋狀態的線形影響較大，對主梁應力和拉索內力的影響較小。由于斜拉索在鋪軌前會進行拉索的二次張拉，因此初張拉力變化時，成橋階段的拉索內力變化很小。

4.5 拉索二次張拉次序

設計指定的施工次序為:停梁60 d→斜拉索二次張拉→鋪設軌道。以此為基準狀態，考慮以下2種張拉次序:(1)次序A，拉索二次張拉→停梁60 d→鋪設軌道；(2)次序B，停梁60 d→鋪設軌道→拉索二次張拉。計算結果如圖6所示。

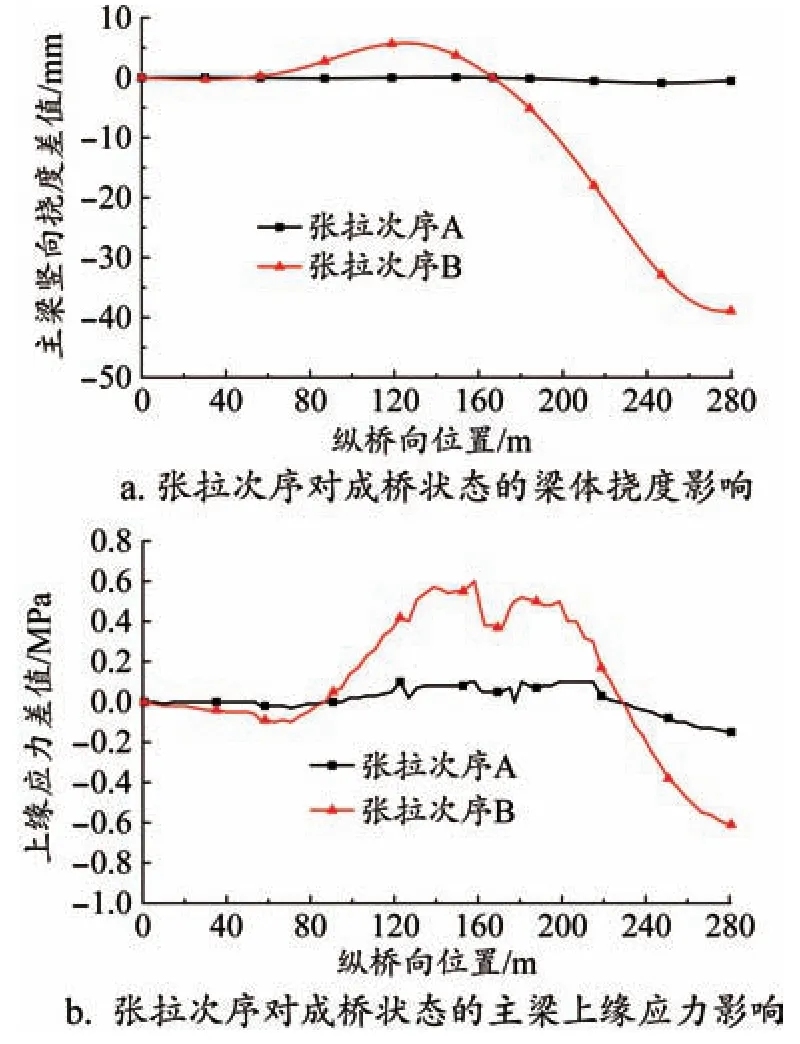
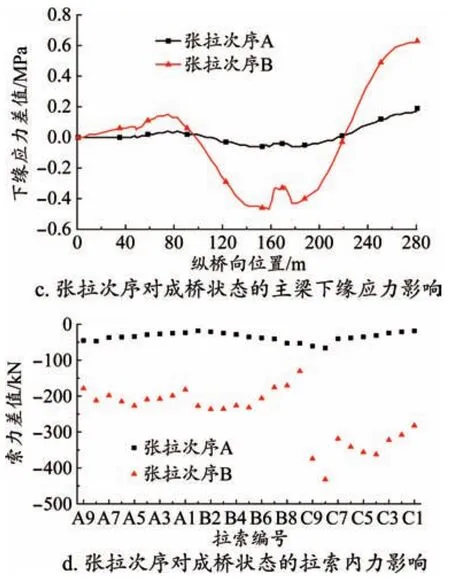
圖6 張拉次序對結構內力、變形的影響規律

由圖6可知，張拉次序A相比于張拉次序B對結構的內力和變形影響較小。當采用張拉次序B時，主梁豎向撓度最大下撓39.0 mm；主梁上、下緣壓應力最大增加0.6 MPa和0.47 MPa，增幅分別為9.5%和8.2%；成橋拉索內力最大增加432.0 kN，增幅為5.8%。

因此，采用張拉次序B對施工控制重要目標的影響均較大，因此實際施工時，二次張拉應按設計指定次序進行，以確保橋梁達到理想成橋狀態。

4.6 合龍溫度

設計時假定合龍溫度為20℃，由于實際工期未必能滿足設計要求，本文按幅度為±5℃對合龍溫度進行變化，計算結果如圖7所示。

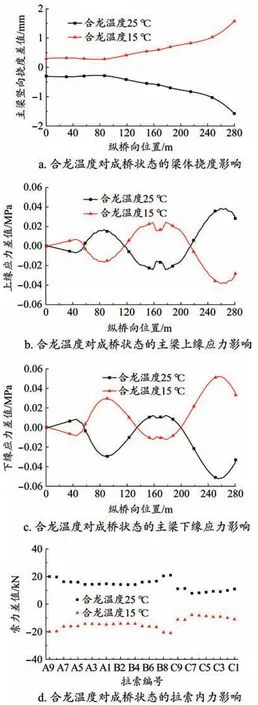
圖7 合龍溫度對結構內力、變形的影響規律

由圖7可知，合龍溫度變化5℃時，主梁豎向撓度最大增加1.6 mm，主梁上緣壓應力最大增加0.04 MPa，增幅為0.6%；主梁下緣壓應力最大增加0.05 MPa，增幅為0.5%；成橋索力最大增加21.0 kN，增幅為0.3%。

綜上可知，合龍溫度變化對施工控制的重要目標結果影響均較小。由于結構采用了邊塔梁固結—中塔剛構的組合體系，使得結構對溫度的敏感性相比于全剛構體系大大降低[13]。

4.7 小結

(1)主梁線形敏感性參數研究

對影響主梁線形的各個參數的敏感性進行排序，如表2所示。表中參數對施工控制重要指標的影響越大，其編號越小，下同。

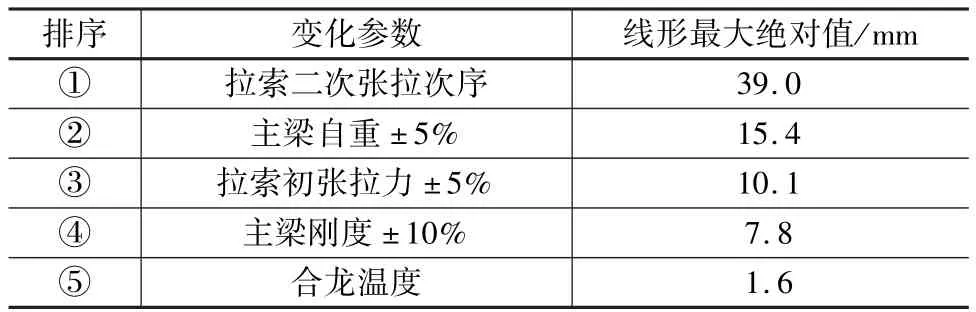
表2 主梁線形敏感性參數研究結果匯總

由表2可知，拉索二次張拉次序、主梁自重、拉索初張拉力和主梁剛度是主梁線形的主要敏感性參數，合龍溫度為次要敏感性參數。

(2)主梁應力敏感性參數研究

對影響主梁應力的各個參數的敏感性進行排序，如表3所示。

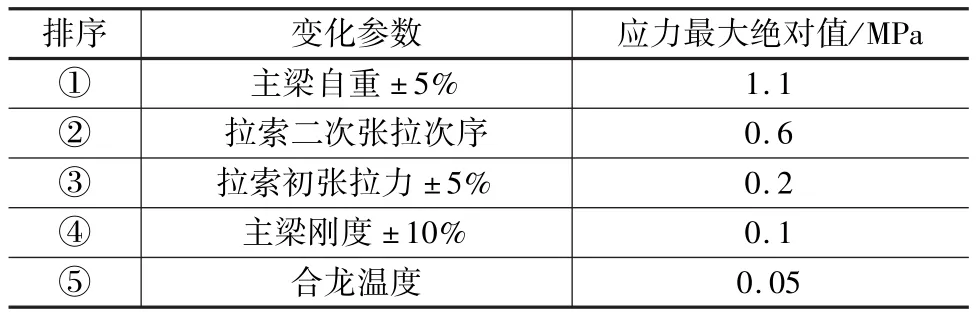
表3 主梁應力敏感性參數研究結果匯總

由表3可知，主梁自重、拉索二次張拉次序是主梁應力的主要敏感性參數，其余均為次要敏感性參數。

(3)拉索內力敏感性參數研究

對影響拉索內力的各個參數的敏感性進行排序，如表4所示。

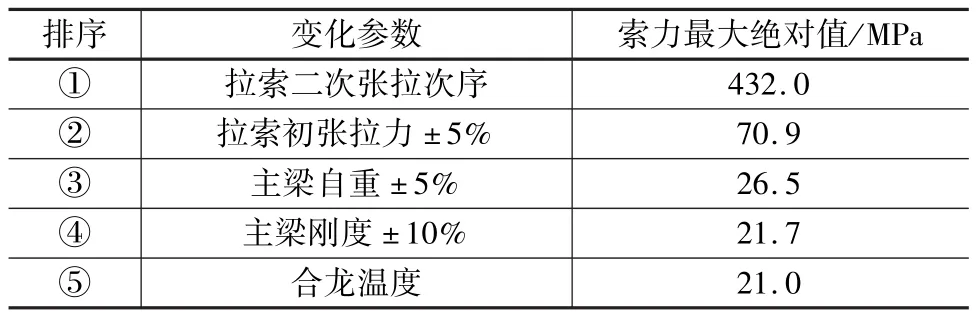
表4 拉索內力參數敏感性參數研究結果匯總

由表4可知，拉索二次張拉次序和拉索初張拉力是拉索內力的主要敏感性因素，其他因素的變化對主梁線形影響很小。

5 結語

本文對池黃高鐵(48＋118＋2×228＋118＋48)m多塔矮塔斜拉橋的施工控制參數進行研究，得出結論如下:

(1)由于高速鐵路行車對主梁線形較為敏感，主梁自重和剛度、拉索初張拉力和二次張拉次序對主梁線形影響均較大，施工過程中應對以上參數進行嚴格控制，以保證橋梁能達到設計線形。

(2)主梁應力受主梁自重的變化影響較大，由于矮塔斜拉橋以主梁受力為主，主梁內力較大，因此需嚴格控制主梁自重這一參數以保證主梁內力能達到設計指定狀態。

(3)拉索二次張拉次序和拉索初張拉力是拉索內力的主要敏感性參數，施工過程中應對張拉后的拉索索力進行復測，對索力偏差較大的拉索應及時調整，確保索力與設計值一致。

(4)本橋采用邊塔梁固結—中塔剛構的組合體系，該體系對溫度的敏感性較低，在季節溫度變化結構的受力性能變化較小。