可燃冰與油氣雙儲層模型的海洋可控源電磁響應特征模擬分析

高 妍 馬 超*③ 張向宇

(①廣州海洋地質調查局，廣東廣州 511458；②南方海洋科學與工程廣東省實驗室(廣州)，廣東廣州 511458；③天然氣水合物勘查開發國家工程研究中心，廣東廣州 511458)

0 引言

海洋可控源電磁(MCSEM)法是有效探測海底電阻率異常體的重要方法之一，在海洋地質調查(海洋底構造、洋脊擴張、火山運動等)、海底資源(油氣、水合物、地下水、多金屬硫化物等)探測等諸多領域得到了成功應用[1-7]。該方法的優勢在于：①相較于海洋地震方法，勘探成本低；②電磁響應對異常體的電阻率差異靈敏度高，可有效降低油藏勘探和開發的風險；③是地震勘探方法的有效補充，如在天然水合物調查中，對于地震方法無法識別的天然水合物頂界，電磁法可以有效識別。淺海的可燃冰儲層具有高電阻率特性，利用MCSEM勘探不僅可以估算可燃冰的飽和度分布，也可與地震勘探結合，優勢互補，顯著降低鉆探風險、提高鉆探成功率[8]。中國的MCSEM勘探始于2016年在瓊東南海域利用自主研制的海底電磁接收機開展的可燃冰探測試驗[9]。

MCSEM的正演是反演以及實際應用研究的基礎。由于海底地層的電性結構可能非常復雜[10]，因此開發一個適用于MCSEM復雜三維模型的穩定且有效的正演算法至關重要。本文提出一種基于預條件迭代求解的頻率域矢量有限元電磁模擬方法，可高效地進行復雜海底地形條件下的MCSM模型正演模擬。

MCSEM正演模擬的數值方法主要包括有限差分法、有限元方法、積分方程法、多網格法[11]等，這些方法各有優、缺點。有限元方法構造的源項采用單元積分方法，相比有限差分的加權平均方法更精確，因此有限元方法的求解精度理論上更高，并且更適用于復雜地質模型的構建。已證明有限元方法是一個適用于地球物理問題中任何復雜的二維或三維結構的數值分析的有效工具，其中矢量有限元方法因其算法穩定、求解效率高且適合于復雜幾何形狀模型的模擬，一直是電磁模型領域的研究熱點[12-15]。矢量有限元(比如六面體單元)方法中，單元內的電場之間具有更緊密的耦合關系，且插值函數具有嚴格的無散性。Mitsuhata等[16]提出了一種基于矢量有限元的大地電磁建模算法。Schwarzbach等[17]基于線性高階矢量有限元，利用四面體單元離散對MCSEM數據進行建模，精確地再現了真實海洋深水模型。

三維模型模擬中，曲面的離散可使用普通網格、六面體單元或四面體單元。對于三維矢量有限元模擬，四面體單元具有結構可任意離散化的特點[18-19]。比較而言，基于六面體單元的矢量有限元則更易實現結構化網格[20]、模型加密，具有正反演網格操作簡單[21]等優勢，集合了有限差分易于離散和矢量有限元對復雜模型適應性強的優勢，得到了廣泛的應用[22-24]。Nam等[25]利用規則六面體單元的矢量有限元建立了大地電磁三維模型，研究了海洋火山地形與水深對不同頻段大地電磁數據的影響，并進行了數值分析。Kordy等[26]將直接求解法應用于不規則六面體單元的矢量有限元方法，并進行了散度校正，結果證明該方法可用于準確求解復雜地形的電磁響應。

在有限元求解框架下搭載穩定、高效的矩陣可顯著提高求解效率。迭代方法是計算有限元稀疏矩陣的重要方法，其優點是計算量小、對計算機的存儲要求低[13,27]。預條件方法在矩陣迭代求解中具有非常重要的作用，最重要的一種預條件方法是對矩陣的不完全分解，常見的是不完全LU(ILU)分解。考慮矩陣對稱情形，當矩陣正定性較強時，不完全Cholesky分解[28]也是非常有效的預條件手段。Um等[29]提出電磁場散射公式的有效ILU預條件的有限元迭代策略，并在多源、多頻、多模型等不同條件下全方位地對幾種預條件方法的效率進行了評價，提出正確選擇預條件方法可以大大減少復雜海底模型的計算量和計算時間。

針對復雜電性結構海底地層模型，本文提出一種基于預條件迭代求解的頻率域矢量有限元電磁正演模擬方法，基于ILU分解的預條件方法，提高了迭代求解效率。建立層狀海洋電磁模型，通過模擬電場響應，并與解析解進行對比，驗證了本文算法的有效性。基于結構化任意六面體單元建立了中國南海某海域真實地電框架模型，并針對不同構造礦藏儲層特征，分別建立了深埋藏油氣儲層模型、可燃冰礦體模型及復雜基底地質模型，應用前述方法計算電場響應，對不同激發、接收模式下的MCSEM響應特征進行分析，并進一步總結出適宜的探測參數設置條件。

1 方法原理

1.1 控制方程

地球物理勘探領域中常用到低頻電磁場需滿足的宏觀電動力方程，即Maxwell方程組。在穩場近似下，可忽略位移電流。假設時間諧變因子為eiωt，頻率域Maxwell方程組可表示為

(1)

式中：E表示空間電場；H表示空間磁場；ω表示圓頻率；磁導率μ=μtμ0=4π×10-7H/m，其中μt和μ0分別表示相對磁導率和真空中的磁導率；J和M分別表示電流密度和磁流密度；q表示體電荷密度；σ為介質電導率；B表示磁感應強度；D表示電位移矢量。

由于背景場在源附近急劇變化，用有限元法直接求解總場時，在邊界處可采用稀疏網格，在場源附近則需采用精細網格。為了提高計算效率，可以采用求解異常場的方法求解總場。以電場E為例，首先將其分解為異常場Ea與背景場Eb之和，即E=Ea+Eb，Eb可以通過求解全空間或半空間的解析解得到，這樣可得到基于電場異常場Ea的二階偏微分方程

?×(μ-1?×Ea)+iωσEa=-iω(σ-σb)Eb

(2)

式中上標“b”代表背景。對使用偶極子源進行激發的情形，采用異常場方法構造的源項更加平滑，有利于數值求解。背景場為均勻全空間或者層狀介質的電場分布，可由快速漢克爾變換方法求得[30]。

為了表示的簡潔性，后文中用E代表電場異常場Ea。假設求解目標在三維長方體域Ω內滿足狄利克雷邊界條件的解，式(2)可以表示為算子的簡單形式

AE+iωσE=b

(3)

式中：A=?×μ-1?×；b=-iω(σ-σb)Eb。數值求解得到電場E后，可根據法拉第定律直接求解磁場

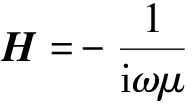
(4)

1.2 頻率域有限元離散

本文使用矢量有限元方法求解式(3)，將矢量形函數定義在單元的邊上，然后通過插值表示單元中各點的場值。這里采用六面體單元，六面體單元中節點和電/磁場的位置如圖1所示。

圖1 六面長方體單元中節點和電/磁場位置示意圖

定義單元e沿x、y和z方向的邊長分別為Δxe、Δye和Δze，單元內任一點的電場分量可以表示為

(5)

矢量基函數在單元邊界也是連續的，因此基于矢量有限元的公式也適用于無源條件下的電磁場模擬。采用Galerkin方法[30]，設殘差函數(式(2))的弱形式為零

f(E)=?ΩNj·[?×(μ-1?×E)+

iωσE+iω(σ-σb)Eb]dV=0

(6)

式中Nj表示第j個插值函數。基于矢量恒等式和第一矢量格林定理，對于單元e，式(6)可寫成

iω(σ-σb)MeEb]=0

(7)

式中：ne表示與單元e插值相關的單元個數；Ge和Me分別為單元剛度矩陣和單元質量矩陣，其表達式為

(8)

將單元剛度矩陣Ge整理到總剛度矩陣G即可得到最后的線性方程組，借助相應的矩陣求解器，即可直接求解三維電場E的分布。

通常情況下，僅僅使用長方體網格無法精確模擬復雜地球物理模型[31]。在海洋電磁模擬中，電磁響應受地形起伏的影響很明顯，粗糙的網格剖分會嚴重影響模擬結果對目標的分辨率。因此，基于不規則六面體單元的有限元方法在結果驗證和數據補充方面具有重要的意義。可采用坐標變換將基于xyz坐標系的任意六面體單元(圖2a)映射為基于ξηζ坐標系的長方體單元(圖2b)

圖2 六面體單元從xyz坐標系(a)映射到ξηζ坐標系(b)

(9)

其中

(10)

為了建立平行于ξ軸的四個邊的形函數，首先定義ξ為常數的面。由于該面垂直于ξ軸，在面上?ξ只有法向分量，這樣通過?ξ定義的形函數只在平行于ξ軸的邊上才有非零切向分量。根據式(10)建立六面體單元的矢量形函數

(11)

矢量形函數滿足插值電場在切向分量上的連續性，因而可有效壓制偽解的產生。對六面體單元e，與式(8)對應的形式為

(12)

式中J為Jacobian矩陣。

將式(9)和式(10)代入式(12)可得

(13)

六面體單元的矢量形函數式(11)的旋度為

(14)

確定了形函數及形函數的旋度后，式(13)可用三維數值積分的方法(如八點高斯積分)進行求解[20]，得到

(15)

式中：ξi、ηj和ζk分別為高斯積分點；Wi、Wj和Wk分別為加權系數。

1.3 基于ILU分解的預條件迭代方法

ILU分解預條件方法給大型稀疏方程組的求解帶來很多新的思路和靈活選擇。比如多重網格方法，在規則網格的假設下可進行完美的多級求解[30]，但對非規則網格問題往往不能達到理想效果。利用ILU以及改進ILU(MILU)可實現有效的多級求解。對系數矩陣C，定義最簡單的ILU分解為

C=LU+δ

(16)

式中：δ表示殘差；L和U分別代表下三角和上三角矩陣，且與矩陣C的上三角和下三角部分具有完全相同的稀疏性，即非零元素的結構一致，這種情況被稱為ILU0分解。ILU0分解可通過按行進行的高斯消元法實現，并舍棄所有零元素對應位置的元素。基于這樣的定義，ILU0分解對矩陣的分解精度不高，在一定程度上甚至會破壞對角線元素的占優性。

本文提出一種Jacobian+ILU0的預條件方法，具體分為兩步：首先，將系數矩陣C分成上三角和下三角部分，并把上三角部分賦給U；然后，用ILU0分解計算L，L的對角線元素均為1。

2 數值算例

2.1 正演模擬算法有效性驗證

2.1.1 精度驗證

建立兩個MCSEM層狀模型，這兩個模型的區別在于異常層的厚度和深度不同，通過模擬這兩個模型的電磁響應分析本文求解方法的精度。

模型(圖3)包括海水層、海底地層、高阻異常層以及基底，兩個模型的區別在于高阻異常層的厚度(分別為100、650m)和深度(分別為2000、1200m)。假設水平電偶極子(HED)源沿x方向置于海底以上50m，源中心點的x坐標為0，以100A·m的電偶極矩發射方波電信號。接收器置于海底，測量x方向的電場Ex。下文針對非異常體和異常體區域分別對采用長方體網格和不規則網格情況下的電磁模擬精度進行對比。

(1)非異常體區域

對圖3a模型的z∈[-1km,1km]分別用長方體和不規則矩形網格進行劃分，結果見圖4a和圖4b。設背景電場響應振幅為Eb，解析解為Et，數值解為Es。根據下式計算電場模擬的相對誤差

圖3 高阻層不同厚度和深度的MCSEM模型

圖4 圖3a模型非異常體區域網格劃分方案

(17)

0.25Hz的電場分量Ex模擬結果見圖5。迭代過程中迭代殘差范數設定為1×10-6。可以看出，有限元分析結果與半解析解吻合較好，兩種網格的模擬結果相對誤差均小于4.0%，規則網格剖分和非規則網格剖分的模擬結果最大相對誤差分別為3.8%和2.9%。可見，非規則矩形網格劃分情況下的模擬精度略高，尤其是在收發距較大的情況下。

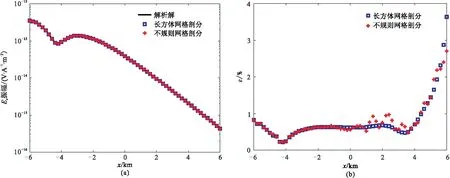
圖5 圖4兩種網格剖分的MCSEM模型電場響應Ex振幅(a)及相對誤差(b)

(2)異常體區域

對圖3b模型中的高阻異常層分別進行長方形網格和不規則矩形網格剖分(圖6)。0.25Hz時的Ex振幅模擬結果見圖7。可以看出，使用長方體網格和不規則矩形網格對高阻異常層進行剖分時，對應的模擬最大振幅相對誤差分別為3.7%和2.3%，可見整體上非規則矩形網格剖分情況下的模擬誤差更小。

圖6 圖3b模型中高阻異常層的長方體網格剖分(a)和不規則矩形網格剖分(b)

圖7 圖6兩種網格剖分的模型電場響應Ex振幅(a)及相對誤差(b)

2.1.2 預條件算法效率分析

利用前文提到的三種預條件方法(Jacobian預條件方法、ILU0預條件方法及ILU0 + Jacobian預條件方法)進行數值算例測試，以評估不同預條件方法的有效性和可行性。

建立兩種MCSEM模型進行預條件算法算例測試，即圖8模型(平坦海底地形)和圖9模型(崎嶇海底地形)。將HED源中點置于x=-6.0km、z=1.6km處進行激發，并用有限元方法正演計算電磁響應。對這兩個模型分別剖分為長方體網格和不規則四邊形網格。

本文采用擬最小殘差法(QMR)迭代求解，不同預條件方法下的迭代收斂曲線見圖10。可以看出：采用Jacobian預條件方法的迭代收斂效果最差，平坦海底模型(圖8)經過2000次迭代后的殘差范數為5.290×10-3，而崎嶇海底地形模型(圖9)經3000次迭代后的殘差范數為3.489×10-4；ILU0預條件方法較Jacobian預條件方法的迭代收斂效果略好，圖8模型經758次迭代后的殘差范數為9.931×10-6，而圖9模型經796次迭代后的殘差范數為9.996×10-6；采用Jacobian+ILU0預條件方法的迭代效果最優，圖8模型經498次迭代后的殘差范數為9.884×10-6，圖9模型經388次迭代后的殘差范數為9.761×10-6。

圖10 圖8模型(a)和圖9模型(b)不同預條件方法下的迭代收斂曲線

與其他兩種預條件方法相比，本文提出的Jacobian+ILU0預條件方法對圖8和圖9模型所需迭代次數更少，收斂更平滑，尤其對崎嶇海底地形模型的迭代表現出了較強的適用性。因此，Jacobian+ILU0預條件方法在MCSEM模型有限元正演模擬中表現出了較好的收斂性能，即便對崎嶇海底地形模型也表現出較好的模擬收斂效果。

圖8 平坦海底層狀MCSEM模型及網格剖分

圖9 崎嶇海底層狀MCSEM模型及網格剖分

2.2 MCSEM深水模型仿真模擬

受淺水域空氣波的影響，深水模型的異常體較淺水模型的異常體響應更明顯[32]，但前提是海底地形是平坦的。當海底地形崎嶇時，深水模型異常體的響應特征有待研究，為此，建立深水崎嶇海底模型進行仿真模擬。基于公開的中國南海某海域海底地形數據(圖11)，建立不同的三維儲層模型，進行MCSEM有限元仿真模擬。

圖11 中國南海某海域三維海底地形

2.2.1 考慮海底地形的油氣儲層模型

圖12所示三維儲層模型包含海底地形信息，油氣儲層為4km(x)×4km(y)×100m(z)的長方體，油藏頂面位于海平面以下3km處。HED源(Tx)沿x方向在-10～10km范圍內拖曳前行，距離海底的高度始終保持為50m。接收器(Rx)放置于海底，沿x方向均勻布設，測量-10～10km范圍內的水平電場Ex，源Tx與測線位于同一xOz平面[33]。

圖12 考慮海底地形的三維MCSEM儲層模型及網格剖分

圖13a為水平電場Ex振幅隨Tx-Rx偏移距(這里指Tx中點在海底的投影點與Rx的x坐標之差，后文簡稱收發距)的變化曲線，參考背景幅度為直線。可以看出，在收發距較小(1～3km)的情況下，異常體的電場分量Ex振幅較大，即異常體所在的平面位置附近Ex振幅出現正異常，但異常幅值總體不大，局部被地形影響抵消。可見收發距在3km以內時，地形對水平電場的影響較為明顯，即使在儲層埋藏較淺的情形下也難以明確判斷儲層范圍。隨著收發距的增加(4～6km)，異常體響應逐漸變得明顯，由于地形對電場振幅的影響較小，曲線較為光滑。因此，對于該模型，在地形變化不太劇烈情況下進行儲層識別的適宜收發距是4～6km。當收發距進一步增大(7～8km)時，異常體響應減弱，曲線劇烈震蕩，這是地形與異常體共同作用的結果，在這個收發距范圍內，僅通過Ex振幅曲線已經無法有效識別儲層。

以1500m水深的均勻海底地層模型(含海底地形)的電場響應作為背景場，計算Ex振幅與背景場的比值，得到歸一化曲線(圖13b)。可見歸一化曲線與圖13a振幅曲線的變化趨勢一致，但根據歸一化曲線可較直觀地判斷儲層的平面分布范圍。整體而言，收發距較小時的Ex振幅歸一化曲線，尤其是2km時，曲線異常范圍與高阻油藏的水平范圍基本吻合。隨著收發距逐步增大，歸一化振幅隨之增大，歸一化曲線異常邊界逐漸模糊。當收發距大于6km時，歸一化振幅開始變小，同時地形的影響開始增大，油藏的響應逐漸被淹沒。

與圖13對應的Ex相位及相位差見圖14。由圖可見，相位曲線(圖14a)與振幅曲線(圖13a)特征基本一致。需指出的是，相位對地形起伏不敏感，尤其是在儲層響應最明顯的4～6km收發距范圍內，相位曲線非常平滑。當收發距增大到7～8km時，在相位曲線上可以同時觀察到明顯的儲層(低頻信號)和地形(高頻信號)響應疊加在一起形成的鋸齒狀響應。與歸一化Ex振幅(圖13b)相比，相位差曲線(圖14b)上出現相同特征所對應的收發距大于1km，且曲線更平滑。

圖13 圖12模型模擬Ex振幅(a)及歸一化振幅(b)曲線

圖14 圖12模型模擬Ex相位(a)及相位差(b)

2.2.2 考慮海底地形和近海底可燃冰分布的油氣儲層模型

中國南海海域具有豐富的可燃冰資源。可燃冰形成于低溫高壓環境，因此通常分布于近海底區域，在可燃冰穩定區域之下常常會有高飽和的伴生天然氣，造成近海底地層電阻率明顯增大。可燃冰在海底一般是非均勻分布的。基于圖12所示模型，在海底增加四個不連續分布的可燃冰礦體，礦體沿y方向的延伸范圍與儲層范圍一致(4km)，建立考慮地形和近海底可燃冰分布的油氣儲層模型(圖15)，網格剖分方案同圖12。

圖15 考慮海底地形和近海底可燃冰分布的三維油氣儲層模型及網格剖分

應用本文正演方法得到不同收發距下縱測線水平電場Ex振幅及歸一化振幅曲線(圖16)。與僅考慮海底地形的情況(圖12)相比，含可燃冰礦體模型的歸一化振幅的最大值增大約2倍，曲線扭曲嚴重，僅收發距較小時所對應的歸一化振幅曲線可較清楚地分辨可燃冰礦體的分布范圍(圖16b中虛線橢圓所示)，但儲層分布范圍難以判斷。據圖16還可以看出，含海底地形和可燃冰礦體的油藏模型電場響應非常復雜，可燃冰礦體的電場響應與海底地形耦合所產生的響應疊合在一起，使儲層響應難以識別。可燃冰礦體分布的非均質性越強，響應越復雜。特別地，當可燃冰礦體與油氣儲層的水平分布范圍大致相同時，二者的響應會疊加在一起，對目標儲層的識別則愈加困難。進一步地，若目標儲層水平分布范圍較小，要對其進行識別就更難以實現。

圖17所示為電場分量Ex相位及相位差曲線。從圖17a所示相位曲線可以看出，可燃冰礦體引起的異常范圍隨著收發距的增大逐漸減小，當收發距達到6km時已無法觀察到可燃冰礦體引起的明顯擾動。收發距逐漸增大，可燃冰礦體的電磁響應與儲層響應逐步發生疊合，因此異常極大值點明顯漸漸向右偏移。從圖17b所示相位差曲線可以看出，收發距為1km時，可清楚識別可燃冰礦體的分布范圍，但可燃冰礦體和儲層響應難以區分；收發距增加到2km時，較1km收發距時相位差增大，但可燃冰礦體和儲層響應仍難以區分；當收發距逐漸增大至6km時，可燃冰礦體的響應逐步減弱，相位差曲線的中心點逐漸向儲層中心移動，可較準確地判斷儲層的平面位置，這與圖16b揭示的特征一致。因此，若存在可燃冰礦體時，在保證信噪比的前提下，為更好地識別油氣藏，應盡量采用較大的收發距。

圖16 圖15模型模擬Ex振幅(a)及歸一化振幅(b)曲線

圖17 圖15模型模擬Ex相位(a)及相位差(b)

2.2.3 考慮海底地形和基底地層起伏的復雜地質模型

利用電磁數據可較準確地解釋電性異常體的橫向(平面)分布范圍，其缺點是縱向分辨率較低，難以精確重建地層模型，而地震勘探的優點在于縱向分辨率高，與電磁方法形成互補關系。因而，開展高精度電磁勘探時，結合地震解釋成果對電性層位進行深度標定，是提高電磁勘探效果的重要手段。利用地震資料的處理和解釋成果能較精確地確定海底標志層，結合電磁法對電性異常體的平面分布解釋成果，可建立區域地球物理框架，建立相應的地電模型，為高精度電磁勘探提供基礎數據。

根據中國海南某海域地震解釋成果和電磁資料，建立一個三層的地球物理框架，框架包括海底地形及海底地層。基于此框架，分別建立四個模型M0、M1、M2和M3(圖18)：M0只考慮海底地形和基底；M1考慮海底地形、次高阻層和基底；M2綜合考慮海底地形、次高阻層、基底及高阻油氣儲層；M3考慮海底地形、基底和高阻油氣儲層。

圖18 基于海南某海域地球物理框架建立的電阻率模型

采用2.2.1節的激發、接收參數，這里僅分析源位于-5km時的情形。圖19是這四個模型的模擬Ex振幅剖面，頻率為0.25Hz。從圖19b和圖19c可以看出，雖然模型中存在厚度較大的次高阻層，但由于與背景電阻率差異(2倍)較小，Ex振幅曲線并無明顯異常。從圖19d可以看出，雖然模型M3中油氣儲層的厚度和分布范圍都比模型M1和M2中的次高阻體小得多，但卻引起了較明顯的電場變化，這是由于儲層與圍巖的電阻率差較大(50倍)。

圖19 CSEM模型模擬Ex振幅剖面

以模型M0的模擬數據為背景場，對模型M1、M2、M3的Ex振幅(圖20a)進行歸一化，結果見圖20b。從圖20b所示歸一化曲線上可以看出，收發距為2km曲線上次高阻體的特征比較明顯(圖20b中紅色虛線框所示)，而油氣儲層的響應(圖20b中的綠色虛線框所示)則在收發距大于5km才可看出明顯異常。這說明不同埋藏深度的電阻率異常體所對應的電磁響應會體現在不同收發距的電場數據中。同時還可以看出，在收發距大于9km(即對應坐標4km位置)時，油氣儲層的響應依然很明顯，但振幅較小，這樣的有用信號在實際勘探中容易被噪聲淹沒。

圖20 模型M0、M1、M2和M3的模擬Ex振幅(a)及歸一化振幅(b)曲線

圖21是模型M0、M1、M2和M3正演電場分量Ex的相位及相位差曲線，其中背景響應采用模型M0的相位數據。

由圖21可見，相位參數可更直觀地顯示不同模型電場響應的差異。根據圖21a，四條曲線整體上可分成兩簇，一簇是模型M0和模型M3響應曲線，另一簇是模型M1和模型M2響應曲線。這兩簇曲線在收發距為-2.5km處出現分歧，這與淺部次高阻層的位置有關；隨著收發距逐漸增至約5km時，兩簇曲線中的兩支曲線均發生分離，相位差逐漸增大，這與油氣儲層的平面分布范圍有關；隨著收發距進一步增大，四條曲線最終在收發距為10km處趨于一致，表明此處已無法觀測到淺部次高阻體或深部高阻油藏引起的電磁異常。圖21b相位差曲線也顯示出與圖21a類似的特征，其中模型M2和M3中油藏產生的相位差分別約為60°和30°，而淺部異常體產生的相位差則很小。

圖21 模型M0、M1、M2和M3模擬Ex相位(a)及相位差(b)曲線

3 結論

基于預條件迭代求解的頻率域矢量有限元模擬，本文實現了結構化任意六面體單元的三維海洋可控源電磁響應模擬，通過與層狀模型的解析解對比驗證了算法的正確性和有效性。本文提出了簡化的ILU0預條件方法，有效提高了迭代求解的效率，收斂曲線更平滑，在崎嶇海底地形模型的模擬中表現出較好的適應性。

基于中國南海某海域真實深水(1600～2000m)地形數據，分別建立了常規油氣儲層模型、考慮可燃冰分布的油氣儲層模型及考慮基底起伏的復雜地質模型。通過對這些模型的模擬及分析得出以下認識。

(1)在近收發距區域，海底地形對水平電場的影響較明顯，即使在儲層埋藏較淺的情形下也難以分辨其水平分布范圍；隨著收發距的增加，儲層響應逐漸增大，同時海底地形對電場振幅的影響變小，在地形起伏不太劇烈的情況下可識別儲層的平面分布范圍；當收發距進一步增大，異常體響應隨之減弱，海底地形與油藏響應共同作用，造成電場曲線劇烈震蕩，無法對高阻油藏進行有效識別。

(2)若可燃冰礦體埋藏淺，其電場響應明顯，但會與海底地形耦合，因而只在近收發距區域能比較清楚地識別可燃冰礦體的分布范圍。特別地，可燃冰礦體與油氣儲層的水平分布范圍接近，二者的響應會產生重疊和耦合，則需基于更大收發距的電場數據才能識別出深部高阻油藏。

(3)埋深不同的電阻率異常體，其響應特征會體現在不同收發距范圍的電場數據中。收發距稍大(這是一個相對數值，不同條件對應的適宜收發距會有所不同)條件下的電場數據中，深水油氣儲層的響應依然明顯，而海底地形的影響則可忽略。