深水庫區鐵路多塔矮塔斜拉橋設計施工關鍵技術研究

孫宗磊 陳懷智 潘湘文 張偉偉

(1.中國鐵路經濟規劃研究院有限公司 北京 100844；2.中鐵上海設計院集團有限公司 上海 200070)

1 研究背景

隨著我國高速鐵路橋梁建設的快速發展，大跨度橋梁日益增多，混凝土梁式橋剛度大、噪聲小、成本低、維修養護方便，能很好地滿足高速鐵路對平順性、穩定性、可靠性的要求[1－2]。當跨度需求進一步增加時，可采用梁拱組合及矮塔斜拉橋體系的混凝土橋。矮塔斜拉橋體系受力合理、結構剛度大，跨徑布置靈活、施工方便，工后徐變控制較好，當橋梁跨徑小于300 m時，矮塔斜拉橋在經濟性上更具競爭力[3－5]。近些年矮塔斜拉橋在高速鐵路橋梁建設中發展迅猛，先后建成主跨220 m商合杭鐵路穎上特大橋、主跨178 m京沈客專潮白河大橋及主跨2×200 m黃黃鐵路巴河特大橋等多座高速鐵路大跨度混凝土矮塔斜拉橋。

本文以池黃高鐵三塔矮塔斜拉橋為工程背景，對矮塔斜拉橋索力參數敏感性[6]、主梁局部應力狀態進行分析研究，通過研究得到相關的規律指導結構設計。對懸臂澆筑施工中大節段懸臂澆筑及常規掛籃澆筑進行比選探討，對深水庫區鉆孔樁平臺與圍堰一體化施工技術進行研究。本文的研究結論可以為類似的橋梁設計施工提供借鑒和參考。

2 工程背景

新建池州到黃山高速鐵路設計速度350 km/h，線間距5.0 m，采用CRTSⅠ型雙塊式無砟軌道[7]。太平湖特大橋主橋全長789.7 m，計算跨徑(48＋118＋2×228＋118＋48)m，為雙線三塔矮塔斜拉橋(見圖1)，橋位處水深約35 m。橋梁中塔塔墩梁固結，邊塔塔梁固結，橋墩設支座。主梁采用單箱雙室預應力混凝土變截面箱梁，跨中和中支點梁高分別為6 m、12 m。橋面以上塔高47.2 m，有效塔高(最上排斜拉索理論錨固點到橋面距離)35 m。橋塔形式為矩形直立式，橫橋向寬度2.6 m，順橋向寬度5～8 m。每個橋塔設置9對斜拉索，橫向雙索面布置，塔上索間距為1.2 m，梁上索間距為8 m。斜拉索采用單絲涂覆環氧涂層鋼絞線，每根拉索在橋塔內通過分絲管索鞍通過，錨固于箱梁腹板外側。

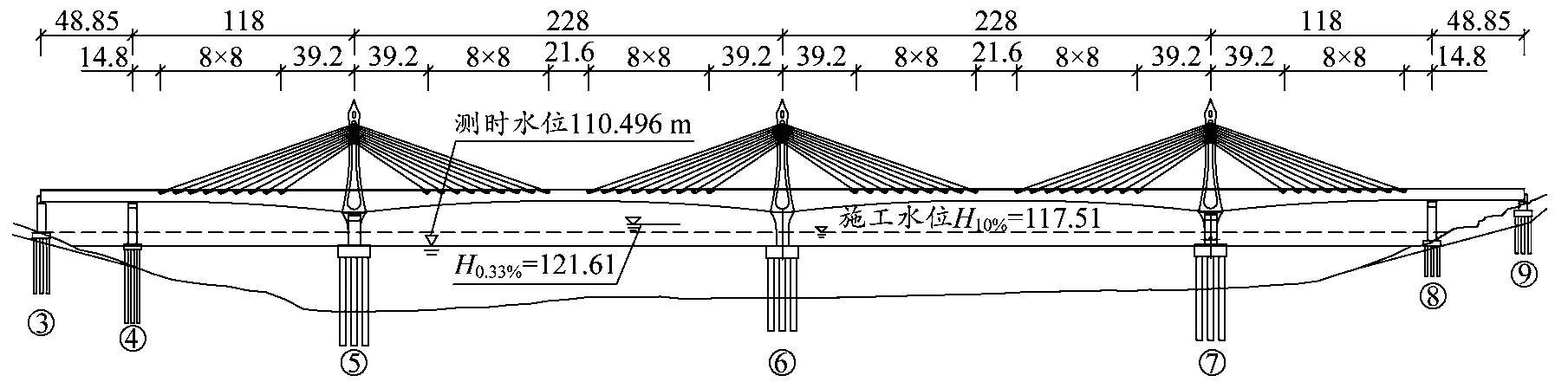
圖1 立面布置(單位:m)

3＃、9＃邊墩采用圓端形實體橋墩，分別采用11根 φ1.5 m、8根 φ1.5 m 鉆孔樁基礎。4＃、8＃輔助墩采用圓端形實體橋墩，均采用14根φ1.5 m鉆孔樁基礎。5＃、7＃邊塔橋墩為矩形實體墩，基礎采用12根φ3 m的鉆孔灌注樁。6＃中塔橋墩為矩形實體墩，基礎采用15根φ3 m的鉆孔灌注樁。三個主塔基礎均采用高樁承臺，自由樁長15～28 m。

3 設計關鍵技術

3.1 斜拉索索力參數敏感性分析

以原設計為基準，分別使索力增加和減少10%、20%，通過模擬計算，研究索力變化對橋梁結構的主梁截面應力和位移的影響。本橋為對稱結構，以中塔為分界線，計算結果只取一半。規定壓應力為負，拉應力為正。圖2a為主力作用下，梁體上下緣最大應力計算結果。圖2b、圖2c為不同索力情況下，相對于原設計主梁上緣和下緣應力的差值。

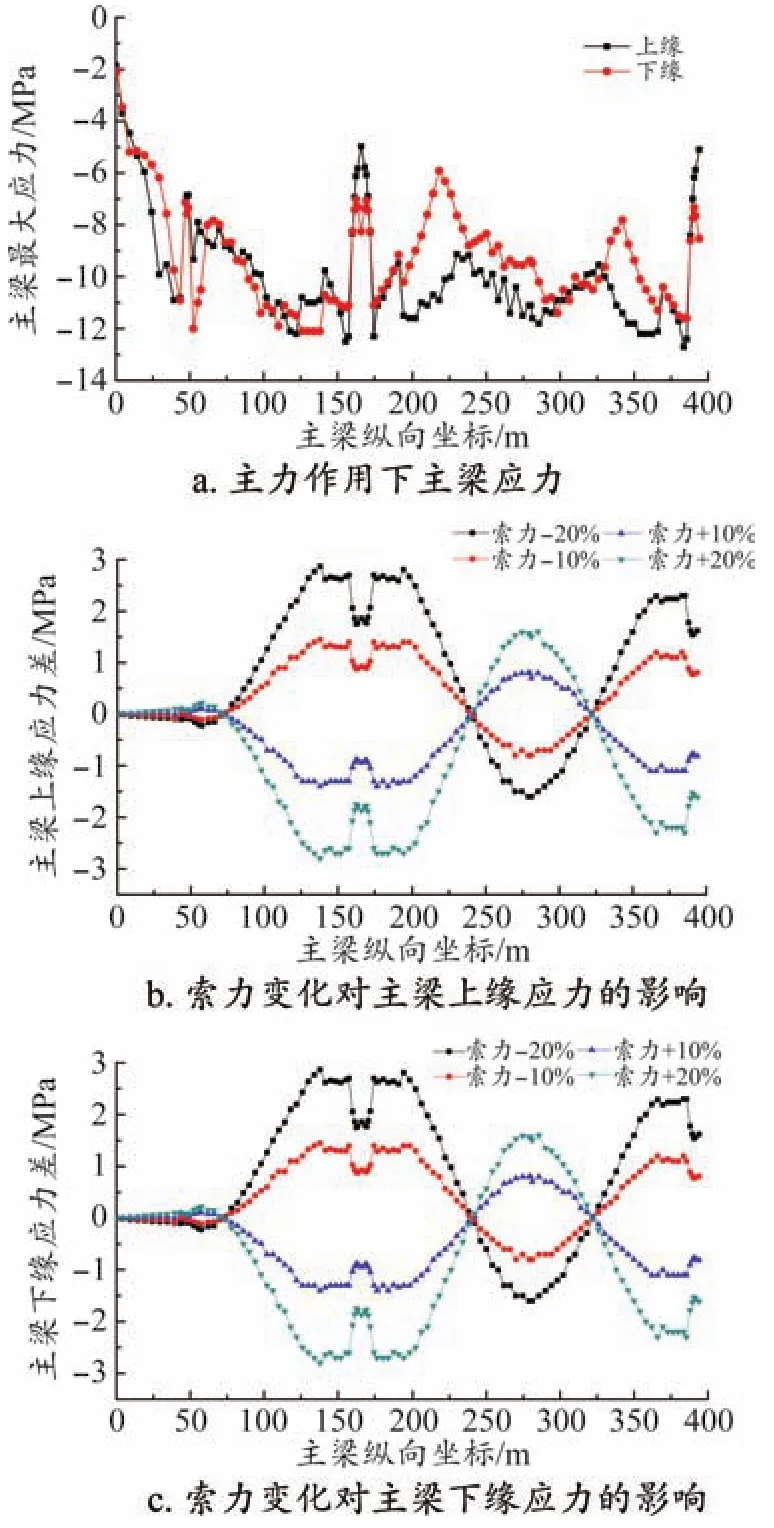
圖2 索力變化對主梁應力的影響

從圖2中可以看出，隨著索力增大，跨中主梁上緣和下緣壓應力均減小，主塔位置主梁上緣和下緣壓應力均增大。

索力每變化10%，塔根無索區梁部上緣應力會產生1.3 MPa變化量，變化幅值為10.5%。跨中位置梁部上緣應力會產生0.8 MPa變化量，變化幅值為7.2%。

索力每變化10%，塔根無索區梁部下緣應力最大會產生1.1 MPa變化量，變化幅值為10.0%。跨中位置梁部下緣應力會產生0.81 MPa變化量，變化幅值為8.6%。

不同索力作用下主梁跨中徐變變形、恒載跨中豎向位移及靜活載跨中豎向位移見表1。豎向位移以向下為負，向上為正。

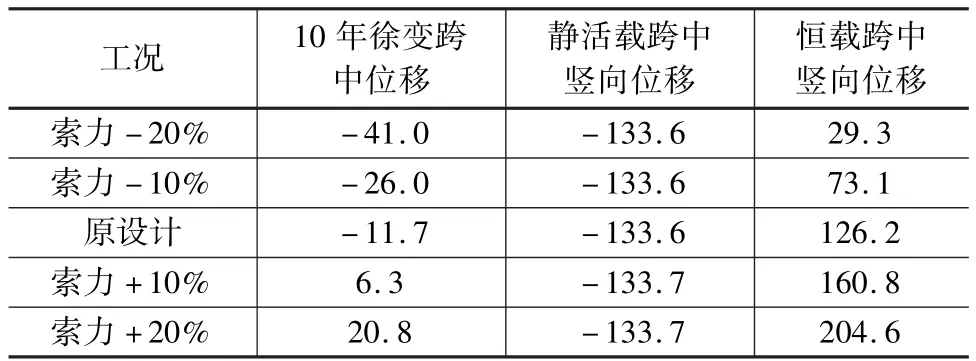
表1 不同索力工況下主梁變形 mm

由表1可以看出索力與徐變變形和恒載跨中撓度呈線性關系，每10%的索力變化會造成跨中最大15 mm徐變變形，53.1 mm恒載變形量。梁體徐變變形變化幅值120%，恒載撓度變化幅度42%。

同時索力變化對靜活載主梁豎向變形沒有影響，因此如不調整拉索規格，索力的增減對成橋后剛度沒有影響。

綜上所述，相較于主梁應力，主梁徐變變形和恒載撓度對斜拉索索力更為敏感，索力變化引起的主梁截面應力變化量不是線性的，具有不均勻性，施工期間斜拉索索力控制要引起重視。

3.2 主梁局部分析研究

矮塔斜拉橋的塔墩梁固結區、索梁錨固區、索塔錨固區等關鍵部位，其受力復雜，桿系單元模型是無法準確計算的，需采用實體有限元結構進行分析計算[8－9]。

綜合考慮計算模型規模，依據圣維南原理，截取所要關注的塊段建立局部實體模型，將全橋桿系模型內力等效施加在截斷處，同時在局部模型中施加相應的約束條件。

3.2.1 局部模型建立

對塔墩梁錨固區，選擇中塔塔墩梁錨固區橫梁兩側各21 m，共42 m梁體及主塔下方的20 m段范圍建立實體有限元模型(見圖3)。

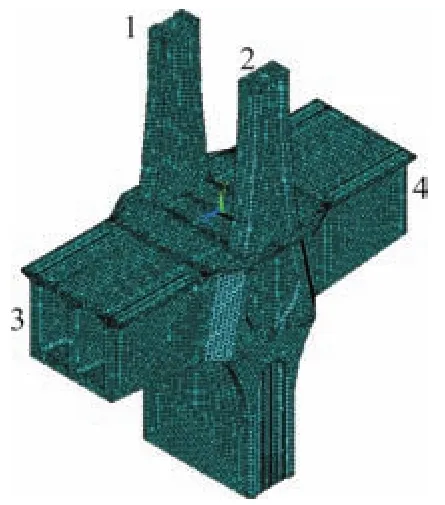
圖3 中塔塔墩梁錨固區有限元模型

將整體桿系模型中提取的截斷位置梁單元內力轉化為節點力作為施加在局部桿系模型的邊界力，見表2、表3，施加位置見圖3。比較同一工況下整體模型與局部桿系模型的內力，如圖4所示，可以看出兩模型的內力趨于一致，差距在5%以內。

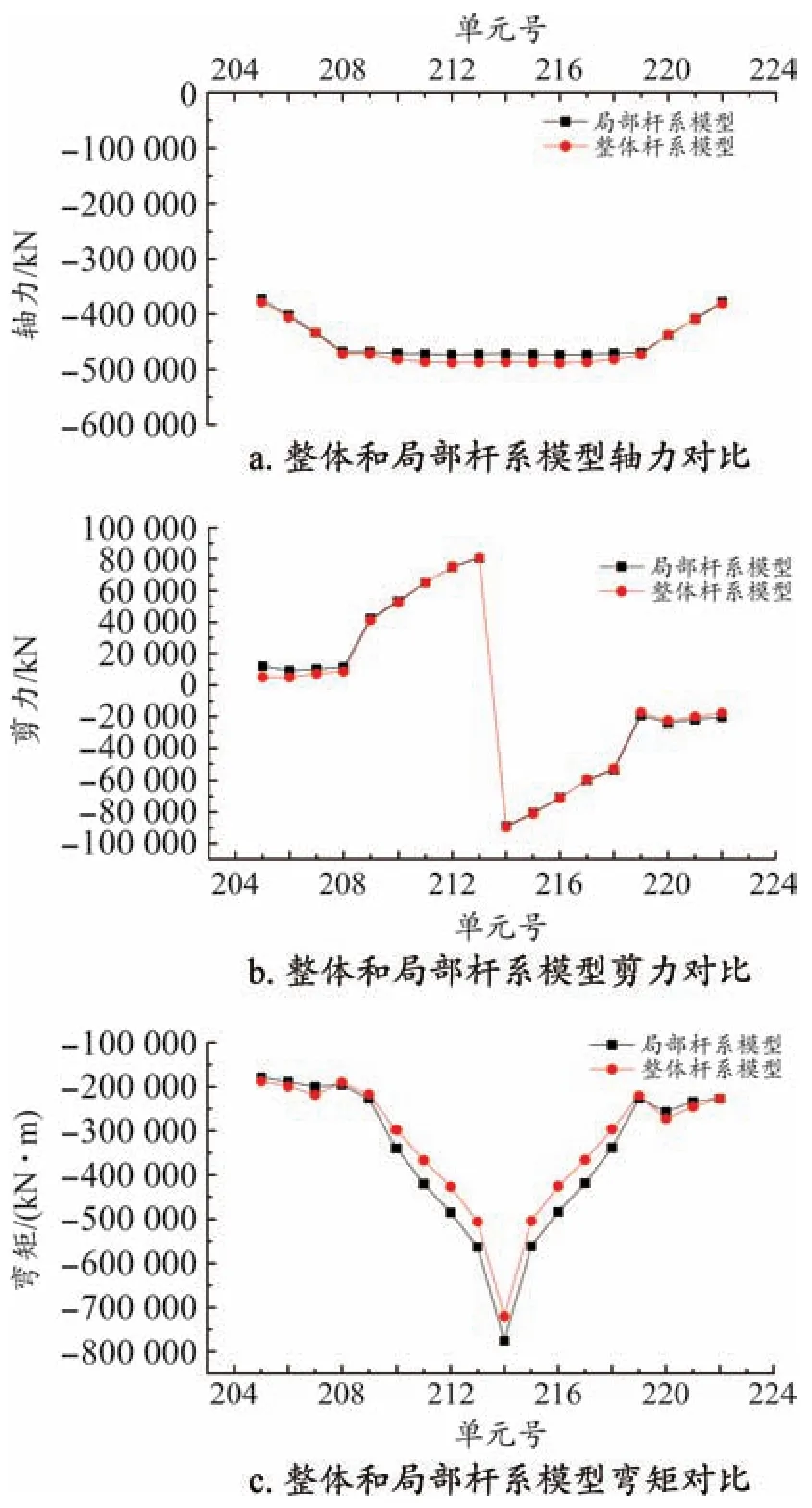
圖4 整體與局部桿系模型內力對比

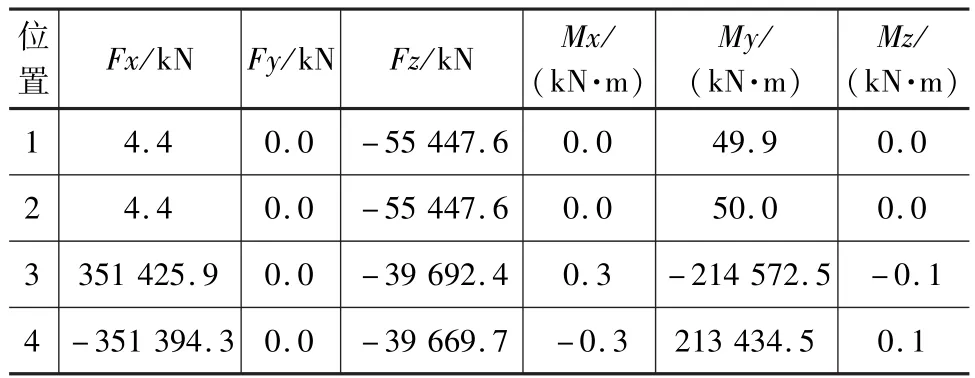
表2 主力組合下邊界力

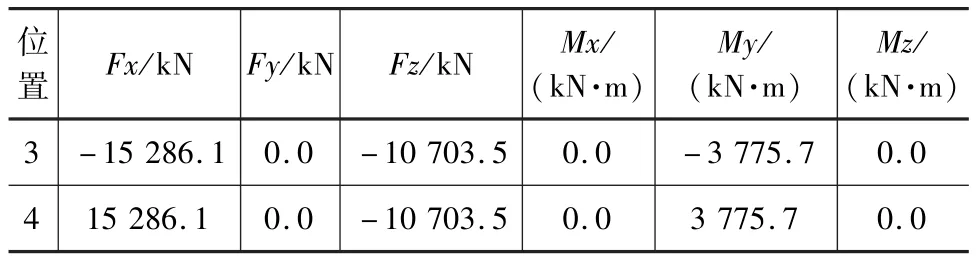
表3 縱向預應力鋼束效應產生的邊界力

內力對比吻合后可將表2、表3中的邊界力作為外荷載加載到實體有限元模型中。

3.2.2 計算結果分析

3.2.2.1 塔墩梁固結區、塔梁固結區

如圖5所示，在主力作用下梁頂、人孔上下側、梁底會出現橫向拉應力，最大拉應力為0.9 MPa。為此，對于塔墩梁固結區或塔梁固結區，設計采取在橫梁梁頂、人孔上下側、梁底設置橫向預應力措施改善受力。

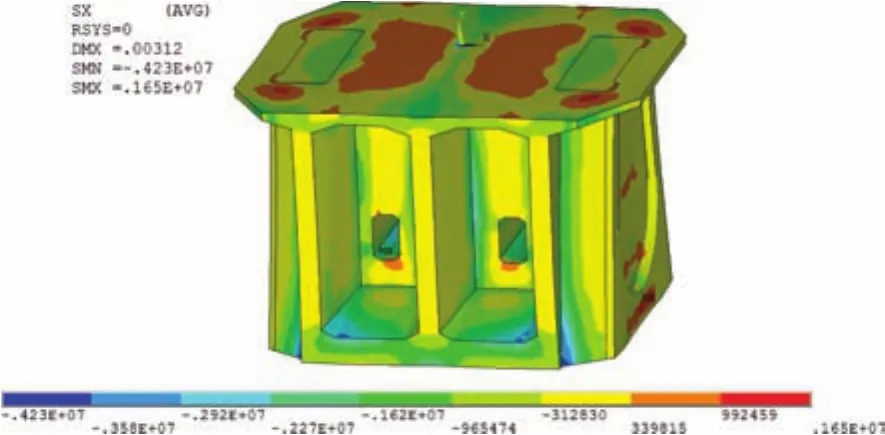
圖5 主力下0號塊橫向正應力云圖(單位:Pa)

3.2.2.2 索梁錨固區(見圖6)

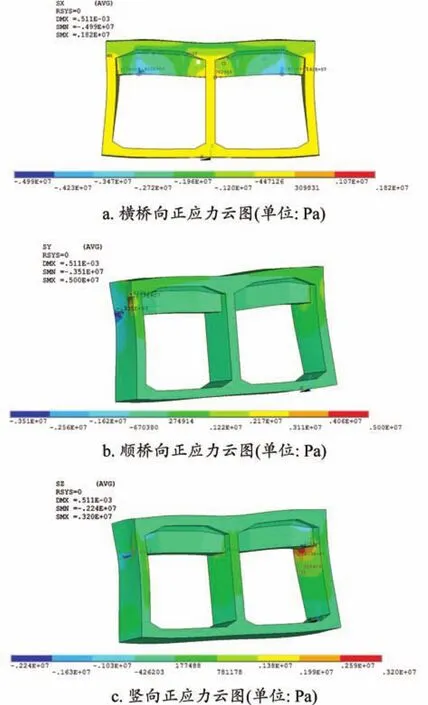
圖6 主力工況下索梁錨固區主梁應力云圖

在索力作用下，錨固橫梁下緣受拉，尤其在錨固橫梁與腹板相接位置，最大拉應力為1.82 MPa。通過在錨固橫梁施加橫向預應力后可有效改善其受力，拉應力需控制在規范[10]限值之內。

在索力作用下，邊腹板出現3.2 MPa豎向拉應力，因此在索梁錨固區的梁段腹板箍筋需要加強。

拉索錨固塊和箱梁腹板相接位置會出現2.0 MPa順橋向局部拉應力，因此錨固塊和箱梁腹板相接位置梁體縱向鋼筋需做加強。

4 施工關鍵技術

4.1 懸臂澆筑施工技術優化研究

預應力混凝土梁懸澆通常采用掛籃施工[11－12]方式，適用于梁體節段長度一般為3～4.5 m。但工期較長，本次對大節段施工造橋機懸澆施工方案(見圖7)進行了研究。

圖7 大節段造橋機

大節段造橋機主要由三片縱向主梁、前橫梁、中橫梁及掛腿、后錨、底平臺、懸吊系統、走行系統等14部分組成。適用最大8 m、最大800 t的懸澆梁段施工。

針對大節段造橋機懸臂施工與常規掛籃，選用如下三個方案進行對比分析。

方案一:掛籃施工，最大節段長4.5 m。

方案二:造橋機施工，最大節段長8 m。

方案三:造橋機施工，最大節段長6 m。

各方案比較結果見表4。

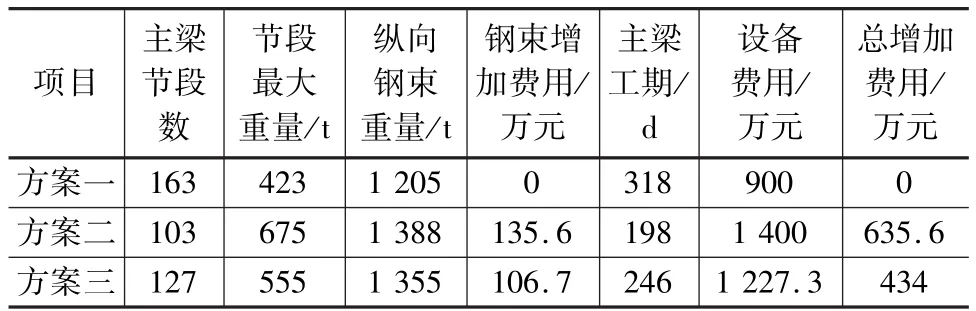
表4 各方案對比

從表4可以看出采用造橋機大節段懸臂施工方案，梁部預應力鋼束含量增加，方案二較方案一預應力鋼束增加15%，同時造橋機設備投入費較掛籃多約500萬，總費用增加635.6萬。但工期可減少4個月。方案三節段長度與斜拉索間距不對應，節段長度變化多，索梁錨固塊多為分段施工，施工復雜。

相較于常規掛籃施工，造橋機大節段懸臂施工會增加一定的工程投資，但可以較大程度減少主梁施工期，是一種值得推廣的新工藝。

4.2 鉆孔樁平臺與圍堰一體化施工技術

橋位處太平湖平均水深約35 m，最深處超過40 m，4＃～7＃墩位于深水區(共 4個墩)，施工難度大、工程風險高。為保證施工工期，提出了利用圍堰作為鉆孔平臺，采用鉆孔樁平臺與圍堰一體化施工方案。

主墩鋼圍堰設計為雙壁鋼吊箱結構，6＃鋼吊箱尺寸為32 m×20 m×18 m，圍堰壁厚1.4 m，見圖8。

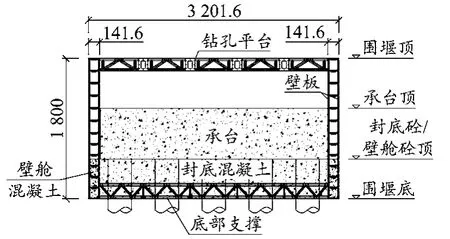
圖8 雙壁鋼吊箱圍堰結構(單位:cm)

鋼吊箱圍堰在岸邊拼裝，拼裝完成后將圍堰滑入水中、插打鋼護筒，下放圍堰并完成浮平臺到固定平臺的轉換，巧妙地將圍堰同時作為樁孔樁平臺和承臺施工的擋水結構，將棧橋施工和圍堰拼裝調整為可平行施工的工序。提升了圍堰拼裝質量，大大縮短工期的同時還節省了樁孔樁平臺的鋼材用量，減少施工投入。

5 結束語

本文對深水庫區多塔矮塔斜拉橋的索力參數敏感性、梁部局部應力、主梁懸臂施工及基礎施工方案進行研究，形成了一整套設計、施工關鍵技術，對今后同類型工程具有借鑒意義，主要結論如下:

(1)多塔矮塔斜拉橋索力對主梁徐變變形和恒載撓度影響突出。索力對主梁線形控制非常重要。

(2)局部實體模型的邊界力可通過提取整體模型的內力求得，并可利用局部桿系模型驗證其正確性。

(3)中支點位置即塔墩梁固結區或塔梁固結區，在主梁橫梁梁頂、人孔上下側、梁底出現橫向拉應力，需要設置橫向預應力改善受力。

(4)索梁錨固區域應力狀態較為復雜，錨固橫梁下緣受拉，可施加橫向預應力改善其受力。該區域邊腹板箍筋、梁體縱向鋼筋需加強。

(5)相較于常規掛籃施工，造橋機大節段懸臂施工會增加一定的工程投資，但可以較大程度減少主梁施工期。

(6)對于深水庫區高樁承臺基礎，采用鉆孔樁平臺與圍堰一體化施工方案可有效縮短施工工期，減少鋼材用量，節約施工成本。