工業純鈦TA2 拉伸及低周疲勞性能的各向異性

梁遠長，常 樂，周昌玉

（南京工業大學機械與動力工程學院,江蘇 南京 210000）

0 引言

工業純鈦是一種具有高比強度、低密度、耐腐蝕特性的材料，不論在航空、航天、艦船、核能等高科技領域,還是在化工、冶金、汽車、建筑、食品等民用工業領域,以及在醫療、體育休閑等民生領域均有廣泛的應用[1-2]。工業純鈦作為各向異性的密排六方體結構（HCP）材料，其各個方向的力學性能差異較大，這種差異來自于冷軋產生的雙峰傾斜基面織構及其獨特塑性變形機制[3-4]。各向異性會顯著影響金屬板材成形性能及質量，如拉深成形過程凸耳的形成。此外，鈦制設備例如鈦制板式換熱器、化工廠反應容器在頻繁開停機、承受疲勞載荷的工況下會出現疲勞失效情況[5]，并且鈦制設備往往同時受內壓及軸向力作用，并非單軸應力狀態，不同方向的疲勞性能存在差異。因此，研究工業純鈦拉伸力學性能及疲勞性能的各向異性具有重要工程意義。

國內外對于密排六方結構（HCP）材料拉伸及疲勞行為的各向異性研究主要集中在鎂合金[6-7]，對于工業純鈦拉伸及低周疲勞性能的各向異性研究非常有限。劉定凱[8]等人討論了不同厚度工業純鈦試樣在RD 方向、RD-45°、TD 方向下的同一應變速率下不同力學性能差異以及不同軋制路徑對板材組織及性能的影響。田晨超[9]等人采用動態接觸式引伸計對純鈦板材靜載拉伸下應變分量進行全程采集，比對分析橫縱向下不同階段塑性變形過程的各向異性，發現純鈦板材縱向（RD）的屈服強度較低，抗拉強度及斷后伸長率則略高。常樂[10-11]為了了解循環不對稱及控制方式對工業純鈦低周疲勞行為的影響，進行了對稱應變和應力控制疲勞試驗，從循環響應、微觀組織演變和疲勞壽命等方面對不同控制方式下工業純鈦沿軋制方向和垂直軋制方向的低周疲勞行為進行了系統比較。由上述文獻可見，對于工業純鈦力學性能的各向異性研究主要集中在RD、TD 方向，未充分考慮RD-TD 平面內取樣角度對于材料力學性能尤其是疲勞性能的影響。此外，不同取樣角度試樣的拉伸本構模型以及疲勞壽命預測仍有待研究。

筆者通過不同取樣方向下的準靜態拉伸試驗，獲取工業純鈦各向異性的拉伸力學性能數據，利用常見的應變率相關的Hollomon 模型[12]及Johnson-Cook[13]模型描述其真實應力情況，并與試驗得到的真實應力應變曲線進行對比。進一步對不同取向試樣進行低周應變控制疲勞試驗，以了解工業純鈦各向異性疲勞性能，并使用能量模型及Manson-coffin模型對疲勞壽命進行預測，為合理、安全使用鈦制設備提供依據。

1 試驗方案

試驗材料為工業純鈦 TA2 板材，材料的化學成分見表1，在室溫下進行試驗，拉伸試樣按照 GB/T 228.1-2010《金屬材料拉伸試驗》標準設計，疲勞試樣參照GB/T 15248-2008《金屬材料軸向等幅低循環疲勞試驗方法》標準設計。拉伸試樣的具體尺寸如圖1 所示，疲勞試樣的具體尺寸如圖2 所示。拉伸及疲勞試樣沿軋制方向（RD）、與RD 呈30°方向（RD-30°）、與RD 呈60°方向（RD-60°）及垂直軋制方向（TD）取樣，具體試樣排布如圖3 所示。對四個加載方向（RD、RD-30°、RD-60°、TD）上均進行不同應變速率拉伸試驗，應變速率分別為5×10-5、5×10-4、5×10-3s-1。然后對應變控制下不同方向試樣進行不同應變幅值下的對稱應變控制疲勞試驗，加載波形為三角波，總應變幅值分別為0.4%、0.6%、0.8%、1.0%。試驗在MTS809 試驗機上進行，使用引伸計對實時應變進行測量。圖4 為母材金相組織，可以看出母材由等軸晶粒組成。

圖3 試樣排布情況Fig.3 Sample arrangement

圖4 母材金相Fig.4 Metallography of base metal

表1 TA2 的化學成分Table 1 Chemical compositions of TA2 %

圖1 拉伸試樣尺寸Fig.1 Tensile sample size

圖2 疲勞試樣尺寸Fig.2 Fatigue sample size

2 試驗結果分析

2.1 拉伸行為研究

2.1.1 力學性能

圖5 分別為屈服強度、抗拉強度、斷后延伸率、屈強比隨加載方向和應變速率變化情況。可以看出，不同取向試樣的屈服強度隨著應變速率的升高而升高，并且隨著取樣角度的增加，不同應變速率下材料的屈服強度增加。抗拉強度同樣隨著應變速率上升而增加，并且RD 方向的抗拉強度反而高于TD 方向。盡管RD 方向試樣屈服強度較低，但是由于其應變硬化能力高于TD 方向，導致其抗拉強度更高[14]。斷后延伸率隨著加載方向的變化并不明顯，隨著應變速率的上升呈現下降的趨勢。為了進一步綜合評價不同取向試樣的塑性變形能力，圖5（d）進一步比較了屈強比的變化趨勢。可以看出，屈強比隨著加載方向由RD 方向變化到TD 方向時，屈強比呈上升趨勢。屈強比為屈服強度和抗拉強度比值，通常來說，屈強比越小，當工作應力高于材料的屈服應力后，由于產生均勻塑性變形，某些應力集中部位的應力重新分布,可減緩或避免脆性斷裂。因而材料均勻、塑性變形能力越強，越不易發生塑性失穩，材料塑性越好。

圖5 TA2 拉伸力學性能隨加載方向和應變速率變化Fig.5 Variations of tensile mechanical properties of TA2 with loading direction and strain rate

2.1.2 真實應力預測

考慮到拉伸過程中試驗試樣因為頸縮導致實際橫截面積的變化，將TA2 拉伸的工程應力-應變曲線轉變為真實應力-應變曲線，轉換公式為:

其中 εt（MPa）為真實應力；εe（MPa）為工程應力；σt（MPa）為真實應變；σe（MPa）為工程應變。Hollomon 本構方程可以很好地描述應變速率敏感性和應變強化對TA2 均勻塑性變形階段（強化階段）應力-應變曲線的影響。表達式如下:

其中m是應變速率敏感性指數;n是應變硬化指數;K值是強度系數。m的值可以通過對TA2 真實應力應變曲線上不同點的真實應力和應變速率取對數，并進行線性擬合得到。n的值可以通過對真實應力應變曲線強化階段選取合適區間，并對此區間的真實應力應變值取對數后進行線性擬合得到。將不同拉伸條件下的應變硬化指數n、應變和應力的值分別代入Hollomon 本構方程，可求出對應的強度系數K值。

在拉伸本構方程中，Johnson-CooK 模型本構方程憑借其形式簡單的優點得到了較為廣泛的應用，JC 本構方程的表達式為：

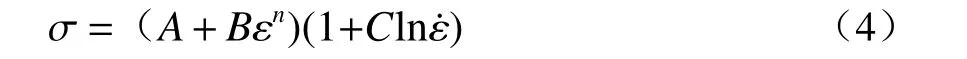
本構方程中包含4 個本構參量，分別為A，B，C，n，均為材料參數，可通過擬合求出。

基于試驗數據，分別利用這兩種模型描述工業純鈦的真實應力應變曲線。圖6 給出了四個加載方向上不同模型預測結果與試驗數據對比，可看出Hollomon 本構模型和試驗得到的真實應力應變曲線幾乎重合，效果較好，而Johnson-CooK 模型在某些強化階段也能達到較好的預測效果。運用統計學參量相對誤差來進行比較，其表達式為：

圖6 Hollomon 本構模型和JC 本構模型預測情況Fig.6 Prediction results of Hollomon and JC constitutive model

其中 σa(MPa)和 σp(MPa)分別是試驗應力與模型預測應力，N為統計樣本的總數。計算出Hollomon 本構模型和JC 模型的相對誤差分別為0.146 1%和1.483 8%。Hollomon 本構方程擬合模型更接近材料的真實應力應變曲線。

2.2 疲勞性能

2.2.1 循環硬化/軟化

圖7（a）為軋制方向上不同應變幅下循環應力幅值隨循環周次演變情況。橫坐標為歸一化的疲勞循環數（N/Nf)。由RD 方向不同應變幅下的應力幅值變化情況，可以看出應力幅值隨著應變幅值的增大而增大，每個應變幅下的應力幅值隨循環周次呈現一個三階段的下降趨勢，初始階段迅速下降，然后緩慢下降，在失效階段又迅速下降的三個階段趨勢，即三個階段的循環軟化。不同應變幅值下其他方向上的應力幅值隨著循環周次演變情況同樣呈現出循環軟化特征。圖7（b）比較了相同應變幅下，不同取向試樣之間循環應力幅差異。根據前文拉伸試驗結果可知，初始塑性變形階段內，隨著取樣角度的增加，工業純鈦的屈服強度逐漸增加。因此，隨著取樣角度增加，材料的循環應力幅值也不斷升高。

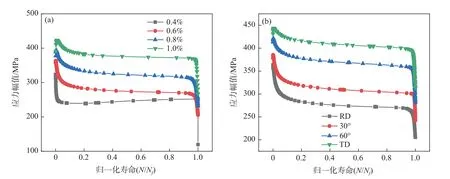
圖7 循環應力幅與（a）應變幅值及（b）加載方向的相關性Fig.7 Dependence of cyclic stress amplitude with (a) strain amplitude and (b) loading direction

2.2.2 疲勞壽命

圖8 為不同應變幅下疲勞壽命隨加載方向的變化情況。可以看出，隨著取樣角度增加，工業純鈦的疲勞壽命逐漸減小。低周疲勞壽命與材料的塑性相關，塑性越好，疲勞壽命越長[15]。拉伸試驗結果已經表明，隨著取樣角度增加，材料的塑性呈下降趨勢。

圖8 疲勞壽命隨加載方向的變化情況Fig.8 Variation of fatigue life with loading direction

2.2.3 應變能密度

應變能密度可分為彈性應變能密度ΔWe+(MJ/m3)、塑性應變能密度ΔWp(MJ/m3)及總的應變能密度ΔWt(MJ/m3)，塑性應能密度ΔWp(MJ/m3)即遲滯回線所包含的面積，可通過對遲滯回線積分求出。Lin[16]等人修正了傳統應變能計算公式，發現與塑性應變能密度相比，總的應變能密度更能反映材料循環變形中累積的損傷對于材料疲勞壽命的不利影響。總應變能密度和彈性應變能密度計算公式為：

其中，σa為應力幅值(MPa)；E為彈性模量(GPa)。

圖9 為工業純鈦總應變能密度隨加載方向和應變幅值變化情況。可以看出，隨著加載方向由RD方向過渡到TD 方向，總應變能密度逐漸增加，說明累積的損傷同樣隨取樣角度增加而增加，導致材料的疲勞壽命逐漸下降。

圖9 總應變能密度隨加載方向和幅值變化情況Fig.9 Variation of total strain energy density with loading direction and amplitude

2.2.4 低周疲勞壽命預測

首先使用總應變能密度來預測材料疲勞壽命，即

其中，Nf為疲勞壽命；k、c的值可以通過擬合獲得，列在表2 中。圖10 為通過總應變能密度預測結果與實際壽命的比較。可以看出，通過總應變能密度預測的結果大多處于兩倍誤差帶內，但仍有少數預測結果處于兩倍誤差帶外。

圖10 基于總應變能密度的疲勞壽命預測與試驗結果對比Fig.10 Comparison between fatigue life prediction by total strain energy density and experimental results

因此，進一步使用常用的Manson-coffin 模型預測不同取向試樣的低周疲勞壽命。Manson-coffin模型的表達式如式（9）（10）所示。

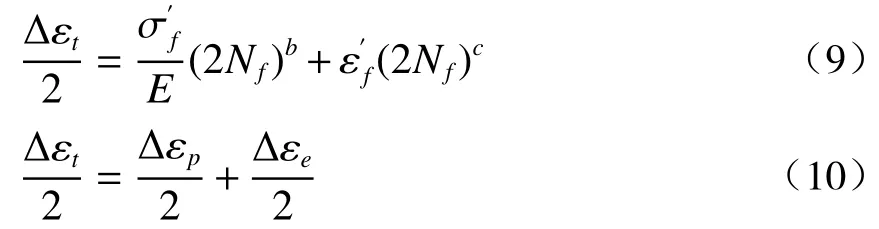
表2 不同疲勞模型參數擬合值Table 2 Fitting values of different fatigue model parameters

圖11 給出了試驗疲勞數據和Manson-coffin 模型預測結果對比。可以看出，在不同加載方向上不同應變幅值的預測數據點都位于兩倍誤差帶內，即Manson-coffin 模型可以更準確預測工業純鈦TA2應變控下不同方向的疲勞壽命。

圖11 Manson-coffin 模型預測壽命與試驗結果對比Fig.11 Comparison between predicted life by Mansoncoffin model and experimental results

3 結論

目前壓力容器設計規范中仍將鈦材按照各向同性材料處理，筆者通過室溫準靜態拉伸試驗和對稱應變控疲勞試驗，研究了工業純鈦TA2 拉伸力學性能和低周疲勞性能的各向異性，得到了不同取樣方向的拉伸本構及疲勞壽命預測模型，以期為相關鈦制設備的各向異性設計提供數據支持及理論基礎。主要結論如下：

1）工業純鈦TA2 拉伸力學性能具有顯著的各向異性，隨著加載方向由RD 方向過渡到TD 方向，屈服強度呈現逐漸上升趨勢，而屈強比逐漸下降，即材料的塑性下降。

2）利用Hollomon 及Johnson-CooK 本構模型預測不同取向試樣的真實應力應變曲線，定量對比結果表明Hollomon 模型預測精度更高。

3）工業純鈦TA2 的疲勞性能具有顯著各向異性。盡管不同取向試樣均呈循環軟化特征，但隨取樣角度增加，循環應力幅值增加，總的應變能增加，導致材料的疲勞壽命呈下降趨勢。

4）利用能量模型及Manson-coffin 模型預測不同取向試樣的低周疲勞壽命，定量對比結果表明Manson-coffin 模型預測精度更高。