延遲退休年齡對居民收入分配的影響
——基于異質性代理人的分析

2022-08-04 08:21:24方守林

人口與經濟 2022年4期

黃乾，方守林

(南開大學經濟學院，天津 300071)

一、引言

二、文獻綜述

目前，關于延遲退休年齡對居民收入分配影響的文獻較少，相關研究包括延遲退休年齡對養老金差距的影響、延遲退休年齡對不同群體收入的影響和優化收入分配的政策建議。黃貞使用阻滯增長模型和1988—2015年社會平均工資與養老金的數據對不同延遲退休年齡下養老金差距進行了預測，預測結果顯示隨著延遲退休年齡的增加，企業、事業單位和公務員之間養老金的差距變小了。延遲退休年齡對在職人員的收入分配也會產生不同影響，比如對新入職人員和藍領工人產生不利影響，對在職人員和白領工人產生有利影響。為了應對延遲退休年齡對居民收入分配差距的影響，應當從完善養老制度、保障老年人的就業權利和盡力縮小收入差距等方面進行收入政策與就業政策的優化。

延遲退休年齡對福利和消費也會產生不同的影響。延遲退休對福利影響的研究表明，延遲退休提高了勞動人口福利和老年人的福利。原政策下本已進入退休年齡段的人群會出現福利下降，其余各年齡段的福利會得到改進。但也有研究表明，延遲退休年齡損害了老年人的福利。延遲退休對居民消費影響的研究表明，延遲退休對消費的影響是積極的。如果資本產出彈性較高，延遲退休將同時降低居民年輕時期和年老時期的消費；反之，延遲退休將降低居民年輕時期的消費，并提高其年老時期的消費和一生中的總消費。

現有研究分析了延遲退休對不同群體收入的影響，并預測了不同延遲退休年齡對養老金收入差距的影響，但是延遲退休年齡對居民收入分配的影響還缺乏深入研究。因此，本文借鑒奧爾巴赫(Auerbach)與克特里克夫(Kotlikoff)的55期世代交替模型(簡稱AK模型)和希爾與莫斯那(Heer and Mauβner)的異質性代理人模型(簡稱BA模型)，構建了80期的異質性代理人模型，用以分析延遲退休年齡對居民收入分配的影響及其宏觀經濟含義。本文模型與前面兩個模型有以下關系：第一，本文構建80期的異質性代理人模型，與AK模型的75期不同。第二，在廠商的生產行為方面，AK模型使用的是CES生產函數，本文使用了CD生產函數，簡化了廠商行為，并沒有納入AK模型中的資本運動方程。第三，本文在勞動力的異質性上主要借鑒了BA模型的設定方法。第四，與BA模型不同，本文的模型更清晰地區分了資本市場和產品市場并定義了模型的均衡與穩態均衡。

三、模型

1. 家庭

每年有相同一代的人出生，將每一代人的數量記為，代表每代人的年齡，所有代人的數量歸一化為1。每一代人最大存活期限為+年，模型中的一期對應一年，其中為工作年限，在該時期居民無彈性地提供勞動力，是退休年限，居民從本期到下一期的存活概率為。居民最大化效用函數如下：

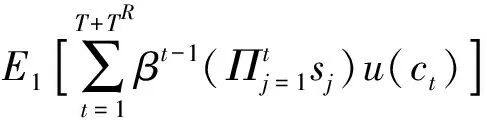
(1)

其中，代表折現率，是居民在年齡為時的消費，是個體在期的存活概率。

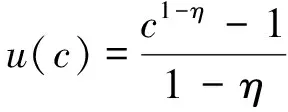
(2)

是家庭的相對風險厭惡系數，其倒數即為消費的跨期替代彈性。則居民的勞動生產率是：

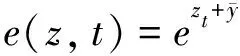
(3)

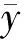
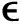
(4)

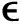
+1=(1+)+(1-)(,)-,=1,2,…,

(5)

其中，和代表利率和工資，代表勞動供給的數量，工資稅率用來表示。退休期間居民獲得的養老金為，則預算約束為：

+1=(1+)+-,=+1,+2,…,+

(6)

在(5)式或(6)式的約束下求解最大化問題，則居民最優化的貝爾曼方程表示為：

(7)

其中，(,)是居民在時期的值函數，狀態變量是時期居民擁有的財富數量和異質性生產率的沖擊，控制變量是居民在期的消費(,)和下一時期的財富+1(,)。則居民財富的演化規律服從以下方程：

+1(+1,+1)=∑∈(+1|)·((+1)(+1,),)

(8)

其中，(+1|)表示生產率狀態從到+1的轉移概率。(+1)(+1,)表示下一期的財富存量+1(,)是第一個變量的反函數。

2. 廠商

廠商的數量歸一化為1，使用規模報酬不變的Cobb-Douglas生產函數進行生產。

=1-

(9)

其中，是生產中使用的勞動數量，是生產中使用的資本數量。廠商利潤最大化問題為：

=1---

(10)

其中，П代表廠商的利潤，是資本的價格，是勞動力工資。根據廠商使用要素的原則，可以得出其使用資本和要素的方程如下:

=(1-)-

(11)

=1--1

(12)

根據的方程和資本折舊率可以得出家庭財富的投資回報率為:

=-=1--1-

(13)

3. 政府

養老保險實行現收現付制，工資收入中比例為的部分用于繳納養老保險，其支出滿足如下等式：

(14)

其中，是每一代人的數量，是退休期間居民獲得的養老金數量。

4. 均衡與模型的求解

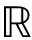
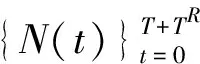
(2)穩態均衡。一個穩態均衡是指一個競爭均衡，并且滿足價格、稅率和政策方程是不變的并且總量變量以穩定的速率增長。

參考希爾和莫斯那的求解算法，本文按照以下步驟使用GAUSS 21對模型進行求解。

Step1：由于人口結構在模型中是外生的，因此，首先計算勞動力的供給總量。

Step2：給定對資本總量和養老保險貢獻率的初值，如可以令的初值等于同質性代理人的值。

Step3：計算廠商最優化問題和政府的預算約束。

Step4：計算家庭的最優化并計算消費和儲蓄的最優路徑。

Step5：計算資本總量，并更新的數值，如果收斂返回，如果不收斂，回到Step3直到收斂。

四、參數校準與模擬

1. 參數校準

本文使用上面建立的異質性代理人模型的校準版本評估延遲退休對居民收入分配的影響，選擇模型的參數使之能夠匹配2018年中國家庭追蹤調查(CFPS)中Gini系數的關鍵特征。CFPS由北京大學中國社會科學調查中心(ISSS)負責實施。CFPS通過跟蹤收集個體、家庭、社區三個層次的數據，反映中國社會、經濟、人口、教育和健康的變遷。校準參數來自于微觀數據計算、宏觀數據計算和文獻中常用的校準參數。我們通過比較基準模型和政策參數計算的不同結果以進行政策分析。

表1 參數及其校準

2. 基準模型評估

本文將以上參數校準的模型稱為基準模型，使用模型進行模擬然后計算Gini系數并繪制洛倫茲曲線，之后與中國家庭追蹤調查(CFPS)的家庭數據進行匹配。基準模型的Gini系數為0.5622，中國家庭追蹤調查的數據為0.4668，基準模型大致能夠匹配實際的數據。基準模型和中國家庭追蹤調查數據的洛倫茲曲線如圖1所示。

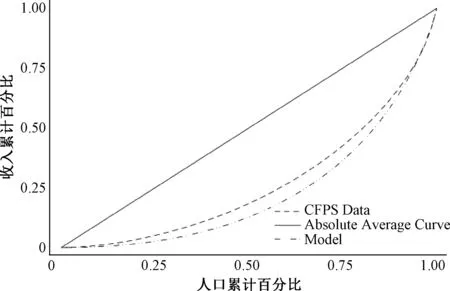
圖1 基準模型與CFPS洛倫茲曲線

模擬結果表明，基準模型的Gini系數稍微高于實際數據的Gini系數，因此圖1中，中國家庭追蹤調查(CFPS)的洛倫茲曲線在基準模型的洛倫茲曲線上方，并且按照洛倫茲曲線的形狀來看基準模型累計收入百分比均低于實際收入百分比。同時本文還模擬了相對風險厭惡系數等于1.0和1.8、替代率為0.2和0.4、資本產出彈性為0.34和0.46時的Gini系數。相對風險厭惡系數為1.0和1.8時的Gini系數分別為0.5526和0.5646。替代率為0.2和0.4時的Gini系數分別為0.5513和0.5698。資本產出彈性為0.34和0.46時的Gini系數分別為0.5677和0.5395。模型中Gini系數稍微高于實際數據，模型匹配的效果較好。在基準模型、相對風險厭惡系數為1.0和1.8、替代率為0.2和0.4、資本產出彈性為0.34和0.46的模型中，穩態時的工資、資本回報率、總消費、Gini系數、總福利、退休人員平均福利如表2所示。

表2的結果表明，相對風險厭惡系數與Gini系數呈正相關,意味著跨期替代彈性與Gini系數呈負相關，跨期替代彈性越高，Gini系數越低，居民收入分配更加平等，直觀上跨期替代彈性增加了消費的流動性從而增加了儲蓄的流動性，進而降低了整體經濟收入和財富分配的不平等現象。替代率與Gini系數呈正相關，替代率越低居民收入分配越平等，直觀上較低的替代率降低了退休之后的不平等。資本產出彈性與Gini系數呈負相關，資本產出彈性越高居民收入分配越公平。

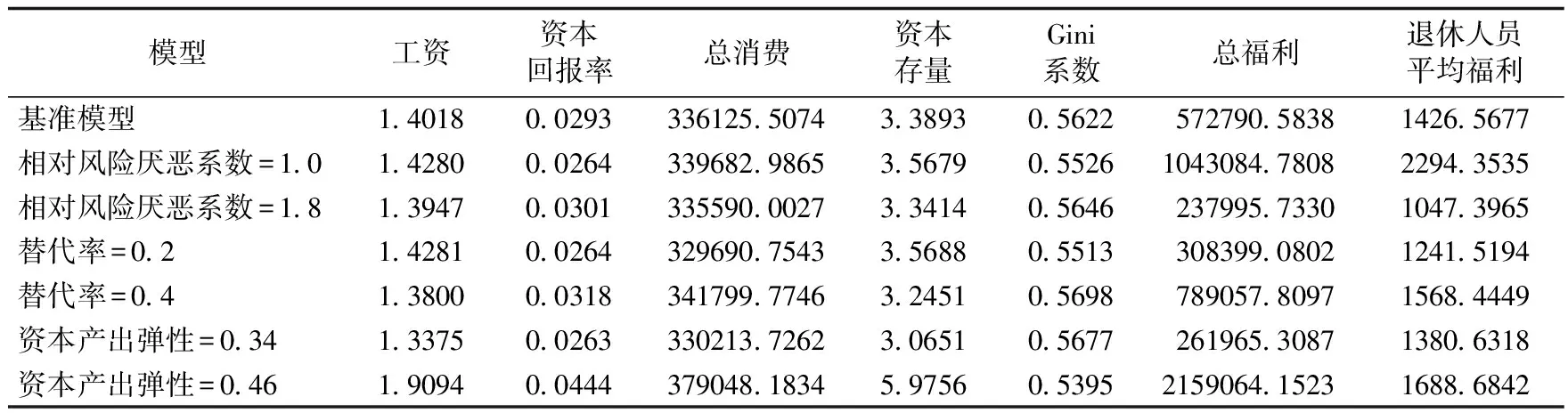
表2 不同模型中的經濟變量和Gini系數

在其他變量方面，當消費的跨期替代彈性較高時，工資水平、總消費、資本存量、家庭總福利和退休人員的平均福利均高于跨期替代彈性較低時的水平，資本回報率低于跨期替代彈性較低時的水平。當替代率較高時具有較高的Gini系數、較低的資本存量、較高的消費和較高的資本回報率、較高的總福利和退休人員平均福利以及較低的工資水平。當擁有較高的資本彈性時，則有較高的工資水平、資本回報率、總消費、資本存量、總福利和退休人員的平均福利。

3. 政策模擬

(1)基準模型。本文首先使用基準模型模擬退休年齡對收入分配的影響。為了分析的簡便，本文假設所有家庭的延遲退休年齡均增加1歲到5歲，分別模擬了退休年齡61歲、62歲、63歲、64歲和65歲對居民收入分配的影響。基準模型的模擬結果如表3所示。

表3 基準模型中不同退休年齡的Gini系數和經濟變量

使用基準模型參數的模擬結果顯示，隨著退休年齡的增加，Gini系數逐漸減小，居民收入分配更加公平。工資水平、資本存量隨著延遲退休年齡降低了，居民的總消費和總福利增加了。退休年齡對退休人員平均福利的影響存在倒“U”型關系，63歲時退休人員的平均福利達到最大值。

(2)養老金替代率。本文模擬了不同替代率下，不同退休年齡的Gini系數和經濟變量，模擬的結果如表4所示。

表4 不同養老金替代率與不同退休年齡的Gini系數和經濟變量

模擬的結果表明，與60歲退休的基準模型相比，在替代率等于0.2時，延遲退休年齡降低了Gini系數，收入分配更加公平，在替代率為0.4時,延遲退休年齡增加了Gini系數，收入分配變得不平等。與基準模型參數的延遲退休年齡相比，在替代率等于0.2時，相同退休年齡的Gini系數更小，收入分配更加平等，在替代率為0.4時，相同退休年齡的Gini系數更大，收入分配不平等程度增加了。但是在養老金替代率為0.2時，居民的總福利和退休人員的平均福利均低于基準模型，養老金替代率為0.4時，居民的總福利和退休人員平均福利高于基準模型。養老金替代率與Gini系數呈正相關關系，并且養老金替代率與居民福利之間存在此消彼長的關系，決策者需要在社會公平和社會福利之間作出權衡。

(3)資本產出彈性。本文模擬了不同資本產出彈性下不同退休年齡的Gini系數和經濟變量，模擬結果如表5所示。

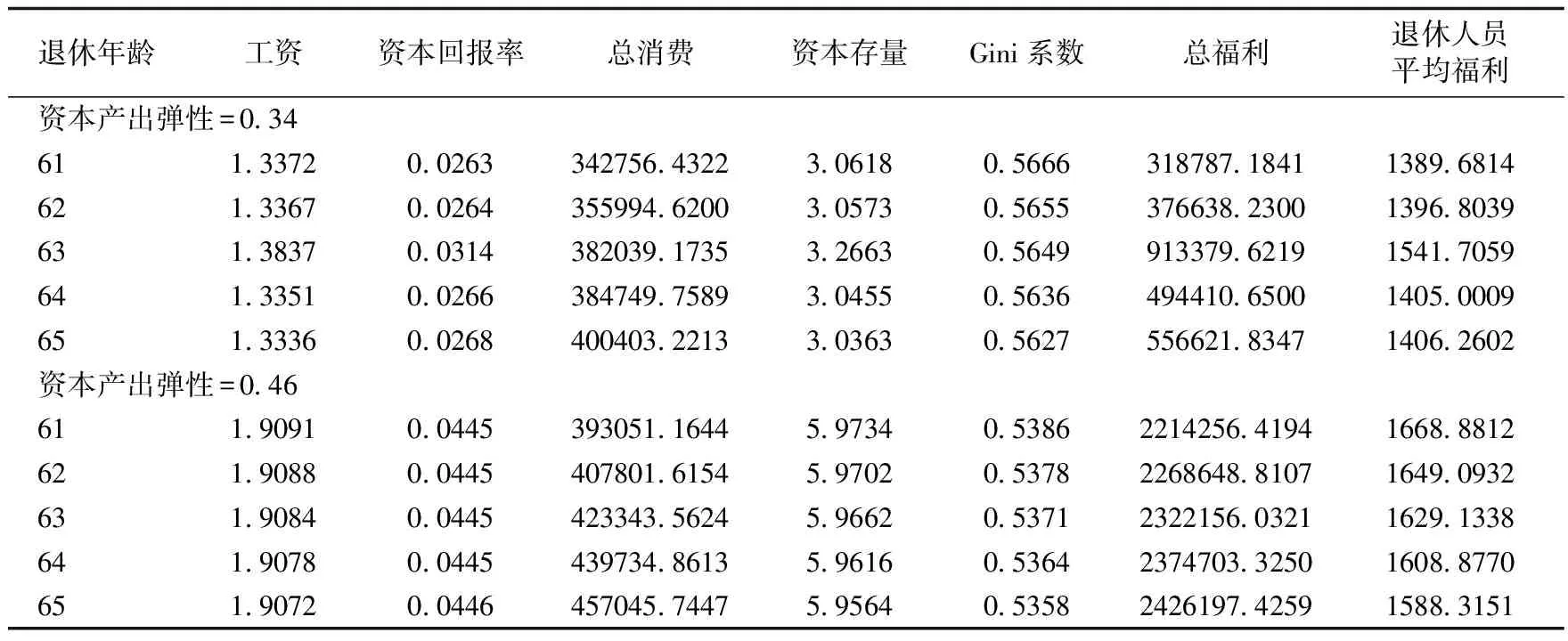
表5 不同的資本產出彈性與不同退休年齡的Gini系數和經濟變量

結果表明，與退休年齡為60歲的基準模型相比，資本產出彈性為0.34時，具有更高的Gini系數，居民收入分配更加不平等，居民的消費、總福利和退休人員的平均福利均低于基準模型。資本產出彈性為0.46時，具有更低的Gini系數，居民收入分配更加平等，居民的消費、總福利和退休人員的平均福利均高于基準模型。與基準參數模擬的各個退休年齡相比，資本產出彈性為0.34時，Gini系數變大了，居民收入分配更加不平等，除了在63歲退休以外，其他退休年齡的福利均低于基準模型。資本產出彈性為0.46時，Gini系數更低，居民收入分配更加平等，居民的總福利和退休人員的平均福利均較高。

(4)相對風險厭惡系數。本文模擬了單位相對風險厭惡模型中不同退休年齡的Gini系數和經濟變量，模擬結果如表6所示。

表6 單位相對風險厭惡模型中不同退休年齡的Gini系數和經濟變量

與60歲退休的基準模型相比，單位相對風險厭惡系數降低了Gini系數，居民收入分配更加平等。單位相對風險厭惡系數模擬的結果表明，隨著退休年齡的增加，Gini系數減小，居民收入分配更加公平。工資水平、資本存量隨著延遲退休年齡降低了，居民的總消費和總福利增加了。在單位相對風險厭惡模型中，隨著退休年齡的增加，所有人的福利也隨之增加，退休人員的平均福利隨之減少。單位相對風險厭惡系數的結果與基準模型類似，但是在相同的退休年齡下，單位相對風險厭惡系數促成了更高的工資、資本存量、總消費、總福利和退休人員平均福利，更低的資本回報率和Gini系數。

五、結論與建議

我國“十四五”規劃和2035遠景目標綱要提出全體人民共同富裕要取得更為明顯的實質性進展。在我國人口老齡化程度逐漸加深和延遲退休年齡的政策背景下，本文通過構建異質性代理人的動態一般均衡模型，使用數值模擬的方法分析了延遲退休年齡對居民收入分配的影響及其宏觀經濟含義。研究結果表明，延遲退休年齡可以降低居民的收入分配不平等，能夠促進共同富裕的實現，并且提高居民的福利水平和退休人員的平均福利水平。研究的主要結論有以下幾點。

第一，延遲退休年齡縮小了居民收入分配差距，有助于實現全體人民的共同富裕。退休年齡延遲越長居民收入分配的Gini系數越小，居民收入分配越公平，并且這一結果在各個參數的模型中均是穩健的。在基準模型中每延遲退休一年，居民收入分配的Gini系數平均降低17%。延遲退休年齡對居民收入分配影響的邊際效應是遞減的，居民收入分配Gini系數對延遲退休年齡的半彈性隨延遲退休年齡的增加而降低。當消費的跨期替代彈性為單位彈性時，隨著延遲退休年齡的增加，居民收入分配的Gini系數減小，每延遲退休一年，居民收入分配的Gini系數平均降低12%，并且居民收入分配Gini系數對延遲退休年齡的半彈性隨延遲退休年齡的增加而降低。相對風險厭惡系數、養老金替代率均與Gini系數呈正相關關系，相對風險厭惡系數越低、替代率越低,居民收入分配越公平。資本產出彈性與Gini系數呈負相關，資本產出彈性越高，居民收入分配越公平。

第二，居民總消費隨延遲退休年齡的增加而增加。這與延遲退休對居民消費具有積極推動作用的研究結論相一致，但是本文的模擬結果表明延遲退休年齡對消費的影響是線性的而不是非線性的。延遲退休年齡增加了總消費，退休年齡延遲越長，居民的總消費越高。在基準參數的模型中，消費對延遲退休年齡的半彈性平均為3.92%，并且隨著延遲退休年齡的增加而增加。居民福利隨著延遲退休年齡的增加而增加，居民福利對延遲退休年齡的半彈性平均為8.49%，并隨著延遲退休年齡的增加而減少。與張艷等的研究結論不同，本文的模擬結果表明，資本產出彈性越高時延遲退休將同時增加居民年輕時期和年老時期的消費，進而增加總消費。其他參數模擬的結果表明，相對風險厭惡系數與居民的消費呈負相關關系，資本產出彈性和替代率與居民消費存在正相關關系。