考慮衛星結構的重型火箭整流罩噪聲研究

趙 華，樂 晨，谷小軍，朱繼宏，張衛紅

(1. 西北工業大學機電學院，西安 710072；2. 北京宇航系統工程研究所，北京 100076；3. 西北工業大學無人系統研究院，西安 10072)

0 引言

在火箭發射過程中，往往會伴隨著嚴重的振動和噪聲，這不僅會引起火箭整流罩內儀器設備出現故障，甚至可能導致發射任務的失敗。因此，研究火箭發射過程中整流罩內的噪聲響應和降噪方案將變得非常重要。

運載火箭發射階段整流罩內的噪聲來源于很多方面，但主要包含兩部分，一是火箭發動機的排氣噪聲以及整流罩與空氣摩擦產生的氣動噪聲,二是火箭結構振動傳遞到整流罩的振動噪聲。通過將兩者疊加，可以得到一個總的整流罩外部噪聲源。

由于整流罩噪聲分析的頻譜很寬，一般被劃分為低頻和中高頻單獨分析。對于低頻，系統的各動力學參數比較確定，結構和聲腔的模態密度也較小，因此一般采用有限元方法進行分析；但是對于中高頻，結構系統較為復雜，系統的各動力學參數具有隨機性，并且結構和聲腔的模態密度比較大，因此常采用統計能量分析(SEA)方法進行分析。如Hwang等采用SEA方法分析了在發射階段聲激勵下火星航天器的聲振響應，在高頻段其仿真與實驗測試結果的聲壓級基本吻合。Larko等運用SEA方法仿真分析了航天器上蜂窩夾層板的高頻聲振響應，仿真與實驗測試結果誤差較小。姚德源等通過SEA方法預測了飛行器圓柱殼儀器艙段聲振環境。孫目等運用Auto SEA2軟件預測了某儀器艙在高頻段的聲振響應以及衛星整流罩內聲場環境，仿真與試驗數據基本吻合。另外，王懷志等采用能量有限元分析(EFEA)方法預示了雙星整流罩中頻聲振環境，并與SEA方法和實驗測試結果進行了對比。曾耀祥等基于SEA方法分析了某火箭儀器艙的聲振環境，并與實驗數據進行了對比。在本文中由于結構系統較為復雜且主要關注整流罩中高頻段內的噪聲響應，因此通過SEA方法對其進行分析。

在以往整流罩的噪聲響應分析和降噪方案研究中，沒有考慮整流罩內有效負載等結構占用聲腔的影響，這勢必會影響整流罩內噪聲響應分析的準確性。本文通過將衛星負載等簡化為圓柱和立方體兩種包絡結構分別在直徑和長度變化下對整流罩內的噪聲響應進行分析。并研究不同降噪材料在不同參數下的降噪效果，給以后的整流罩降噪設計提供一些參考。

1 基于SEA方法的整流罩分析模型

SEA方法是利用統計學的概念研究各子系統之間的能量傳遞和損耗，通過系統振動能量與模態之間的內在聯系建立聲學和結構振動的動力學方程。SEA方法模型的參數主要有：模態密度、輸入功率、內損耗因子和耦合損耗因子。對于有個子系統的SEA模型，當整個系統處于穩態時，可以建立如下能量平衡方程

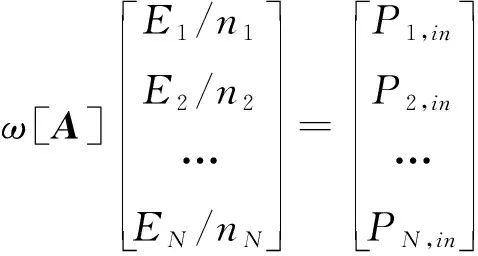
(1)

式中

[]=

(2)

表示分析帶寬內的中心頻率,表示子系統的內損耗因子，表示子系統和間的耦合損耗因子，表示子系統的模態密度，表示子系統的輸入能量，,表示平衡狀態下子系統存儲的能量。

本文采用VAOne軟件進行火箭整流罩噪聲響應的建模和分析，整流罩結構簡化為板殼結構，劃分各子系統時不僅要考慮到實際各子系統的連接，同時為了保證能夠采用SEA方法進行求解，各子系統在分析帶寬內的振型數要大于1。整流罩結構主要為蜂窩夾層板，由于無法在VAOne軟件中直接定義，因此采用三明治夾芯板理論將蜂窩夾層板的夾心結構等效為高度不變的正交各向異性材料板，上下面板保持原有屬性。圖1是整流罩結構在考慮衛星負載下的SEA方法模型(以圓柱形衛星包絡結構為例)，為方便后面討論，對本文關注的圓柱聲腔和部分圓錐聲腔編號1～4。圖2是作用于整流罩外部的聲壓載荷，表1和表2分別是蜂窩結構的尺寸參數和材料參數。

(a) 結構子系統

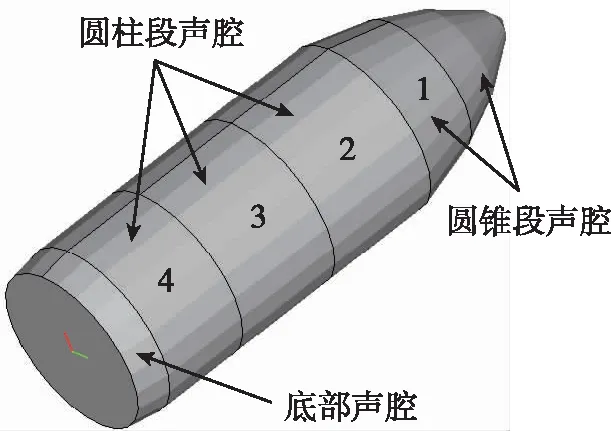
(b) 聲腔子系統圖1 整流罩SEA模型Fig.1 Statistical energy analysis model for fairing

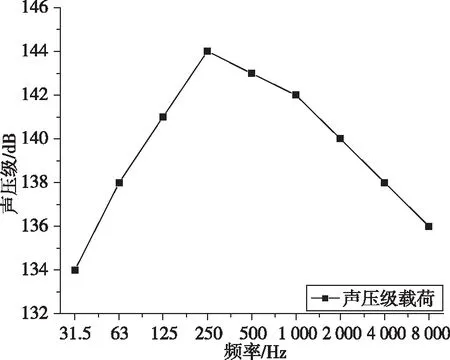
圖2 整流罩外部的聲壓載荷Fig.2 Sound pressure loads acting on the fairing

表1 蜂窩結構的尺寸參數Tab.1 Dimensional parameters of honeycomb structures

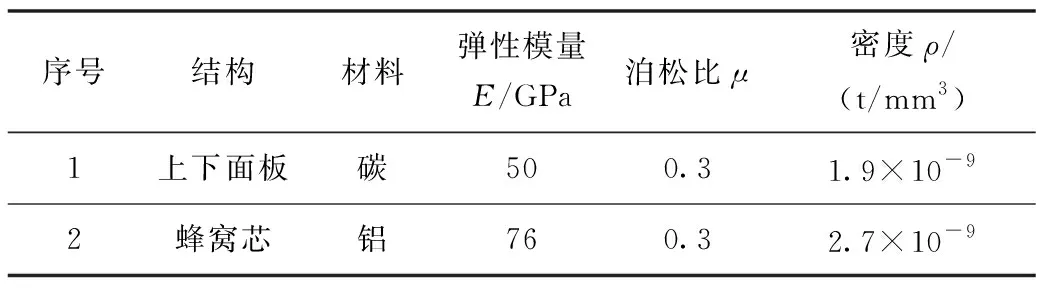
表2 蜂窩結構的材料參數Tab.2 Material parameters of honeycomb structures

2 火箭整流罩的噪聲響應分析

為使仿真結果更加準確，因此需要考慮整流罩內衛星等有效負載結構對噪聲響應的影響。整流罩內衛星結構形式非常復雜，給建模帶來不小困難，因此，在VAOne軟件建模中將衛星結構簡化為圓柱或立方體的包絡形式。對兩種簡化形式分別進行仿真分析，討論隨包絡結構尺寸改變的聲壓級變化規律，以便為后續整流罩內衛星的排布提供一些參考。

2.1 圓柱形衛星包絡結構的噪聲響應分析

針對圓柱形衛星包絡結構，分析不同直徑和高度下的噪聲響應結果。其中，直徑分別為4,5,6 m，高度分別為5,10,13 m。

2.1.1 直徑變化對圓柱(錐)聲腔聲壓級的影響

在原始模型的基礎上僅改變圓柱形衛星包絡結構的直徑，分別在高度為5,10,13 m這3種情況下分析直徑的變化對圓柱(錐)聲腔聲壓級的影響。分析結果如圖3所示，在相同高度下，圓柱(錐)聲腔的聲壓級隨著直徑的增大而減小，表明直徑的增加有利于圓柱(錐)聲腔聲壓級的降低。

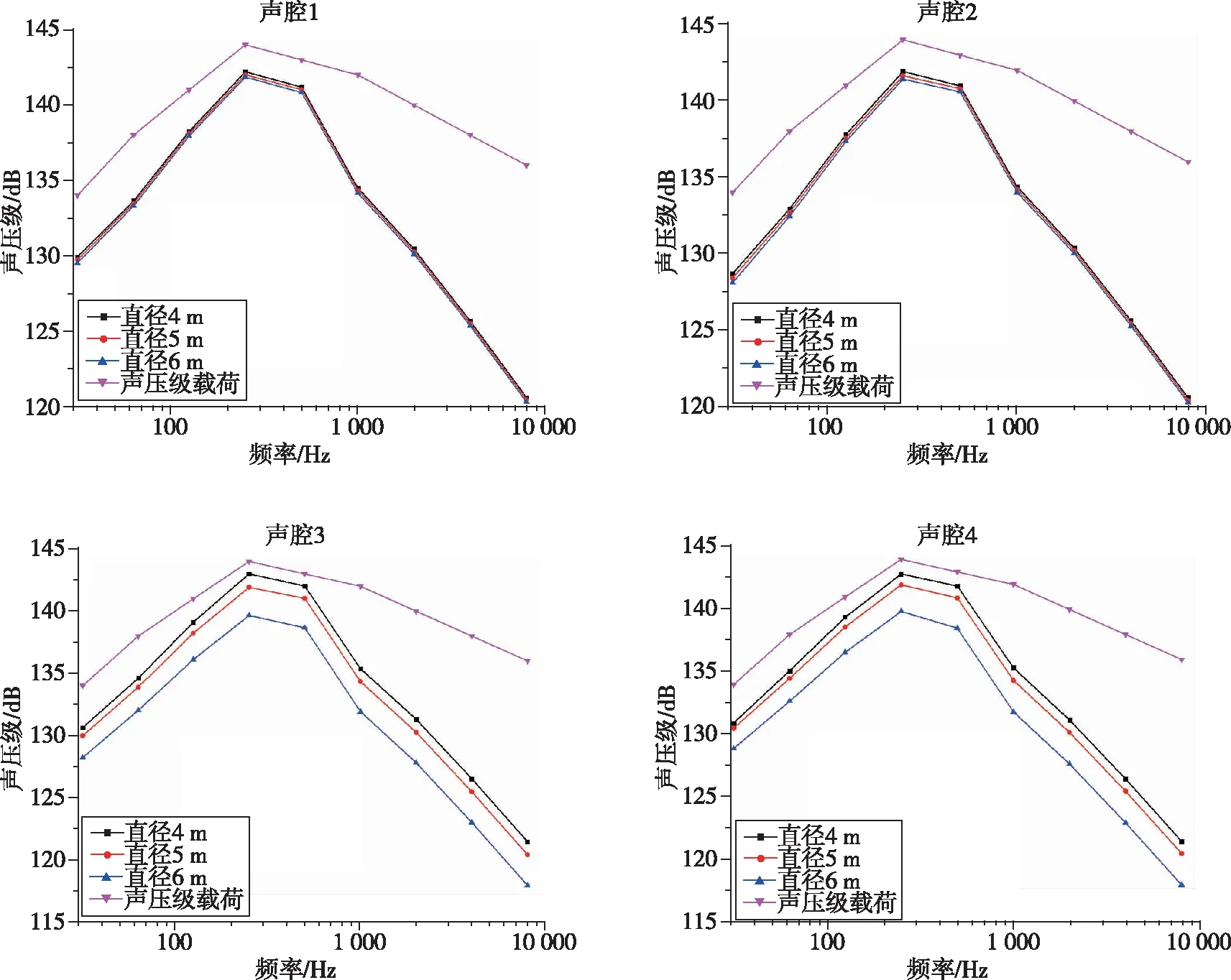
(a) 高度5 m

(b) 高度10 m

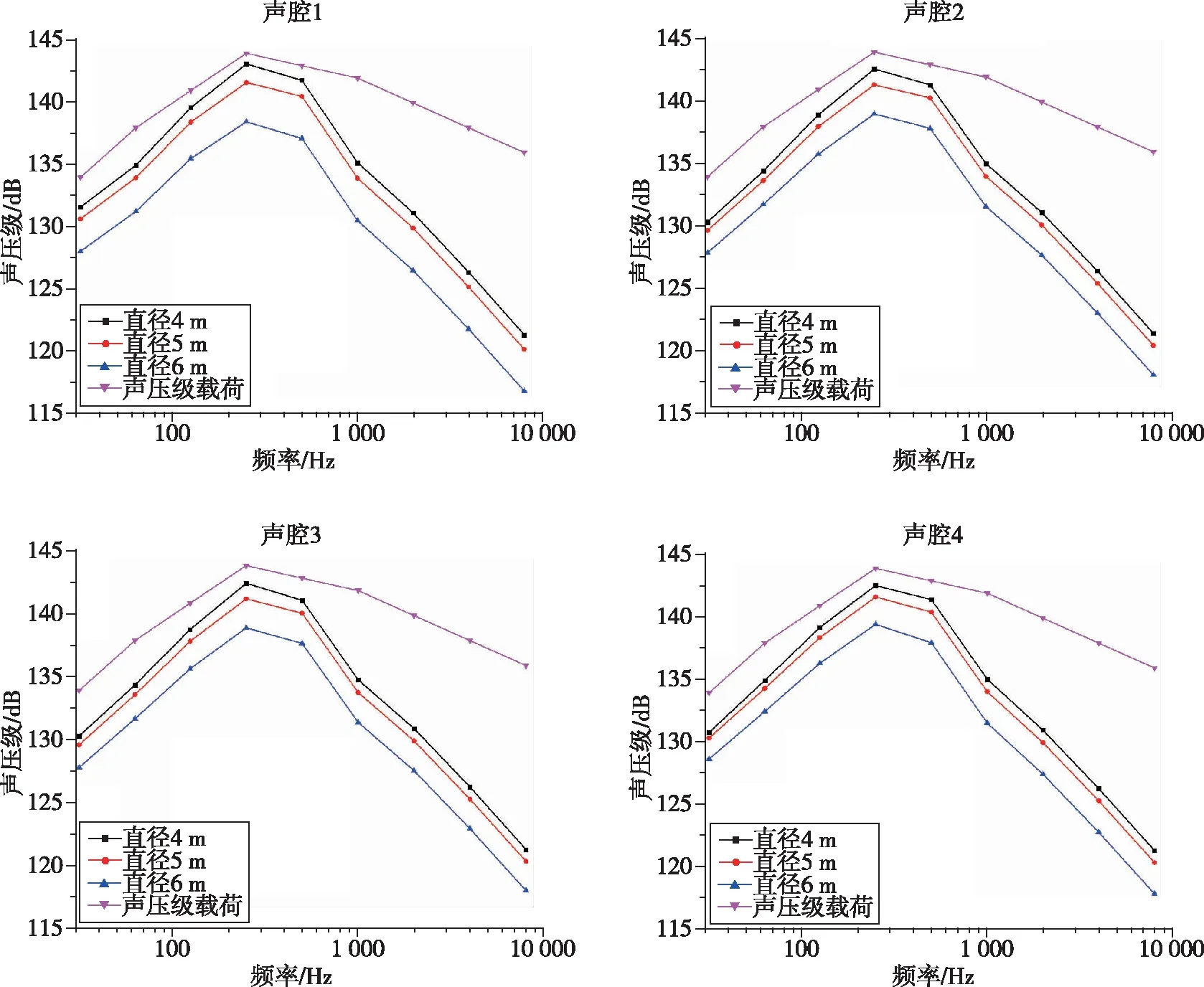
(c) 高度13 m圖3 相同高度下圓柱(錐)聲腔聲壓級隨直徑的變化規律Fig.3 Variation of sound pressure level with diameter for a cylindrical (conical) cavity at the same height

2.1.2 高度變化對圓柱(錐)聲腔聲壓級的影響

同理，在原始模型的基礎上僅改變圓柱形衛星包絡結構的高度，在直徑分別為5 m和6 m的情況下分析高度變化對圓柱(錐)聲腔聲壓級的影響。分析結果如圖4所示，在相同直徑下，各圓柱(錐)聲腔的總聲壓級隨著高度的增加大部分呈降低的趨勢，表明高度的增加有助于降低各聲腔的總聲壓級。

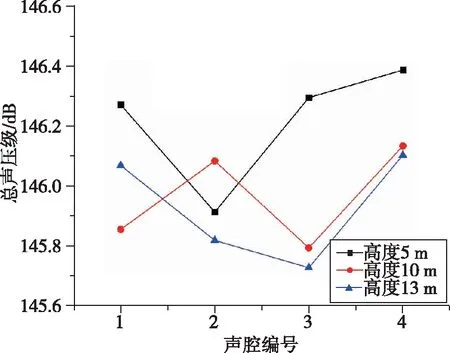
(a) 直徑5 m

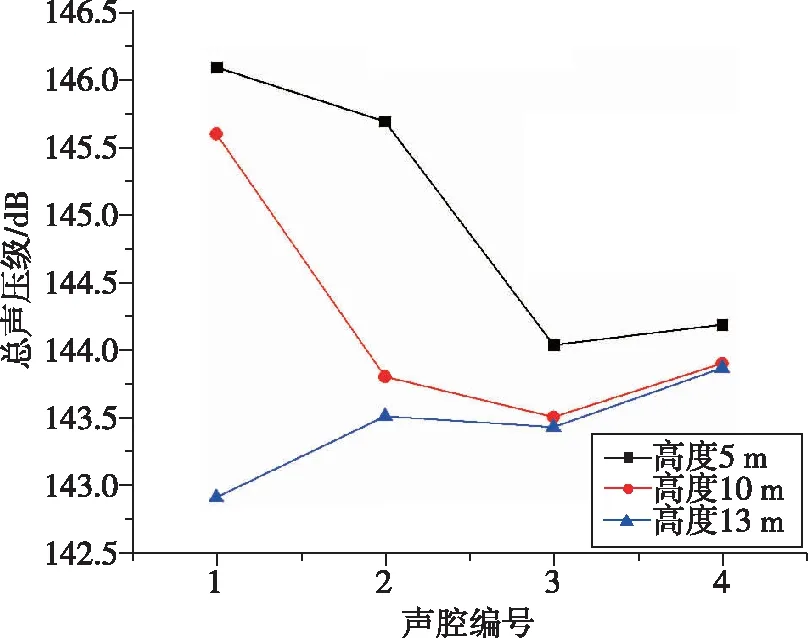
(b) 直徑6 m圖4 相同直徑下圓柱(錐)聲腔聲壓級隨高度的變化規律Fig.4 Variation of sound pressure level with height for a cylindrical (conical) cavity at the same diameter

2.2 立方體形衛星包絡結構下的噪聲響應分析

針對立方體形衛星包絡結構，分析立方體不同底面對角線長度和高度下的噪聲響應結果。其中，底面對角線長度分別為4，5,6 m，高度分別為5,10,13 m。

2.2.1 底面對角線長度變化對圓柱(錐)聲腔聲壓級的影響

與圓柱形衛星包絡結構下的分析方式一樣，通過控制變量法，在高度分別為5,10，13 m這3種情況下分析底面對角線長度的變化對圓柱(錐)聲腔聲壓級的影響。分析結果如圖5所示，在相同高度下，圓柱(錐)聲腔的聲壓級隨著底面對角線長度變化沒有明顯改變。

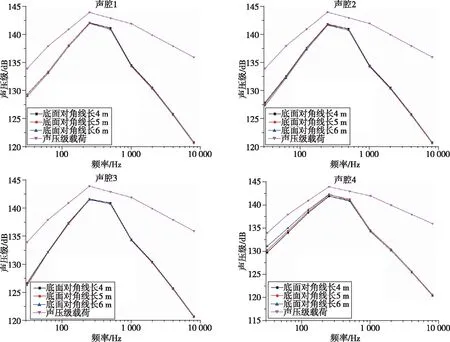
(a) 高度5 m

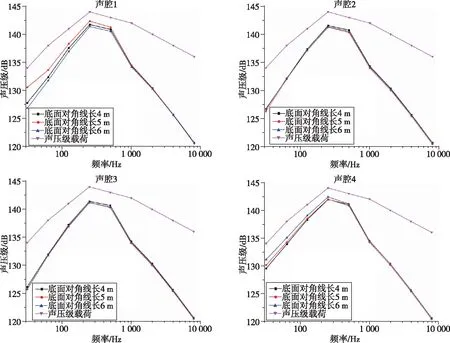
(b) 高度10 m

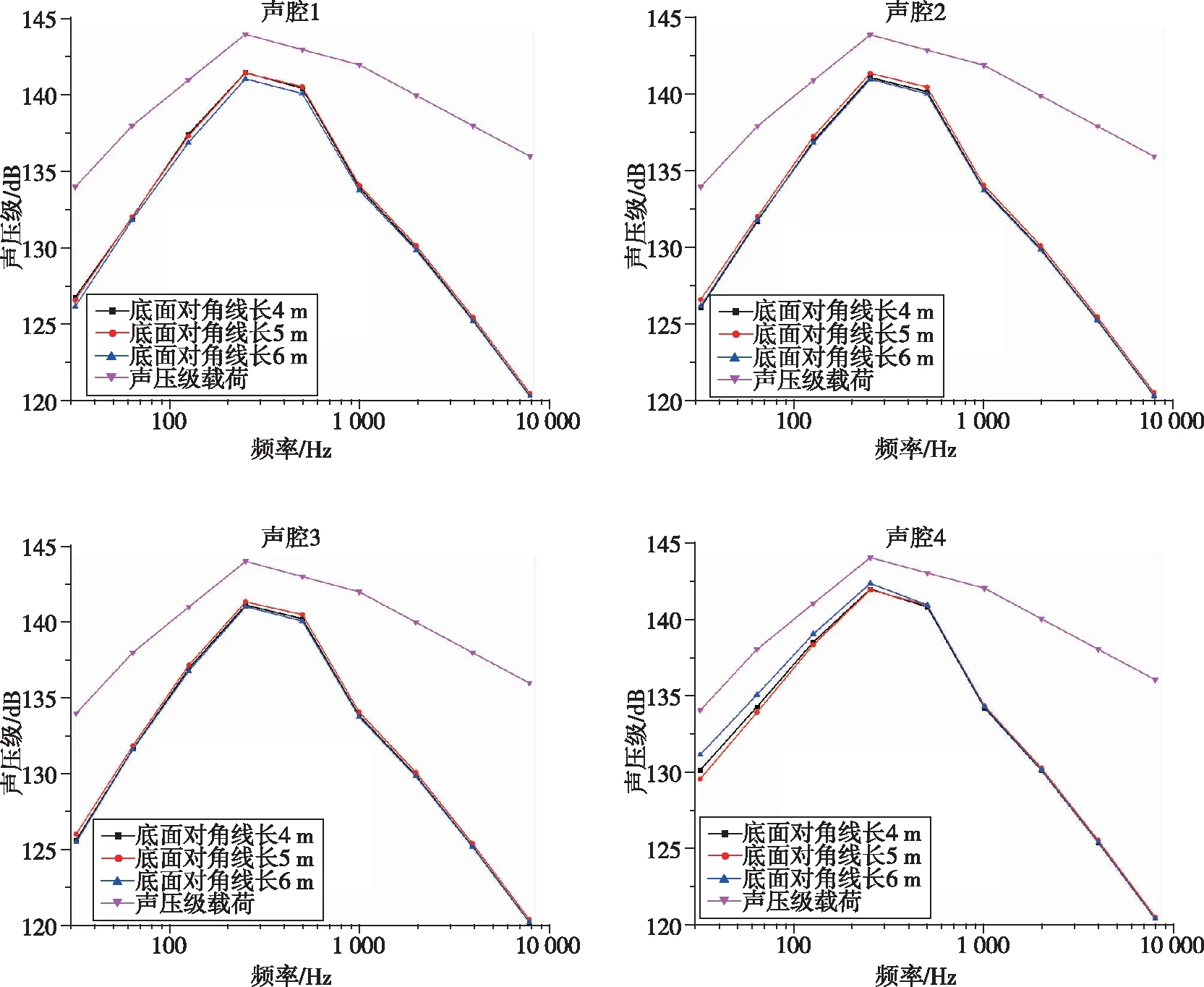
(c) 高度13 m圖5 相同高度下圓柱(錐)聲腔聲壓級隨底面對角線長度的變化規律Fig.5 Variation of sound pressure level with the diagonal length of the bottom surface for a cylindrical (conical) cavity at the same height

2.2.2 高度變化對圓柱(錐)聲腔聲壓級的影響

針對立方體衛星包絡結構，在底面對角線長度分別為5 m和6 m的情況下分析高度變化對圓柱(錐)聲腔聲壓級的影響。分析結果如圖6所示，在相同底面對角線長度下，隨著高度的增加，各圓柱(錐)聲腔的總聲壓級呈降低的趨勢。

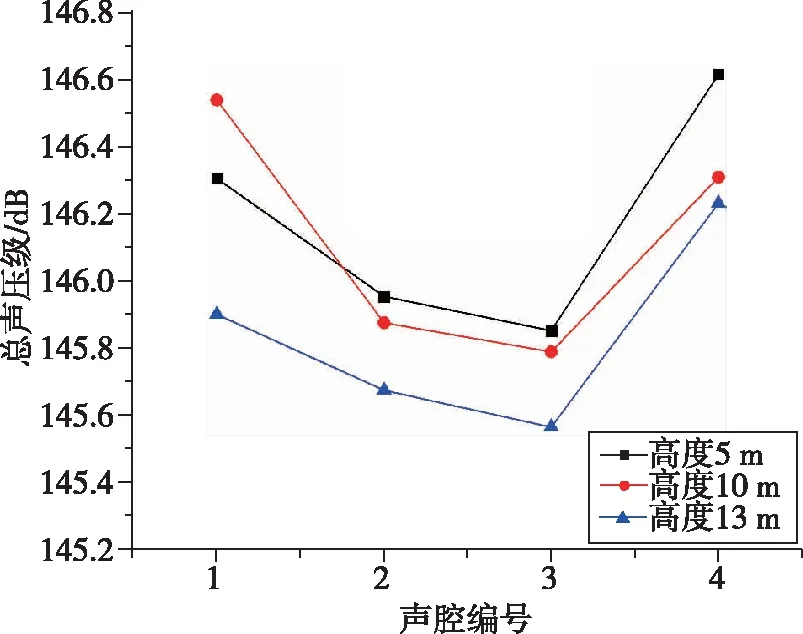
(a) 底面對角線長度5 m

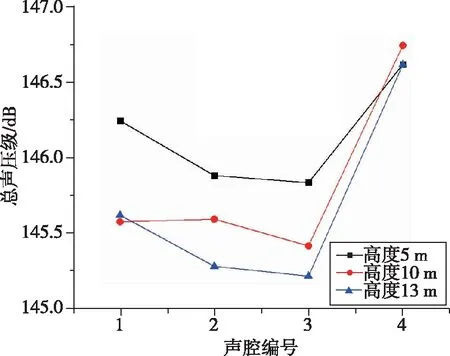
(b) 底面對角線長度6 m圖6 相同底部對角線長度下圓柱(錐)聲腔聲壓級隨高度的變化規律Fig.6 Variation of sound pressure level with height for a cylindrical (conical) cavity at the same diagonal length of the bottom surface

3 降噪材料對整流罩噪聲響應的影響

對于整流罩的減振降噪，主動控制或者半主動控制對于低頻噪聲有比較好的降噪效果，但由于成本和結構的復雜性，實際實施起來有些困難。因此，對于中高頻段噪聲可以采用較為簡便的被動吸聲的方法進行減振降噪，其中泡沫和纖維材料在實際應用當中的效果比較突出。

以直徑和高度均為5 m的圓柱形衛星包絡結構為分析模型，下面針對3種不同材料的降噪效果進行分析討論。圖7表示3種材料在不同鋪設厚度下的整流罩聲壓級響應值，并且與未鋪設降噪材料下的整流罩聲壓級響應值進行對比，分析3種不同降噪材料的降噪效果，圖8對3種材料不同鋪設厚度下的總聲壓級和質量進行了對比。

從圖7和圖8結果中可以發現：1)在較低頻率時，降噪材料對整流罩內聲壓級響應的影響十分微弱，僅在1 000 Hz以上時聲壓級響應隨厚度變化有較為明顯的改變，且隨著厚度的增加而愈發明顯。2)在相同厚度下，毛氈和玻璃纖維的質量相同且相比于三聚氰胺泡沫更重，但同時發現毛氈和玻璃纖維的降噪效果也更為明顯。因此，若要從玻璃纖維、毛氈和三聚氰胺泡沫中選擇最優的一種，則需要比較三者單位質量下的降噪值(降噪值指鋪設降噪材料與未鋪設降噪材料下的總聲壓級的差值)。

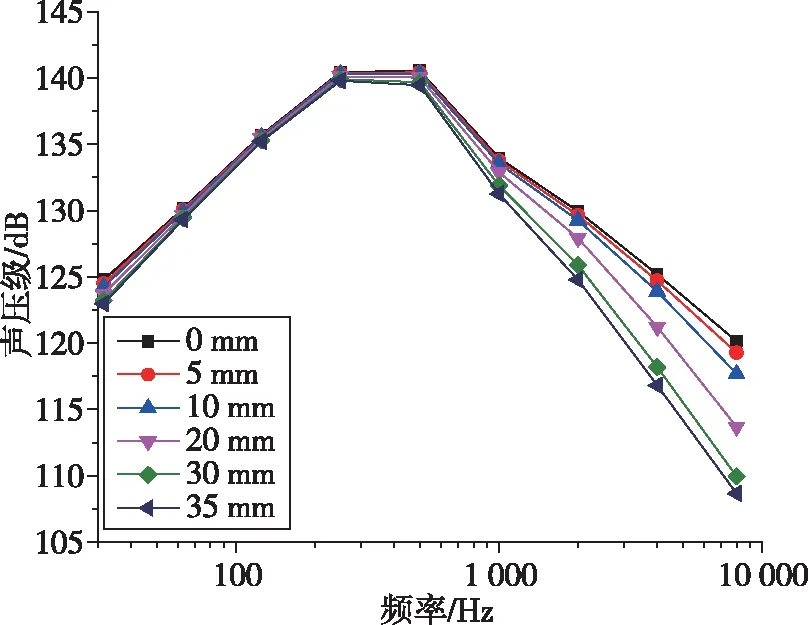
(a) 玻璃纖維

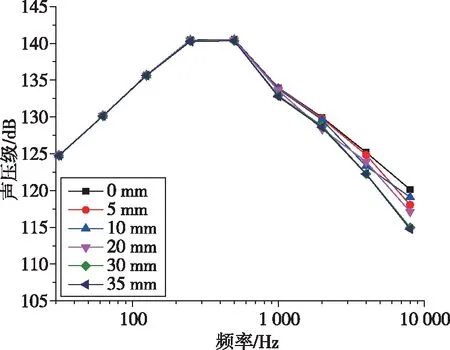
(b) 三聚氰胺泡沫

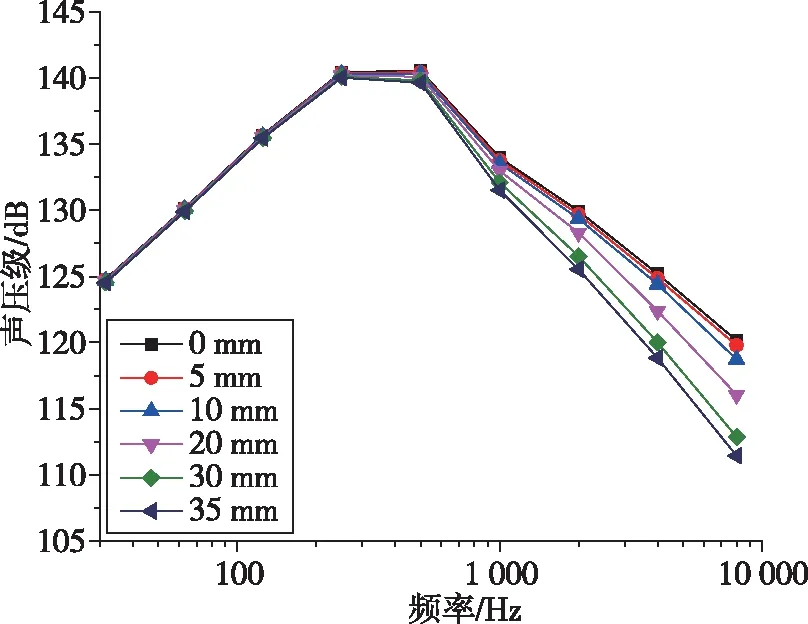
(c) 毛氈圖7 降噪材料在不同鋪設厚度下整流罩的聲壓級響應隨頻率的變化規律Fig.7 Variation of sound pressure level response of fairing with frequency under different laying thickness of noise reduction material

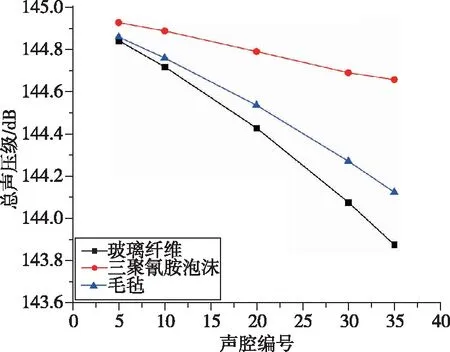
(a) 不同厚度下的總聲壓級

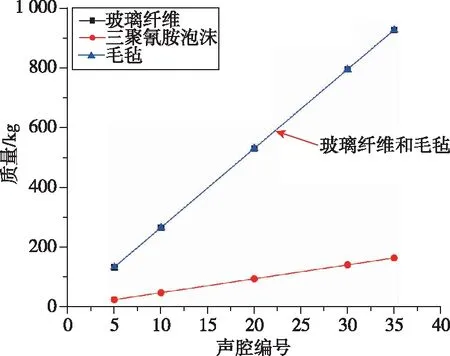
(b) 不同厚度下的質量圖8 降噪材料在不同鋪設厚度下總聲壓級響應和質量對比Fig.8 Comparison of total sound pressure level response and quality of noise reduction materials at different laying thicknesses

表3～5分別是3種不同材料在不同鋪設厚度下的降噪值、質量和單位質量下的降噪值，圖9是3種材料在不同厚度下的降噪值及單位質量降噪值的曲線圖。從中可以發現：1)在相同厚度下，玻璃纖維、毛氈、三聚氰胺泡沫的降噪值依次降低，并且玻璃纖維和毛氈降噪值隨厚度增加更為明顯，而三聚氰胺泡沫降噪值隨厚度的增加變化則較為平緩。2)三聚氰胺泡沫的單位質量降噪能力明顯高于玻璃纖維和毛氈，但在相同厚度下的降噪能力則明顯弱于玻璃纖維和毛氈。因此，在有降噪值和鋪設降噪材料厚度要求時則需要綜合考慮降噪值、質量和單位質量降噪值，以獲得最優的降噪材料鋪設方案。

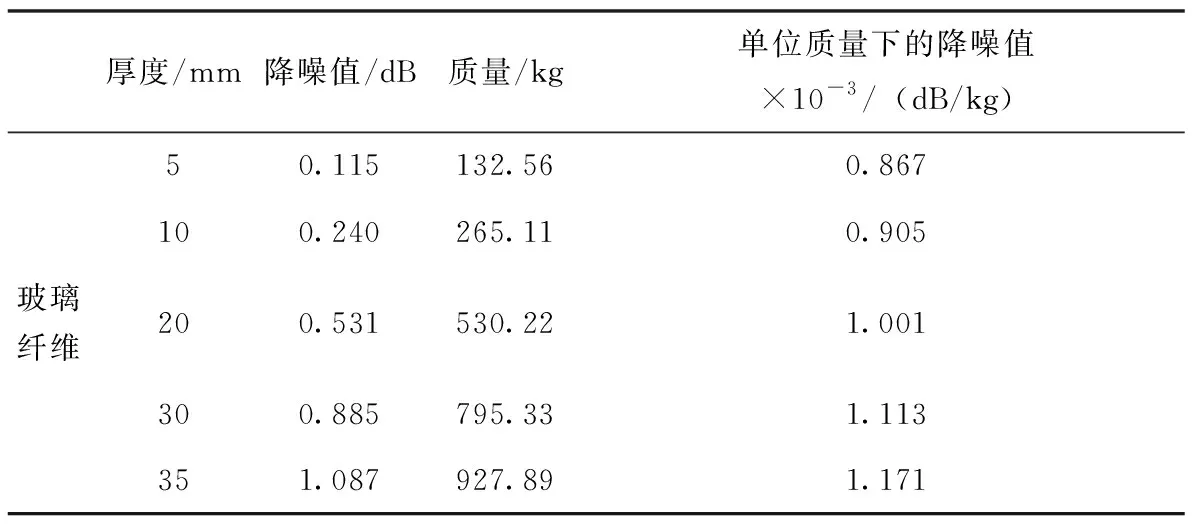
表3 單位質量玻璃纖維的降噪值Tab.3 Noise reduction value of glass fiber with per unit mass

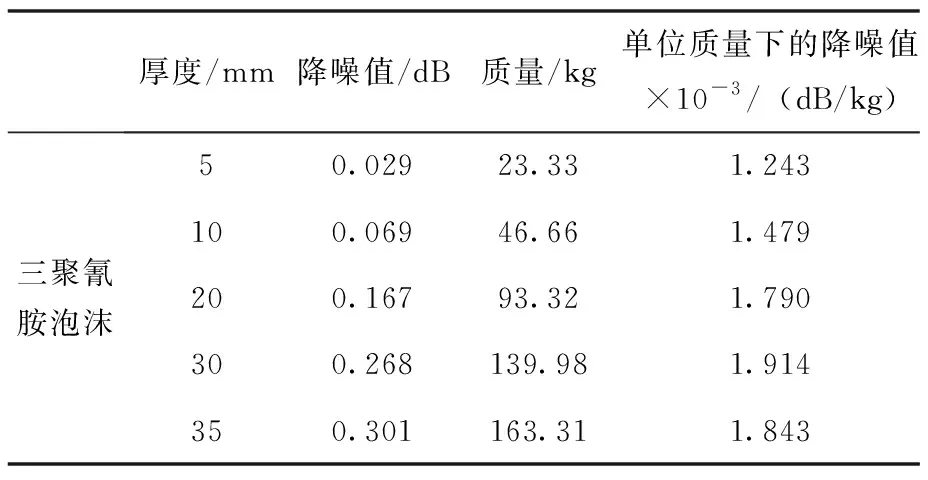
表4 單位質量三聚氰胺泡沫的降噪值Tab.4 Noise reduction value of melamine foam with per unit mass

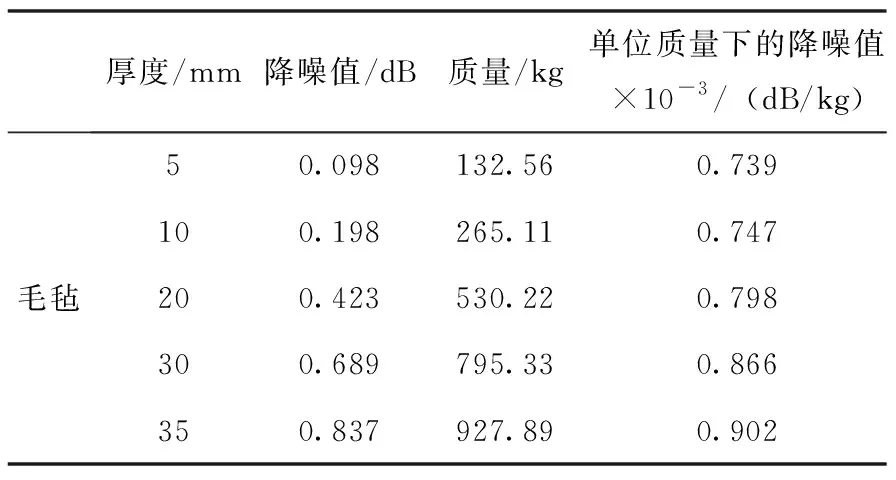
表5 單位質量毛氈的降噪值Tab.5 Noise reduction value of felt with per unit mass

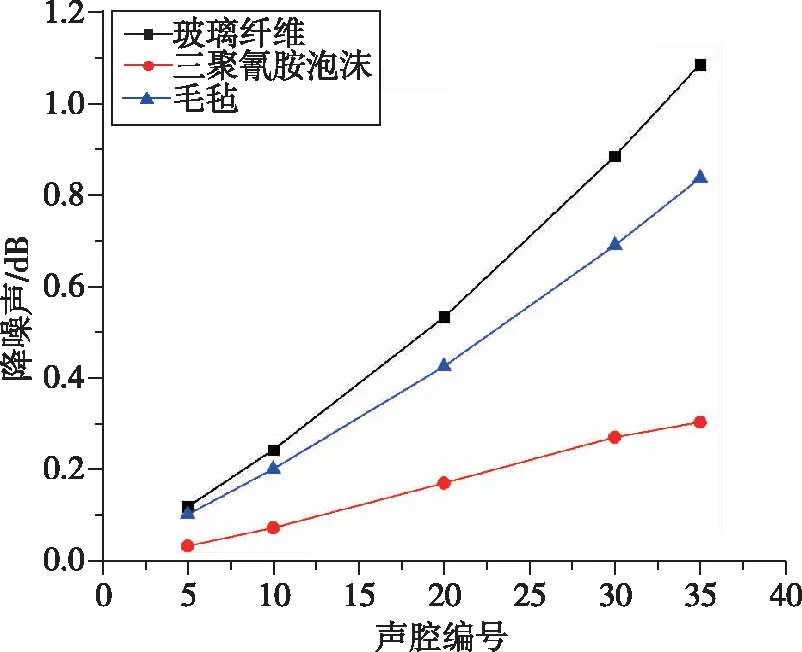
(a) 3種材料不同厚度下的降噪值

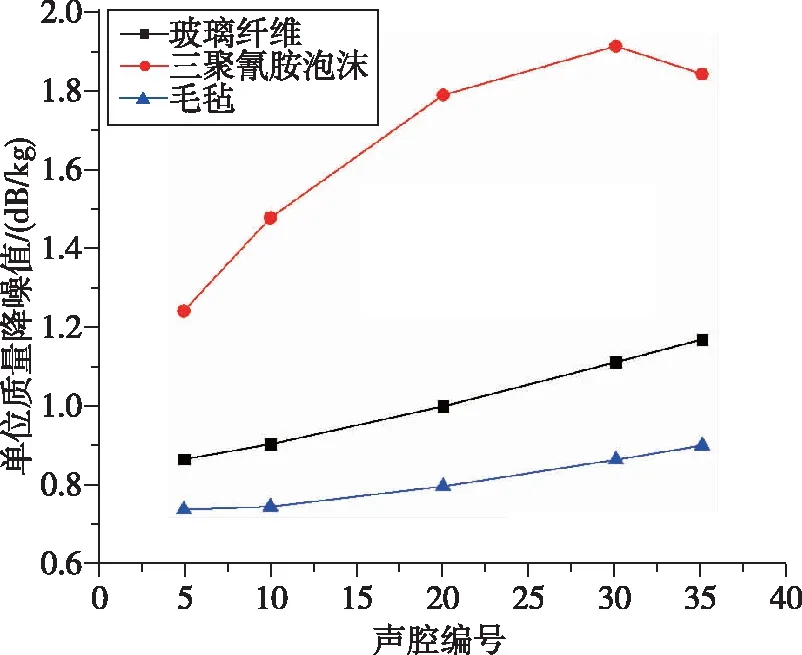
(b) 3種材料單位質量降噪值對比圖9 降噪材料在不同鋪設厚度下的降噪值及單位質量降噪值Fig.9 Noise reduction values and noise reduction values with per unit mass for different laying thicknesses of noise reduction materials

4 結論

本文基于SEA方法建立了考慮衛星結構的重型火箭整流罩噪聲響應分析模型，并通過在整流罩內壁鋪設降噪材料，分析各種降噪材料在不同參數下的降噪效果，具體工作和創新點如下：

1)相比于前人工作，本文提出了考慮衛星結構等負載對整流罩內噪聲響應的影響。考慮到衛星結構形式的復雜性，給建模帶來一定困難，因此將衛星結構簡化為圓柱或立方體的包絡形式，由此建立了重型火箭整流罩的SEA模型。

2)針對圓柱和立方體兩種不同的衛星包絡形式，分別采用控制變量法分析了衛星包絡結構高度和直徑(底面對角線長度)的變化對圓柱(錐)聲腔聲壓級的影響。圓柱形衛星包絡結構直徑和高度的增加有助于降低各圓柱(錐)聲腔的聲壓級，另外，隨著立方體形衛星包絡結構高度的增加，各圓柱(錐)聲腔的聲壓級呈降低的趨勢，但底面對角線長度變化對圓柱(錐)聲腔的聲壓級沒有明顯影響，以上結論可為后續整流罩內衛星的排布形式提供一些參考。

3)通過仿真分析玻璃纖維、毛氈和三聚氰胺泡沫在不同鋪設厚度下的降噪值和單位質量降噪值，可以發現在相同鋪設厚度下，三聚氰胺泡沫的降噪能力明顯弱于玻璃纖維和毛氈，但若考慮到降噪材料的質量約束時，三聚氰胺泡沫的單位質量降噪能力則明顯優于另外兩者。因此，在實際應用中不僅要滿足降噪要求，同時也要考慮降噪材料鋪設質量和厚度約束，以此通過鋪設單一降噪材料或多種降噪材料混合的方式獲得最優的鋪設方案。