基于神經網絡的矮塔斜拉橋近斷層地震響應參數敏感性分析*

王偉軍，虞廬松，王 力，李子奇,2，李健寧

(1.蘭州交通大學 土木工程學院，甘肅 蘭州 730070；2.蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，甘肅 蘭州 730070)

0 引言

近斷層地震動因其特有長周期速度脈沖，引起的結構地震響應較常規地震動更顯著[1-2]。隨著我國公路和鐵路網絡布局日益發達，部分橋梁因特殊原因須修建在斷層附近，這對橋梁的抗震設計提出更多挑戰。在美國加州，約5%的橋梁修建在跨越斷層斷裂帶或位于接近斷層破裂帶的地方[3]。矮塔斜拉橋因其“塔矮、梁剛、索集中”的特點，被廣泛應用于交通領域[4-5]。在橋梁抗震設計前需進行敏感性分析，以區分眾多設計參數對結構響應的影響程度。傳統的單因素敏感性分析方法計算量大且忽略設計參數之間的相互影響，局限性較大。蒙特卡洛法[6]、FITNET FFS模型法[7]、牛頓插值公式法[8]以及響應面法[9]為敏感性分析提供新思路。

隨人工智能發展，神經網絡因其“快速、精確、全面”的優點，被運用到敏感性分析中。針對近斷層地震動，學者通過反應譜分析指出，當前我國抗震規范的設計反應譜無法保證結構在近斷層區域的安全[10-11]；部分學者系統研究由方向性效應和滑沖效應引起的脈沖地震動對長周期結構的影響[12-13]。在矮塔斜拉橋抗震研究中：潘思璇等[14]研究行波效應對非對稱矮塔斜拉橋地震響應影響；王獻摯等[15]通過振動臺試驗發現主墩為矮塔斜拉橋主要損傷部位；Feng等[16]對地震作用下矮塔斜拉橋支座減震控制進行研究；崔春義等[17]對矮塔斜拉橋抗震性能進行系統評估，發現橋墩會發生較大的塑性變形。在神經網絡參數敏感性分析方面：Kourosh等[18]提出基于卷積神經網絡(CNN)的敏感性分析方法，并對其性能進行比較；Ghada等[19]使用深度殘差神經網絡對熱拌瀝青混合料進行參數敏感分析；Moussa等[20]在結構可靠度評估中引入神經網絡集成構建參數敏感性分析模型，驗證神經網絡在敏感性分析中的穩定性和準確性。

目前，針對橋梁參數敏感性在抗震方面的研究相對缺乏，對橋梁抗震設計和優化的參考不足。因此，本文提出基于BP神經網絡結合有限元(FEA)的參數敏感性分析(Sensitivity Analysis)方法(FBSA法)，計算矮塔斜拉橋地震響應參數敏感性，分析不同類型地震動(近斷層脈沖地震動、近斷層無脈沖地震動和遠場地震動)對矮塔斜拉橋地震響應參數敏感性的影響規律。研究結果可為近斷層橋梁抗震設計及優化提供依據。

1 基于神經網絡的敏感性分析方法

1.1 基于BP神經網絡的參數敏感性分析

3層BP神經網絡拓撲結構示意如圖1所示。由圖1可知，BP神經網絡由神經元組成網絡拓撲結構，所有神經元由輸入層、隱含層和輸出層組成，通過層間權值完成網絡連接，該權值通過誤差反向算法不斷更新，確保最終預測的準確性。每個神經元(隱含層和輸出層)中均包含1個輸入值和輸出值并通過激活函數連接。

圖1 3層神經網絡拓撲結構示意

響應對參數的偏導數即敏感性系數，量化了參數變化對響應的影響程度，激活函數選用S型函數，如式(1)所示：

(1)

式中：x表示神經元輸入；G(x)表示神經元輸出。

根據網絡結構可以得到隱含層第j個神經元的輸入tj和輸出hj，如式(2)所示：

(2)

同時，輸出層第k個神經元的輸入rk和輸出ok如式(3)所示：

(3)

式中：xi為輸入層神經元i的數值；wij為輸入層神經元i與隱含層神經元j的權值；vij為隱含層神經元j與輸出層神經元k的權值。

進一步得到輸出層神經元k的輸出值ok，如式(4)所示：

(4)

式(4)給出輸出與輸入之間的非線性表達式，是連續可微的。根據鏈式求導法則得到輸出值ok對于輸入值xi的偏導，如式(5)所示：

(5)

又激活函數滿足G′(x)=G(x)(1-G(x))，得到BP神經網絡中輸出響應對于輸入參數的敏感性系數，如式(6)所示：

(6)

當神經網絡確定，任一響應對于各輸入參數的敏感性系數均可求得。

1.2 樣本集獲取及數據歸一化

當輸入參數及其變化范圍確定后，采用正交試驗法對所選參數進行組合，并利用有限元分析獲取每組參數對應的響應，獲得神經網絡訓練樣本集。

為了加快收斂速度，避免參數上下限大小對訓練結果產生較大影響，在神經網絡訓練前需對輸入和輸出分別進行min-max歸一化，將數據歸一至[0,1]之間，如式(7)所示：

(7)

式中：x和X分別為歸一化前后值；xmax，xmin分別為樣本輸出或輸入中的最大值和最小值。

為分析方便且不失相關性，將式(7)得到的敏感性系數歸一化至[-1,1]，歸一化后的敏感性系數代表響應對于參數的敏感性程度(0表示參數對響應無影響)，如式(8)所示：

(8)

2 矮塔斜拉橋參數化數值模擬

2.1 工程簡介及設計參數選取

某鐵路大跨矮塔斜拉橋，跨徑布置(140+260+140) m，主梁為箱型截面，梁底按1.8次拋物線變化，采用C55混凝土，主塔為鉆石型結構，采用C45混凝土與主梁固結，與橋墩采用雙曲面鋼支座連接，橋墩為矩形墩采用C35混凝土，斜拉索呈雙索面扇形布置。矮塔斜拉橋幾何布置和截面尺寸示意如圖2所示。根據該橋特點，從幾何布置、截面尺寸和拉索參數3個方面選取設計參數，共計16種，具體設計參數類別及其變化范圍見表1。為保持原橋結構不變，除所選參數及與所選參數有比例關系的結構數據外，其余斜拉橋參數保持原橋值。根據參數變化范圍，每個參數確定5個變量值并進行正交設計，共組成57組參數樣本。

表1 設計參數類別及變化范圍

圖2 矮塔斜拉橋幾何布置及截面尺寸示意

2.2 有限元模型建立及其參數化

基于ANSYS通用有限元分析軟件，利用參數化程序設計語言(APDL)建立全橋三維有限元模型，并考慮斜拉橋幾何非線性效應，如圖3所示。

圖3 矮塔斜拉橋有限元模型

主梁采用“脊梁式”建模，建立剛性橫梁與拉索連接，主梁節點處設置質量單元模擬主梁自重，對墩底進行固結處理。利用APDL命令與Python語言交互完成有限元模型參數化，通過Python的OS模塊依次將上述57組參數樣本寫入ANSYS，進行自動運算并導出計算結果，得到57組參數樣本對應響應樣本，組成神經網絡訓練的樣本集。

2.3 動力特性

矮塔斜拉橋前10階振型見表2。1階主梁對稱側彎早于1階主梁豎彎出現，主梁縱飄和1階主塔同向側彎分別發生在第4，10階振型。

表2 矮塔斜拉橋動力特性

3 近斷層地震動選取

橋址所在地抗震設防烈度為Ⅶ度，基本地面加速度為0.17g，場地特征周期0.45 s。按照斷層距和有無脈沖信號分別選取近斷層脈沖地震動、近斷層無脈沖地震動和遠場地震動各3條，取每類3條地震非線性時程分析結果最大值作為該類地震動作用下的地震響應，地震波信息及分類見表3。地震動水平正交輸入，峰值加速度調至0.3g。

表3 地震動信息及分類

4 近斷層地震動地震響應分析

4.1 塔墩響應

在不同類型地震動作用下主塔主墩沿高度方向上內力和位移峰值包絡圖如圖4所示。由圖4(a)～(b)可知，主塔和主墩的縱、橫向位移峰值均發生在塔頂和墩頂；脈沖地震動下，主塔和主墩變形較遠場地震動明顯增大，縱向位移增幅大于40%，而橫向位移增幅最大超過1倍；無脈沖型地震動和遠場地震動下，塔墩橫向和縱向位移差距小于20%。由圖4(c)～(d)可知，主墩峰值內力發生在墩底位置，而主塔內力峰值在塔底向上約15 m處，該處正好為主梁頂面位置，由于塔梁固結，使內力和峰值位移發生偏移。無脈沖地震動和遠場地震動作用下，橋塔和橋墩內力區別較小。除對橋塔剪力以外，與遠場地震相比，脈沖地震動對于塔墩內力的增幅約為110%。

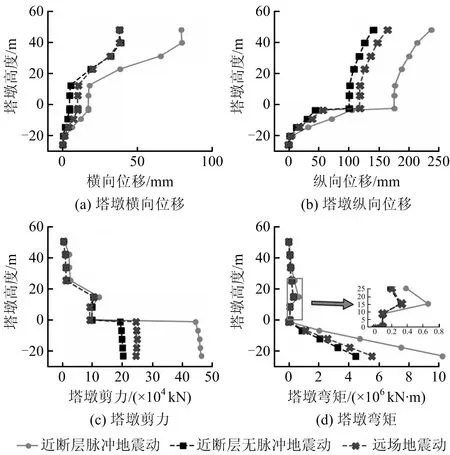
圖4 塔墩地震響應

4.2 主梁響應

各地震動作用下主梁位移峰值包絡圖如圖5所示。由圖5可知，主梁橫向和豎向峰值位移位于中跨跨中位置。在遠場地震動和無脈沖地震動下橫向位移和豎向位移差異不明顯，脈沖地震動對主梁橫向位移的增幅較大，而對豎向位移增幅不明顯。

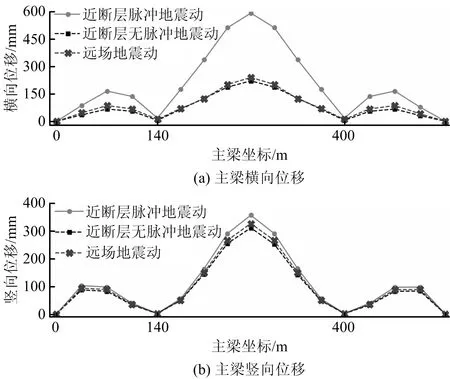
圖5 主梁地震響應

依據上述分析，本文取矮塔斜拉橋主塔、主墩和主梁響應最大值位置為相應地震響應控制點。

5 近斷層地震響應參數敏感性分析

5.1 自振頻率參數敏感性分析

由于篇幅原因，本文僅對結構影響重要的1階主梁側彎、豎彎、縱飄和橋塔側彎的第1，2，4，10階頻率進行參數敏感性分析，結果見表4。

表4 自振頻率敏感性分析

由表4可知，主梁側彎受DV4、DV1、DV2、DV8和DV13影響較大；DV7，DV13對主梁豎向變形影響較大；DV4，DV5，DV7對主梁縱飄有較大影響，說明幾何布置是主梁的振型剛度的決定性因素。對于主塔側彎，DV12，DV3，DV5，DV1，DV11，DV9對其影響較大，表明除變化主塔截面尺寸，還可通過幾何布置和主梁截面的改變調整主塔振型剛度。綜上，幾何布置和截面尺寸對矮塔斜拉橋抗震性能影響很大。

5.2 主塔地震響應參數敏感性分析

主塔在不同類型地震動作用下，各設計參數對于地震響應的敏感性系數雷達圖如圖6所示。

圖6 T1橋塔地震響應敏感性

由圖6(a)可知，在各類地震動作用下DV3，DV10，DV12，DV14，DV16對橋塔橫向位移響應影響較大，敏感性系數絕對值均大于0.5。近斷層脈沖地震動下DV5，DV6對主塔橫向位移影響較大，敏感性系數分別為0.89，-0.48，遠大于其它2類地震動作用。由圖6(b)可知，DV3，DV8在各類地震動作用下都對主塔縱向位移產生較大影響，敏感性系數絕對值皆均大于0.5。而相較于其它地震動，近斷層脈沖地震動使主塔縱向位移對DV6，DV11，DV15，DV16更為敏感。

由圖6(c)～圖6(d)可知，塔底剪力與彎矩在地震荷載作用下各參數對其影響規律一致；在各類地震動作用下，敏感性系數差異不明顯。主塔內力DV8，DV11，DV13最為敏感，敏感性系數絕對值介于0.7～1.0；DV2，DV3，DV5，DV9對其影響次之。

5.3 主墩地震響應參數敏感性分析

主墩在不同類型地震動作用下，各設計參數對于地震響應的敏感性系數如圖7所示。由圖7(a)可知，在不同地震動作用下墩頂橫向位移受DV5，DV6，DV7，DV9，DV11影響均顯著。在近斷層脈沖地震動下DV10，DV12，DV13，DV14對主墩橫向位移的敏感程度較其他地震動更高，說明近斷層脈沖效應使得主墩橫向位移與結構截面剛度聯系更加密切。近斷層脈沖地震動下DV8對橫向位移的敏感性值趨于0，說明脈沖效應會削弱原本敏感性較大參數對響應的影響。由圖7(b)可知，在各類地震作用下DV5，DV11，DV15對橋墩縱向位移的影響較大，并且其余2類地震動曲線幾乎被近斷層脈沖地震動曲線包絡，說明近斷層脈沖效應可以較大程度地激活主墩縱向位移對各設計參數的敏感性。

圖7 ZP2橋墩地震響應敏感性

由圖7(c)～圖7(d)可知，橋墩彎矩與剪力受參數影響的敏感性規律趨于一致，但在不同類型地震動下，敏感性出現較大差異。DV5，DV14對橋墩內力影響都很敏感，敏感性系數絕對值均大于0.7。近斷層地震動(脈沖型和無脈沖型)作用下，橋墩內力對于DV1，DV2，DV7，DV8的敏感性較遠場地震動明顯增大，說明近斷層地震動可以激發橋墩內力對于參數的敏感程度，且這種增大效果與近斷層脈沖效應無關。

5.4 主梁響應參數敏感性分析

在各類地震動作用下主梁地震響應敏感性如圖8所示。由圖8(a)可知，近斷層無脈沖地震動和遠場地震動作用下敏感性曲線分布規律基本一致；在近斷層脈沖地震動下DV4，DV8，DV11，DV13主梁橫向位移的敏感性系數值大幅增加，脈沖效應使其變化明顯。由圖8(b)可知，近斷層特性對主梁豎向位移參數敏感性的影響較小。在地震動作用下DV2，DV4，DV8，DV11，DV13對主梁豎向位移的敏感性系數絕對值均大于0.5。

圖8 主梁地震響應敏感性

6 結論

1)結合BP神經網絡與有限元的參數敏感性分析方法(FBSA法)，可充分考慮橋梁各參數間的相互影響，更符合橋梁抗震設計與優化的需求。

2)近斷層地震動對矮塔斜拉橋的塔墩縱向位移響應影響大于40%，塔墩橫向位移、塔墩內力、主梁橫向位移響應的增幅均大于1倍，但對其豎向位移影響并不明顯。

3)同一參數對矮塔斜拉橋不同地震反應的敏感程度不同，在抗震設計中應根據橋梁易損部位的響應控制目標確定設計參數的重要性；塔墩剪力和彎矩受設計參數敏感規律一致；振型剛度對橋梁幾何布局和截面尺寸的敏感性較強。

4)近斷層脈沖地震動對矮塔斜拉橋的橋塔位移、橋墩位移和內力以及主梁橫向位移的參數敏感性影響較大，而主塔剪力、主塔彎矩和主梁豎向位移參數敏感性在近斷層地震動下影響不顯著。