四電平浮動交錯Boost DC/DC 變換器研究

安江偉

（河南理工大學電氣工程與自動化學院,河南 焦作 454000）

單體燃料電池電壓一般低于1 V,需要將單體電池堆疊成燃料電池堆,這勢必導致燃料電池堆體積和重量增大.車載燃料電池體積一般不大,輸出電壓較低,不能直接驅動汽車電機,需要在燃料電池和逆變器直流母線之間添加合適的DC/DC 變換器,將燃料電池電壓升到合適的電壓等級[1-3].

DC/DC 變換器可以分為隔離型和非隔離型.非隔離型DC/DC 變換器主要包括:buck 變換器、boost變換器、buck-boost 變換器、cuk 變換器、sepic 變換器、zate 變換器[4].通過在非隔離型變換器的拓撲結構中加入變壓器并進行改進可以得到隔離型DC/DC 拓撲結構,主要有正激式、反激式、推挽式以及橋式四類[5-8].但隔離型DC/DC 變換器拓撲中引入了變壓器,故而體積大、成本高.目前,具有結構簡單、控制容易等優點的非隔離型DC/DC 變換器廣泛應用在燃料電池汽車中.為了獲得高增益的變換器拓撲,目前主要采用的方法有三種,分別為級聯型[9-12]、耦合電感型[13-15]、開關電容型[16].DC/DC 變換器根據電平數不同可以分為兩電平和多電平結構.兩電平DC/DC 變換器的開關管電壓應力大.DC/DC 變換器工作在高電壓大容量場合,需要具有電流紋波小、電壓應力小、諧波失真小等優點,三電平和多電平符合上述要求.文獻[17]提出將兩個boost 三電平變換器并聯,不具有高增益的特性.文獻[18]提出懸浮交錯boost 變換器方案,其具有高增益特性,但該變換器開關管承受的電壓應力較大.

為此,本文針對四電平DC/DC 變換器升壓比低的問題,提出了四電平懸浮交錯boost DC/DC 變換器（Four-level Floating-output Interleaved-input Boost DC/DC Converter,FL-FIBC）,并對其拓撲結構及其工作原理進行分析研究,針對非交錯調制方式下輸出電壓紋波大的情況,采用交錯調制方式;針對DC/DC變換器的強非線性、強耦合特性,設計了模糊PI 控制策略.將模糊控制算法與PI 控制相結合,通過設計模糊控制規則,實現了對PI 參數的實時整定.通過在MATLAB 中搭建仿真,驗證了所設計控制器的有效性.

1 FL-FIBC 拓撲結構

FL-FIBC 拓撲結構如圖1 所示,由兩個四電平boost 變換器模塊交錯并聯構成,形成了輸入輸出不共地的拓撲結構.其中,Q1~Q6為開關管,L1、L2為升壓電感,D1~D6為二極管,Vin為輸入電壓源,Cf1、Cf2為前級飛跨電容,C1、C3為后級飛跨電容,C2、C4為后級電容,R 為負載,Vout為直流母線側電壓.

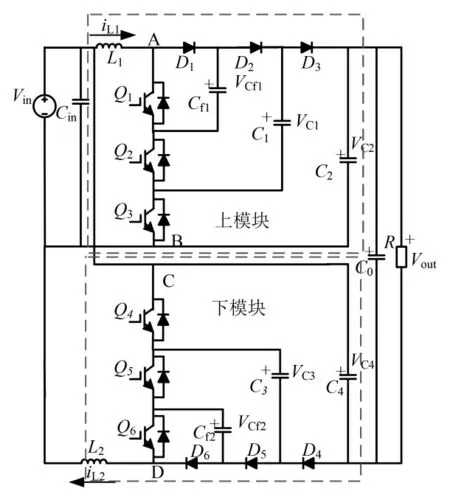
圖1 FL-FIBC 拓撲結構Fig.1 FL-FIBC converter topology

由圖1 可得FL-FIBC 的輸入輸出關系為,輸出電壓為兩模塊電容電壓的和減去輸入電壓,即

式（1）中:VC2、VC4分別為后級電容C2、C4端電壓.

假設變換器工作在理想情況下,對稱點的器件參數相等.由伏秒平衡原理得出變換器的電壓增益,也即電感L1 在一個周期內充放電電荷相等,可得FL-FIBC 輸入輸出電壓關系,如下表達式

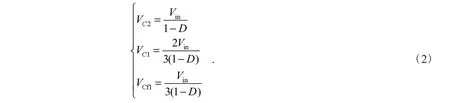
由上下模塊的對稱關系可得

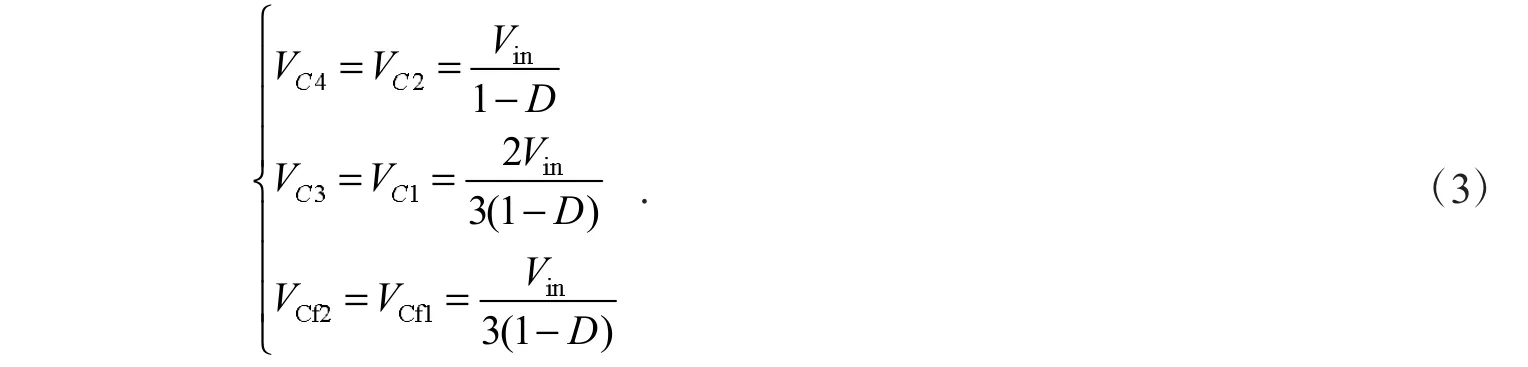
在理想情況下,即前級飛跨電容電壓相等,即式（3）,聯立式（1）、（3）可得

式（4）中:VCf1、VCf2分別表示上下模塊的前級飛跨電容電壓,VC1、VC3表示上下模塊的后級飛跨電容電壓.

將式（3）中的參數代入式（1）可得電壓增益為

故輸入電流Iin和輸出電流Iout的關系為

由式（5）可知,FL-FIBC 的升壓比為（1+D）/（1-D）.相較四電平boost DC/DC 變換器的電壓增益升高,與TL-FIBC 相比,其開關的電壓應力降低,為Vin/[3（1+D）].為此表1 中分析了四種拓撲結構中開關管的電壓應力、增益、電流應力.

表1 四種拓撲開關管應力及增益對比Tab.1 Comparison of stress and gain of four topology switches

由表1 可知,FL-FIBC 相對于普通的兩電平boost 變換器而言, 開關管的電壓電流應力及增益均有較大提高.另外,FL-FIBC 和TL-FIBC 的電壓增益相等,但FL-FIBC 的開關管電壓應力較低.

以上分析可知,FL-FIBC 具有高增益特性;開關管電壓應力為輸入電壓和輸出電壓和的六分之一;結構簡單,輸入輸出不共地;變換器的各部分電壓電流紋波相對較小.

2 工作原理分析

假設變換器工作在連續電流模式（CCM）,正常工作時各個電容電壓滿足式（3）.定義開關管導通為1,開關管關斷為0.其開關管Q1、Q2、Q3的導通時間定義為占空比Dn（n=1,2,3）,用開關管Q1、Q2、Q3的導通、關斷狀態描述四電平boost 變換器的工作情況.其工作模態可以根據開關管Q1、Q2、Q3占空比的大小分為三種開關模式,令三個開關管的占空比相等,即D1=D2=D3=D,這些模式通過三個控制信號的和來表示,分別為0≤D<1/3、1/3≤D<2/3、2/3≤D<1.其子模塊的工作情況如表2 所示.

表2 子模塊工作情況Tab.2 Sub module operation

由表2 可知,子模塊在一個開關周期內存在四個電平,分別為VC2、VC1、VCf1、0.

四電平boost 變換器的電壓電流波形如圖2 所示,其中包括Q1、Q2、Q3的驅動波形,電感電流iL1的波形和AB 兩點的電壓波形.圖2-a 為變換器在開關模式1 時的工作特性,圖2-b 為變換器在開關模式2時的工作特性,圖2-c 為變換器在模式3 時的工作特性.

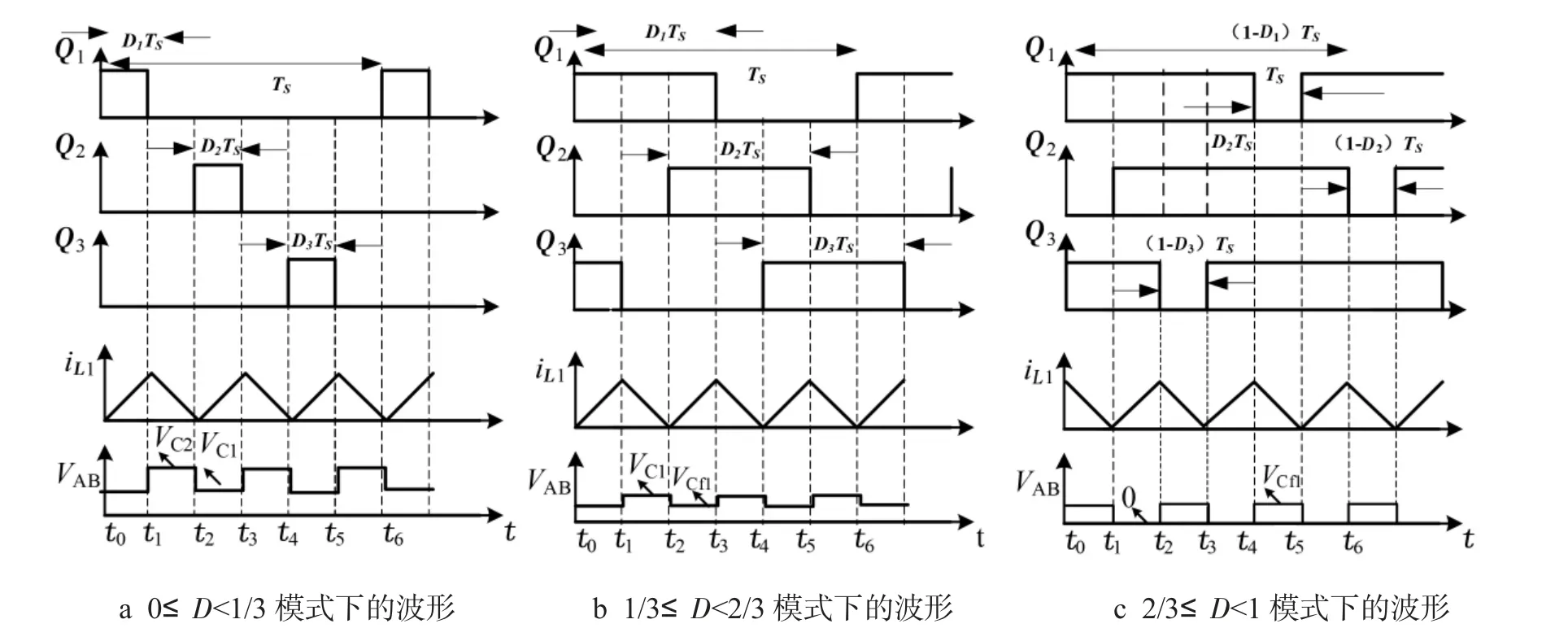
圖2 boost 四電平變換器主要波形Fig.2 Main waveforms of Boost four-level converter

從圖2-a 中可以看出,開關管不會同時導通,但是在圖2-b、圖2-c 中會出現開關管同時導通的工作情況.從圖中還可以看出,變換器電感電流的脈動頻率是開關管脈動頻率的兩倍.針對這一特征,當電感的脈動頻率增加時,在其它條件不變的情況下,可以適當減小電感量,縮小電感所需要的成本.另外,當變換器工作在情況1 時,變換器只有四種開關模態:S0=000、S1=001、S2=010、S4=100,而不存在兩個開關管同時導通的情況;當變換器工作在情況2 或3 時,其開關模態為:S3=011、S5=101、S6=110、S7=111.

3 調制策略

FL-FIBC 有6 個開關管要驅動,且每個開關管的導通時間相同,器件Q1~Q3、D1~D3構成上模塊,器件Q4~Q6、D4~D6構成下模塊.同一模塊的開關管的驅動信號移相120°,上下模塊開關管的導通相位不同導致電容電感充放電順序不同,采用相位交錯導通方式可以降低電壓紋波.以此根據開關管的相位關系,將電路分為非交錯調制方式與交錯調制90°導通方式,具體調制方式如表3-1 所示.兩個模塊形成懸浮交錯的關系,子模塊的工作原理與四電平boost 變換器相同.

表3 調制方式表Tab.3 Modulation method table

交錯調制方式為模塊對稱點的開關管導通相位相等,通過分析可知,上下模塊對稱點開關信號交錯導通,采用此種方式能夠有效降低輸出電壓紋波,提高電能質量.其中導通方式的工作波形如圖3 所示.非交錯模式和四電平boost 變換器的工作波形相同,如圖2 所示.

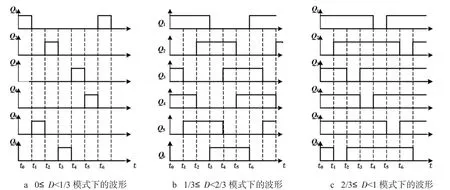
圖3 FL-FIBC 主要波形Fig.3 Main waveform of FL-FIBC

圖3 中Q1~Q6表示FL-FIBC 開關管驅動信號.FL-FIBC 變換器采用交錯調制時,其輸出電流由兩個模塊的升壓電感波形疊加而成.對稱點模塊的開關管的驅動信號交錯90°,且上下模塊對稱,其兩升壓電感的充放電時間相同,電流的上升和下降斜率也一樣,iL1、iL2的增大和減小會形成互補狀態.疊加的電流呈現零紋波輸出,有效降低了輸出電流紋波.

4 控制策略分析

FL-FIBC 具有非線性、時變的特性,難以建立變換器的精確數學模型,故傳統的線性控制難以獲得預期的效果.因此,將PI 控制與模糊理論相結合,其中電壓外環采用模糊PI 控制,電流內環采用PI 控制.采用模糊PI 控制,當系統工況發生變化時,參數具有自適應調整能力,提高了系統的動態性能.模糊控制器是由模糊化、知識庫、模糊推理和清晰化四部分組成,基本結構如圖4 所示.

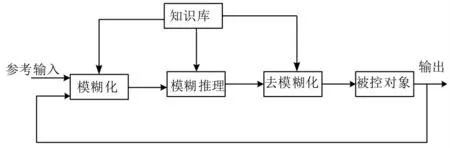
圖4 模糊控制器的結構Fig.4 Structure of fuzzy controller

模糊PI 控制器的工作流程為,首先采樣輸出電壓并與參考電壓對比得到輸出的偏差e 和偏差變化率ec,經模糊控制器后輸出ΔKP、ΔKi然后與kp、ki相加,改變參數以適應被控對象特性的變化,在此仿真中采用二維的Mamdani.通過模糊規則對PID 的三個參數進行實時地調整,以達到對不同時刻的PID參數進行自整定的目的,其結構如圖5 所示.

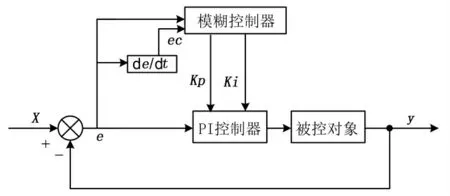
圖5 模糊PI 控制結構Fig.5 Fuzzy PI control structure diagram

模糊控制器是模糊PID 控制器的關鍵,模糊控制器先把輸入變量的清晰值經過量化因子變為模糊值,以方便模糊推理機進行推理.模糊化模塊設計:精確量的模糊化、模糊規則庫的制定、模糊推理、解模糊化.

（1）輸入輸出變量的模糊化.本文選擇清晰量e 和ec,PI 控制器中的參數ΔKP、ΔKi進行轉換,使其變換到各自的論域范圍.e 和ec 經過模糊化處理后得到的模糊化變量為E、EC.取e 和ec 的論域范圍（-3,3）,kp、ki的論域分別為（-1,1）、（-60,60）,取七個模糊子集,語言變量值取為{NB NM NS ZO PS PM PB},分別表示{負大負中負小零 正小正中正大}.利用MATLAB Fuzzy 工具箱作出e、ec、kp、ki的論域和語言變量.中間選用三角函數作為系統的隸屬度函數.NB 和PB 的隸屬度函數分別選用Z 型和S 型.

（2）模糊規則庫的設計.模糊控制的核心是建立模糊規則.根據PI 調節的比例環節、積分環節的調整過程,通過檢測每個時刻的系統輸出e 和ec 的大小,根據模糊規則得出PI 控制器參數的修正量,在線整定控制系統中的兩個參數kp、ki,對PI 在不同工況下的自整定應滿足以下規則:

1）誤差|e|較大時,kp值應較大,ki值應盡可能小,這可以減少響應時間和超調量;

2）誤差|e|中等時,為減小超調量,kp應當減小.為了系統的響應速度,ki取中等值;

3）誤差|e|較小時,為避免在設定值附近震蕩,ki應當增大,同時kp減小.

通過上述規則,建立的模糊規則如表4 所示.

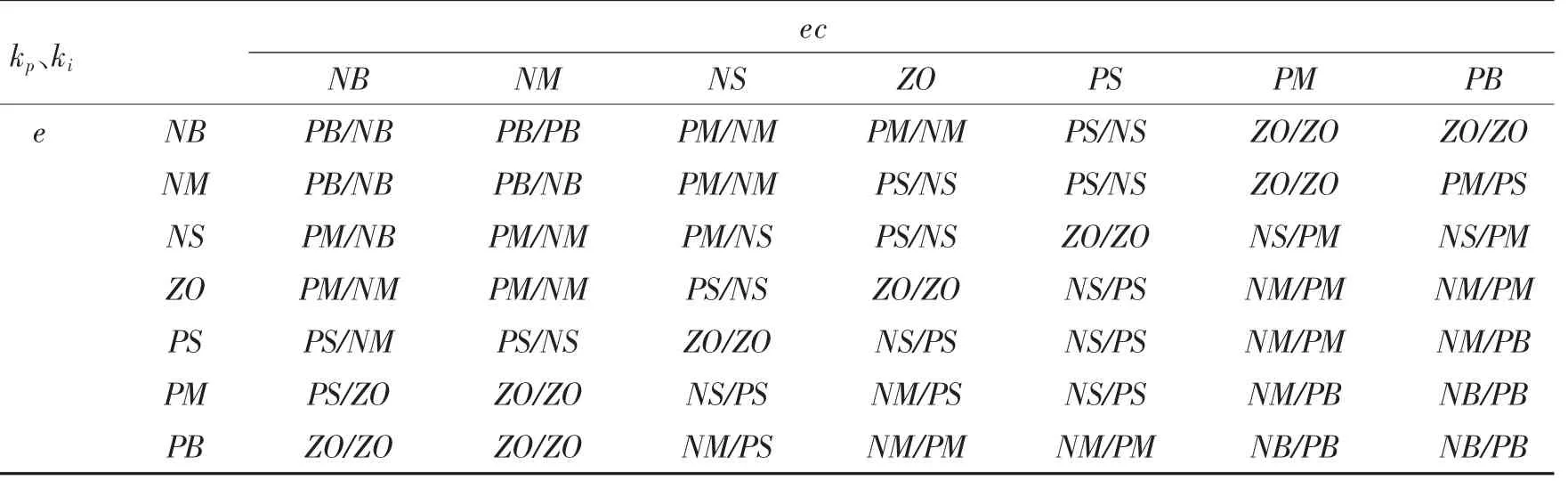
表4 kp、ki 模糊控制規則表Tab.4 kp、ki Fuzzy control rule table

（3）模糊推理和解模糊化.模糊推理是根據專家經驗等已經指定好的一組模糊規則,并根據該規則進行模糊邏輯推理.

通常使用IF…then…條件語句進行表達,總共有49 條規則,如:

1）、IF（e is NB）and（ec is NB）then（is PB）and（is NB）;

2）、IF（e is NB）and（ec is NM）then（is PB）and（is PB）;

┆

49）、IF（e is PB）and（ec is PB）then（is NB）and（is PB）.

以上通過模糊推理得到的結果仍然是模糊量,需要進行解模糊化處理.本文采用重心法.

5 電路仿真與分析

為了驗證FL-FIBC 的穩態特性,在MATLAB/Simulink 中搭建仿真模型.設計輸入電壓Vin=100 V,輸出電壓Vout=700 V,設計電容電壓紋波系數為1%、電感電流紋波系數為10%,開關頻率fs為50 KHz.參數選型如表5 所示.

表5 變換器仿真參數Tab.5 Converter simulation parameters

5.1 不同調制方式下穩態性能對比分析

為了驗證FL-FIBC 參數設計的正確性及其穩態特性,對變換器的穩態特性進行仿真,仿真后得到變換器電壓電流波形如下所示.

圖6、圖7 分別為變換器運行在非交錯調制與交錯調制方式下各參數波形.

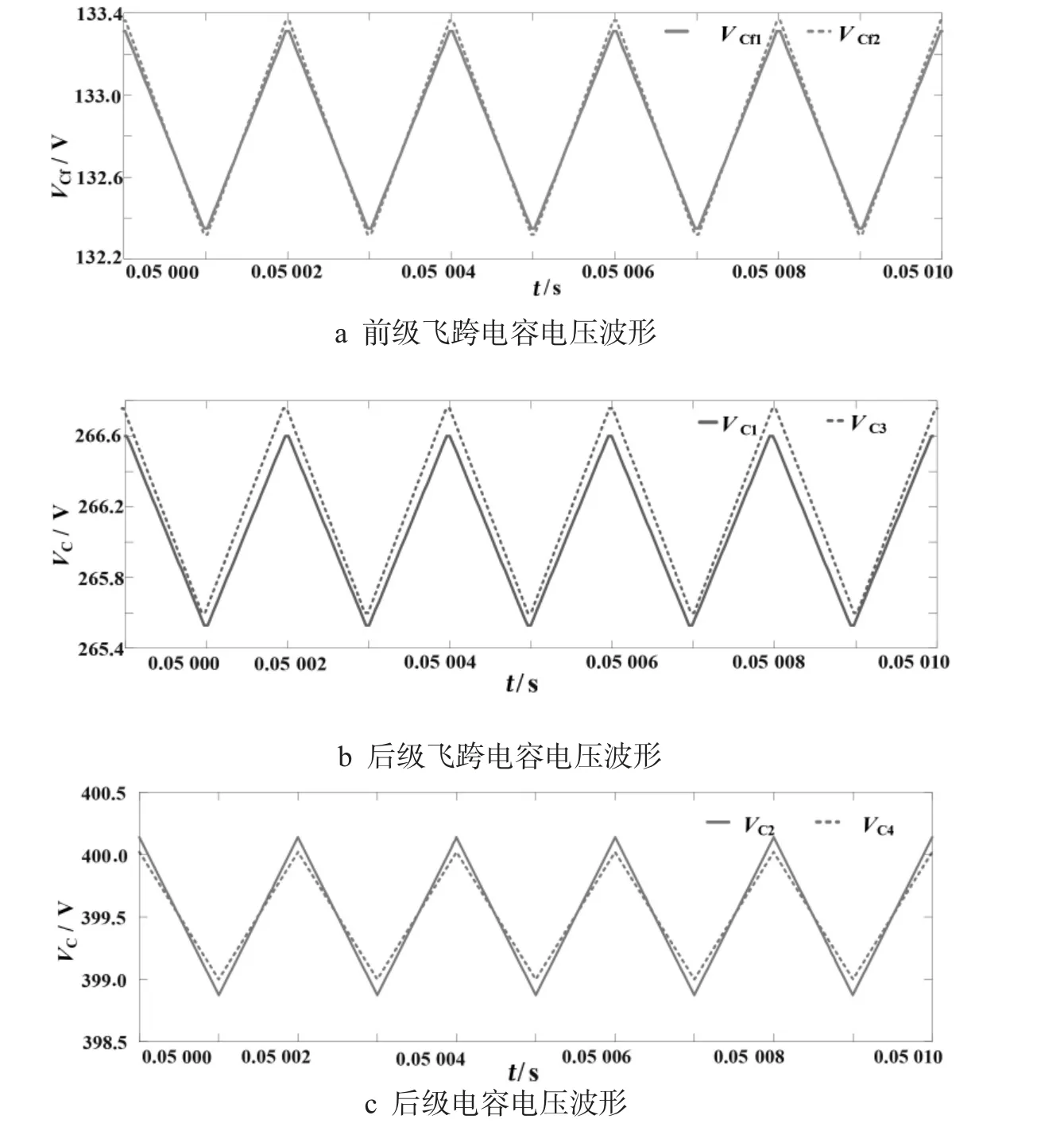
圖6 非交錯調制方式下各個電容電壓波形Fig.6 Voltage waveform of each capacitor under non interleaving modulation mode

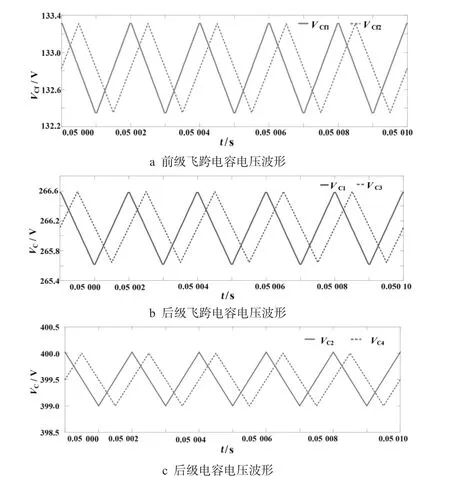
圖7 交錯調制方式下各個電容電壓波形Fig.7 Voltage waveform of each capacitor under non interleaving modulation mode

圖6 表示的是非交錯調制下的電容電壓波形,圖7 表示的是交錯調制下的電容電壓波形.在兩種調制方式下前級飛跨電容電壓VCf1、VCf2穩定在133.33 V,后級飛跨電容電壓VC1、VC3穩定在266.67 V,后級電容電壓VC2、VC4穩定在400 V,分析可知,當變換器工作在交錯調制方式下,其各個電容電壓的紋波相較非交錯調制方式下小.

圖8 為兩個升壓電感電流及疊加后波形.當采用交錯調制時,疊加后的電流紋波降低.

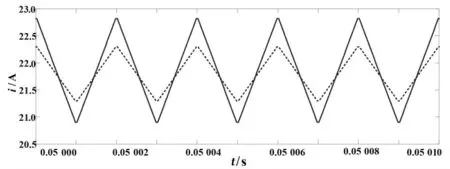
圖8 非交錯與交錯調制下電感電流波形Fig.8 Inductor current waveform under non interleaving and interleaving modulation

圖9 為輸出電壓波形,其中實線表示非交錯調制方式,虛線代表交錯調制方式.從圖可以看出,兩種調制方式下輸出電壓穩定在700 V.其中,在非交錯調制方式下,Vout紋波電壓約為4 V;在交錯調制方式下,Vout紋波電壓約為2 V.當電路工作在交錯調制方式下,輸出電壓紋波得到了改善.

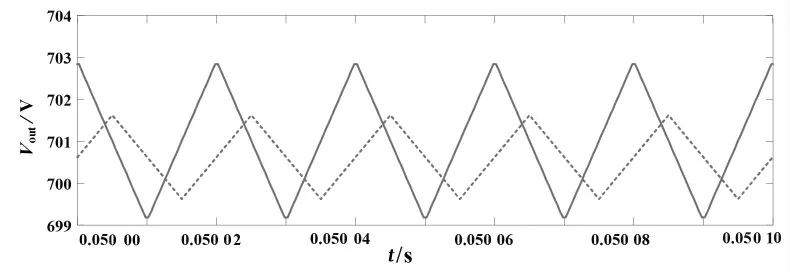
圖9 非交錯與交錯調制下輸出電壓波形Fig.9 Output voltage waveform under non interleaving and interleaving modulation

當電路工作在交錯調制方式時,為了驗證所設計控制策略的有效性及變換器系統的穩定性,對變換器進行仿真測試.

5.2 模糊PI 仿真分析

在MATLAB/Simulink 中搭建仿真模型驗證模糊PI 控制策略的正確性.

圖10 為穩態下變換器的輸出電壓波形圖.

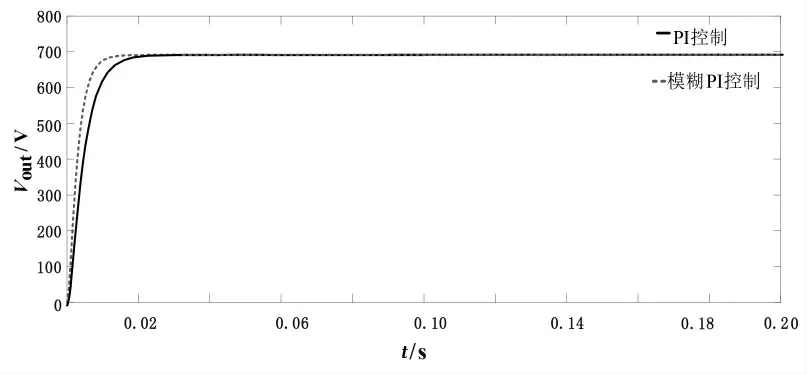
圖10 輸出電壓波形Fig.10 Output voltage waveform

由圖10 可以看出,當系統控制器采用模糊PI 控制時,變換器的動態響應要優于PI 控制,提升了系統的動態性能.圖11 為對變換器作負載突變與輸入電壓突變時變換器的輸出響應.

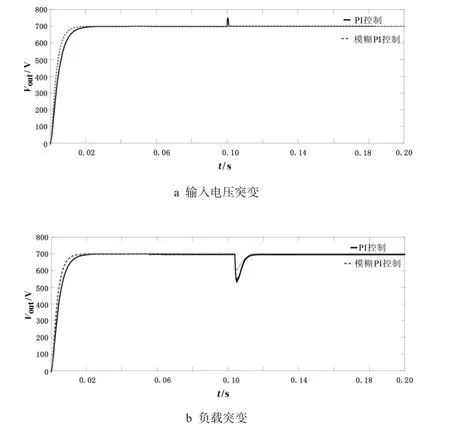
圖11 各擾動下輸出電壓波形Fig.11 Output voltage waveform under each disturbance

圖11-a 為0.1 s 時輸入側電壓突變至400 V 時的輸出電壓波形.由圖中可以看出,當系統控制器采用模糊PI 控制時,輸出電壓的波動值要小于PI 控制.圖11-b 為0.1 s 時輸出側并聯200 Ω 電阻后的輸出電壓波形.由圖中可以看出,當系統控制器采用模糊PI 控制時,輸出電壓的跌落值要小于PI 控制.

由上述分析及仿真可知,當變換器采用模糊PI 控制時,系統的動態響應要由于PI 控制,提升了系統的動態性能.

6 小結

本文提出了FL-FIBC 高增益電路拓撲,開關管的電壓應力降低,通過分析變換器不同調制方式下的穩態性能,得出了交錯調制方式下,電流紋波降低.針對變換器的非線性、強耦合特性,設計了模糊PI 控制策略,實現了對PI 參數的實時整定.通過在MATLAB/Simulink 中搭建仿真,驗證了當變換器工作在模糊PI 控制策略時,系統的動態性能得到了提升.因此,FL-FIBC 不僅具有高增益的特性,而且當其采用模糊PI 控制算法時,能夠實現系統更好的控制性能.