基于馬爾科夫鏈-多目標模型的應急供應鏈決策優化研究*
陳偉炯,董雯玉,李咪靜,張善杰,李曉戀,,康與濤
(1.上海海事大學 物流科學與工程研究院,上海 201306;2.上海海事大學 物流供應鏈風險控制研究中心,上海 201306;3.上海海事大學 海洋科學與工程學院,上海 201306)
0 引言
突發災難事件頻發,嚴重影響人類生活、社會穩定和經濟發展。國家應急管理部數據顯示,2020年我國自然災害以地質災害、洪澇為主,全年受災人群達1.38億人,死亡及失蹤人數共591人,造成直接經濟損失3 701.5億元[1]。2020年新冠疫情曾造成口罩、防護服等相關應急醫療物資短缺,嚴重威脅公眾生命安全。應急救援亟待低風險、高效率的應急供應鏈。
目前,應急供應鏈風險分析與應急物資優化調度成為國內外研究熱點。在應急供應鏈風險分析方面,研究趨勢逐漸由靜態向動態轉變,動態研究能夠更加真實、客觀地反應供應鏈風險及其變化。一方面,學者基于馬爾可夫過程、混合數學規劃、動態貝葉斯網絡、魯棒控制優化等[2-4]方法構建動態應急供應鏈模型,在災情更新情況下分析供應鏈中的潛在風險,為應急管理提供實時有效的政策調整建議。另一方面,單一目標的應急物資調度規劃模型已無法滿足應急管理實際需求,因此,部分學者聚焦于多目標規劃模型的研究,包括以最小化延遲時間、最小化運輸成本或系統損失的雙目標規劃模型[5-6],在此基礎上考慮最大化線路可靠性[7]、最大化供應鏈可視性[8]、最小化物資短缺[9]等因素的3目標優化模型。為有效提高應急供應鏈中斷響應效率,學者展開應急供應鏈決策優化研究,基于可持續性、魯棒性、韌性等,設計優化應急組織配置策略[10]、協同優化方法[11]、韌性優化策略[12],增強應急供應鏈恢復力,高效地應對風險,降低災害損失。
在應急供應鏈風險動態變化基礎上,現有研究對應急物資的多目標規劃與決策優化的綜合性研究尚有不足,且在算法求解上仍有改進空間。因此,本文提出離散時間馬爾科夫鏈—多目標規劃模型(DTMC-MOP),綜合考慮供應率、時間、成本3個因素,動態識別、分析、應對應急供應鏈風險,并采用改進自適應NSGA-Ⅱ算法優化求解模型,以實現應急物資的最大滿足率供應、最短時間供應和最低成本供應目標,研究結果可為及時控制災情和最大限度地降低災害損失提供參考。
1 DTMC-MOP應急供應鏈模型的構建
突發災難事件發生時,應急供應鏈易受內外部不同程度的風險擾動。為保障應急救援工作的順利開展,構建由應急管理部門、供應商、制造商、需求方組成的4級動態應急供應鏈網絡,基于離散時間馬爾科夫鏈(DTMC)模型,將狀態轉移概率及平穩概率分布引入多目標規劃(MOP)模型,構建供應物資滿足率最大、供應時間最短、供應成本最低的DTMC-MOP模型。
1.1 基于離散時間馬爾科夫鏈的應急供應鏈模型
1)定義
①離散時間馬爾科夫鏈
若隨機序列{Xn,n=0,1,2,…}為狀態離散的隨機過程,其中狀態空間I={i0,i1,…,in,j},時間集合T={0,1,2,…},如果對于任意狀態滿足式(1):
(1)
則稱{Xn,n=0,1,2,…}是離散時間馬爾科夫鏈[13]。
②k步轉移概率及矩陣如式(2)所示:
(2)
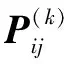
(3)
③平穩概率分布
若分布概率π=(π1,π2,…,πj)滿足式(4):
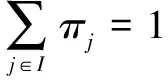
(4)
則稱分布概率π是{Xn}的唯一平穩概率分布。
2)DTMC應急供應鏈模型
突發災難事件是1個隨機過程,且應急供應鏈的下一種狀態僅和當前狀態有關,具有馬爾科夫性。通過DTMC模型動態描述應急供應鏈所處狀態,直觀反映應急供應鏈的運行狀況。
考慮到供應鏈的韌性特征,即受到風險擾動導致供應鏈部分失效時仍能維持供應狀態,并以最快的速度恢復到正常供應狀態的能力。假設應急供應鏈在t時刻處于受不同程度干擾的有限個離散狀態,由于供應鏈具有韌性,在t+1時刻可以向其他狀態轉移或保持該狀態不變。當發生風險擾動時,假設應急供應鏈存在以下4種狀態:狀態0即完全吸收干擾的正常供應狀態;狀態1~3分別表示受到30%,60%,90%干擾的供應狀態。任意2個狀態之間可相互轉移,用α1~α6和β1~β6(αi,βi≤1,i=1,…,6)表示狀態轉移概率。應急供應鏈DTMC模型如圖1所示。
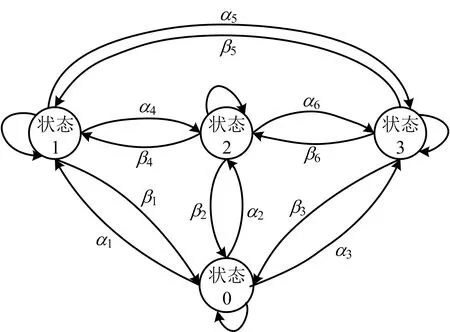
圖1 應急供應鏈的DTMC模型
由圖1可知,若t時刻供應鏈處于狀態1,則在t+1時刻分別有β1,α4,α5的概率向狀態0,2,3轉移,有1-β1-α4-α5概率保持狀態1;在t+2時刻,可從t+1時刻的狀態轉移至其他狀態。根據式(2)~(3),該模型的狀態轉移概率矩陣Pij如式(5)所示:
(5)
通過了解應急供應鏈中每個狀態的轉移概率,能夠動態識別、分析、應對風險。當供應鏈狀態逐漸向中斷狀態(狀態3)轉移時,能夠及時提醒供應鏈節點企業制定或修改應急措施,以減輕干擾風險;當供應鏈狀態逐漸向正常供應狀態(狀態0)轉移時,能夠體現出供應鏈的韌性特征,并驗證應急措施的有效性。
1.2 基于DTMC-MOP的應急供應鏈模型
突發災難事件的發生具有不確定性和突發性。當發生突發事件時,災區的應急物資需求量會急劇增加,在此之前相關部門應急物資的儲備量遠小于需求量,因此,需要將應急生產納入考慮范圍。應急供應鏈具有不確定性、強時效性和弱經濟性等特征,為制定高效的應急物資供應方案,本文提出DTMC-MOP模型,研究供應率、時間和成本3方面因素對應急供應鏈的影響。
1)模型假設
由于應急供應鏈涉及多個供應環節及多個節點企業,為簡化模型且不失一般性,本文提出以下3點假設:
假設1:應急供應鏈在0時刻處于狀態0,在t時刻進行第1步狀態轉移,在t+1時刻進行第2步狀態轉移,直到得到平穩概率分布,結束狀態轉移。
假設2:制造商沒有原材料和產品庫存,應急物資是收到供應商提供的原材料后進行生產制造,而后通過應急物流送往需求地。
假設3:模型僅考慮原材料、應急物資的生產時間和運輸時間,其他耗時忽略不計。
2)DTMC-MOP模型
I為供應鏈狀態i的集合,i∈I(i=0,1,2,3);T為時刻t的集合,t∈T(t=0,t+1,…);D為需求地d的集合,d∈D(d=1,2,…);S為供應商s的集合,s∈S(s=1,2,…);M為制造商m的集合,m∈M(m=1,2,…)。
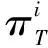
(6)
(7)
(8)
(9)
(10)
(11)
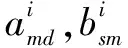
(12)
在DTMC-MOP模型中,式(6)描述最大供應物資滿足率目標,即最小化物資需求未滿足率;式(7)描述最短時間供應目標,即最小化原材料運輸時間、應急物資生產、運輸時間的總和;式(8)描述最低成本供應目標,即最小化供應商原材料成本和運輸成本以及制造商物資生產和運輸成本;約束(9)表示制造商M向需求地D供應物資的數量不超過需求地的物資需求數量;約束(10)是需求地D的物資需求滿足率公式,它等于物資的實際供應數量除以需求數量;約束(11)是離散時間馬爾科夫鏈中平穩概率分布公式;約束(12)表示決策變量為正整數。
2 改進NSGA-Ⅱ算法模型及評價
2.1 改進NSGA-Ⅱ算法模型
對于多目標規劃問題的求解,國內外學者進行大量研究,比較常見的求解方法包括將多目標轉化為單目標的精確算法[14-15]以及粒子群算法、模擬退火算法、遺傳算法等智能算法[16-18]。與前人研究相比,本文將采用收斂速度快、計算精確度高、計算復雜度低的NSGA-Ⅱ算法求解模型,但該算法在搜素性能、種群多樣性方面仍存在不足,為避免陷入局部最優,本文通過改進傳統NSGA-Ⅱ算法,進一步適應應急供應鏈風險快速、準確響應并決策的特性,提升算法的收斂速度和搜索能力。改進自適應NSGA-Ⅱ算法流程示意如圖2所示。
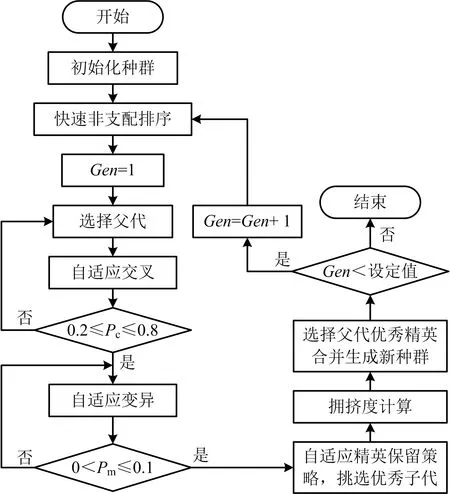
圖2 改進自適應NSGA-Ⅱ算法流程
1)初始化種群改進
在應急供應鏈實際應用中,初始數據較大且關系構造復雜,本文通過以下3個步驟對數據及編碼方式進行改進處理:
①采用實數編碼方式對初始自變量進行處理。
②運用反編譯將數據編碼范圍限定為0~1的隨機數乘以基數的形式,可以大幅提高算法的運行速度。
③對反編譯后的數據進行歸一化處理,構造種群規模N的初始種群E0。
2)自適應遺傳算子改進
①自適應多點交叉
在錦標賽選擇中得到N個新個體中隨機選擇2個個體進行多點交叉,算法中交叉點的位置和數量是隨機產生的。為避免陷入局部最優,本文采用自適應交叉法進行調節,從而大幅度提升算法的全局搜索能力。交叉概率Pc如式(13)所示:
(13)
式中:pfmax是該種群中適應度最大值;pf′為2個個體中適應度較大的值;pfmean為種群中平均適應度。
②自適應變異
隨機選擇交叉后的個體及基因位置以Pm的概率進行變異,如式(14)所示:
(14)
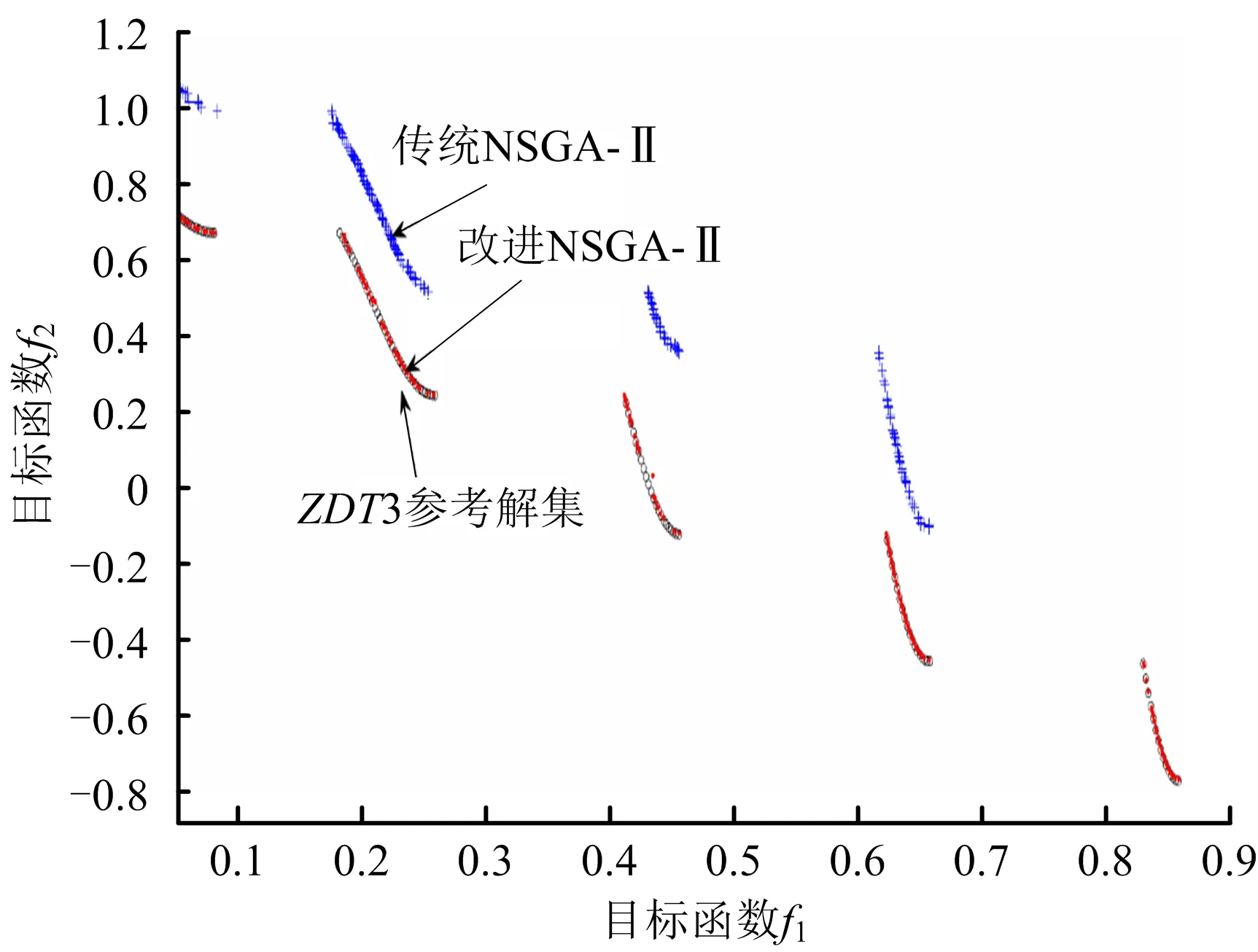
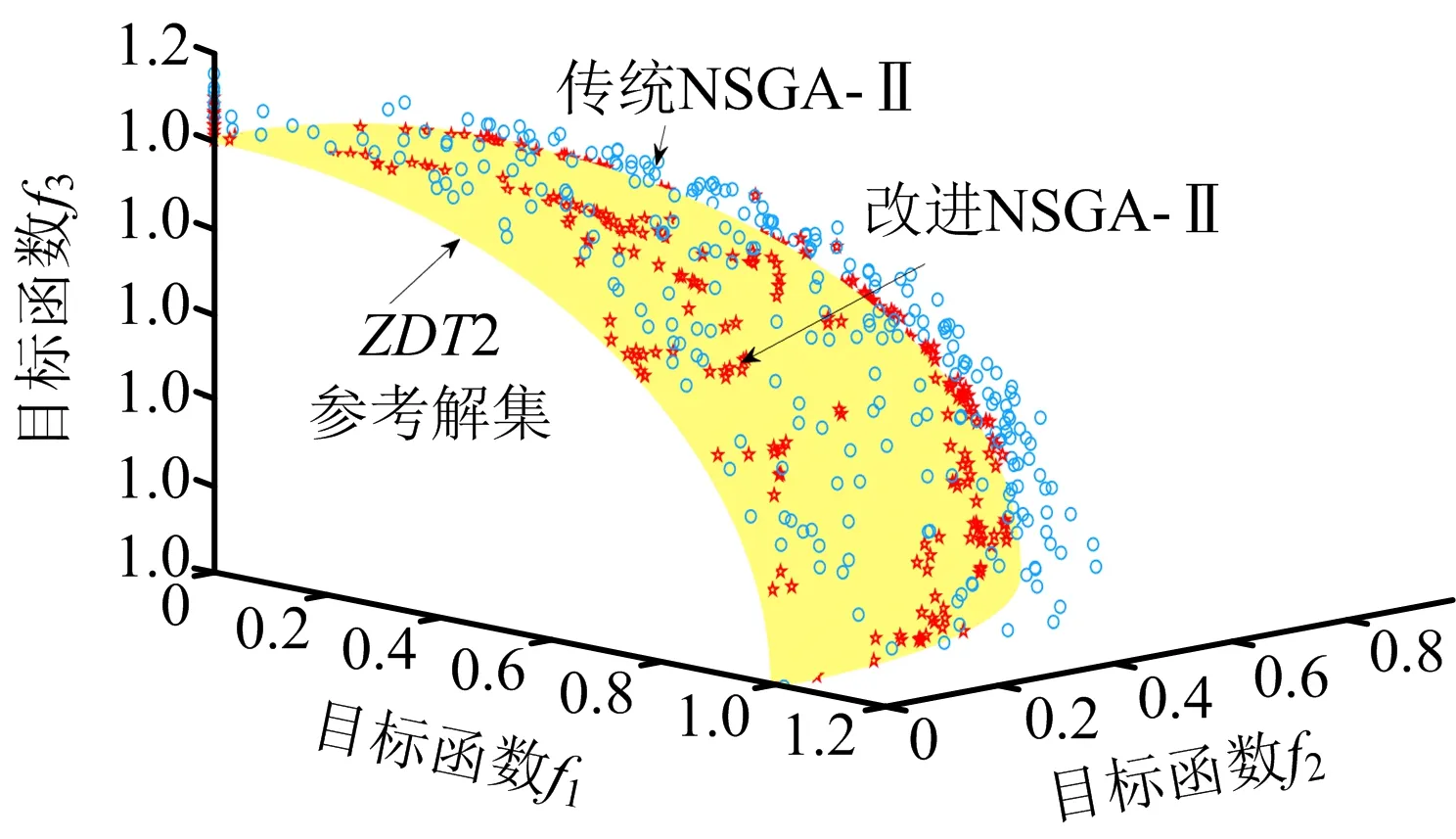
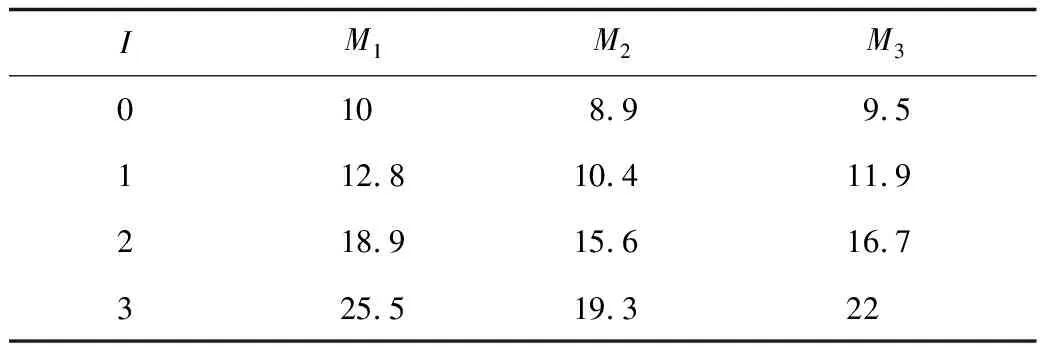
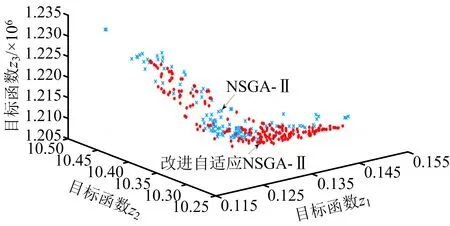
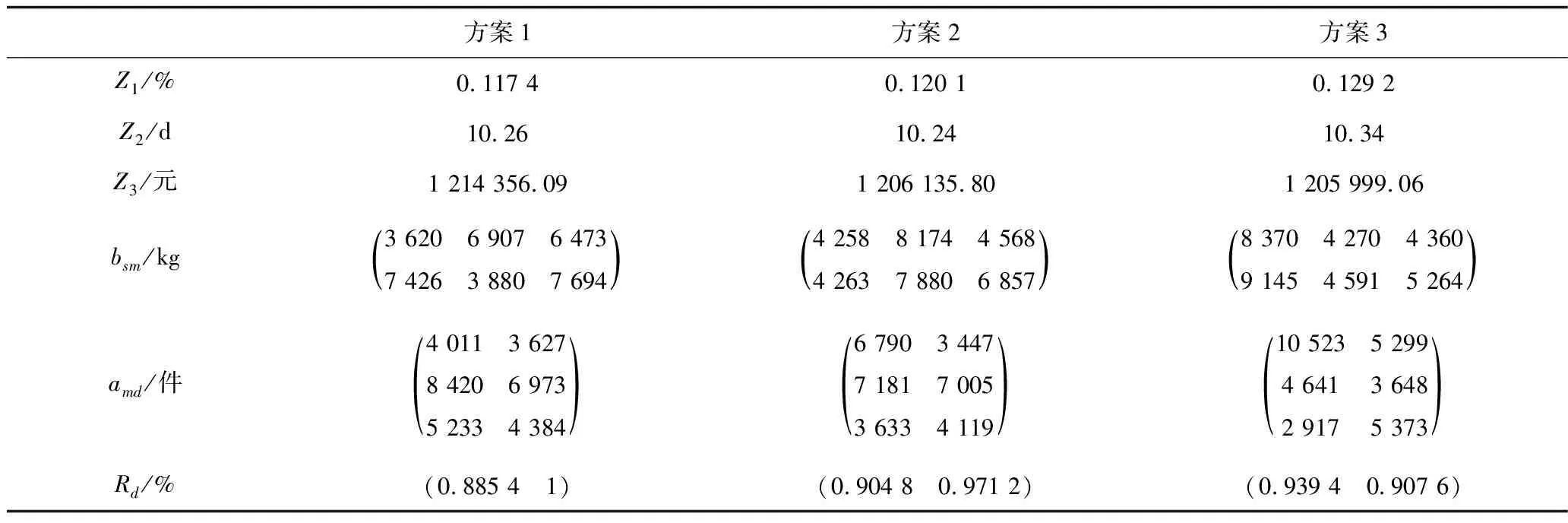
自適應變異算子0 3)自適應精英保留策略改進 將產生的子代種群Gn按式(15)隨機挑選出新子代精英種群NGn,同時為防止父代精英個體基因遺失,選擇父代種群En中Pareto等級低、擁擠度大的個體合并生成新種群Ln,直到Ln的規模達到N為止。該方法與傳統的父、子代種群合并生成新種群相比,前期精英規模較小,可以豐富種群的多樣性;后期隨精英規模增加,不斷提高種群的收斂性,可避免產生極端解,實現全局最優,如式(15)所示: (15) 式中:an為第n代精英保留規模的影響因子。 應用多目標化算法解決實際問題時,主要從分布性及收斂性2方面進行分析。因此,本文將從基于歐氏距離的收斂性[19]和分布性指標[20]進行評估。 1)世代距離的收斂性指標 收斂指標ca可以評估算法理想的Pareto最優前沿程度,定義如式(16)所示: (16) 式中:Nd為算法求出的非支配向量個數;di為算法已知個體邊界與真正Pareto的歐幾里得距離。 2)空間評價的分布性指標 指標sa用于評價多目標優化算法所求的解集的分布性,如式(17)所示: (17) 本文通過標準測試函數ZDT3和DTLZ2對該模型進行測試與評估,并與傳統NSGA-Ⅱ算法對比,2種測試函數最優前沿對比如圖3~4所示。 圖3 ZDT3測試函數最優前沿比較 由圖3可知,改進個體與參考解集基本重合,而傳統算法解集個體則與參考值存在偏差。由圖4可知,改進算法求得的個體緊密附著于Pareto前沿,而未改進算法求解的個體大多漂浮于Pareto前沿,甚至有少數個體脫離。由此,改進的NSGA-Ⅱ算法更接近最優Pareto前沿,算法精度相對更高。 圖4 DTLZ2測試函數最優前沿比較 假設我國某地區發生突發災難事件,應急管理部門需要制定應急預案,并根據實際情況及時對應急方案進行調整。根據該地區目前災情和以往發生災害情況,該地區有2個需求地D1,D2,需要應急生產和運輸某應急物資共35 000件;由2個供應商S1,S2提供原材料,1 kg原材料可生產1件應急物資,其中S1最多可供應19 000 kg,S2最多可供應17 000 kg;3個制造商M1,M2,M3負責應急物資的生產和運輸。本文運用DTMC-MOP模型模擬應急生產與調度情況,制定最佳應急方案。該模型具體參數設置如下: 應急供應鏈初始狀態概率分布P0及狀態轉移概率矩陣Pij如式(18)所示: (18) 本文運用MATLAB R2020b軟件編程求解模型。首先依據式(4)、初始概率分布P0和狀態轉移概率矩陣Pij經過200次迭代實現應急供應鏈狀態的動態轉移,求得唯一平穩概率分布π=(0.461 0 0.294 8 0.169 8 0.074 4),將表1~5的參數依據平穩概率分布進行加權處理,并輸入如下參數:Cs1=6.3,Cs2=6.5,元;Cm1=18,Cm2=19.5,Cm3=19,元;k1=89,k2=92,k3=90,%;Q1=20 000,Q2=15 000,件。其次,對于改進的NSGA-Ⅱ算法基礎參數設置如下:種群規模N=200,自適應交叉概率Pc在0.2~0.8之間,變異概率Pm在0~0.1之間,最大迭代次數MG=200,運行2種算法程序得到Pareto最優前沿,如圖5所示。 表參數設置 表參數設置 目標函數Z1供應物資需求未滿足率大小、Z2供應時間長短以及Z3供應成本高低3者之間的關系。由圖5可知,最優解在三維空間中形成1個分布均勻的曲面,能夠較好地收斂于Pareto最優前沿,改進自適應NSGA-Ⅱ算法曲線分布在傳統算法曲線下方,獲得更貼近理想值的Pareto前沿,目標結果更優。 表參數設置 表參數設置 表5 ti參數設置 圖5 Pareto最優前沿 從改進自適應NSGA-Ⅱ算法的Pareto最優前沿中分別選取單個目標函數值最小的3組具有代表性的解,見表6。根據決策者的偏好差異可以選擇不同的解決方案,若決策者傾向于物資未滿足率最低,最佳方案是方案1;若決策者追求物資供應時間最短,應該選擇方案2;若決策者希望實現最低的物資供應成本,方案3是最好的選擇;若決策者想綜合考慮3方面的因素,可以在其他Pareto最優前沿中選擇相適應的應急方案。 表6 Pareto典型解 1)提出DTMC-MOP模型,制定有效的應急物資生產與調度方案。基于DTMC模型中的狀態轉移概率矩陣刻畫應急供應鏈的動態性特征,可用于識別、分析、應對應急供應鏈風險。在此基礎上結合MOP模型,構建供應物資滿足率最大、供應時間最短、供應成本最低的DTMC-MOP模型,運用該模型可以很好地解決因風險擾動引起的生產、運輸能力變化,得到3個目標的總體最優策略。 2)采用改進自適應的NSGA-Ⅱ算法求解模型,優化算法的收斂性和分布性,得到精度更高、更加貼近理想Pareto最優前沿的結果。通過改進初始化種群、自適應交叉和變異算子、自適應精英保留策略,提高算法的全局、局部搜索能力,決策者可以依據應急管理核心目標或是不同的偏好選擇相適應的應急方案。2.2 模型評價指標
2.3 模型測試結果與分析
3 算例分析
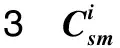
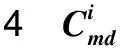
4 結論

