無煙煤對超臨界態CH4-CO2氣體吸附特性研究*

張明杰，周 巍，楊 娟，梁錫明，李 哲

(1.河南省瓦斯地質與瓦斯治理重點實驗室-省部共建國家重點實驗室培育基地，河南 焦作 454003；2.河南理工大學 安全科學與工程學院，河南 焦作 454003；3.中原經濟區煤層(頁巖)氣河南省協同創新中心，河南 焦作454003)

0 引言

我國1 200 m的深部煤層煤層氣儲量可達1.677×1013m3[1-2]。相比開采4 000 m以下的頁巖氣而言，具有更廣闊的開發空間。目前，提高煤層氣采收率的有效措施有水力壓裂技術、多分支水平井和CO2-ECBM等，其中CO2-ECBM技術不但可以將大量的CO2封存于地下，同時可以提高煤層氣采收率，增加礦井的經濟效益[3]。

為改善注氣驅替技術，大量學者進行了純氣體注氣實驗，研究變量主要有注氣壓力、方式以及類型[4-6],也有學者開展了二元及多元氣體競爭吸附實驗從而得到多元氣體吸附等溫線[7-8]。但是眾多學者所模擬的條件未達到超臨界條件，不能代表深部煤層的吸附規律。目前所開采的煤層中深部一般為高階煤層[9]，考慮地溫梯度和地壓梯度[10]，煤層瓦斯壓力及溫度均超過CH4及CO2的臨界值，二者進入非固液氣的第四態—超臨界態，其密度及黏度接近液體，擴散性質近似氣體[11]，不能將其視為常規氣體或液體進行討論，傳統的吸附模型理論已不再適合該狀態下的吸附量計算[12-13]。

為此，本文運用重量法開展超臨界條件下無煙煤對純CH4、純CO2及3種不同組分的CH4-CO2二元混合氣體等溫吸附實驗并對其絕對吸附量以及吸附分子層數進行分析，希望可以為CO2的地質封存以及煤層氣的儲量評估提供一定的幫助。

1 實驗裝置及煤樣分析

選用焦作九里山無煙煤，制成粒徑0.18～0.25 mm顆粒煤樣，進行工業分析，并采用壓汞法和液氮吸附法測定煤樣比表面積，見表1。

本文采用磁懸浮天平進行吸附實驗，如圖1所示。該儀器吸附環境與天平處在不同環境，在不接觸的情況下對重量進行測定，不會受到吸附質的影響。測量精度可達10-6g，吸附室的最大壓力可達50 MPa，溫度最大可達200 ℃。

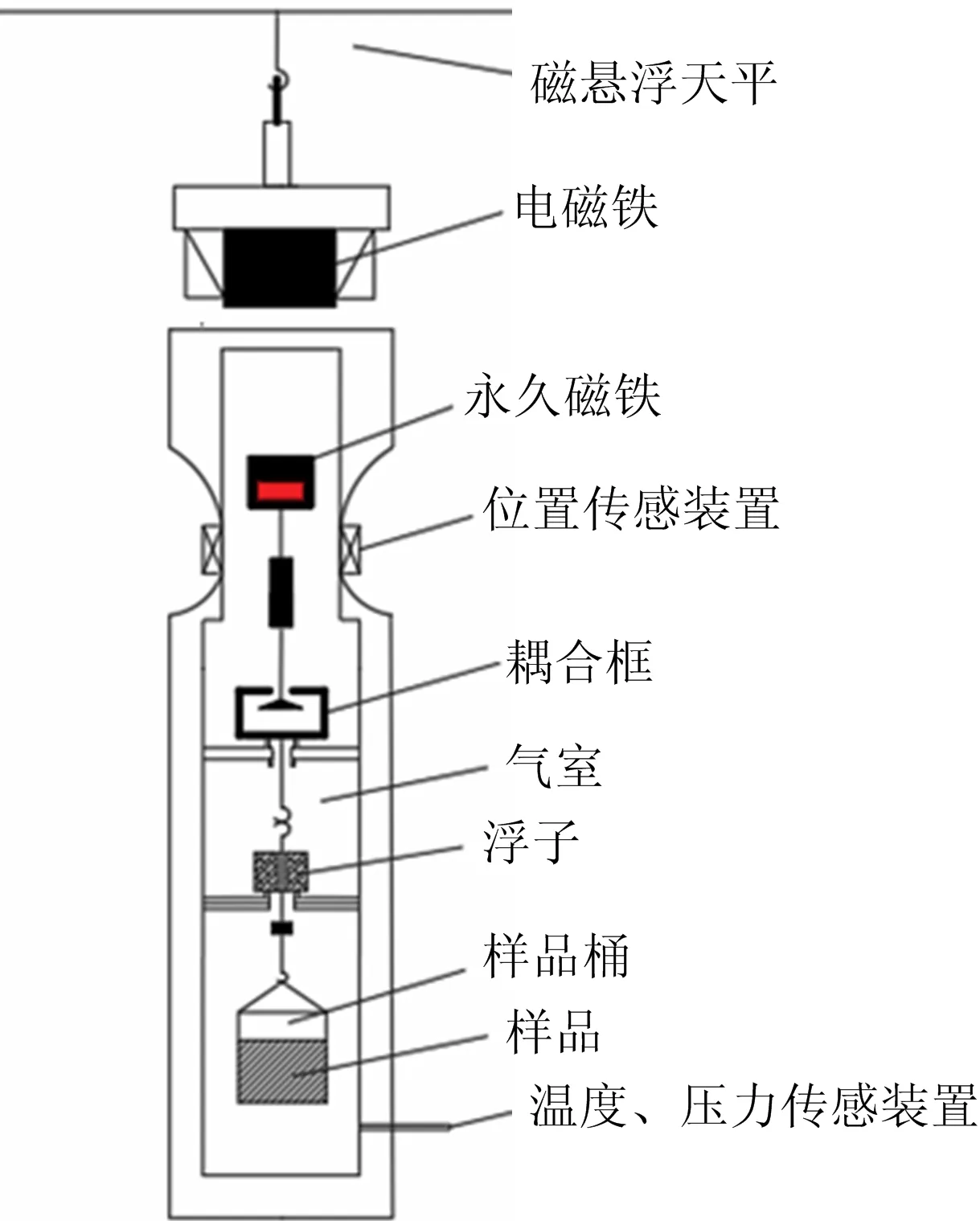
圖1 磁懸浮天平結構

1.1 實驗原理

本文實驗儀器基于阿基米德浮力原理測定得到數據和圖像。電磁鐵提供的拉力Fex、整體重力Fm以及所受浮力f三力平衡，進行吸附量計算。本文假設煤顆粒受氣壓影響不發生收縮變形。此時有式(1)～(5)：

Fm=(ms+msc+ma)g

(1)

f=(Vs+Vsc)gρ

(2)

Fex=(ms+msc+ma)g-(Vs+Vsc)gρ

(3)

Δm=ms+msc+ma-(Vs+Vsc)ρ

(4)

ma=(Vs+Vsc)ρ+Δm-ms-msc

(5)

式中：Fex為電磁鐵提供拉力，N；Δm為天平示數，g；ms為煤樣質量，g；msc為樣品桶質量，g；ma為吸附氣體質量，g；Vs為煤樣體積，cm3；Vsc為樣品桶體積，cm3；ρ為游離相密度，g/cm3；g為重力加速度，取值9.8 m/s2。

1.2 實驗前需進行步驟

1)空白測試：測定樣品桶質量和體積。設置40 ℃，5個壓力點向吸附室內通入3 MPa氦氣，結合式(4)進行線性擬合，斜率為樣品桶體積。

2)煤樣預處理：對于放入煤樣的系統設定120 ℃，真空處理300 min，去除煤樣雜質。

3)浮力測試：測定預處理后的煤樣質量和體積。設定40 ℃，5個壓力點通入3 MPa氦氣，所得數據結合式(4)擬合得到煤樣的體積及重量。

4)等溫吸附實驗：設定溫度40 ℃，壓力為0～15 MPa，每個壓力點平衡12 h以上，實驗結束后，收集吸附平衡后吸附室內游離氣體，進行游離氣樣的比例分析。

2 單元氣體吸附實驗

為對比分析二元氣體吸附特征，首先采用相同煤樣進行CH4，CO2單元氣體等溫吸附實驗。完成前文中預處理各項步驟后對吸附室抽真空，使用純度為99.999%的CH4和CO2開始吸附實驗。實驗曲線如圖2所示。

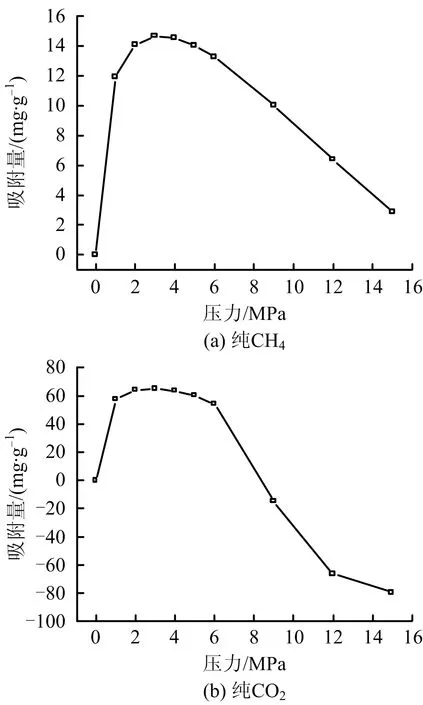
圖2 單元氣體等溫吸附實驗曲線

CH4，CO2的實驗曲線均在3 MPa左右出現峰值，之后隨著壓力增大吸附量逐漸減小。原因是原本可忽略不計的吸附相所產生的浮力對吸附量的計算產生了影響[14]。由實驗條件可知，此時2實驗氣體發生了超臨界吸附，低壓時為初始吸附階段，吸附環境中游離氣對吸附相產生的浮力較小，可忽略；隨著氣壓增大，該浮力影響已無法忽略。目前儀器無法直接測定吸附相體積大小[15]，則需對吸附相體積進行計算及校正實驗曲線。

因考慮吸附相體積，則式(1)～(5)均需加入吸附相體積Va，而Va無法測定，在此引入Gibbs吸附量me[16]，與真實吸附量的關系如式(6)進一步轉化為式(7)：

me=ma-ρVa

(6)

(7)

式中：me為Gibbs吸附量，g；ma為吸附氣體質量，g；ρ為游離相密度，g/cm3；ρa吸附氣體密度，g/cm3。

本文利用截距法[14]進行矯正，對Gibbs吸附曲線與游離相密度關系圖中的下降段進行擬合得出吸附相密度(所擬合的直線與x軸的交點)，如圖3所示。將擬合所得吸附相密度、實驗所得Gibbs吸附量和游離相密度帶入式(7)，得到絕對吸附量曲線如圖3所示。結果顯示相同狀態下CO2的真實吸附量約為CH4真實吸附量的5倍，隨著壓力的增大，真實吸附量逐漸達到吸附飽和。

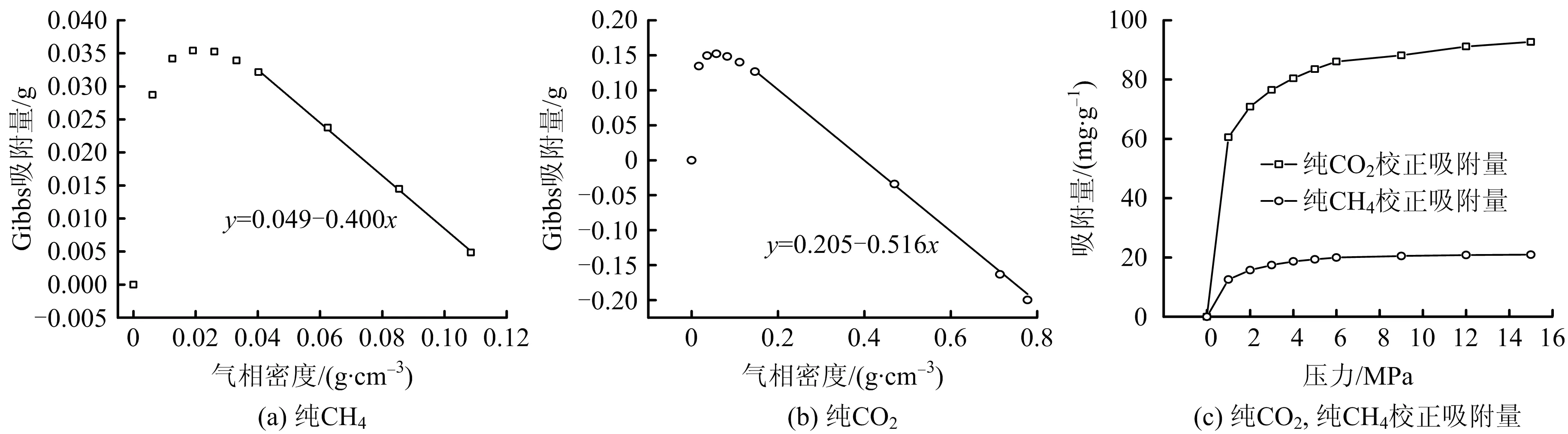
圖3 單元氣體吸附相密度及校正曲線

3 二元混合氣體吸附實驗

3.1 二元混合氣體吸附測定

為探究CH4及CO2的競爭吸附特征，本文實驗采用3種CH4∶CO2的摩爾組分比氣樣，分別為：76.37%∶23.63%，53.10%∶46.90%以及21.74%∶78.26%；分別命名為高濃度CH4、中濃度CH4以及低濃度CH4。實驗溫度設置為313.15 K，壓力為0～15 MPa。為保證實驗中每一壓力點進氣比例穩定，在每一壓力點吸附平衡后對吸附池及煤樣進行120 ℃維持真空狀態4 h的除雜處理，并取部分氣樣進行氣相色譜分析平衡后游離氣體各組分占比。

運用相同方法校正混合氣體Gibbs吸附曲線，如圖4所示。3種不同配比混合氣體的Gibbs吸附曲線隨著CH4濃度的降低，逐漸向CO2吸附曲線靠近；其擬合所得吸附相密度也隨CH4濃度降低而逐漸增大；校正所得真實吸附量隨CH4濃度的降低呈梯度式增大的趨勢，并且大于CH4小于CO2，混合氣體中CO2濃度越高其真實吸附量越接近純CO2，吸附趨勢也與其接近。對于游離氣體氣相色譜分析，得到各組分游離氣體積比，如圖5所示。

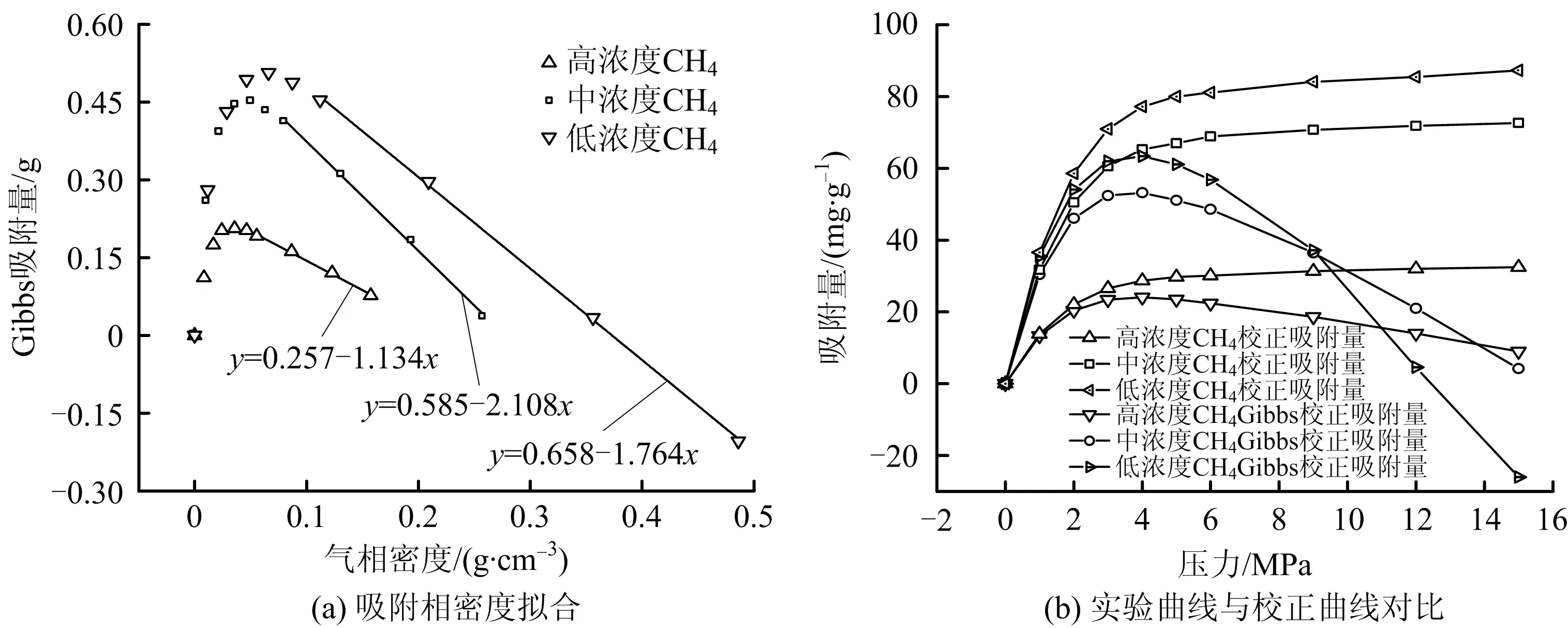
圖4 不同比例混合氣體吸附相密度擬合線、實驗吸附曲線及校正吸附曲線

由圖5可知高濃度CH4混合氣體在各壓力點達到吸附平衡以后，游離氣體中 CH4占比小于初始占比，CO2占比始終高于初始占比；中、低濃度CH4混合氣體與其相反，表明高濃度CH4混合氣體，煤樣吸附CO2量小于CH4，中濃度CH4和低濃度CH4混合氣體，吸附CO2量大于CH4。隨著壓力的增大，吸附逐漸趨于飽和，同時因吸附池體積不變，通入氣體總量逐漸增加，吸附氣體量對游離氣體積比影響逐漸減小，導致高壓下氣體比例逐漸趨于初始比例。

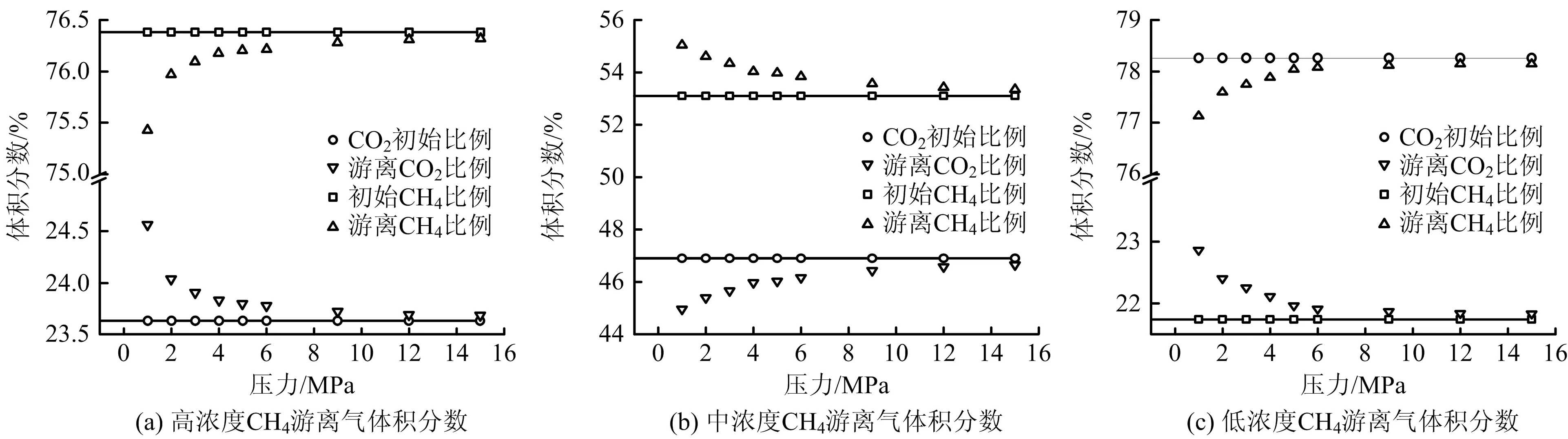
圖5 混合氣體吸附平衡后游離氣體組分變化

3.2 混合氣體吸附相組分分析

實驗無法直接獲取混合氣體中各組分吸附量，需進行計算。首先將初始進氣的體積比轉換為質量比。設通入混合氣體中CH4質量為x進；CO2質量為y進；吸附相中吸附CH4質量為A；吸附CO2質量為B；Q進為CH4進氣所占質量比；P進為CO2進氣所占質量比；P游為游離CO2所占質量比；Q游為游離氣體CH4所占質量比；總吸附量為q，mg/g，游離氣比例及吸附環境體積為V，cm3，應用式(8)計算二元組分吸附量。

(8)

計算得到吸附相各組分吸附量，如圖6所示，吸附相中各組分體積比見表2。

圖6顯示在吸附平衡狀態下，3種混合氣體中CH4組分吸附量均小于純CH4吸附量；隨著進氣CO2占比增加，煤樣吸附CH4量降低，混合氣體總吸附量隨著CO2比例增加逐漸向純CO2靠近。表2顯示吸附相中各組分體積比不等于原始進氣比。高濃度CH4氣樣吸附相中CO2組分所占體積比小于初始占比，隨著氣壓升高吸附相中CO2組分占比緩慢升高；中濃度CH4氣樣吸附相中CO2吸附量占比明顯大于原始氣樣占比，隨氣壓升高吸附相中CO2組分占比緩慢升高；低濃度CH4氣樣吸附相中CO2吸附量占比也明顯大于原始氣樣占比，隨著氣壓升高吸附相中CO2組分占比緩慢升高。

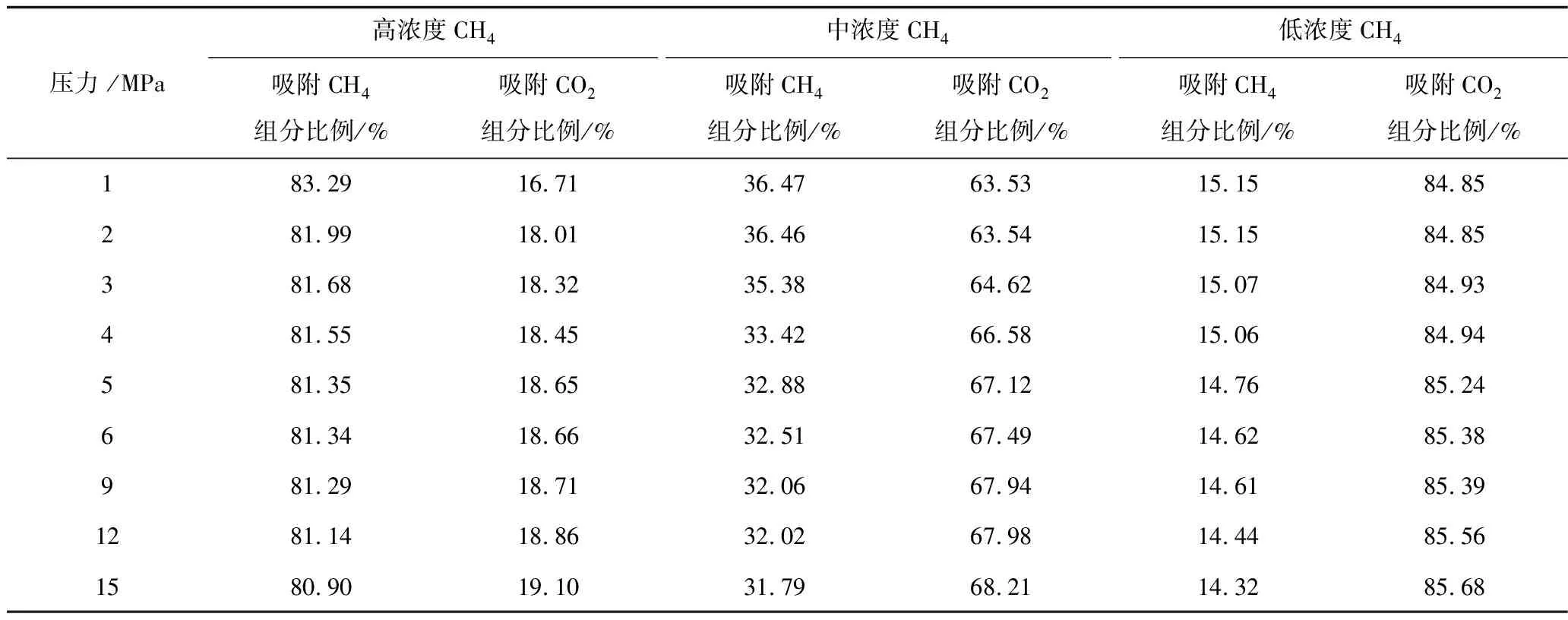
表2 吸附相各組分吸附比例

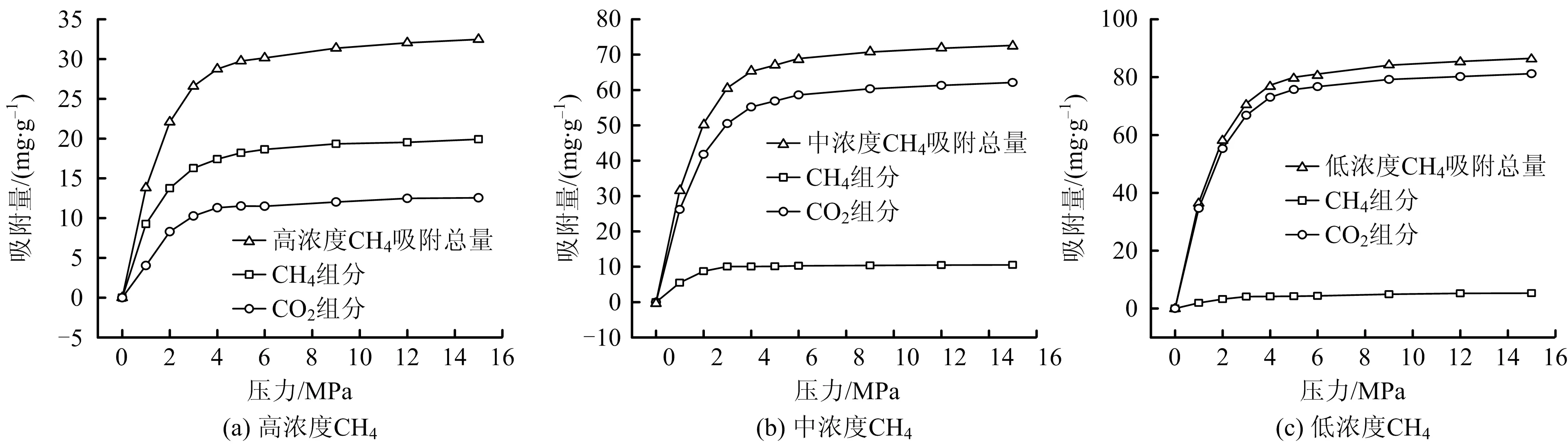
圖6 混合氣體總吸附量及各組分吸附量

4 二元混合氣體吸附特征

4.1 CH4與CO2單組分吸附層分析

吸附分子層數可以反映各氣體的吸附特征。本文以Langmuir理論為基礎探究單元氣體吸附方式，以二者吸附量計算煤比表面積。假設吸附在煤表面的氣體分子成隊列式緊湊分布且平鋪于煤的表面。在計算時不應只考慮計算氣體分子，分子間的空隙也應當計算在內。

CH4與CO2分子直徑約為0.48 nm，因此，本文對煤表面積的計算采用CH4氣體吸附量計算煤樣比表面積。利用實驗測定低壓段CH4吸附數據與Langmuir模型進行擬合，得到單層極限吸附量a=16.68 mg/g。假設CH4分子在煤顆粒表面被均勻吸附、規則排列，則CH4分子之間會構成正四邊形或者正三角形(蜂巢型)2種規則的排列方式，本文選定正四邊形為煤顆粒表面吸附甲烷分子的排列方式，如圖7所示，求得煤比表面積為144.62 m2/g。CH4分子在煤表面覆蓋時不會如此規整緊密排列，因此，在計算吸附層數時以80%的覆蓋率計算2種氣體在煤樣中的吸附層數，計算結果見表3。

圖7 煤表面吸附氣體分子排列示意

由表3可知1～3 MPa，CH4以單層吸附為主，會出現2層吸附趨勢，9 MPa以后層數基本穩定；CO2在1～3 MPa壓力下以2層吸附為主，并局部出現3層吸附。隨著壓力增大普遍為3層吸附，局部出現4層吸附。

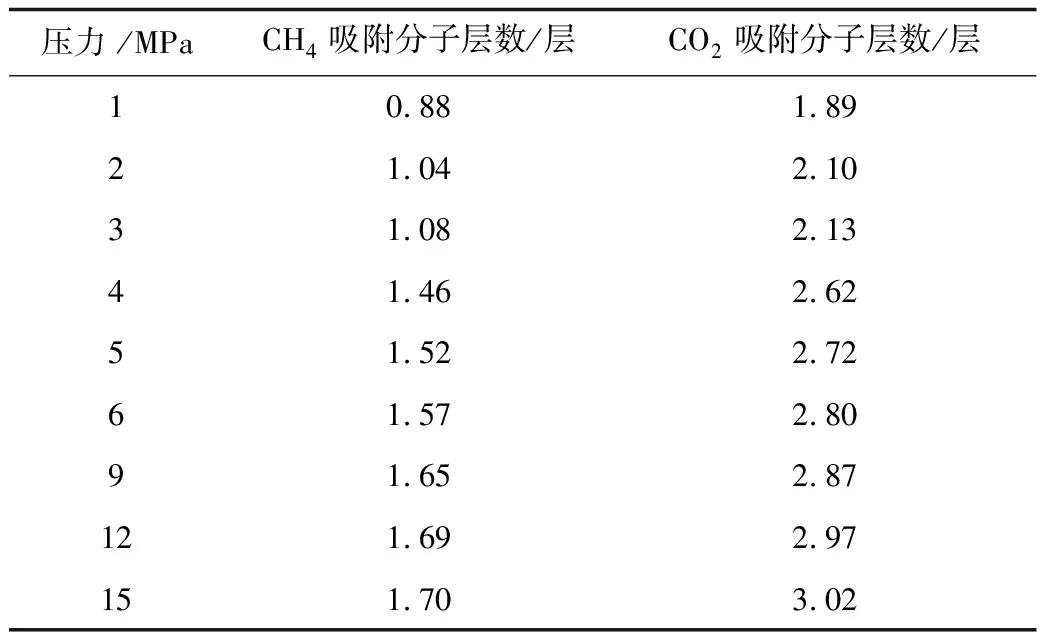
表3 煤顆粒吸附單元氣體分子層數

4.2 二元吸附特征分析

受壓后煤顆粒表面原子化學鍵斷裂，受到向煤體內部的引力，這些原子因此獲得能量，該能量為表面自由能[17-18]。根據能量最低原理，煤表面原子會朝著能量最低方向運動，但這些原子并不會真正發生向內位移，而是通過吸附周圍分子來降低自身能量。煤顆粒吸附不同氣體分子時表現出的表面自由能不同，該差異決定了不同吸附質能力的差異。由于自由能分布不同，導致吸附集中區發生，本文視吸附區域為均勻吸附[19]。

煤顆粒表面吸附氣體分子后，表面濃度會大于煤顆粒內部氣體濃度，內外濃度之差稱為表面超量Г，mol/m2，如式(9)所示：

(9)

式中：V為吸附量，mL；Vm為標況下氣體摩爾體積，22.4 L/mol；S為煤比表面積，m2/g。

累計表面自由能降低值見式(10)[20]：

(10)

對式(10)進一步改寫為式(11)：

(11)

式中：Δγ為累計自由能降低值，J/m2；T為溫度，K；R為氣體常數，8.31 J/(mol·K)；P為壓力，MPa；K為參數取1 MPa-1；Vc為2～15 MPa校正后吸附量，g。將Langmuir吸附量Vp及吸附常數a，b代入積分范圍為0～1的積分項中，得式(12)：

Δγ=RTΓ(aln(1+Kb)+Vcln(KP))

(12)

根據上述公式計算結果，單元氣體表面自由能變化如圖8所示。

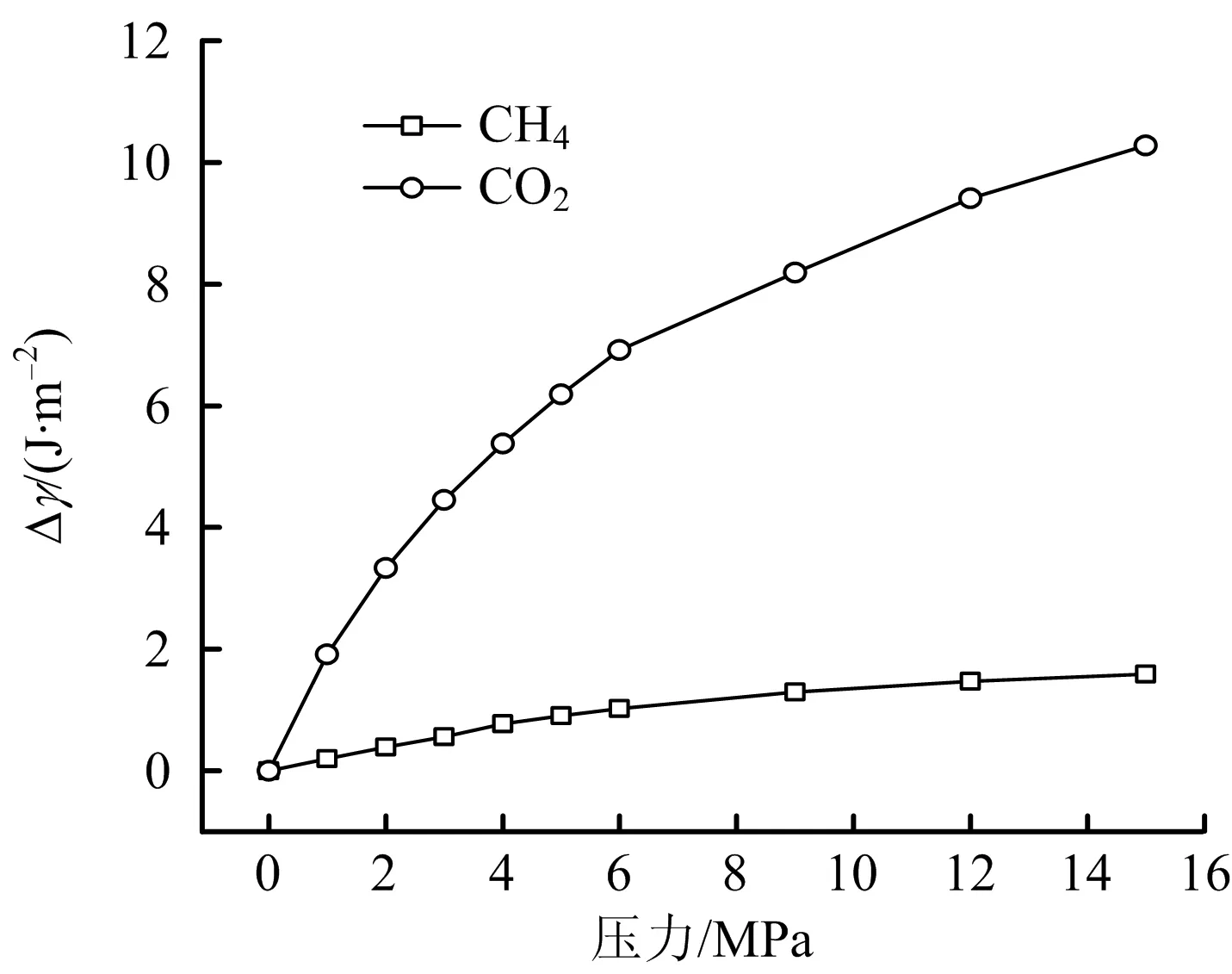
圖8 單元氣體表面自由能變化

圖8顯示，隨著壓力增高，表面自由能降低值增大，表明自由能越高吸附量越大。在吸附過程中，隨著壓力增大，吸附質分子首先吸附于高能量吸附位，隨著壓力增大開始逐步吸附于低能量吸附位，表面自由能下降速率逐漸變緩。相同壓力下，煤顆粒吸附CO2表面自由能降低值大于CH4；CO2進入超臨界態后，表面自由能絕對值與增大速率大于CH4，說明超臨界態CO2更易被煤樣吸附，這也是能夠發生多層吸附的原因，也表明煤層對于CO2有更大的儲存能力。

5 結論

1)單元氣體過剩吸附曲線在3 MPa附近出現峰值，二元氣體吸附曲線在4 MPa附近出現峰值，之后過剩吸附量逐漸減小，原因是游離氣體對吸附相產生的浮力所致。

2)隨壓力增大CH4與CO2絕對吸附量不斷增大。接近臨界壓力4.59 MPa時，絕對吸附量增加變緩并趨于穩定，CH4以單分子層吸附為主，局部為2層吸附。1～3 MPa低壓條件下CO2即以2層吸附為主，15 MPa壓力時局部吸附層可達4層，超臨界態下的CO2較常態下，更易于地質封存及驅替CH4。

3)進入超臨界態后，CH4及CO2氣體分子表面自由能降低速率明顯加快，釋放能量增多，煤顆粒吸附CO2表面自由能下降值明顯大于CH4。