相位鎖定指示值與GNSS觀測值質量分析
彭 會,戴吾蛟,余文坤,潘 林,鄭 彬
相位鎖定指示值與GNSS觀測值質量分析
彭 會1,戴吾蛟1,余文坤1,潘 林1,鄭 彬2
(1. 中南大學 地球科學與信息物理學院,長沙 410083;2.湖南北云科技有限公司,長沙 410083)
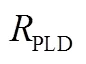
相位鎖定指示值;全球衛星導航系統;質量分析;隨機模型
0 引言
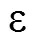
1 相位鎖定指示值
圖1 接收機跟蹤環路

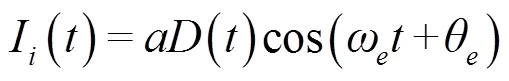


圖2 信號I和Q的表達
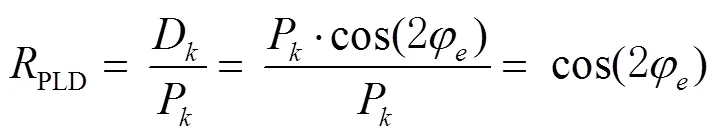
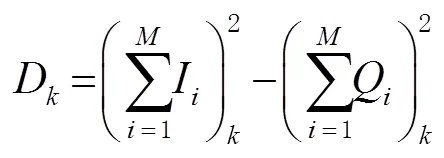
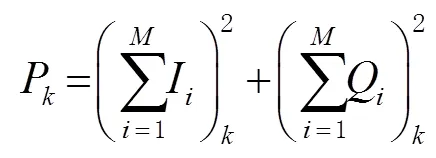

2 RPLD與GNSS觀測值質量分析
2.1 觀測環境與數據采集

圖3 觀測環境


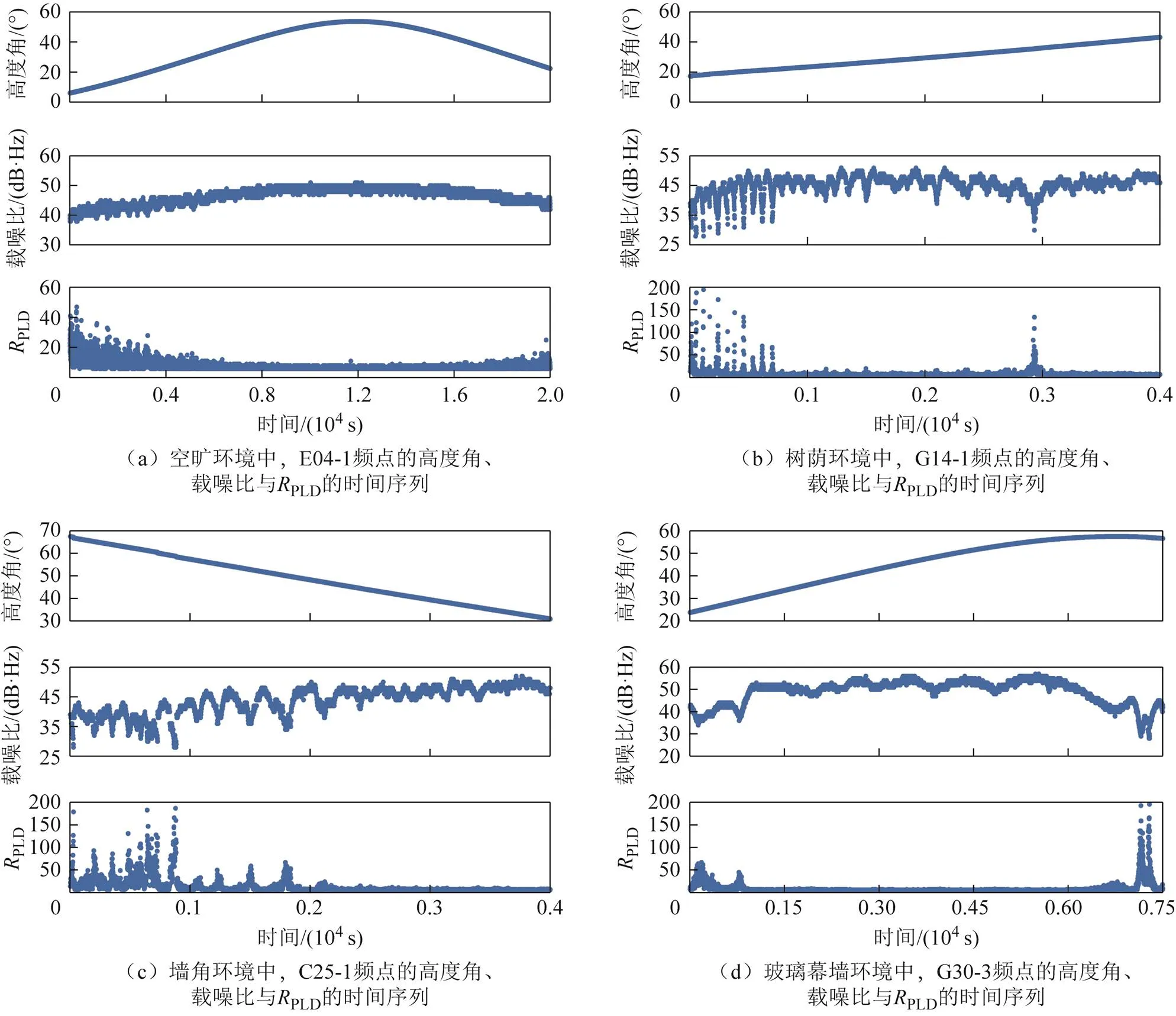
圖4 不同環境中高度角、載噪比與的時間序列


圖5 不同環境、不同系統各顆衛星不同頻率的載噪比與相關系數

式中:Slp為周跳發生概率;Slp為周跳歷元數;obs為數據總歷元數。
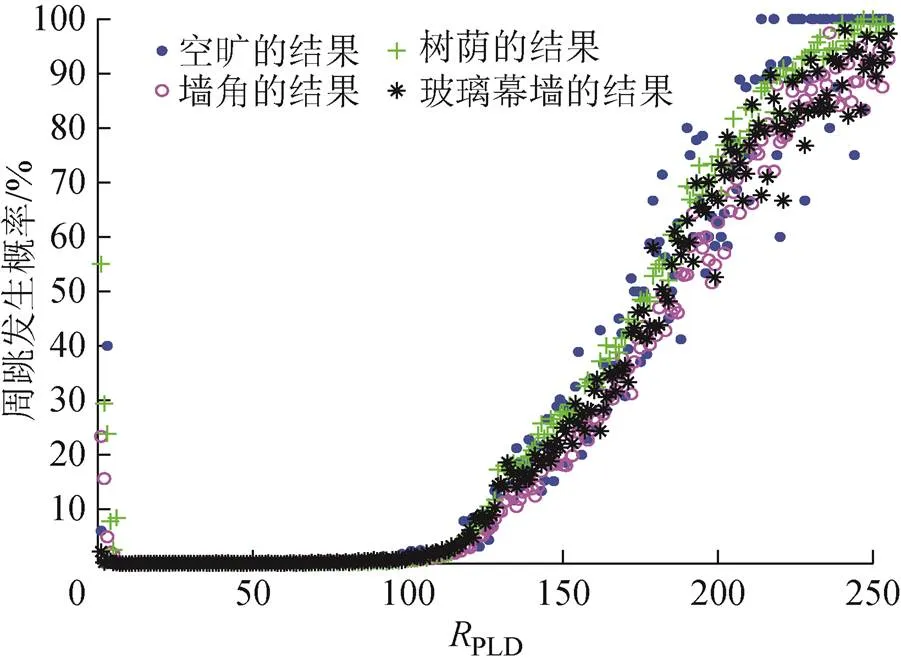
圖6 與周跳發生概率關系

表1 不同的對應的周跳發生概率
2.3.2 載噪比與周跳相關性分析
圖7展示了空曠、樹蔭、墻角和玻璃幕墻環境中,不同載噪比對應的周跳發生概率。由圖7可知,不同環境中,相同載噪比對應的周跳發生概率不完全一致。在4個環境中,當載噪比從1 dB·Hz增加至32 dB·Hz時,周跳發生概率未隨載噪比增加而下降,而是頻繁地上下波動。當載噪比大于32 dB·Hz后,周跳發生概率趨于穩定,其值趨近于零。但是,在樹蔭、墻角和玻璃幕墻環境中,隨著載噪比增大至55 dB·Hz左右時,周跳發生概率突然增大,而且一直保持著較高頻率,這可能是由于多徑信號或衍射信號疊加導致載噪比大于正常值。由此可見,復雜環境中載噪比大小無法完全反映周跳發生概率。
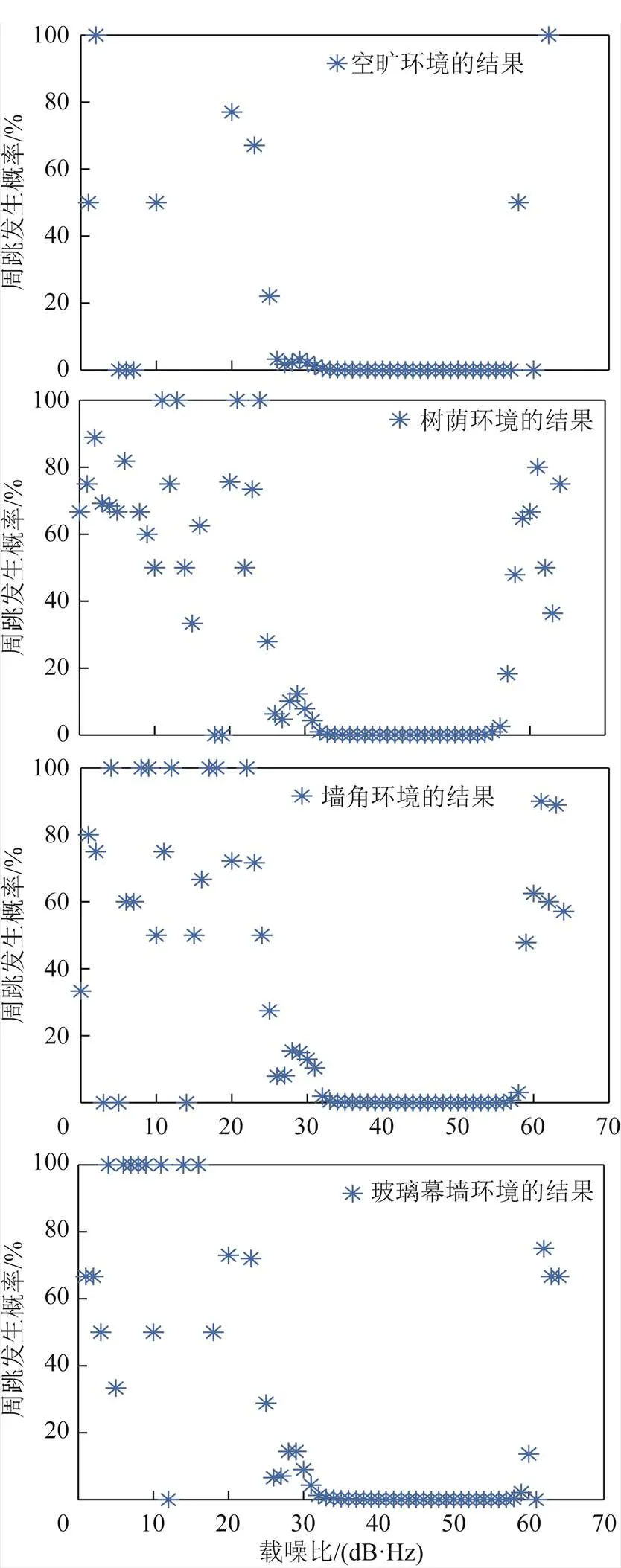
圖7 不同載噪比對應的周跳發生概率
2.3.3 高度角與周跳相關性分析
圖8展示了空曠、樹蔭、墻角和玻璃幕墻4個環境中,不同高度角對應的周跳發生概率。由圖8可知,在空曠環境中,隨著高度角升高,周跳發生概率隨之下降并逐漸趨于穩定。在樹蔭、墻角和玻璃幕墻環境中,隨著高度角升高,周跳發生概率隨之降低,但高度角上升過程中,周跳發生概率頻繁波動。在樹蔭和墻角環境中,當高度角大于75°后,周跳發生概率顯著增大。由上述分析可知,高度角與周跳發生概率的相關性也明顯受到環境因素影響。
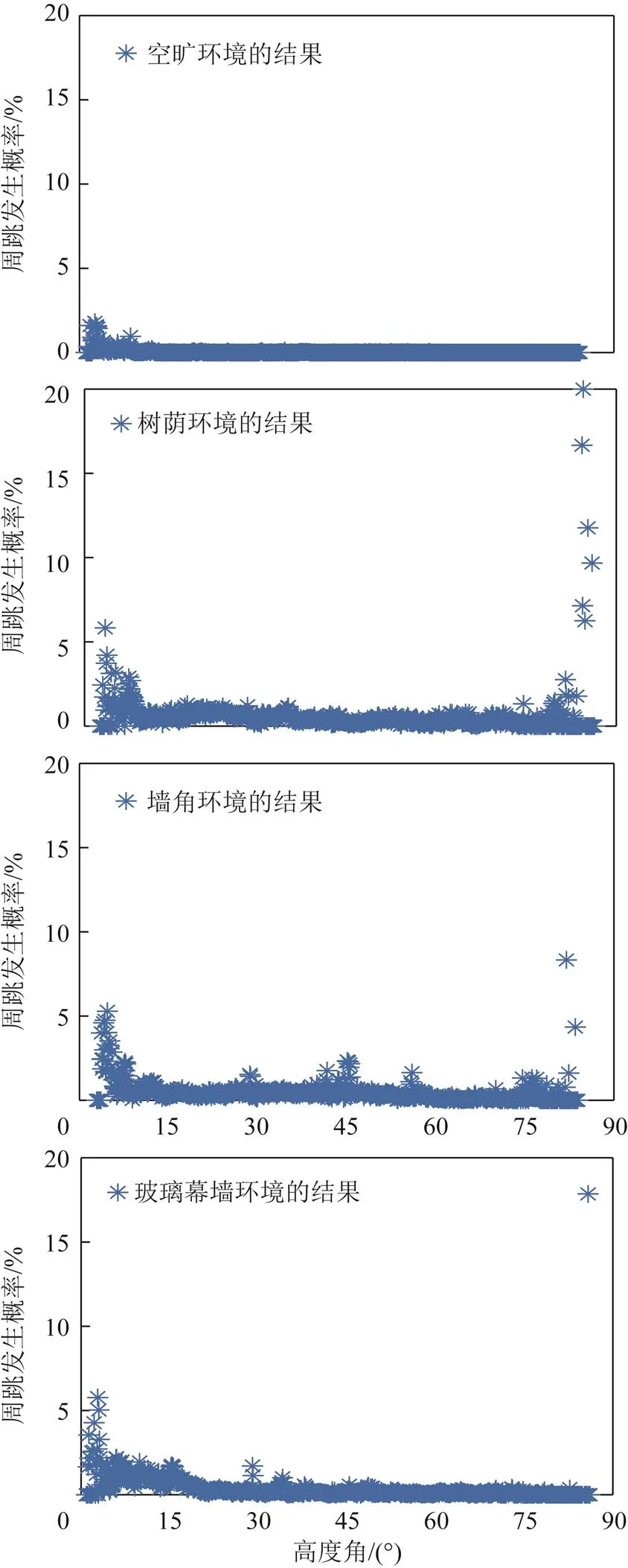
圖8 不同高度角對應的周跳發生概率
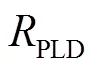
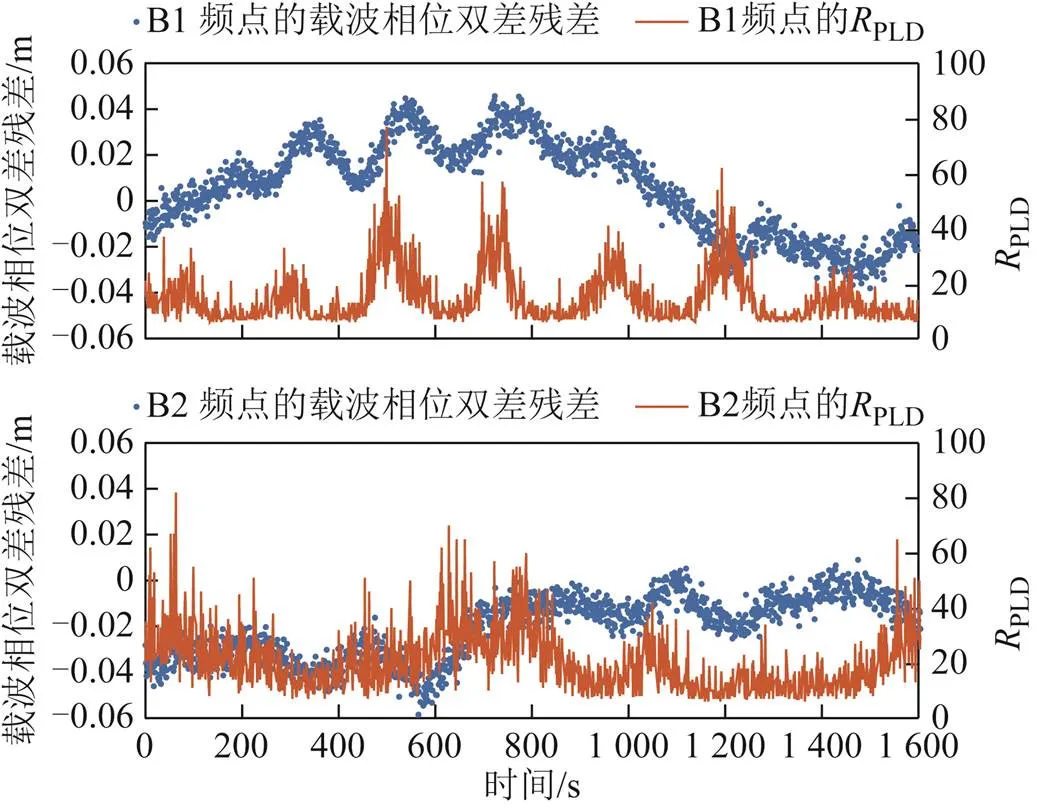
圖9 C16的載波相位雙差殘差和時間序列圖
2.4.2 載噪比與載波相位雙差殘差相關性分析
圖10為C16的載波相位雙差殘差和載噪比時間序列圖,從圖9可以看出,B1和B2頻點的載噪比和載波相位雙差殘差的總體變化趨勢和周期性變化部分都高度一致,但載噪比的周期性變化部分和載波相位雙差殘差周期性變化部分之間存在一定的時延。這是因為載噪比估計的平滑周期一般較長,可能用1 s的數據來平滑。
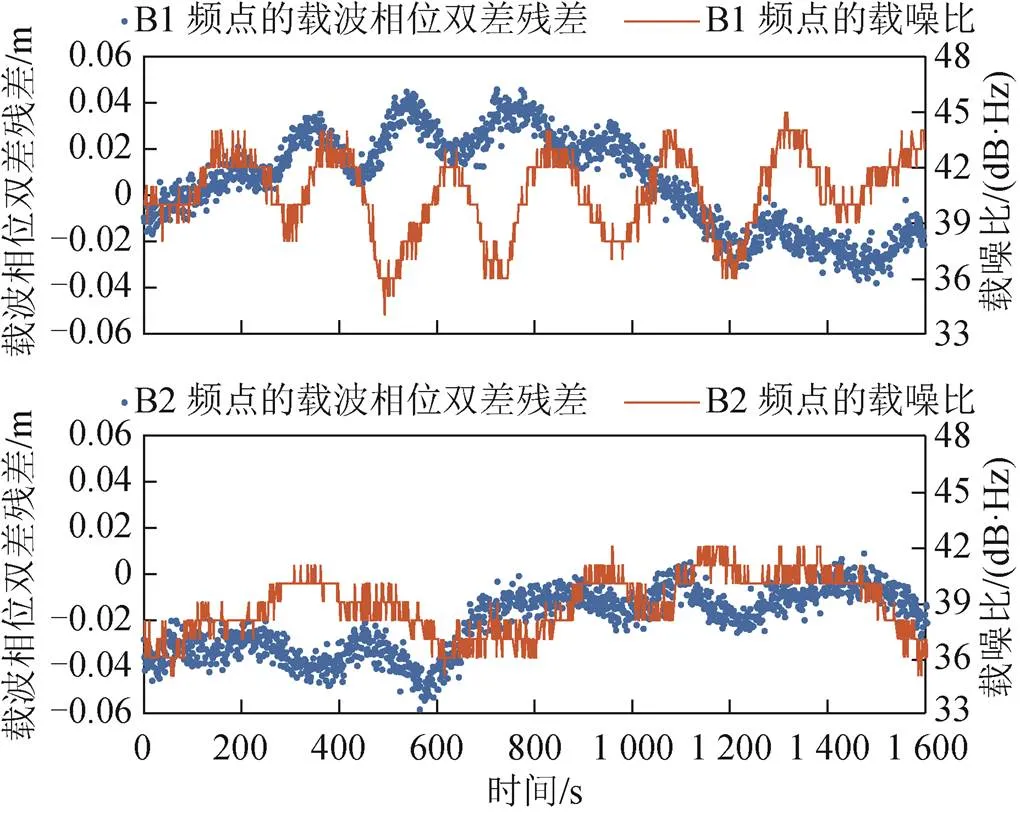
圖10 C16的載波相位雙差殘差和載噪比時間序列圖
2.4.3 高度角與載波相位雙差殘差相關性分析
圖11為C16的載波相位雙差殘差和高度角時間序列圖,由圖11可知,本次觀測時段內,BDS 16號星高度角逐步下降,但是,載波相位雙差殘差未隨之逐步下降,而是頻繁跳變。由此可見,高度角與載波相位雙差殘差間無明顯相關性。
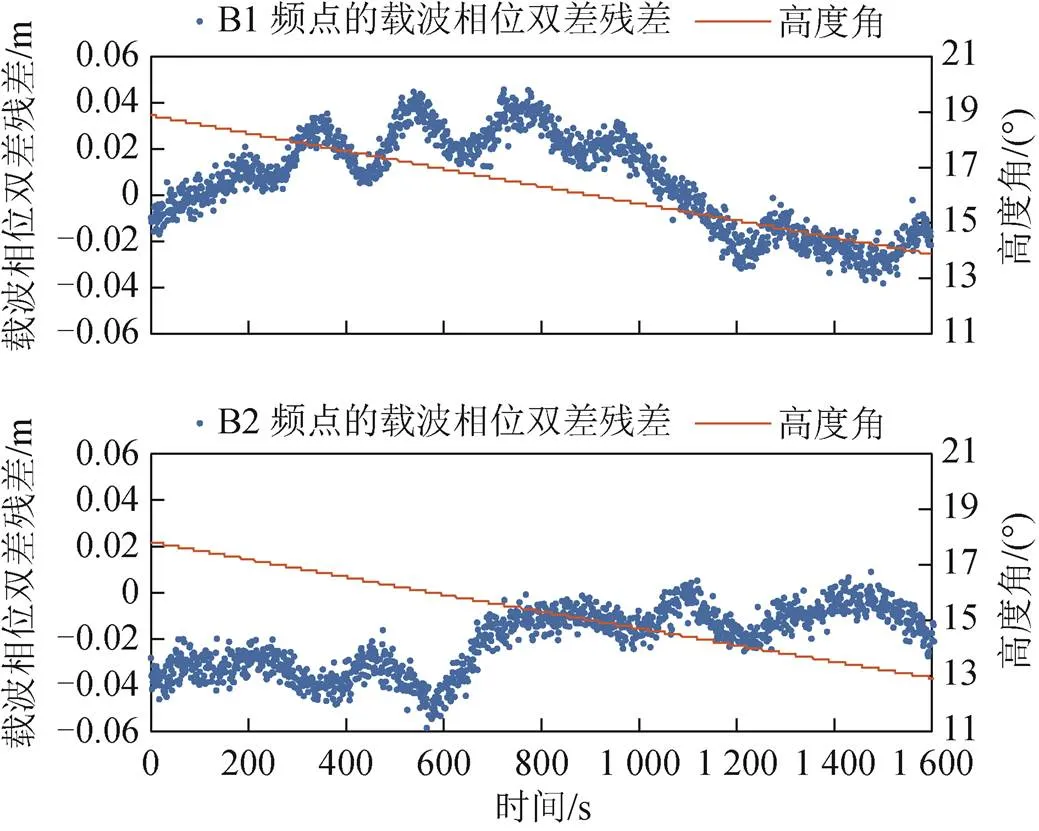
圖11 C16的載波相位雙差殘差和高度角時間序列圖
3 顧及RPLD的高度角指數函數隨機模型
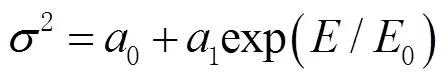

表2 指數函數模型相關系數的參考值
為評估該模型的性能,本文進行了動態和靜態試驗。在動態試驗時,將測試設備固定在汽車內,將GNSS接收機天線安裝在汽車車頂,汽車在高樓峽谷和林蔭道路中行駛;在靜態試驗時,則分別將GNSS接收機天線置于墻角和樹蔭環境中。動/靜態試驗的參考站均位于空曠的樓頂。本次試驗情況和異常觀測值占所有觀測值的百分比如表3所示。
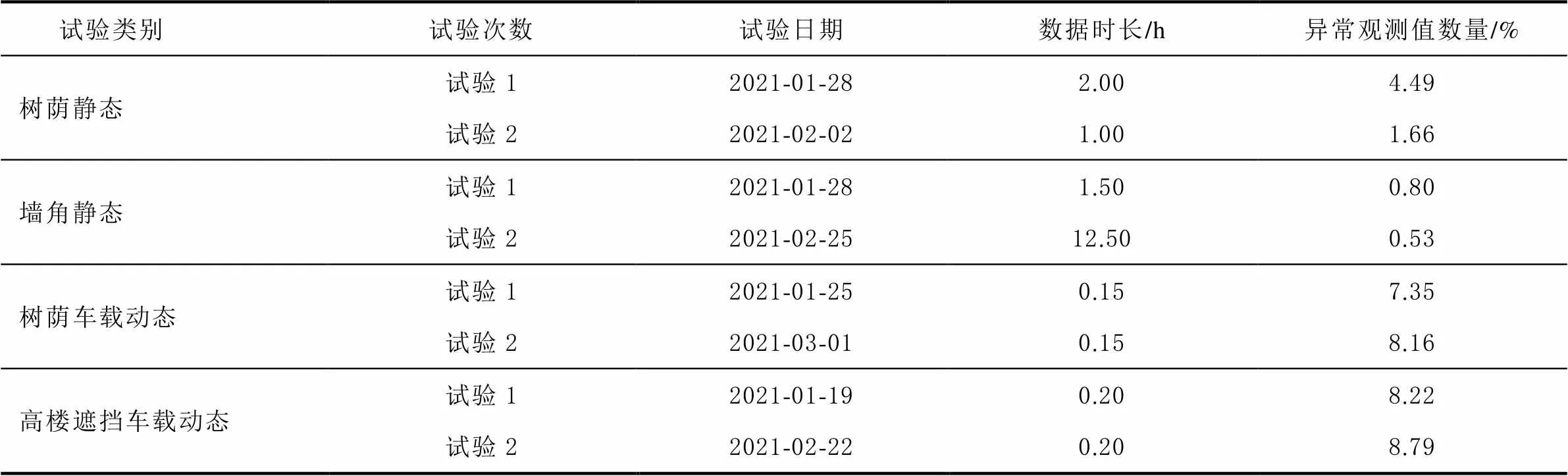
表3 試驗情況和異常觀測值數量匯總
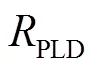
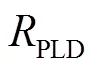
表4 使用前后的靜態相對定位誤差統計結果
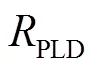
表5 使用前后的動態相對定位誤差統計結果
4 結束語
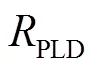
[1] CHEN X, LENZINI G, MARTINS M, et al. A trust framework for evaluating GNSS signal integrity[C]//The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Position Location and Navigation Symposium. Palms Springs: IEEE, 2013: 179-192[2021-09-26].
[2] ZHANG X, WU M, LIU W, et al. Initial assessment of the COMPASS/BeiDou-3: new-generation navigation signals[J]. Journal of Geodesy, 2017, 91(10): 1225-1240.
[3] HE Y. Quality analysis of signal for BDS-3 basic system[C]//Academic Exchange Center of China Satellite Navigation Office (CSNO). Proceedings of the 11th China Satellite Navigation Conference Symposium. Beijing: China Satellite Navigation Office, 2020: 506-516[2021-09-26].
[4] EUELER H J, Goad C C. On optimal filtering of GPS dual frequency observations without using orbit information[J]. Bulletin Géodésique, 1991, 65(2): 130-143.
[5] HARTINGER H, BRUNNER F K. Variances of GPS phase observations: the SIGMA-model[J]. GPS Solutions, 1999, 2(4): 35-43.
[6] BRUNNER F K, HARTINGER H, TROYER L. GPS signal diffraction modelling: the stochastic SIGMA-Δ model[J]. Journal of Geodesy, 1999, 73(5): 259-267.
[7] 張小紅, 丁樂樂. 北斗二代觀測值質量分析及隨機模型精化[J]. 武漢大學學報(信息科學版), 2013, 38(7): 832-835.
[8] 戴吾蛟, 丁曉利, 朱建軍. 基于觀測值質量指標的GPS觀測量隨機模型分析[J]. 武漢大學學報(信息科學版), 2008, 33(7): 718-722.
[9] 楊汀, 杜久升, 陳宜金. 基于衛星高度角模型的GNSS雙差觀測量方差估計[J]. 河南理工大學學報(自然科學版), 2017, 36(2): 63-67.
[10] JAMES J, SPILKER JR, AXELRAD P, et al. Global positioning system: theory and applications, volume I[M].Reston:American Institute of Aeronautics and Astronautics, 1996: 393-394.
[11] 謝鋼. GPS原理與接收機設計[M]. 北京: 電子工業出版社, 2017: 283.
[12] HAN S. Carrier phase-based long-range GPS kinematic positioning[D]. Sydney: University of New South Wales, 1997.
Quality analysis of GNSS observations and phase lock detector
PENG Hui1, DAI Wujiao1, YU Wenkun1, PAN Lin1, ZHENG Bin2
(1. School of Geosciences and Info-physics, Central South University, Changsha 410083, China 2. Hunan Bynav Technology Co. Ltd, Changsha 410083, China)
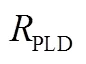
phase lock detector; global navigation satellite system; quality analysis; stochastic model
P228
A
2095-4999(2022)04-0115-10
彭會,戴吾蛟,余文坤,等. 相位鎖定指示值與GNSS觀測值質量分析[J]. 導航定位學報, 2022, 10(4): 115-123.(PENG Hui, DAI Wujiao, YU Wenkun, et al. Quality analysis of GNSS observations and phase lock detector[J]. Journal of Navigation and Positioning, 2022, 10(4): 115-123.)DOI:10.16547/j.cnki.10-1096.20220416.
2021-10-06
國家自然科學基金項目(41904030);湖南省自然資源廳科技項目經費資助項目(2021-24);中南大學研究生自由探索項目(2020zzts694)。
彭會(1997—),女,湖南常德人,碩士研究生,研究方向為導航定位與空間數據更新。
戴吾蛟(1977—),男,江西泰和人,博士,教授,研究方向為GNSS變形監測與變形分析。

