非均勻堤心石斜坡式防波堤透浪系數模擬研究

徐佳玲，趙劉群，馬玉祥，馬小舟

（1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧大連 116024；2.中交四航局第二工程有限公司，廣東廣州 510230）

引言

斜坡式防波堤的施工方法有陸上推進法和水上施工法，島式防波堤一般只能采用水上施工方案，施工時依照先下面后上面、先中間后兩邊的流程拋填石塊，在這個過程中水深、水流和波浪會對塊石的漂流產生影響。隨著斜坡堤高度增加，堤身水流斷面處的流速逐漸增大，對石塊的沖刷力度也逐漸增加。一般斜坡堤在粗填至接近靜水位時會選擇非大風大浪天氣一次性拋填到頂。秘魯錢凱海域的實際波浪參數統計結果表明，該海域長期受到長周期波作用，對堤心石的拋填產生不利影響。為保證施工進度，在非窗口期施工時擬采用較標準設計堤心石更大的石料作為堤心石使用。這樣會導致堤心石孔隙率增加，波浪可能更容易穿透防波堤，降低防波堤的波浪掩護效果。因此，需要對該新型結構在較長周期波作用下的過程進行模擬研究。

對于波浪與可滲透斜坡堤相互作用的研究方法有理論分析、物理模型試驗和數值模型試驗等。研究對象大多針對均質斜坡堤：葛曉丹(2013)[1]利用物理模型實驗的方法研究了均質斜坡堤在規則波或不規則波作用下的透浪系數的變化規律，并擬合出透浪系數公式；任增金(2003)[2]利用數值模型試驗的方法，從N-S方程出發，得出關于拋石防波堤中塊石最大受力的一般公式；Koley(2020)等[3]通過數值和物理試驗研究了三種不同結構高度和三種不同波高度的均質潛堤的波浪透射特性、反射特性和耗散特性。對于不均質斜坡堤，Garcia(2004)等[4]利用基于RANS方程的數值模型，研究了非均質潛堤在規則波和不規則波作用下的物理過程；楊會利(2019)等[5]利用物理模型試驗方法研究了非均質斜坡堤在規則波和不規則波作用下透射系數的變化規律。

目前對于斜坡堤透射采用物理模型試驗的方法居多，試驗時通常縮小尺寸進行研究，這種模型會產生比尺效應，建立原型模型會存在造價高昂、不符合實際等問題。本文利用OpenFOAM中的waves2Foam求解器對新型結構防波堤的波浪透射開展數值模擬，通過改變波高、新型結構堤心石的有效粒徑及范圍，分析不同工況下最大波高、有效波高及透射系數的變化規律，并嘗試擬合該新型結構對應的透浪系數公式，為進一步研究波浪透射提供科學依據。

1 數值模型

數值模型基于不可壓縮粘性流體的N-S方程。控制方程如下：

不可壓縮連續方程：

動量方程：

式中：u表示速度場；ρ表示整個流場的密度；μ表示動力粘性系數；p表示壓力；fσ表示自由面上的張力。

當開展波浪與多孔介質相互作用的研究時，需要將滲流運動的Darcy-Forchheimer方程導入到N-S方程，導入后的控制方程如下：

不可壓縮連續方程：

動量方程：

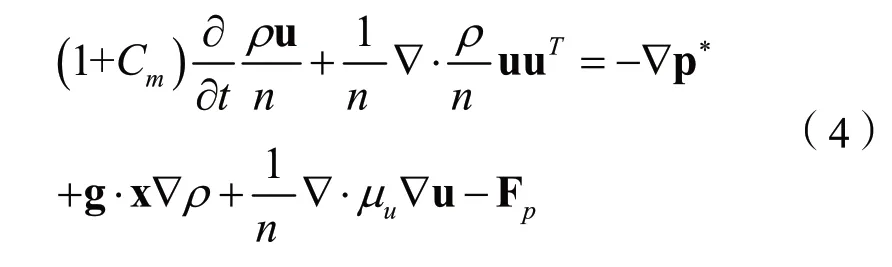
式中：u為笛卡爾坐標系中的速度矢量；Cm為增加的質量系數，γp作為經驗系數取0.34；t為時間；ρ為流體密度；n為可滲透結構的孔隙率；p*為動壓力；g為重力加速度；x=[x,y,z]為笛卡爾坐標向量；μu為速度場的動態粘度；Fp為來自可滲透結構的阻力，定義如下：

這里，a和b是由于線性和非線性流動阻力引起的阻力系數。Van Gent[6]通過參數化進行了描述：

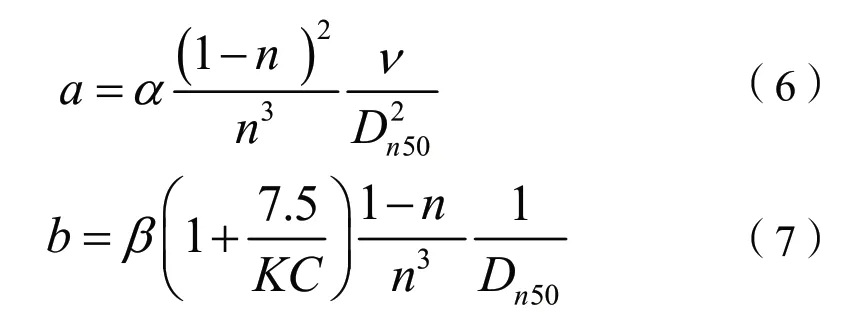
式中：α、β為經驗系數，Van Gent建議分別取1 000和1.1；v為運動分子粘度；Dn50為可滲透材料的中值粒徑；KC為Keulegan-Carpenter數。

模型利用VOF法解決自由表面的追蹤問題，方程式如下所示：

式中：ur為相對速度；F為VOF函數，當計算單元充滿水時，函數為1，當充滿空氣時，函數為0；中間值將位于界面或接近界面位置，采用以下流體特性的線性加權法：

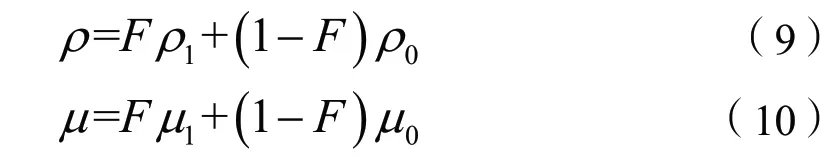
式中：下標1和0分別表示水和空氣的性質。

2 數值模型驗證

2.1 規則波透浪系數驗證

本文選擇文獻[1]的透射數據進行驗證。根據物理模型試驗的實際數據，建立長度為69 m，高度為1 m的二維數值水槽，水槽內的斜坡堤由均質堤心和擋浪胸墻組成，如圖1所示。堤心采用三種不同尺寸的均勻堤心石，不透水的擋浪胸墻保證無越浪條件。斜坡堤堤身前后坡度均為1:1.5，試驗斷面底部寬度分別為200 cm、250 cm、300 cm，高度分別為60 cm、70 cm、75 cm，物模試驗中在堤身前后放置了鐵絲網以防止堤心石散落。具體尺寸組合列于表1，其中堤寬B為堤心斷面在靜水位處對應的寬度，堤心石粒徑D是根據已知模型塊石質量按照球體體積公式計算得到的等效直徑，n為堤心孔隙率。

圖1 均勻介質斜坡式防波堤數值模型

表1 均勻介質斜坡式防波堤對應參數

選擇兩種規則波進行驗證：水深d為0.45 m，平均周期為3 s，平均波高分別為0.082 m、0.104 m。

斜坡堤放置在上游堤底距離入口35 m處。左側消波區長度取31 m，右側消波區長度取10 m。對浪高儀的位置按照文獻[1]內設計進行布置，堤前設置在距離入口32 m處，堤后設置在距離入口43 m和44.2 m處。波浪模擬時間取為50 s，可得到13～14個波。

首先，在水槽內沒有斜坡堤時進行造波模擬，取后兩個位置浪高儀的平均波高作為入射波高Hi。由圖2可得，當水槽內沒有斜坡堤，數值模擬得到的波面過程線與理論值相比比較吻合。

圖2 不同波高對應的波面過程線與理論值對比

當水槽內設置斜坡堤后，取堤后兩個浪高儀的平均波高作為透射波高Ht。透浪系數為透射波高與入射波高的比值，計算公式如下：

數模的透浪系數與文獻內的物模透浪系數對比如圖3所示，由圖3可知模擬效果良好。

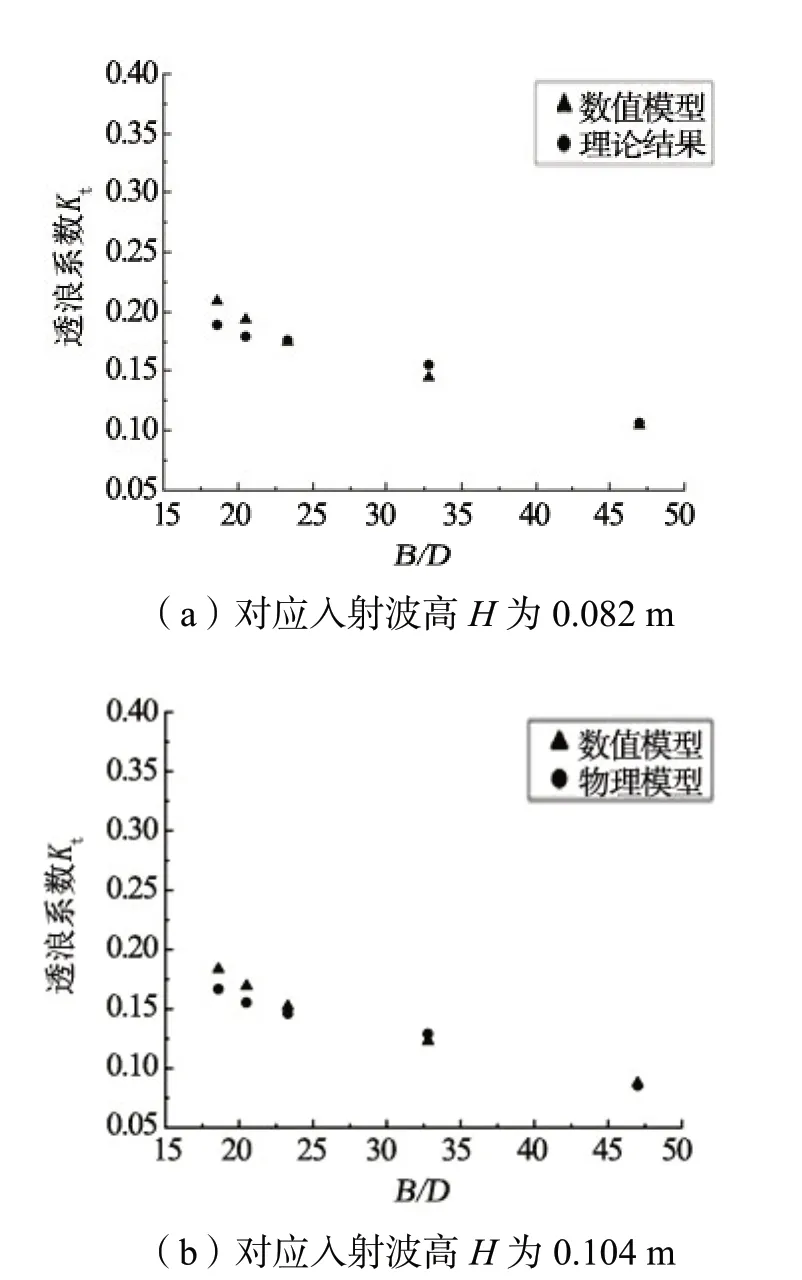
圖3 數值模型與物理模型透浪系數對比

2.2 不規則波透浪系數驗證

對于不規則波透浪系數驗證，依據王昊天[7]論文內透射數據，按照實際工程尺寸進行模擬。在數值模型內建立長度為1 500 m，高度為30 m的二維水槽，如圖4所示。

圖4 非均勻斜坡式防波堤數值模型

斜坡堤依據實際工程尺寸進行建模，包括堤心、墊層、護面層、胸墻等結構，各個結構的長度、高度等實際尺寸標于圖5，孔隙率、有效粒徑等參數列于表2，其中D50為材料的中值粒徑，n為孔隙率，胸墻為不透水材料。

圖5 實際非均勻斜坡式防波堤堤身斷面

表2 非均勻斜坡式防波堤參數設置

不規則波的頻譜采用合田改進的JONSWAP譜，譜峰因子γ取3.3，水深分別為16.8 m和18.6 m，有效波高分別為3.9 m和4.3 m，有效周期分別為18 s和20 s。具體參數組合列于表3。其中，d為水深，H1/3為有效波高，T1/3為有效周期。

表3 不規則波波況

將斜坡堤放置在距離入口850 m處，左側消波區長度取700 m，右側消波區長度取350 m。浪高儀設置在距離入口分別為750 m、950 m、1 000 m的位置處。模擬時間取2 000 s，可得到117～120個波。

當水槽中沒有斜坡堤時，取堤后950 m及1 000 m處有效波高的平均值為入射波高Hi。放入斜坡堤后，相同位置處的平均值為透射波高Ht。數值模擬的透浪系數與文獻內的數據對比如圖6所示。由圖6可得，前三種波況擬合良好，波況2、3得到的透浪系數完全一致。對于波況4，由于文獻中物模試驗沒有發生越浪，而數值模擬時發生越浪，導致數模透浪系數偏大。因此當不發生越浪情況時，數值模型的模擬效果良好。

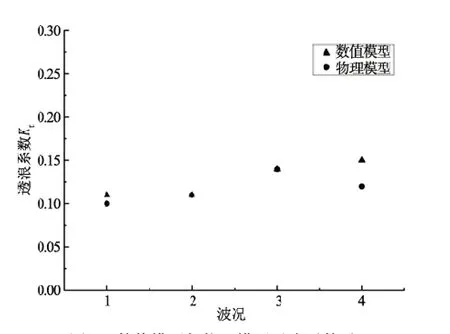
圖6 數值模型與物理模型透浪系數對比

3 新型結構斜坡堤的透浪模擬

為解決施工過程中堤心石的成型率問題，設計了一種新型的斜坡堤結構，如圖7所示，與不規則波驗證算例用到的斜坡堤相比：堤心部分區域的材料由1～500 kg開山石換成粒徑更大的材料；堤底所在的高度從-17 m提高到-16 m，位于更靠近岸邊位置。二維數值水槽長1 500 m，高30m，按照實際尺寸對新型斜坡堤進行建模，放置在距離入口850 m處，左側消波區長度取700 m，右側消波區長度取350 m。浪高儀設置在距離入口分別為750 m、950 m、1 000 m的位置處。

3.1 堤心石粒徑變化對新型斜坡堤透射影響

首先研究堤心石粒徑不同時對應的新型斜坡堤的透射變化。保持斜坡堤各個結構的尺寸與圖7內所示不變，大尺寸堤心石區域的厚度為8 m，堤心區域、墊層和護面層的孔隙率及中值粒徑與表2內所示不變。大尺寸堤心石區域材料的粒徑依據實際塊石粒徑取五種，參數列于表4，其中D50為材料的中值粒徑，n為孔隙率。對于工況1，材料的中值粒徑與原堤心材料的相同，相當于不設置大尺寸區域；對于工況5，材料的中值粒徑與墊層相同。隨著中值粒徑的增大，假設孔隙率也隨之增大，孔隙率按照線性插值的方法得到。

圖7 新型的非均勻斜坡式防波堤斷面

表4 大尺寸堤心石處參數設置

按照工程實際，對斜坡堤施加不規則波進行模擬，不規則波的水深為17.6 m，有效波高為3.9 m，有效周期為18 s，頻譜采用合田改進的JONSWAP譜，譜峰因子γ取3.3。模擬時間取2 000 s，可以得到119～130個波。

模擬結果如圖8、圖9所示，其中圖8為大尺寸堤心石區域不同有效粒徑對應的各類波高，Hmax表示最大波高，取950 m、1 000 m兩個位置浪高儀測得的最大值，H1/3表示有效波高，取兩個位置浪高儀測得的平均值；圖9為對應透浪系數，計算方法與驗證不規則波時的方法相同。

由圖8可得，有效波高隨大尺寸堤心石區域有效粒徑的增大而增大。前兩組結果相比，最大波高并沒有隨有效粒徑的增大而增大，工況1、2的最大波高相差0.0307 m，可能是由于兩個工況中存在測量時間節點與波面過程線的最值沒有重合所導致；后四組結果相比，最大波高隨著有效粒徑的增大而增大，但增大的趨勢逐漸放緩。最大波高中的最小值為工況2得到的0.7367 m，最大值為工況5得到的0.8826 m，兩者相差0.1459 m。由圖9可得，將部分堤心區域的粒徑換成較大尺寸的石塊，透浪系數會有明顯增大；且隨著大尺寸堤心石區域的有效粒徑的增大，透浪系數逐漸增大；后四組相比，透浪系數的增加趨勢也逐漸放緩。

圖8 不同有效粒徑對應波高變化

圖9 不同有效粒徑對應透浪系數

3.2 入射波高變化對新型斜坡堤透射的影響

研究不同入射波高作用下新型斜坡堤的透射變化時，斜坡堤保持不變。按照圖7進行建模，大尺寸堤心石區域的厚度為8 m，材料為900～2 700 kg塊石，孔隙率及中值粒徑與墊層材料的參數相同，其他材料的孔隙率與中值粒徑見表2。

波況依據秘魯錢凱多功能碼頭（一期）所在工程區域處的實際情況進行設置，選擇不同重現期的不規則波波況，頻譜采用合田改進的JONSWAP譜，譜峰因子γ取3.3，具體波高變化列于表5。其中，d為水深，H1/3為有效波高，T1/3為有效周期。模擬2 000 s，可得到126～132個波。

表5 不規則波波況

由圖10可得，隨著入射波高的增大，最大波高及有效波高逐漸增大，平均波高的增長趨勢比較穩定；最大波高的前四組以大約0.05 m的幅度逐漸增大，最后兩組相比，最大波高的增幅增大至0.16 m。由圖11可得，斜坡堤保持不變時，透浪系數隨著入射波高的增大而降低，且降低幅度逐漸放緩。

圖10 不同入射波高對應波高變化

圖11 不同入射波高對應透浪系數

3.3 厚度變化對新型斜坡堤透射的影響

當研究大尺寸堤心石區域厚度對波浪透射的影響時，保持墊層、護面層及擋浪胸墻的尺寸及參數不變，大尺寸堤心石區域的材料保持不變，設置為900～2 700 kg塊石，孔隙率及中值粒徑與墊層材料的參數相同，具體數值見表2。改變大尺寸堤心石區域靜水位以下厚度，大尺寸堤心石區域的上底長度、位置及兩側坡度不變，根據圖7所示的新型斜坡堤斷面設置，梯形下底的高度從-4m逐漸升高至-2 m，各個工況設置如表6所示。

表6 大尺寸堤心石區域對應不同厚度

對以上工況，施加水深為17.6 m，有效波高為3.9 m，周期為18 s的不規則波，頻譜采用合田改進的JONSWAP譜，譜峰因子γ取3.3。模擬時間取2 000 s，可以得到119～130個波。

由圖12可得，隨著大尺寸堤心石區域的厚度逐漸增加，最大波高及有效波高都逐漸增大；但是增加的幅度并不大，從厚度為2.5 m增大至4.5 m，最大波高的增幅為0.0757 m。由圖13可得，透浪系數隨著該區域厚度的增加而增大。

圖12 大尺寸堤心石處不同厚度對應波高變化

圖13 大尺寸堤心石處不同厚度對應透浪系數

4 新型結構斜坡堤的透浪系數公式擬合

其中a、b、c為待定系數。

根據以上假設公式，針對本文研究的新型斜坡堤，對參數B、D、d進行變換以滿足復雜結構斜坡堤的特點，變換如公式(13)～(15)所示：

式中：代表不同結構靜水位處的寬度；D*代表不同材料的中值粒徑，下標1、2、3、4分別對應堤心、大尺寸堤心石區域、墊層、護面層。

式中：代表靜水位以下各部分斷面面積，下標1、2、3、4分別對應堤心、大尺寸堤心石區域、墊層、護面層；S0代表整個斜坡堤水下部分的斷面面積。

式中：d1為大尺寸堤心石下底距離斜坡堤底部的高度；d2為大尺寸堤心石底部距離靜水位的高度；由于墊層及護面層的厚度相對較小，假定忽略兩者對水深d的影響。

依據新的公式及以上十五組工況擬合得系數分別為a=0.8、b=0.61、c=-0.07。

數值模擬的透浪系數與公式擬合出的計算值的對比情況如圖14所示。數值模擬出的透浪系數與計算值的相關系數為0.839。數值模擬出的透浪系數與計算值相差最大的三組情況出現在工況1、2、3，當大尺寸堤心石區域的有效粒徑與原堤心石的有效粒徑相近時，公式得到的計算值大于數值模型模擬值，結果偏安全；當大尺寸堤心石區域的有效粒徑與墊層區域的有效粒徑相近時，計算值與數模值擬合效果良好。

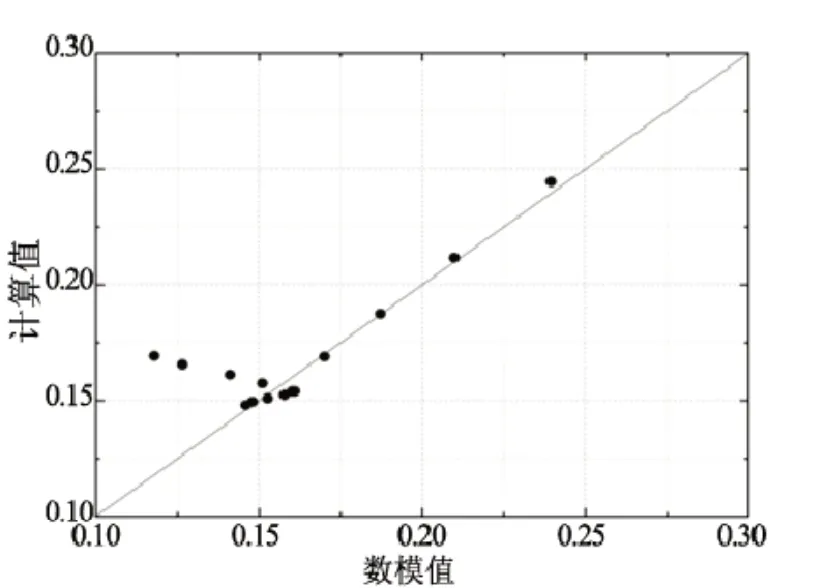
圖14 透浪系數數值模擬值與公式計算值的比較

針對新公式，設計新的工況進行數值模擬，數模結果與公式的計算值進行對比，工況組合列于表7。其中，厚度表示大尺寸堤心石處在靜水位以下的厚度，工況1～5及工況10～14分別為大尺寸堤心石處靜水位以下厚度為2.5 m和3.5 m、且材料的有效粒徑保持不變時，不規則波的波高發生變化；工況6～9及工況15～18分別為大尺寸堤心石處靜水位以下厚度為2.5 m和3.5 m、且不規則波的波高不變時，有效粒徑發生變化。

表7 新型斜坡式防波堤對應工況

數值模擬的透浪系數與公式擬合出的計算值的對比情況如圖15所示，兩者的相關系數為0.9149；圖中數模值與計算值相差較大的情況也是出現在有效粒徑為0.45 m和0.6041 m時的工況，計算值偏安全。因此文章得到的公式精度還需要進一步提高，而目前得到的結果偏安全，也具有一定的參考價值。

5 結語

本文基于秘魯錢凱港海域的斜坡式防波堤施工過程中面臨的實際工程需求，利用OpenFOAM中的waves2Foam求解器研究了不規則波波高、大尺寸堤心石的有效粒徑及厚度對透射系數的影響，得到以下結論：

1）文中的新型結構斜坡堤嘗試將堤心位置處的部分材料換成尺寸更大的，以便更順利的完成拋填過程。由模擬可得，當大尺寸堤心石區域的有效粒徑或者厚度增大時，最大波高、有效波高及透浪系數也逐漸增大；當入射波高逐漸增大時，最大波高、有效波高隨之增大，而透浪系數逐漸減小。

2）對復雜結構的新型斜坡堤，擬合出了一個新的透浪系數公式，并對公式進行了驗證。結果表明，在給出的有效粒徑范圍內，當大尺寸堤心石區域的粒徑偏大時，公式的擬合效果較好；大尺寸堤心石區域的粒徑偏小時，公式計算的結果偏安全。