冰-車-橋系統耦合振動分析

吳甜宇， 邱文亮

(1. 重慶交通大學 省部共建山區橋梁及隧道工程國家重點實驗室， 重慶 400074;2. 大連理工大學 建設工程學部， 大連 116024)

渤海是我國緯度最低的結冰海域，冬季及初春開化時期會形成特有的流冰現象，渤海海域跨海橋梁的建設與運營將面臨冰荷載的嚴峻挑戰。因此，橋梁結構在車輛和冰荷載共同作用下的振動分析以及行車安全分析已成為寒區結冰海域橋梁建設不可回避的研究課題。

隨著橋梁跨徑的增大和汽車軸重的增加，公路橋梁上的車-橋相互作用問題越來越突出。自20世紀70年代以來，隨著有限元方法的發展和計算機在土木工程中的應用，車-橋相互作用理論已經發展到包括復雜的車輛模型、橋梁模型以及路面粗糙度模型。對于車-橋耦合研究方向的發展歷程來看，學者們提出了許多模型研究交互系統的動態響應。Yang等[1]采用結構動力縮聚方法將車輛的自由度縮聚到相應的橋梁上，從而求解車-橋相互作用系統的積分方程。該法是計算橋梁響應的有效方法，但它不足以計算車輛響應。Neves等[2]開發了一種有效的車-橋耦合計算方法，在該算法中車輛和橋梁的控制方程與附加的約束方程相互補充，約束方程實現了車輛接觸節點位移與橋梁相應節點位移的耦合作用。Lu等[3]利用罰函數定義車橋接觸條件，提出了基于有限元軟件ABAQUS的車-橋相互作用系統的動力分析框架，實現了車-橋相互作用的仿真模擬。通過對比分析，發現數值結果與Yang等[4]提出的經典車-橋相互作用問題的解析解吻合很好，證明了該方法的正確性。

此外，許多研究學者對考慮不同影響因素的車-橋耦合振動分析開展了針對性的研究。夏超逸等[5-6]建立了撞擊荷載作用下的車-橋耦合系統動力分析模型，提出了一種適用于車-橋動力耦合系統的時程積分全過程迭代法，系統地研究了撞擊荷載類型、撞擊強度、列車速度等對橋上列車運行安全指標的影響規律，給出了撞擊荷載作用下保障橋上列車運行安全的撞擊強度-列車速度閾值曲線的確定方法。喬宏等[7]基于子結構方法，將完整的列車-橋梁-樁基-地基相互作用模型分解為列車-橋梁相互作用子系統和樁基礎相互作用子系統，研究了樁土相互作用對車橋耦合系統動力響應的影響。謝娟娟等[8]建立了隨機汽車-橋梁耦合模型，采用路面譜對路面不平順進行模擬轉換，引入概率密度演化方法，對考慮路面不平順隨機性的汽車過橋動力響應進行了分析。Camara等[9]提出了考慮橋面粗糙度隨機特性的風-車-橋耦合分析框架，進行了風荷載作用下橋上行車安全性及行車舒適性風險分析。Li等[10]研究了地震作用下高墩連續鋼構橋梁車-橋相互作用系統的動力反應，探討了地震動、地面峰值加速度值、橋墩高度、車速等參數對車輛和橋梁動力響應的影響。

綜上所述，雖然目前車-橋耦合振動分析已經取得了較多的研究成果，但是對于冰荷載作用下的車-橋耦合振動研究還比較缺乏。因此，本文提出了冰-車-橋系統耦合動力分析框架，系統的研究了冰荷載作用下橋梁和車輛的動力反應，分析了不同車速和冰速對橋上行車安全的影響。本文研究成果可為冰荷載作用下寒區海域跨海橋梁的行車安全評估提供參考。

1 冰-車-橋系統耦合動力分析框架

1.1 車輛模型

本文采用的車輛模型是典型的兩軸六輪載重卡車，每輛卡車都被視為一個具有12個自由度的動力學系統，其中車輛模型為一個質量-彈簧-阻尼體系，包含一個車體和兩個輪軸，前輪軸包括一個輪對，后輪軸包括兩個輪對，如圖1所示。車輛懸掛系統和車輪采用彈簧進行建模，利用黏滯阻尼模擬懸掛和車輪的能量耗散過程，懸掛和車輪的質量均集中在車體的質量上，卡車特征參數詳見文獻[11]。卡車模型的動力學系統可以利用下面的廣義位移矢量進行表示

wv={zv11yv11θvy11θvx11θvz11zv12yv12θvx12zv22θvy12yv22θvx22}

(1)

式中：zv11,yv11,θvy11,θvx11和θvz11分別為車體的豎向位移、橫向位移、俯仰角、轉動角和平擺角；zv12,yv12和θvx12分別為車體前軸的豎向位移、橫向位移和轉動角；zv22,θvy12,yv22和θvx22分別為車輛后軸的豎向位移、俯仰角、橫向位移和轉動角。

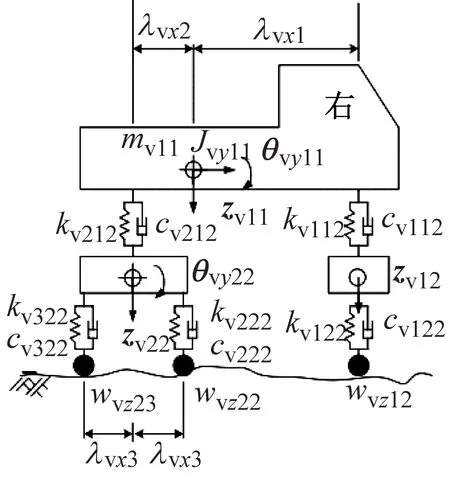
圖1 具有12個自由度的卡車模型示意圖

1.2 橋梁模型

本文采用秦皇島-大連跨海通道的非通航孔橋梁設計方案為研究對象，該橋梁設計方案為典型的高樁承臺群樁基礎結構型式，如圖2(a)所示。圖2(a)中MWL為平均海平面。橋梁上部結構采用5×120 m一聯的連續鋼箱梁，主梁頂面寬度為33.5 m，設置雙向6車道，如圖2(b)所示。橋梁下部結構采用鋼管打入樁基礎，鋼筋混凝土橋墩為圓端空心墩，平面尺寸為3.5 m×10.0 m，壁厚為0.8 m。鋼筋混凝土承臺的平面尺寸為13.0 m×21.0 m×6.0 m，承臺底部與13根直徑為2.0 m的鋼管打入樁連接。

為了充分考慮上部結構跨度之間的偶聯效應，建立跨度為1 800 m的三聯連續梁橋進行分析。將主梁建模為空間板單元，橋墩、承臺以及鋼管打入樁基礎采用三維梁單元。動水壓力通過附加水質量進行考慮，并施加在相應的水下樁柱節點位置。采用p-y曲線、t-z曲線和Q-z曲線計算土體對樁的橫向、豎向和基底非線性約束剛度。利用瑞利阻尼對橋梁結構進行建模，瑞利阻尼系數對應于前兩階橋梁振型下的1%阻尼比。

需要說明，由于橋梁設計水位在承臺底面處，冰荷載將直接作用于大尺度承臺上。冰荷載的作用方式為各承臺一致激勵。上述所有模型全部集成于ABAQUS軟件數值模擬平臺，并借助二次開發進行研究。

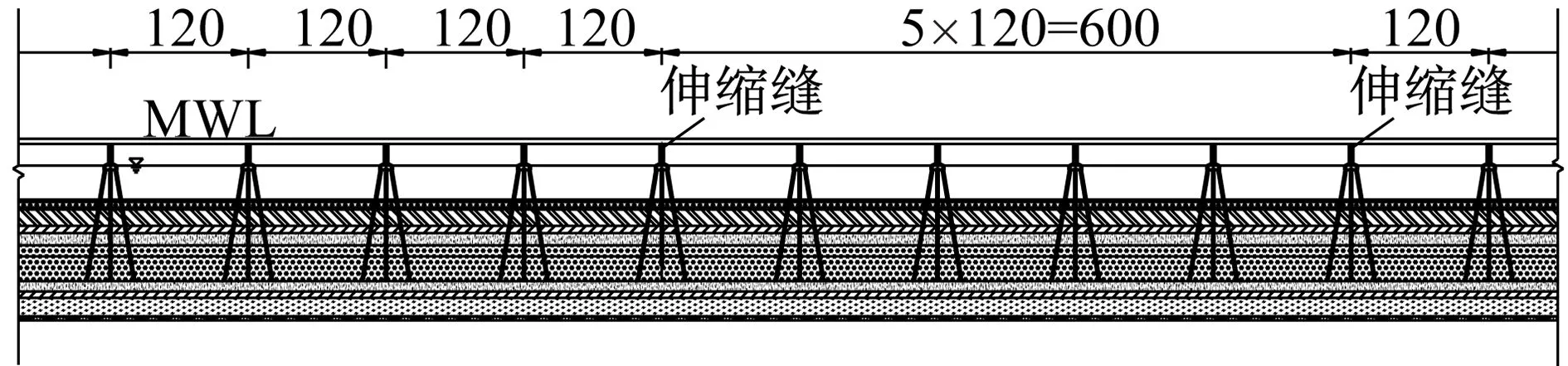
(a) 橋梁立面圖

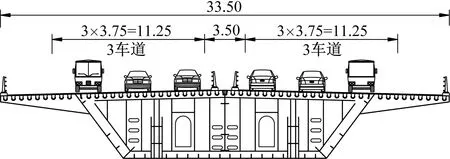
(b) 主梁截面

1.3 接觸模型

在接觸問題的研究中，罰函數法是一種解決約束優化問題行之有效的方法[12]。接觸問題的約束方程可以表示為

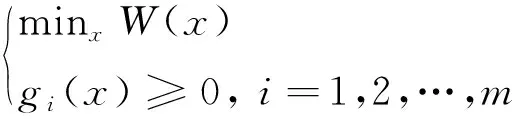
(2)

式中：W(x)為目標函數；gi(x)為約束條件為x的函數。為了使目標函數W(x)最小，引入罰函數使得約束優化轉化為無約束優化，轉化后的約束方程可以表示為

(3)

式中：G[gi(x)]為罰函數；rk為罰函數的參數；m為約束條件數。

結構方程組由虛功原理導出，而虛功原理又由最小勢能原理導出。實踐證明，罰函數法可以轉化為最小勢能原理[13]。因此，如果以勢能為目標函數，以接觸情況為約束條件，如式(3)所示，罰函數方法是適用于接觸問題的。

(4)

式中：Πp為整個系統的勢能；gi(u)為接觸面積上的間隙函數，它是接觸點之間距離u的函數。

罰函數法在有限單元中的應用思想是在接觸體之間增設虛擬彈簧，允許接觸對象之間的虛擬假設。實際上，gi(u)在數值上可以是正的，也可以是負的，相應的正負值分別代表分離和接觸機制。將虛彈性勢能項引入式(4)中，勢能函數的一般原理可以改寫為

(5)

式中：Πp(u)為系統的勢能；G[gi(u)]為罰函數。

研究結果表明[14]，無論是在靜力分析還是動力分析情況下，對于分離、滑動及摩擦等接觸問題，應用罰函數方法開展的數值計算都能得到比較精確的結果。因此，本研究利用罰函數定義了車輪與橋面之間的接觸關系，將車輪與橋面的相互作用設置成硬接觸，從而允許兩者發生分離。

1.4 路面粗糙度

路面粗糙度是近似的高斯平穩隨機過程[15]，為了簡化對路面粗糙度的描述，國際標準ISO-8608[16]給出了模擬路面粗糙度的簡化功率譜密度函數，可以表示為

(6)

式中：η為空間頻率；η0為0.1cycle/m的參考頻率；φ(η0)為粗糙度系數，m3/cycle，其值取決于路面狀況。

假定路面粗糙度是一個零均值的平穩高斯隨機過程。因此，路面粗糙度函數r(x)可以通過傅里葉逆變換得到，可以表示為

(7)

式中：θk為相位角，在0～2π變化；n為波數，cycle/m;N為模擬的點數;φ(nk)為路面粗糙度的功率譜密度函數;nk為第k點的波數，cycle/m。

本文根據國際標準ISO-8608中的規定，模擬了粗糙度系數為φ(n0)=20×10-6m3/cycle的等級“良好”的路面粗糙度平穩高斯隨機過程，如圖3所示。

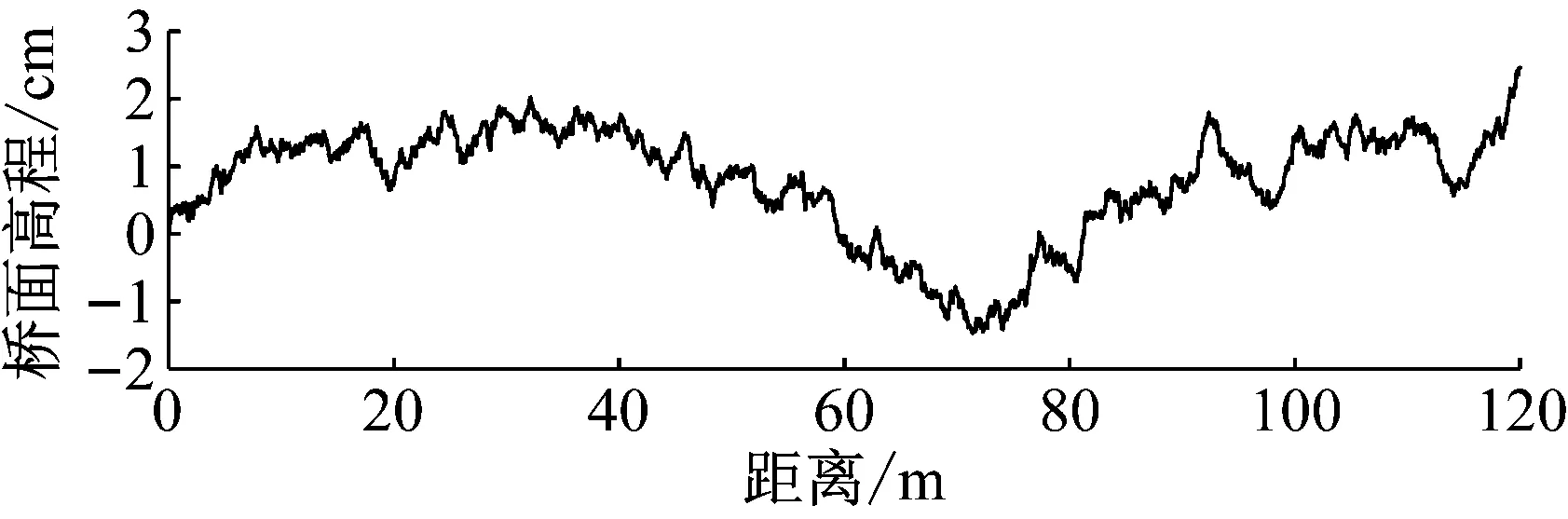
圖3 路面粗糙度隨機過程

1.5 自激冰力模型

為了實現數值計算，通常將冰體擠壓強度與應力速率表達式分段線性化，如圖4所示。線性化后，冰體擠壓強度與應力速率的多線性關系可近似為

(8)

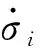
圖4 冰體擠壓強度與應力速率的多線性關系

M??tt?nen[17]給出了冰體發生擠壓破碎過程中的應力速率與相對速度的表達式

(9)

式中：D為結構直徑；σc為冰體最大擠壓強度；Vr為冰與結構相對速度。

對圓形承臺截面的局部冰應力在-π/2～π/2內進行積分來獲得結構整體冰力，如圖5所示。局部冰應力還應包括徑向正應力分量和切向剪應力分量。結構總冰力可表示為

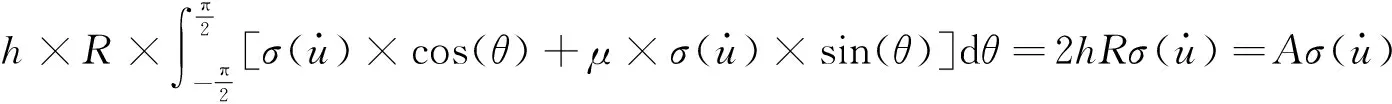
(10)

聯立式(8)和式(9)，結構總冰力可以改寫為

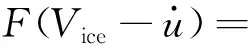
(11)

式中，Vice為冰速。

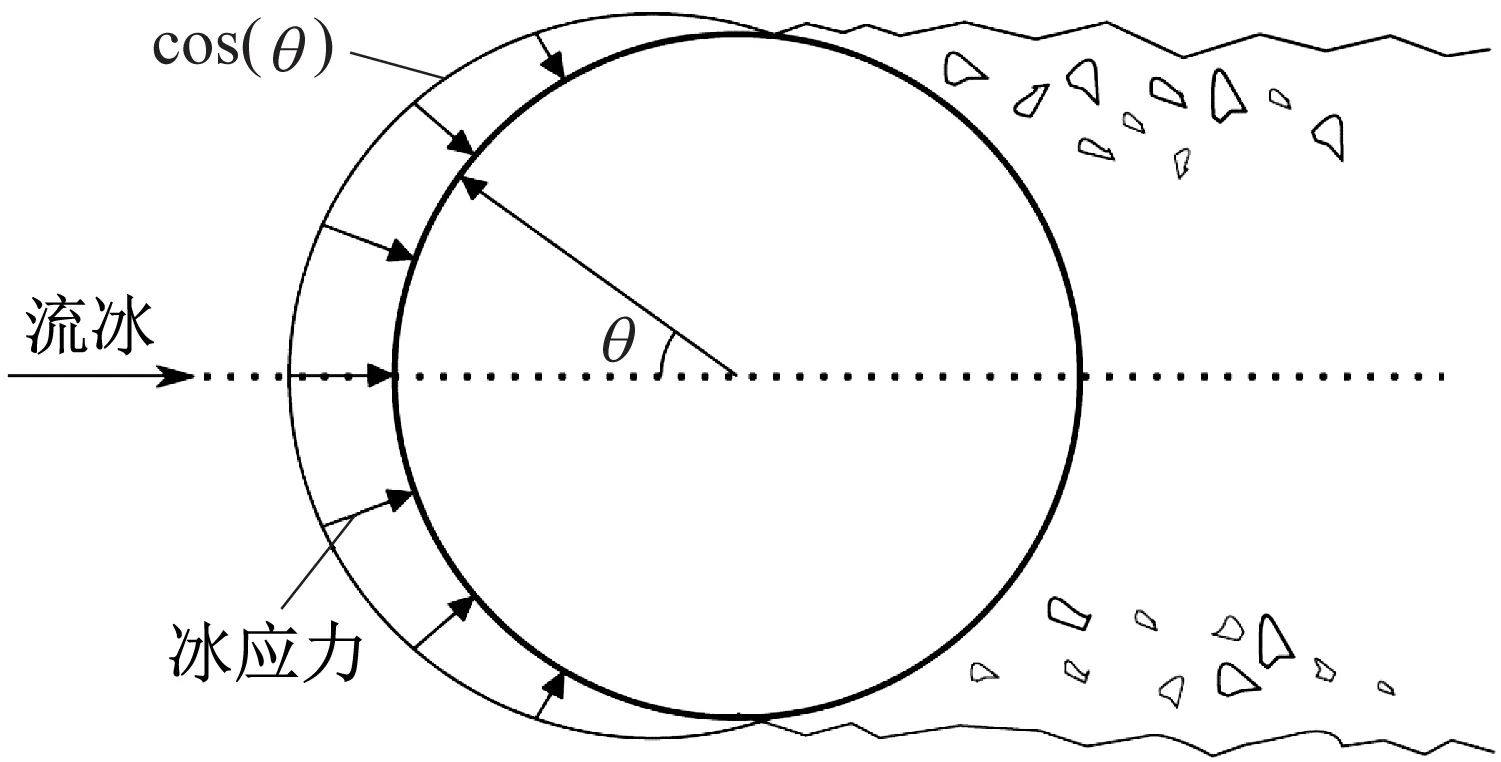
圖5 圓形結構上的冰應力分布示意圖

其中，僅與冰速有關的冰力部分，可表示為

(12)

結構體系中新的阻尼系數可以表示為

(13)

式中，C為結構原始阻尼。

對于線性化模型，可按冰體應力速率分為3個分段函數進行冰力模擬，可以寫為

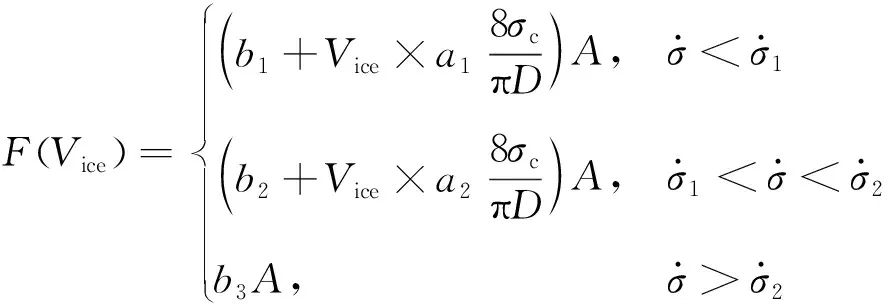
(14)

阻尼系數隨著冰體應力速率而變化，其分段表達式可以寫為

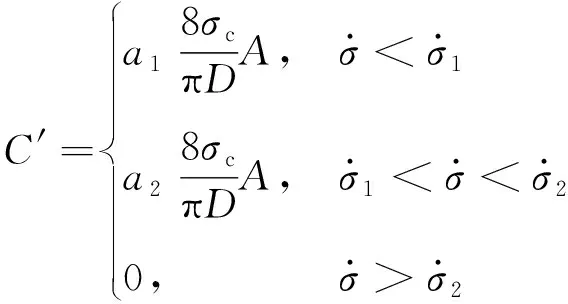
(15)

1.6 冰-車-橋系統耦合動力方程

考慮水下橋梁樁基礎的動水壓力以及樁-土之間的相互作用，建立了包括附加水質量和非線性土彈簧的冰-車-橋系統的耦合動力方程，可以表示為

(16)

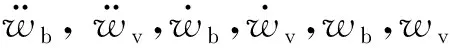
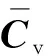
外力項Fbb包括兩部分：① 車體重力，其大小保持不變，但隨著車輛的移動其加載位置不斷變化；② 車-橋相互作用力，包括車輛懸掛系統的彈簧力和阻尼力，取決于車輛和橋梁的動力響應。因此，相互作用力總是隨著車輛移動而時變。同樣，外力項Fvv由車-橋相互作用力產生，Fice為只與冰速相關的冰力項。

2 冰-車-橋系統耦合振動分析

2.1 工況設置

基于國際重型卡車速度限制的要求[18]，標準卡車行駛速度一般為70 km/h。此外，選取40 km/h和100 km/h的車輛速度作為車輛行駛中的低速和高速進行對比分析。在實際道路交通中，不同駕駛員保持的車頭時距會有顯著差別，同一個駕駛員保持的車頭時距也會隨著個人狀態和環境影響而發生變化。本文采用的車頭間距按照國際上規定的兩秒定律[19]，兩輛相鄰車輛之間的最小安全間距由車速乘以2 s來估計，即：最短車頭時距取2 s左右的行程。為了滿足安全行車條件下的最小安全間距，將不同車速工況下的行車距離設置為55 m (2 s×100 km/h)，39 m (2 s×70km/h)，22 m (2 s×40 km/h)的均勻間距。為了模擬真實的車流情況，本研究假設共有18輛車在橋梁左幅的3條車道上行駛，每條車道上等間距的設置6輛車作為考慮的車輛流進行分析。

采用全橋模型的中跨跨中點作為橋梁結構反應測點進行橋梁振動分析，將車流中的第一輛車(頭車)作為目標車輛進行車輛振動及行車安全研究。本文還考慮了不同冰速的影響。冰速選取vi1= 0.6 m/s，vi2= 0.8 m/s和vi3= 1.0 m/s作為慢、中、快冰速進行對比分析。冰厚取為0.46 m(五十年一遇設計單層冰冰厚)，海冰擠壓強度取為2.15 MPa(五十年一遇設計海冰強度)[20]。

2.2 橋梁振動分析

車輛以3種不同的行駛速度通過橋梁時，在冰速為1.0 m/s的情況下橋梁跨中測點的豎向位移反應情況，如圖6所示。為了便于觀察，橫坐標設置為vvt/L。其中：vv為車速；t為車輛行駛時間；L為橋梁跨度。由圖6可知，隨著車輛行駛速度的增加，橋梁豎向位移反應具有增大的趨勢。例如，車輛行駛速度為100 km/h的橋梁最大豎向位移比行駛速度為40 km/h的增加了20%。這是因為橋梁的豎向位移反應主要是由車體自質量所引起的，由于橋面粗糙度的作用，車輛行駛速度越快，車-橋相互作用力越大，從而引起了更大的橋梁豎向位移。當車輛以100 km/h的行駛速度通過橋梁時，在3種不同冰速的情況下橋梁跨中測點的豎向位移反應情況，如圖7所示。由圖7可知，冰荷載的作用對于橋梁的豎向位移反應影響很小，這是因為冰荷載的作用方向是沿著橋梁橫向施加的，這與不考慮動冰荷載作用下的車-橋耦合振動研究結果相似[21]。

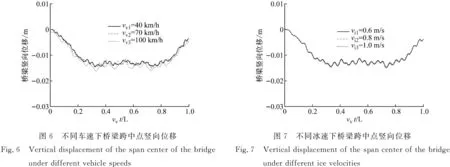
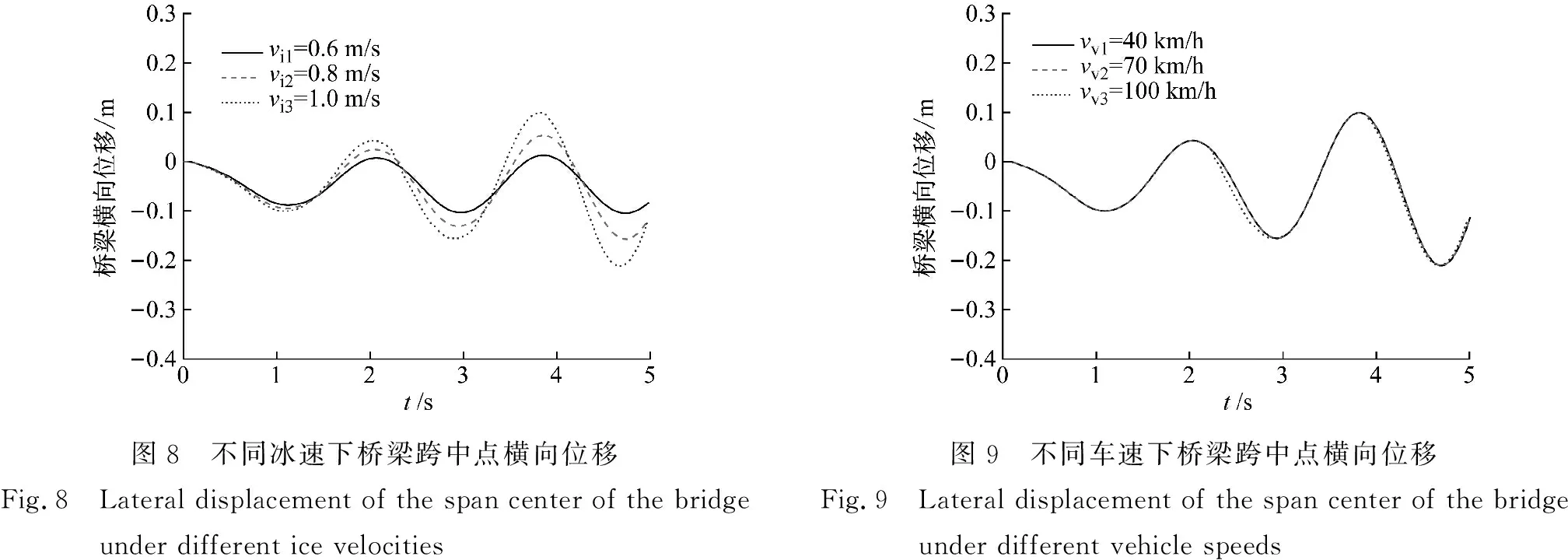
當車輛以100 km/h的行駛速度通過橋梁時，3種不同冰速情況下橋梁跨中測點的橫向位移反應情況，如圖8所示。由圖8可知，橋梁的橫向位移反應明顯受到了不同冰速的影響。隨著冰速的增大，橋梁的橫向位移反應具有明顯增大的趨勢。例如，當冰速從0.6 m/s增加到1.0 m/s時，橋梁的最大橫向位移從0.104 m增加到0.211 m，相比增長125%。這說明快冰速會增大冰與橋梁結構的相互作用力，進而引起更大的橋梁振動。當車輛以3種不同的行駛速度通過橋梁時，在冰速為1.0 m/s的情況下橋梁跨中測點的橫向位移反應情況，如圖9所示。由圖9可知，車速的變化對于橋梁的橫向位移反應影響不大，這是由于車輛在行駛過程中車體的振動只在豎向上影響橋梁，對于橋梁的橫向動力反應貢獻很小。

2.3 車輛振動分析

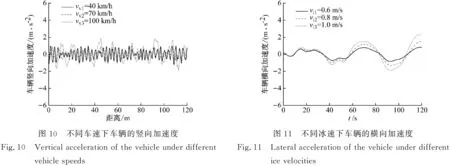
當車輛以3種不同的行駛速度通過橋梁時，在冰速為1.0 m/s的情況下車輛的豎向加速度反應情況，如圖10所示。由圖10可知，隨著車速的增加，車輛的豎向加速度反應具有明顯增大的趨勢。例如，當車速為40 km/h，70 km/h和100 km/h時，車輛的最大豎向加速度分別為0.84 m/s2，1.08 m/s2和1.89 m/s2。這是因為由于路面粗糙度的作用，車輛在高速行駛的過程中產生了更大的車-橋相互作用力，進而引起了更大的車輛豎向振動。此外，由2.2節可知，不同冰速僅對橋梁的豎向位移產生了輕微的影響。可以預見，冰速的變化對車體豎向振動反應影響不大，故本節不再贅述。

當車輛以100 km/h的行駛速度通過橋梁時，3種不同冰速情況下車輛的橫向加速度反應情況，如圖11所示。由圖11可知，隨著冰速的增加，車輛的橫向加速度反應呈現明顯增大的趨勢。例如，當冰速從0.6 m/s增加到1.0 m/s時，車體的最大橫向加速度從0.817 m/s2增加到2.283 m/s2，相比增長179%。這是因為隨著冰速的增大，橋梁的橫向振動反應增加，進而通過車-橋耦合作用力傳遞給橋上行駛的車輛。另外，由2.2節分析可知，不同車速對于橋梁的橫向動力反應影響不大。可以預見，車速的變化對車體橫向振動影響輕微，故本節不再贅述。綜上所述，車輛的豎向振動反應受車速的影響較為明顯，隨車速的增加而增大；車輛的橫向振動反應隨冰速的增加而增大，受到了冰荷載的控制。

3 行車安全分析

3.1 車輛側滑評價指標

本文給出了橋上車輛行駛過程中的側滑評價指標，車輛某一車軸的側滑抗力FSR可以表示為

FSR=μFz,left+Fz,right-Fx,left+Fx,right

(17)

式中：Fz,left和Fz,right分別為某一車軸的左輪和右輪的豎向接觸力；Fx,left和Fx,right分別為某一車軸的左輪和右輪的橫向接觸力；μ為車輪與橋面的摩擦因數，本文選取摩擦因數μ= 0.6[22]。由式(17)可知，當車輛的側滑抗力接近0時，說明車輛接近于側滑狀態。

3.2 冰速的影響

當車輛以100 km/h的行駛速度通過橋梁時，3種不同冰速情況下車輛前軸和后軸的豎向接觸力，如圖12所示。由圖12可知，冰速的變化對車輛的豎向接觸力影響不大，這是由于冰速只會影響冰與橋梁結構的橫向相互作用力，而車輛的豎向振動主要是受到了橋面粗糙度的影響。因此，當車輛以同一速度在橋上行駛時車輛的豎向接觸力幾乎保持不變。當車輛以100 km/h的行駛速度通過橋梁時，3種不同冰速情況下車輛前軸和后軸的橫向接觸力，如圖13所示。由圖13可知，隨著冰速的增加，車輛前、后軸的橫向接觸力明顯增大，這說明快冰速增大了冰與橋梁結構的相互作用力，同時增大了橋梁傳遞給車輛的橫向接觸力。

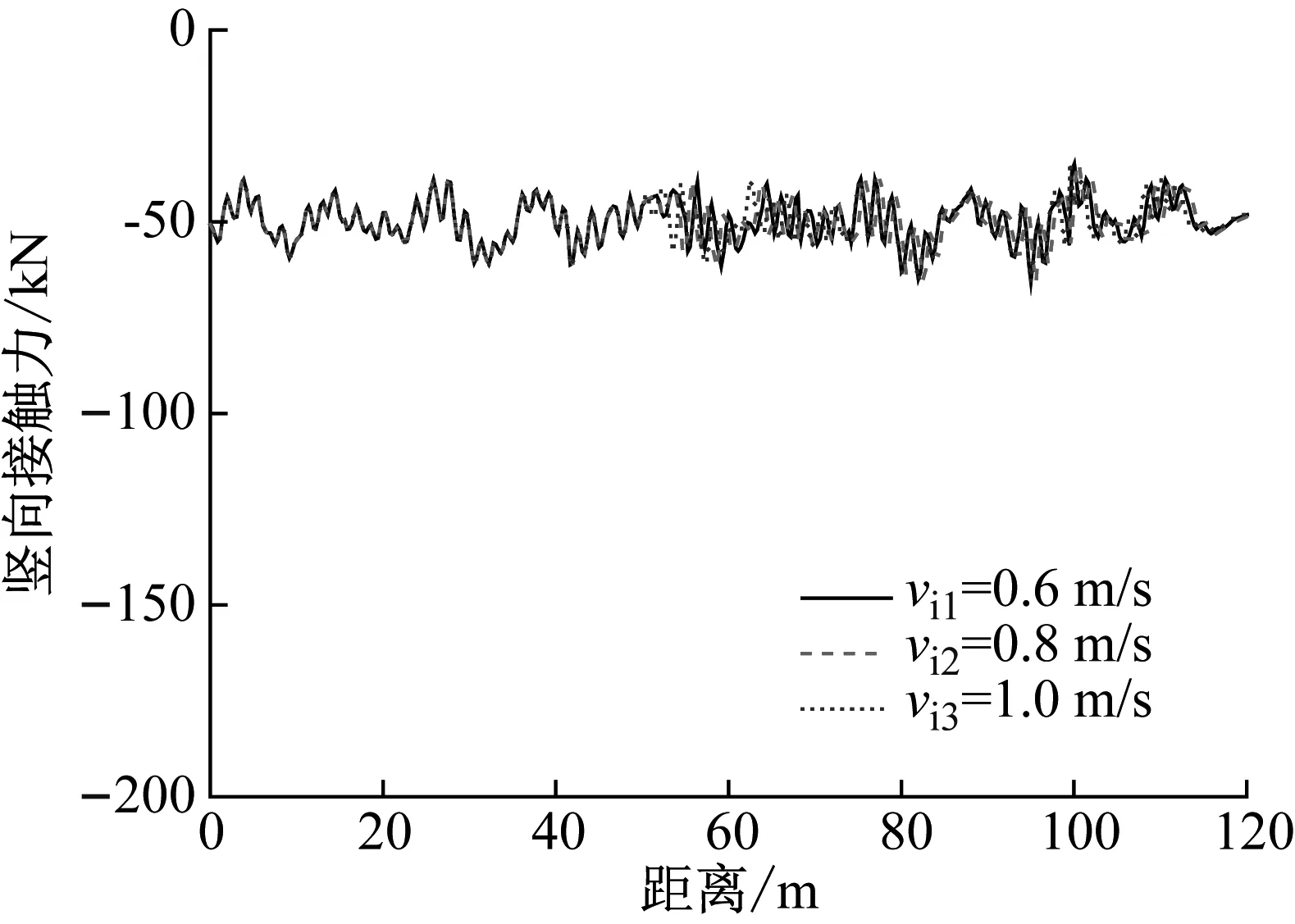
(a) 前軸豎向接觸力

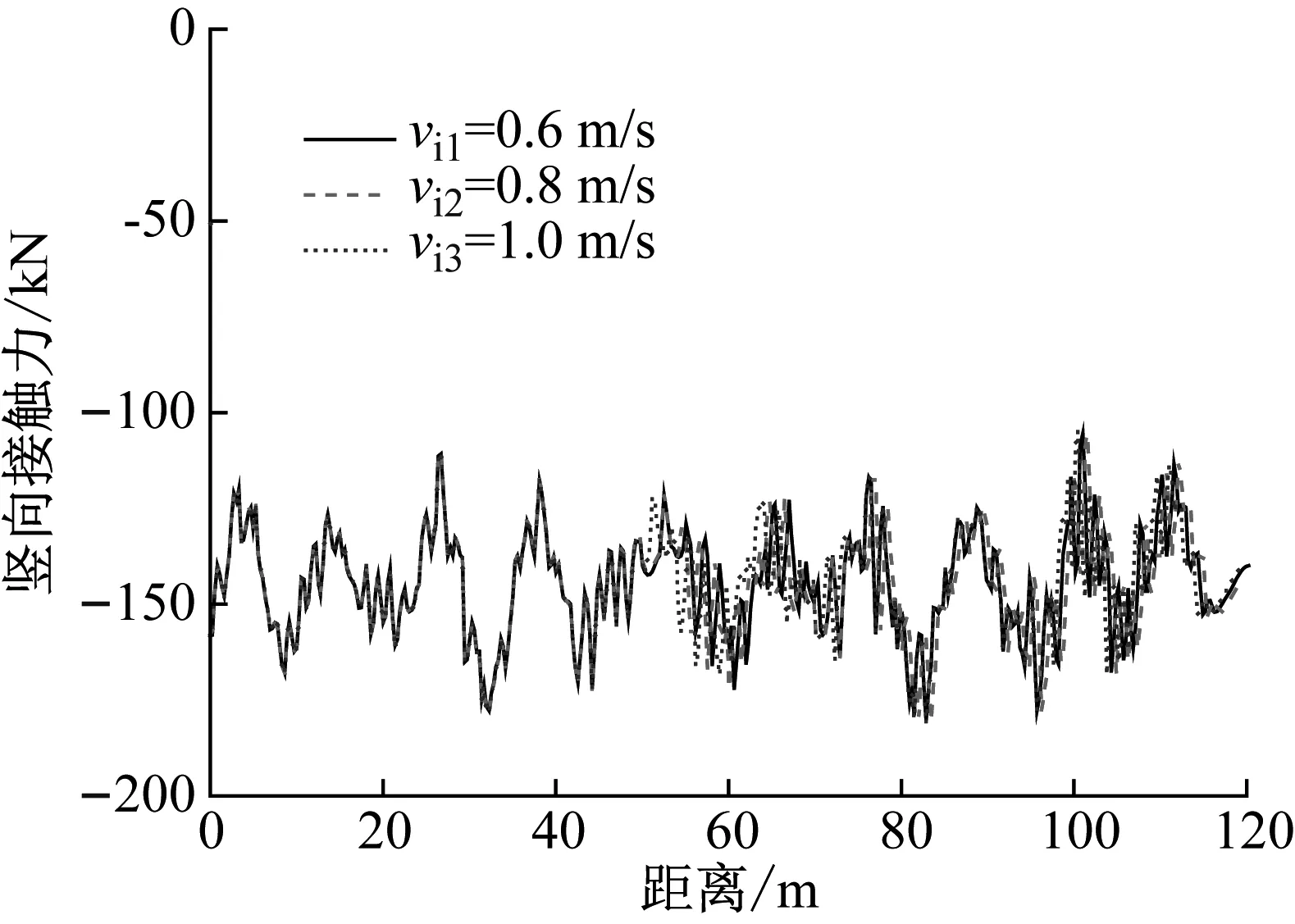
(b) 后軸豎向接觸力

當車輛以100 km/h的行駛速度通過橋梁時，3種不同冰速情況下車輛前軸和后軸的最小側滑抗力，如圖14所示。由圖14可知，隨著冰速的增大，車輛的最小側滑抗力明顯減小。當冰速為0.6 m/s和0.8 m/s時，前軸的最小側滑抗力為17.62 kN和15.16 kN。然而，當冰速為1.0 m/s時，前軸的最小側滑抗力僅為12.56 kN。結果表明，冰速的增大會降低抵抗側滑的安全儲備力，對橋上車輛的行駛安全不利。此外，車輛前軸車輪的最小側滑抗力要低于后軸車輪的最小側滑抗力。例如，在冰速為1.0 m/s時，前軸的最小側滑抗力為12.56 kN，后軸的最小側滑抗力為40.41 kN。這說明冰荷載作用下橋上車輛的前軸車輪比后軸車輪更容易發生側滑。

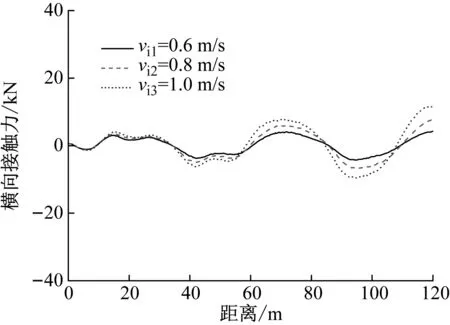
(a) 前軸橫向接觸力

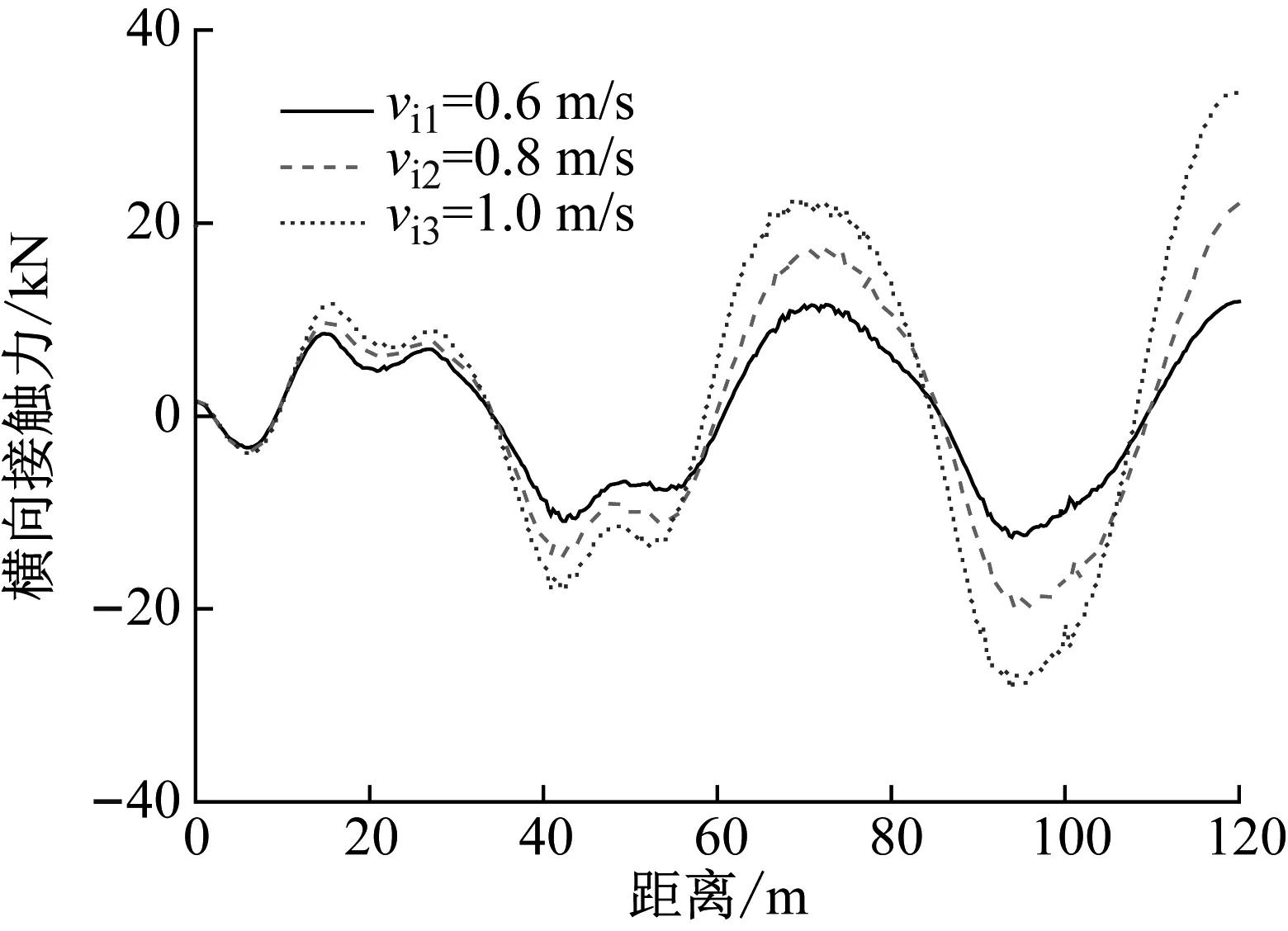
(b) 后軸橫向接觸力

3.3 車速的影響

當車輛以3種不同的行駛速度通過橋梁時，在冰速為1.0 m/s的情況下車輛前軸和后軸的豎向接觸力，如圖15所示。由圖15可知，隨著車速的增加，車輛前、后軸的豎向接觸力明顯增大，這說明了車輛在同樣的粗糙度橋面上行駛時，車速對車輛的豎向接觸力具有顯著影響。由圖15還可知，后軸的豎向接觸力遠大于前軸的豎向接觸力，這是由于車體重心位于整體車身的后部所導致的。

當車輛以3種不同的行駛速度通過橋梁時，在冰速為1.0 m/s的情況下車輛前軸和后軸的橫向接觸力和最小側滑抗力，分別如圖16、圖17所示。由圖16和17可知，無論前軸或后軸，車輛的橫向接觸力和最小側滑抗力均隨著車速的增大而減小。這是由于冰激橋梁結構自激振動會隨著冰與結構的相互作用時間的增加而增大，最終穩定在固定的振幅上。當車速較慢時車輛的過橋時間較長，增加了冰與橋梁結構相互作用的時長。因此，以較慢車速行駛的車輛會受到更大的振動反應，從而使得車輛的橫向接觸力增大，側滑抗力減小。例如，當車速為100 km/h和70 km/h時，前軸的最小側滑抗力為13.31 kN和11.56 kN。然而，當車速為40 km/h時，前軸的最小側滑抗力僅為8.84 kN。

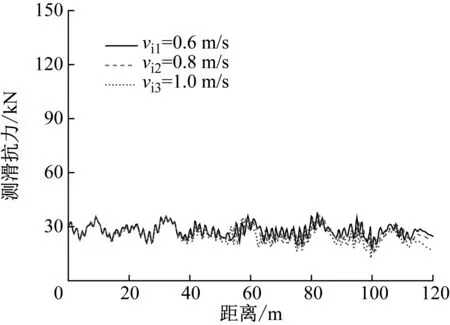
(a) 前軸最小側滑抗力

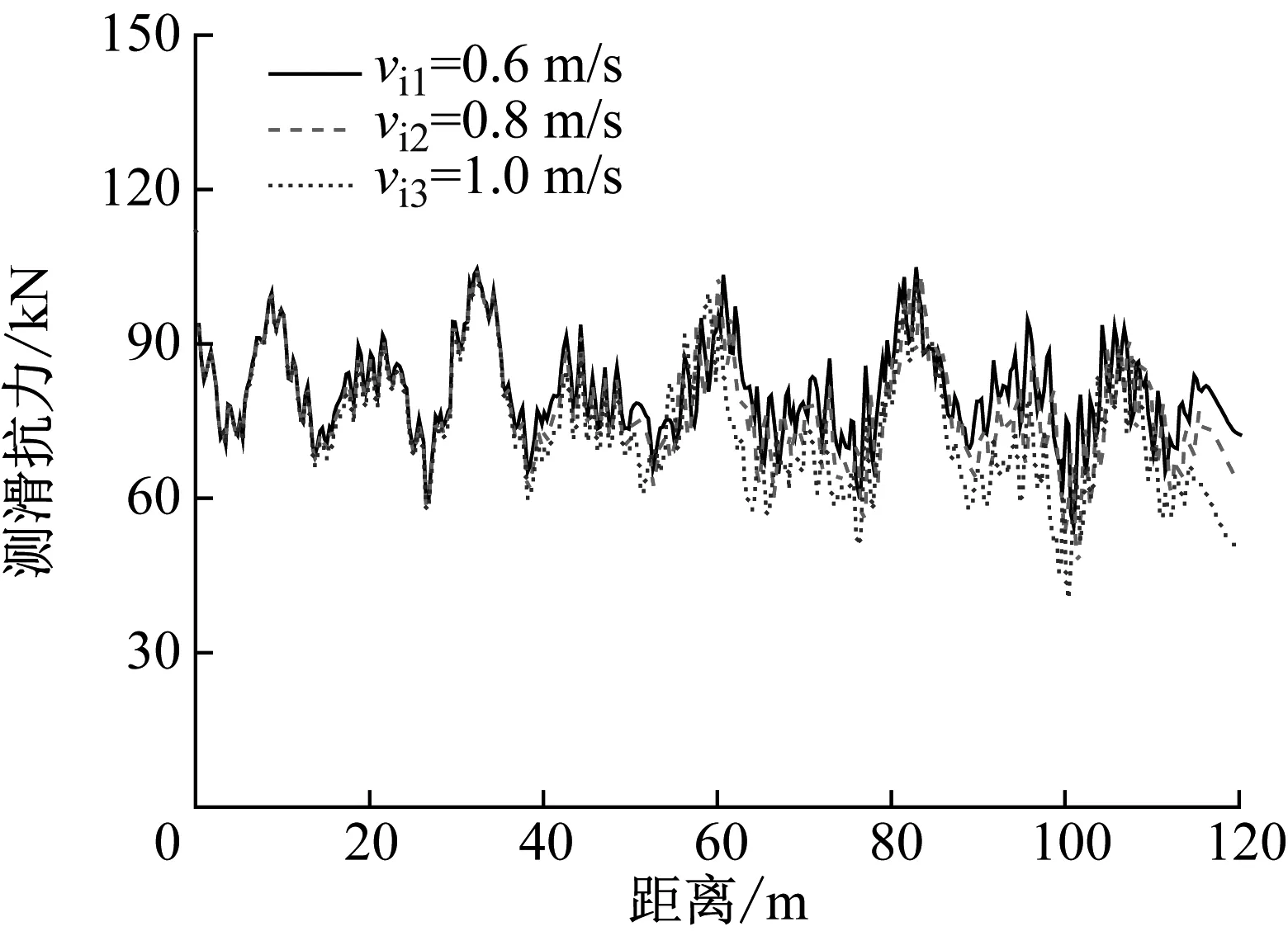
(b) 后軸最小側滑抗力

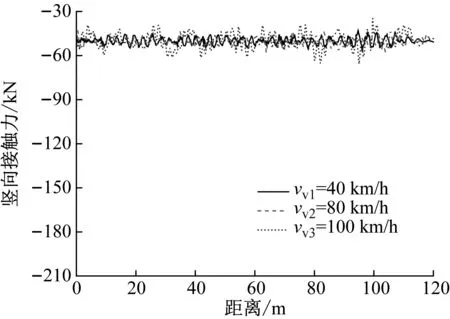
(a) 前軸豎向接觸力

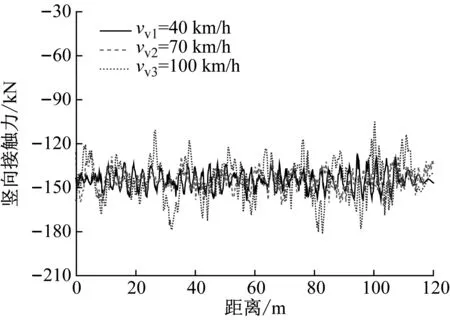
(b) 后軸豎向接觸力

由圖17還可知，車輛前軸的側滑抗力遠低于后軸的側滑抗力。例如，在車速為40 km/h時，前軸的最小側滑抗力為8.84 kN，后軸的最小側滑抗力為25.82 kN。此時，車輛的后軸車輪處在較為安全的狀態，然而車輛的前軸車輪非常接近側滑狀態，只有約為8 kN的安全儲備。

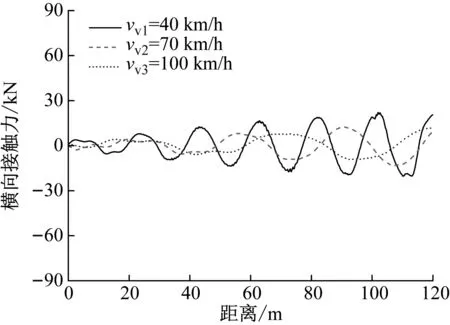
(a) 前軸橫向接觸力

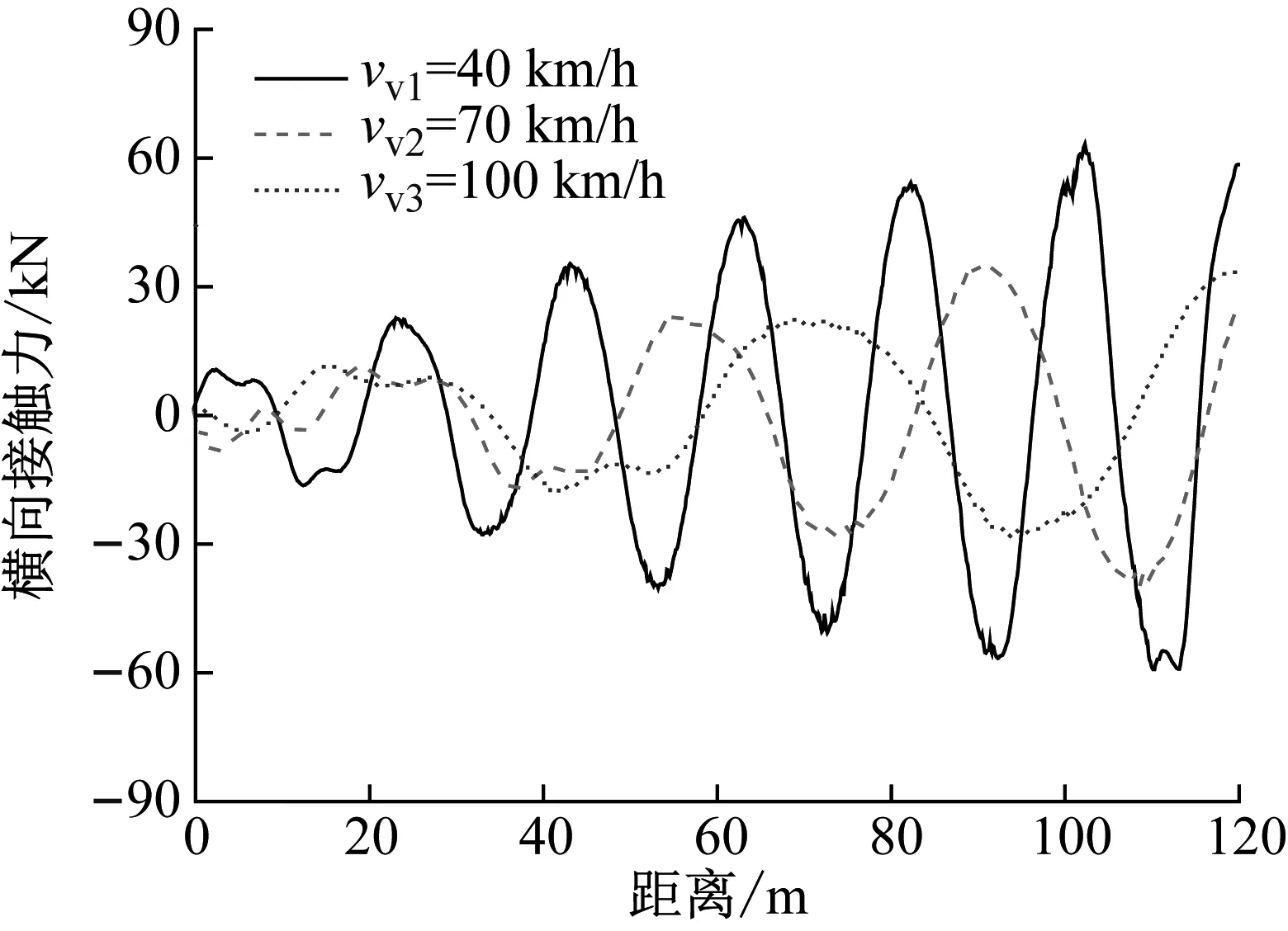
(b) 后軸橫向接觸力

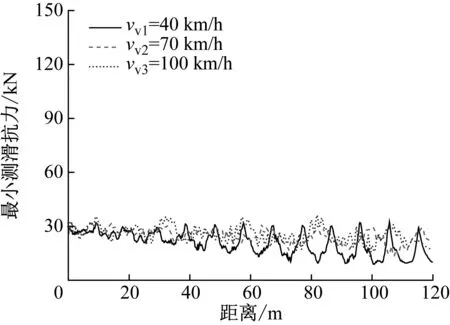
(a) 前軸最小側滑抗力

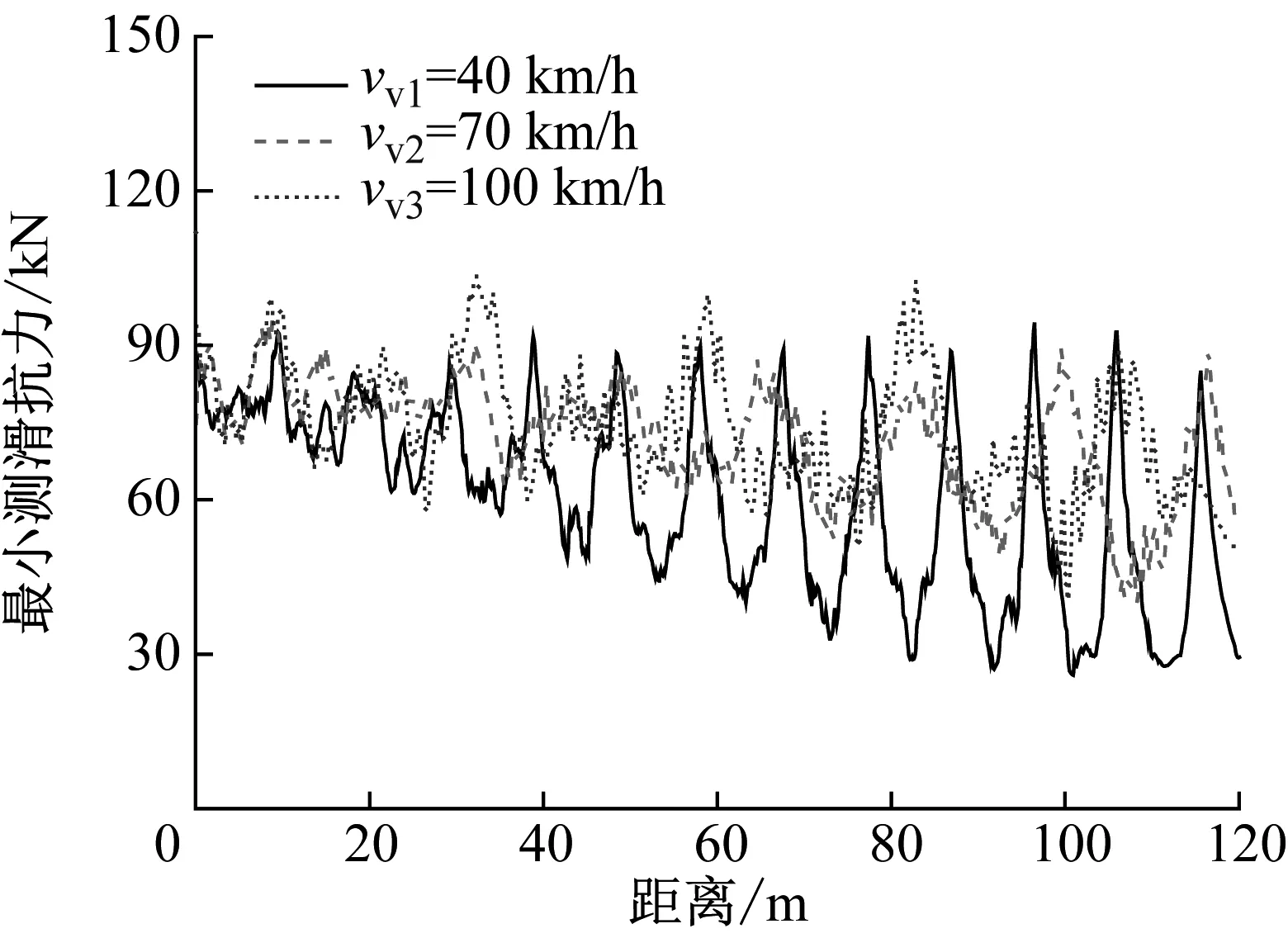
(b) 后軸最小側滑抗力

4 結 論

(1) 隨著車輛行駛速度的增加，橋梁和車輛的豎向動力反應均明顯增大。車輛行駛速度為100 km/h的橋梁最大豎向位移和車輛最大豎向加速度分別比40 km/h時增加了20%和125%；隨著冰速的增加，冰與車-橋系統的相互作用力增大，橋梁和車輛的橫向動力反應均明顯增大。當冰速從0.6 m/s增加到1.0 m/s時，橋梁的最大橫向位移和車輛的最大橫向加速度分別增加了102%和179%。這說明了車輛與橋梁的交互作用受到了車速和冰速的雙重影響。

(2) 當冰速從0.6 m/s增加到1.0 m/s時，車輛前、后軸的橫向接觸力均呈現增大趨勢，車輛前軸的最小側滑抗力從17.62 kN降低到12.56 kN。這說明快冰速會增大車輛的橫向接觸力，降低車輛的最小側滑抗力，不利于行車安全。此外，研究還發現橋上車輛的前軸車輪比后軸車輪更容易發生側滑。

(3) 車輛的橫向接觸力和最小側滑抗力均隨著車速的增大而減小。這是由于冰激橋梁自激振動會隨著冰與結構的相互作用時間的增加而增大，最終穩定在固定的振幅上。當車速較慢時車輛的過橋時間較長，增加了冰與橋梁結構相互作用時長。因此，以較慢車速行駛的車輛會受到更大的振動反應，從而使得車輛的橫向接觸力增大，側滑抗力減小，對行車安全不利。

(4) 本文所提出的車-橋-冰系統耦合分析框架可為冰荷載作用下跨海橋梁行車安全評估提供參考。