基于改進西原體模型的巖石流變特性分析

朱帥，李明飛，姜麗萍，竇益華，王智勇

1.陜西鐵路工程職業(yè)技術學院（陜西 渭南 714000）

2.西安石油大學 機械工程學院（陜西 西安 710065）

0 引言

巖石的流變包括蠕變、松弛和彈性后效，巖石的流變影響油氣井等巖石工程結構的穩(wěn)定性和安全性，因此，巖石流變特性的研究引起了人們的重視[1-2]。目前巖石流變研究的一般做法是：根據巖石流變的機理，建立描述巖石流變的模型和方程，實驗測量模型和方程中的關鍵參數，再將包含這些參數的模型和方程用于巖石流變分析[3-4]。

目前，不同工程領域的學者結合自身學科特點，有針對性地開展巖石流變特征研究。肖欣宏等人針對水環(huán)境下的軟巖工程安全問題，研究了低應力作用下的蠕變特性和該特性相同水壓條件下的瞬時應變，得出水壓高低和應力大小對蠕變特性的影響[5]。劉穎等人從工程施工及運行實際中發(fā)現不同含水狀態(tài)下的巖石蠕變特性問題，對砂巖工程試樣進行了蠕變力學試驗，對比干燥狀態(tài)下的砂巖變化得出其受含水量的影響情況[6]。貴州大學的王唯等人為了探索巖石全過程蠕變特性，改進傳統的Bingham模型，對比天然頁巖蠕變試驗結果，驗證其模型的適用性和可行性[7]。黃海軍對隧道圍巖在不同凍融循環(huán)次數下的蠕變特性進行試驗研究[8]。安徽理工大學的王游等為了克服傳統元件模型組合難以對巖石非線性蠕變特性具體描述的問題，改進廣義Kelvin 模型進行參數確定和驗證，為類似問題研究提供思路和借鑒[9]。很多學者通過改變流變元件組合，改進了巖石蠕變模型以驗證具體工程領域的巖石蠕變問題[10-11]。高子璐等人給改進模型的參數反演提供思路和方法[12]。國內外相關專家學者也采用大邊界地層條件仿真方法對巖石流變現象進行推演和性能研究[13-14]。復雜的工程背景下巖石的流變特性是復雜多變的，而西原體模型可較好地模擬巖石流變過程中的蠕變階段，這對研究流變地層巖石變化很有意義。

借鑒先進的研究經驗，以流變巖層與井筒的相互作用為工程背景，針對流變巖層與井筒相互作用時的力學行為變化問題，基于改進西原體模型的巖石蠕變，繼續(xù)探索巖石流變特性的后續(xù)松弛過程。

1 巖石流變本構關系及其改進

1.1 傳統西原體模型

巖石流變學理論主要研究巖石的應力-應變狀態(tài)及其隨時間增長的變化規(guī)律，建立恰當的本構模型顯得尤為重要。如圖1 所示，傳統巖石力學西原體模型包括胡克體，黏彈性體（凱爾文體），理想黏塑性體，能夠反映巖石的彈性、黏彈性、黏塑性[1]。

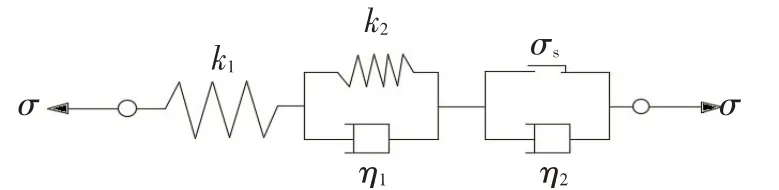
圖1 傳統的西原體力學模型

文章公式中涉及到的應力單位均為MPa，應變無量綱，時間以d計。圖1中，σ為模型應力；ε為應變；σs為巖石的屈服應力；k為彈簧的彈性系數；η為黏性元件的牛頓黏性系數；t為時間。其本構方程和蠕變方程如下[1]：

1）本構方程

當σ＜σs時，

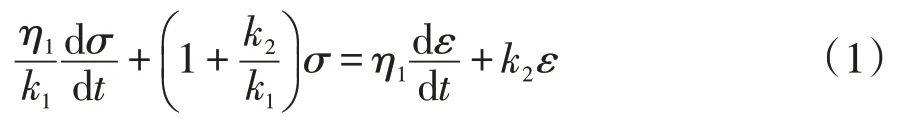
當σ≥σs時，

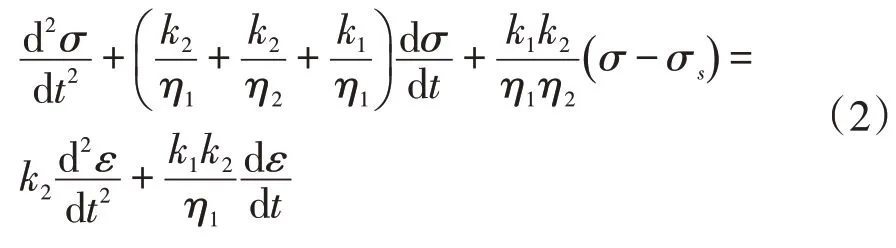
2）蠕變方程

當σ＜σs時，

當σ≥σs時，

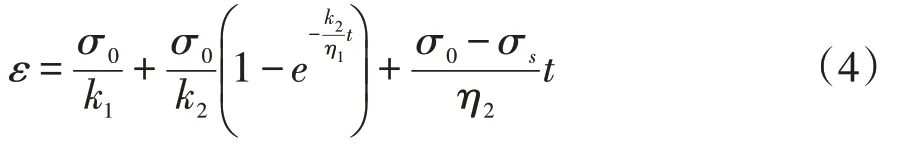
西原體模型可反映出當應力水平較低時，開始模型變形較快，一段時間后逐漸趨于穩(wěn)定，發(fā)生穩(wěn)定蠕變；當應力水平達到或超過材料某一臨界應力值后，漸漸轉化為不穩(wěn)定蠕變。因此，該模型在巖石流變特性研究應用中使用廣泛，特別在軟巖流變特性的描述中適用。傳統西原體模型的元件為理想的線性元件，只反映出蠕變的前兩個階段，不易完整描述巖石的其他流變特性。因此，為更全面地描述巖石的流變過程，在傳統西原體模型的基礎上，引入能夠表征巖石材料變形停止、應力隨時間增長而下降的參數[3]。為便于說明問題，以鹽膏巖地層中油氣井井筒應力變化為例進行研究。

1.2 改進后的流變模型本構關系

馬克斯威爾體模型是由彈簧和阻尼器串聯組合成的一種黏彈性體，該模型能對流變特征中的蠕變現象和松弛現象較好表達，符合鉆井初期井壁巖石的流變規(guī)律。為此，結合前人對西原模型的改進，將馬克斯威爾體與西原體模型結合起來，在模型的建立中串聯阻尼器，建立改進的巖石流變西原體模型，如圖2 所示。該模型阻尼器觸發(fā)條件是當模型應變達到某一應變值εA時，巖石進入加速蠕變階段對應的起始應變。

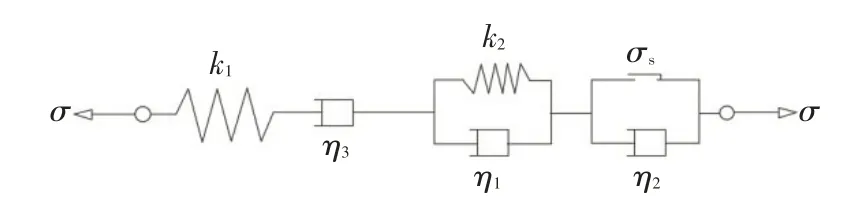
圖2 改進的西原體模型

圖2 中，σ為模型施加的總應力,MPa，σs為巖石的屈服應力，MPa；k為彈簧的彈性系數；η為黏性元件的牛頓黏性系數；ε為應變。依據文獻[3]，得到改進后的模型在加速蠕變階段的本構方程為[3]：

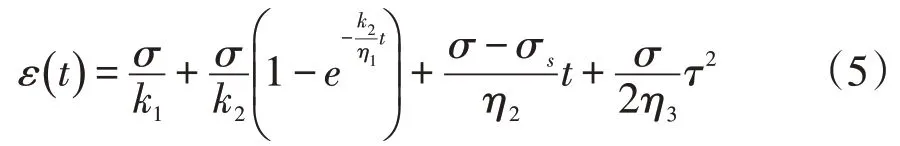
其中τ=t- |tε=εA,t｜ε=εA為巖石進入加速蠕變階段的時刻。

當t=0 時，施加應力σ0，并保持σ=σ0不變，得到該過程下的蠕變方程為：

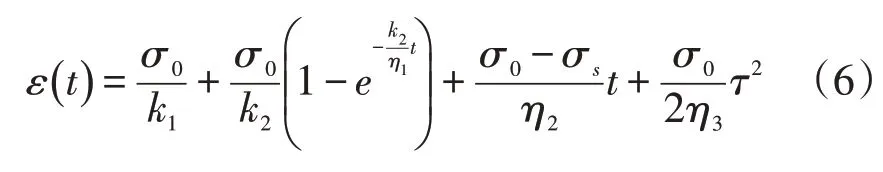
為了驗證改進西原體模型分析巖石流變的準確性，假設應力大于摩擦片屈服應力（σ＞σs），取彈簧元件的彈性系數k1、k2為10 MPa，牛頓黏性體的黏性系數η1、η2為10 MPa·d ，η3為50 MPa·d ，σ0為10 MPa，模型屈服應力分別取90、80、70、60和50 MPa，得到不同屈服壓力下改進西原體蠕變曲線，如圖3 所示。從蠕變曲線變化趨勢上看，巖石蠕變發(fā)生至第20 d時進入加速階段，直至第26 d蠕變加速結束。整體看，改進后的西原體模型完成了從蠕變減速到等速，再到加速的全過程，證明改進模型對蠕變過程描述的適用性，可進行后續(xù)流變特性的探索[15]。

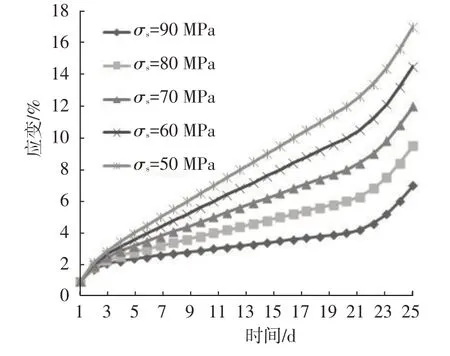
圖3 改進后的西原體模型蠕變曲線示意圖

1.3 改進后流變模型的松弛方程及其特征

當蠕變發(fā)生至一定程度時，巖石的變形將會保持在某一時刻的大小并且變化很小，此時認為應變ε為定值，此時，將模型的本構方程進行一階微分后得到：

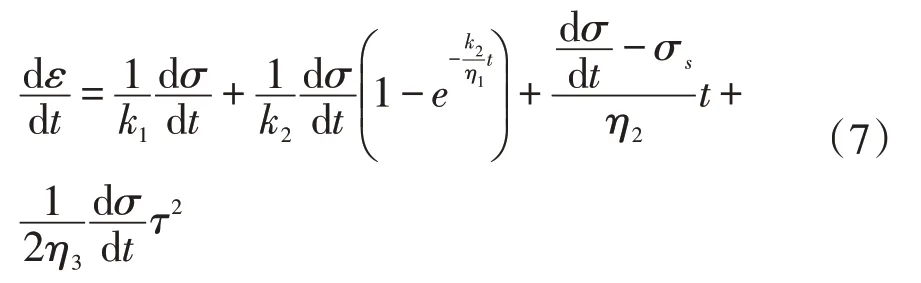
等式兩邊同時積分可得：

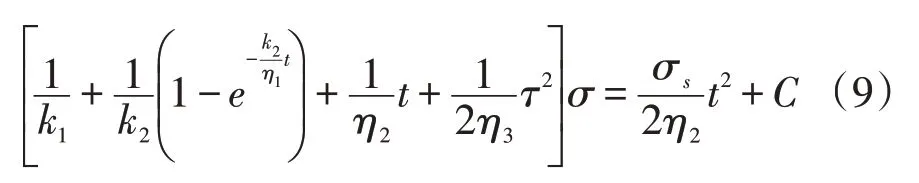
當t=0時，模型受到瞬時應力σ0，可得常數計算式：

得到的模型松弛方程表達為：

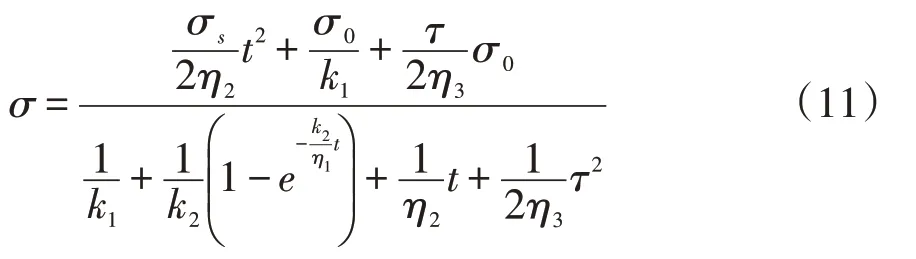
為了與巖石蠕變現象銜接，從蠕變過程結束后對松弛方程進行準確性驗證，保持模型相同賦值條件，對方程進行模擬。模型分別賦予50、60、70、80和90 MPa 等屈服應力值[15]。模擬出的松弛結果如圖4 所示，結合鉆井初期井壁巖石后續(xù)流變特性發(fā)展，對蠕變發(fā)生后一段時間內的松弛方程進行模擬，從蠕變全過程結束起認為變形停止，從曲線中應力隨時間的變化趨勢上看，模型受到的應力從27 d 開始逐漸減小，符合松弛現象發(fā)生的應力變化情況，說明該過程為巖石松弛階段。

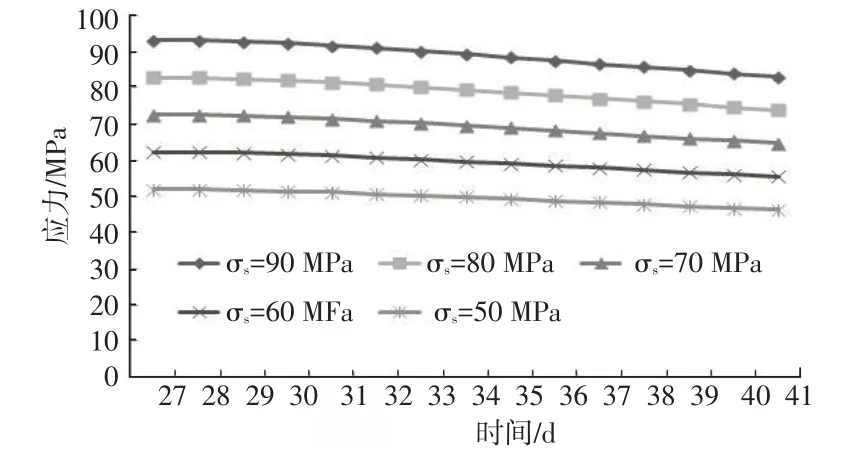
圖4 改進后的西原體模型松弛模擬結果

結合改進模型后的松弛方程和模擬松弛曲線結果分析看，方程中的巖石應力值在發(fā)生蠕變之后開始減小，松弛曲線中的應力隨時間的增長呈下降趨勢。結合鉆井初期井壁巖石的流變規(guī)律可以推斷，當巖石的應變值達到松弛發(fā)生條件時刻對應的應變值時，此后巖石流變特征就進入了松弛階段。在此之前，由圖3 可知模型處于蠕變階段的各個過程，在鉆井初期的流變地層中，由于該段地層巖石在鉆井后會發(fā)生應力變形，達到一定程度會貼合井壁，可以看成經歷了從蠕變開始到蠕變結束的過程，即受巖層自身地應力下的應變逐漸減小直至停止的過程。可以判斷流變地層巖石在蠕變之后產生松弛現象。為進一步驗證推斷，對松弛方程式（11）利用數學極限思想進行求解計算，過程如下。

隨著時間的推移，當t→∞時，松弛方程為“型”極限函數，隨即對方程進行求極限得：

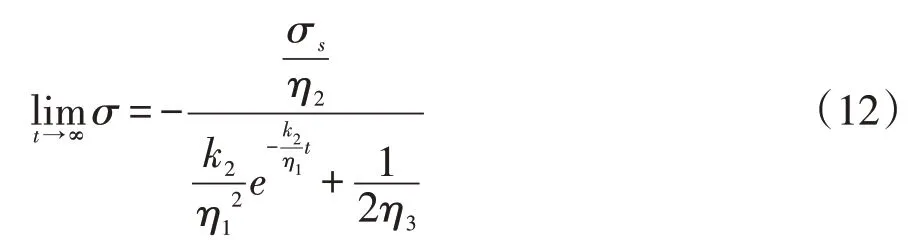
對于鉆井初期的井壁巖石流變的工程問題，鉆井導致的地層破壞，打破了流變地層原始地應力平衡，為平衡受力，應力則集中在井筒周圍，該狀態(tài)下的巖石就會發(fā)生蠕變現象。隨著蠕變全過程結束，地層與井筒緊密貼合，巖石停止蠕變變形，接著表現出應力隨時間的增長而減小的松弛現象，巖石流變特征會因實際工程條件的改變發(fā)生變化。

2 地應力計算及數值模擬

2.1 地應力計算驗證松弛方程

利用松弛方程進行應力計算時，存在黏性系數和彈性系數等5 個未知量，必須確定松弛方程中涉及到的這些系數。通常以實驗的方式對巖石流變本構關系中的方程進行參數識別，現有文獻對該方面的實驗研究較多，為方便計算，選用最貼近鉆井初期巖石流變特性的蠕變數據對松弛方程進行參數識別，取長山巖的蠕變數據作為計算條件，改進后得到的蠕變方程存在5 個參數[15]，相應取5 組數據，其中100、200、300、350 和400 h 時的應變值分別為0.051、0.054、0.058、0.063 和0.067 mm，初始應力為14.72 MPa，屈服應力為11.34 MPa，代入公式（11）可得到彈性系數和黏滯系數值分別為：

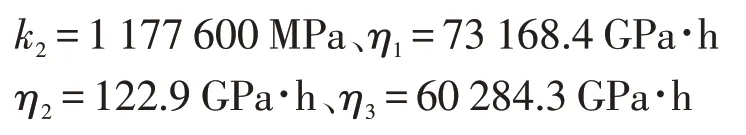
得到含具體參數的松弛方程：

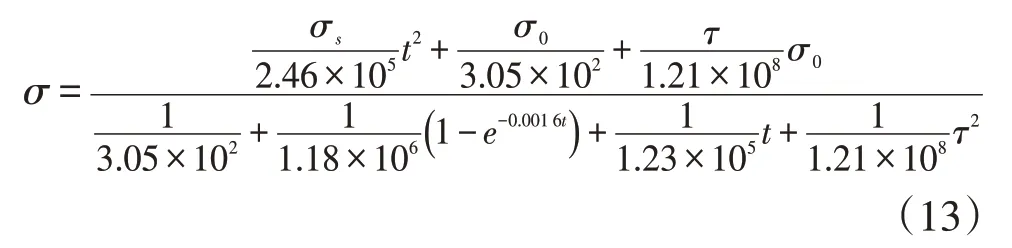
為了論證松弛方程結論的準確性，以某油田井區(qū)鹽膏巖地層中巖石力學參數為例，結合地應力理論公式和有限差分數值模擬兩種方法進行該地層地應力計算，結果與推導的流變松弛方程結果對比并分析誤差。根據某油田實際地質數據和測井資料可知，該井區(qū)東西埋深在3 522～4 468 m，南北埋深在3 768～4 428 m 的鹽膏巖蠕變地層，符合巖石流變特性的地層最大厚度約220 m，最小厚度約142 m，大部分厚度平均在142～168 m，符合條件的巖層包括泥巖夾層和泥膏巖夾層。該段地層巖石平均密度為2.186 g/cm3，屈服強度測算為65.4 MPa。其具體巖石力學參數見表1。

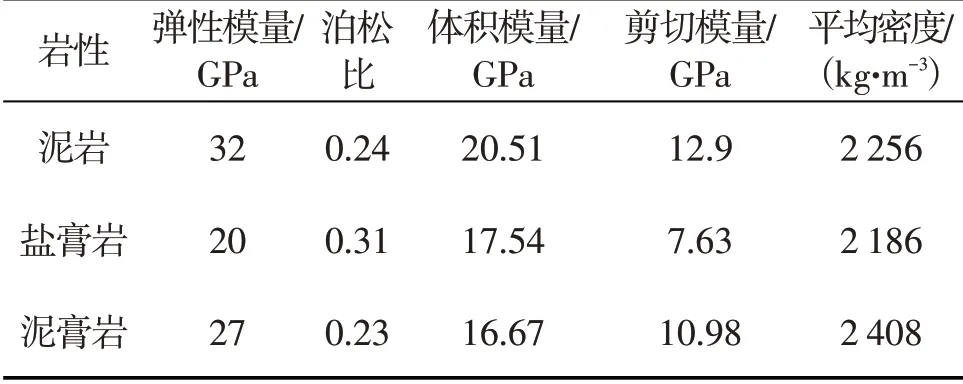
表1 某油田地層巖石力學參數

根據上覆巖層壓力計算公式計算地層初始地應力，可得所取地層垂直地應力為112.05 MPa。結合我國地理條件現狀，根據平均水平應力計算公式得116.4 MPa，水平主應力系數比值取0.7[1]，得到的水平最大主應力和水平最小主應力分別為136.94、95.86 MPa。

結合該地層巖石力學參數及理論計算的地應力結果，對含參數的松弛方程公式（13）進行賦值計算地應力。取屈服強度65.4 MPa，初始應力116.4 MPa，得到應力隨時間變化情況如圖5 所示，在26 h左右時應力值與理論計算結果大小相對應，水平應力平均值隨即呈現出下降趨勢，直至30.9 h時，平均應力值逐漸穩(wěn)定在113.08 MPa，與地應力理論計算結果對比，平均誤差為3.83%。

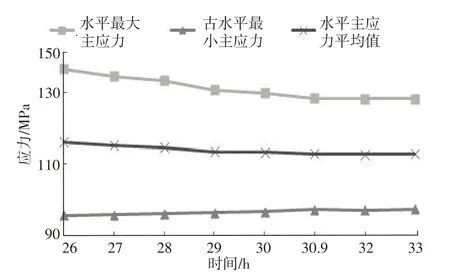
圖5 松弛方程應力隨時間的變化趨勢

2.2 數值模擬驗證松弛方程

為了多角度驗證流變松弛方程的準確性和可行性，再進行數值模擬計算。FLAC3D 有限差分軟件在大邊界模型下的數值計算較其他數值模擬軟件精度更高，計算更為準確，故選用該軟件對上述井區(qū)流變地層簡化進行建模計算。設定模型在水平方向上長度均為100 m，依據表1 中巖石力學參數，厚度方向自上而下按照20 m 泥巖層，30 m 鹽膏巖層、30 m 泥膏巖層進行劃分，模型總厚度為80 m。對整體模型統一劃分網格，單元格個數為1 000，共1 000個正方體網格單元。

選用軟件自帶流變模型中的cwipp鹽巖變形模型代替鹽膏巖層，彈性模量取20 GPa，泊松比取0.31，體積模量取17.54 GPa，剪切模量取7.63 GPa，地層中的重力加速度9.8 m/s2，與表1保持一致。設置模型上表面壓力為112.05 MPa，水平最大主應力為136.94 MPa，水平最小主應力為95.86 MPa。采用深埋工程初始地應力場的S-B 法計算生成，得到X方向上的水平應力云圖，如圖6所示[15]。

圖6的計算結果顯示，模型的x方向水平應力最大值為144.38 MPa；模型的y 方向水平應力最大值為99.62 MPa。利用FLAC3D 有限差分數值模擬結果對流變本構關系的計算結果進行校驗，水平方向應力平均誤差為7.25%。整體誤差較小，驗證了巖石流變本構松弛的準確性，可以用來計算流變地層的應力值。

圖6 初始地應力場x方向應力云圖

3 結論

1）改進的西原體模型適用于流變地層中的巖石變化規(guī)律。

2）在巖石發(fā)生蠕變之后，推導出的松弛方程體現出應力值隨著時間的增長而下降，說明巖石進入松弛階段。

3）將流變地層物理特征代入松弛方程進行計算，與地應力計算結果相比誤差為3.83%；與FLAC3D有限差分軟件數值模擬計算結果相比，平均誤差為7.25%，推導的松弛方程可計算流變地層的應力值。