指向數學建模素養的高考數學試題研究
——以2022年全國卷、新高考卷為例

葉德偉

(浙江大學教育學院 310028)

何羽茜

(浙江省杭州高級中學錢江校區 310021)

數學建模素養是對現實問題進行數學抽象，用數學語言表達問題、用數學方法構建模型解決問題的素養，是數學學科六大核心素養之一．數學建模過程既體現了數學與現實世界的相互作用，又離不開數學知識、方法、思想的運用．數學建模素養的發展必然會帶動其他數學學科核心素養的進步，而其他數學學科核心素養又是數學建模素養發展的重要基礎．因此，在教學實踐中提升學生的數學建模素養就顯得尤為重要．

《普通高中數學課程標準(2017年版)》(下簡稱《課標2017》)指出高考命題應注重對學生數學學科核心素養的考查，處理好數學學科核心素養與知識技能的關系，充分考慮對教學的積極引導作用．由此可見，數學高考試題是評價學生數學建模素養的重要載體之一，其對師生開展日常數學建模教學與評價提供了重要依據．因此，本文以2022年高考數學全國卷、新高考卷共計六份試卷為研究對象，分析高考試卷中指向數學建模素養的試題的分布、水平層次和命題特征，尋找數學建模與數學學科教學與評價的融合點，為開展數學建模教學、提升學生數學建模素養提供若干建議．

1 指向數學建模素養的試題在高考數學試卷中的分布

根據《課標2017》對數學建模素養的界定，我們將指向數學建模素養的試題界定為學生需要對現實問題進行數學抽象，經歷用數學語言表達問題、用數學方法構建模型才能解決的問題．初步對2022年高考數學全國卷、新高考卷進行分析，發現每份試卷都有試題指向學生數學建模素養的發展．進一步對這些試卷中指向數學建模素養的試題題型、背景、分值等信息進行統計，并根據鮑建生、葉立軍、姜浩哲等人的研究，將試題中所涉及的數學建模背景分為個人生活、社會生活、數學文化和科學研究四類，結果如表1所示．

根據表1可以看出，指向數學建模素養的試題總分在不同高考試卷中差距較大，其中最高的為全國甲卷(文科)29分，最低為新高考Ⅰ卷17分．從試題類型上看，指向數學建模素養的試題主要分布在選擇題與解答題中，少數分布在填空題中．從數學建模背景類型上看，涉及的數學建模背景以社會生活背景為主，以個人生活、科學研究、數學文化背景為輔，重視考查學生利用所學知識解決實際生活、社會生產問題的能力．

表1 2022年高考數學全國卷、新高考卷指向數學建模素養的試題相關信息

試卷位置數學建模背景背景類型分值總分全國甲卷文科選擇題第2題調查垃圾分類講座效果社會生活5分解答題第17題調查長途客車運行情況社會生活12分解答題第19題設計封閉包裝盒個人生活12分29分理科選擇題第2題調查垃圾分類講座效果社會生活5分選擇題第8題《夢溪筆談》“會圓術”數學文化5分解答題第19題比較學校體育比賽成績社會生活12分22分

續表

試卷位置數學建模背景背景類型分值總分全國乙卷文科選擇題第4題統計課外體育運動時長個人生活5分填空題第14題參加社區服務工作社會生活5分解答題第19題估計某種樹木總材積量社會生活12分22分理科選擇題第4題研究嫦娥二號繞日周期科學研究5分選擇題第10題計算象棋比賽獲勝概率個人生活5分填空題第13題參加社區服務工作社會生活5分解答題第19題估計某種樹木總材積量社會生活12分27分新高考Ⅰ卷選擇題第4題計算某水庫的蓄水量社會生活5分解答題第20題研究某種疾病與衛生習慣關系科學研究12分17分新高考Ⅱ卷選擇題第3題古建筑物剖面圖數學文化5分選擇題第5題文藝匯演排序社會生活5分解答題第19題調查某種疾病與年齡關系科學研究12分22分

2 數學建模素養在高考試題中的水平層次

要研究高考試題對數學建模素養的考查水平層次，就必須要依托一套科學的核心素養形成水平劃分標準．本文根據喻平提出的數學核心素養評價框架，結合《課標2017》對數學建模素養水平的界定，確定了如表2所示的數學建模素養水平編碼表．

表2 數學建模素養水平編碼表

水平編碼描述水平一:知識理解M1掌握高中階段常見數學模型的實際背景和數學描述;在熟悉的情境中,模仿學過的數學建模過程或根據已知模型解決問題;在交流過程中,能夠借助或引用已有數學建模結果說明問題水平二:知識遷移M2在熟悉情境中,發現問題并轉化為數學問題;在數學建模過程選擇合適的模型來解決常規性復雜問題;在交流過程中,能夠用模型思想說明問題水平三:知識創新M3在綜合情境中,運用數學思維進行分析,發現情境中的數學關系,提出數學問題;利用數學方法和語言創造性地建立合適的模型來解決非常規問題;在交流過程中,能夠用數學建模的結論和思想闡釋科學規律和社會現象

根據表2所建構的數學建模素養水平編碼表，對2022年高考數學全國卷、新高考卷中指向數學建模素養的試題進行編碼，統計各水平數學建模試題的數量.其中，此處的試題數量并非與題號一一對應，而是學生實際需要作答的任務量，例如，全國甲卷(理科)第19題共有2小題，則試題數量記為2．

編碼過程由兩位高中數學教師共同完成，兩人先依據數學建模素養水平編碼表獨立對2022年高考數學全國卷、新高考卷中指向數學建模素養的試題進行編碼，再經過多輪討論、協商并結合專家意見，最終得到各水平數學建模素養的編碼數據，具體如表3所示．

表3 2022年高考數學全國卷、新高考卷中各水平

數學建模試題數量

試卷M1M2M3全國甲卷文科320理科310全國乙卷文科311理科231新高考Ⅰ卷031新高考Ⅱ卷320總計14123

由表3可知，高考試卷中指向數學建模素養的試題對學生數學建模素養水平的考查以知識理解和知識遷移為主，主要考查學生在熟悉情境中 運用學過的數學模型解決問題或選擇合適的數學模型解決問題的能力；對知識創新水平的考查為輔，弱化對學生建構模型以解決非常規問題的要求．

3 指向數學建模素養的試題在高考試卷中的命題特征

3.1 以個人生活為媒介，解決身邊的數學問題，激發學習興趣

數學的應用已滲透到人們日常生活的各個方面．學生將個人生活中所遇到的現實問題轉化為數學問題，尋找合適的數學模型解決問題，體驗在實際生活中運用數學模型進行科學決策的過程，既能讓學生認識到數學與生活息息相關，激發學習數學的積極性，更能讓學生經歷用數學模型解決實際問題的過程，積累數學實踐的經驗．

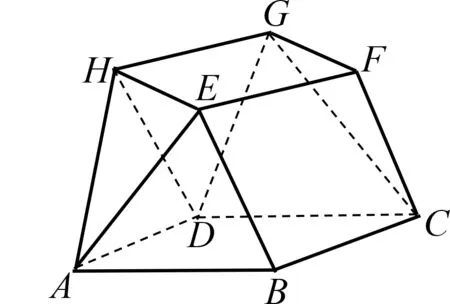
圖1

例1

(2022年數學全國甲卷(文科)第19題)小明同學參加綜合實踐活動，設計了一個封閉的包裝盒.包裝盒如圖1所示：底面

ABCD

是邊長為8(單位：cm)的正方形，△

EAB

,△

FBC

，△

GCD

，△

HDA

均為正三角形，且它們所在的平面都與平面

ABCD

垂直.(1)證明：

EF

∥平面

ABCD

；

3.1.3 保證柴油機冷卻及潤滑效果。要定期處理冷卻水腔中的污垢，保證柴油機濾清器的暢通運行，并且定期添加冷卻液及潤滑油。品質良好的冷卻油及潤滑液能夠有效減小氣缸套的磨損，延長柴油機的使用壽命。

(2)求該包裝盒的容積(不計包裝盒材料的 厚度).

評析 本題以綜合實踐活動中封閉的包裝盒設計為背景，第(1)小題需分析題中的幾何關系，分別取

AB

,

BC

中點為點

M

,

N

，根據面面垂直的性質定理得

EM

∥

FN

，再根據

AB

=

BC

、△

EAB

和△

FBC

為正三角形得

EM

=

FN

，從而判定四邊形

EMNF

為平行四邊形，得到

EF

∥

MN

，最后根據線面平行的判定定理可證得

EF

∥平面

ABCD

；第(2)小題需將該幾何體補形為長方體，可知包裝盒的容積為長方體體積減去四個全等三棱錐的體積，其中長方體底面積即為正方形

ABCD

的面積、高為△

EAB

的中線長可得長方體的體積三棱錐的底面是腰長為4 cm的等腰直角三角形、高即為長方體的高，可得一個三棱錐的體積則包裝盒的容積該題主要考查面面垂直的性質定理、線面平行的判定定理、補形法、棱錐體積公式等知識，在發展學生數學建模、直觀想象、數學運算、數學抽象、邏輯推理等素養的同時，讓學生利用數學知識解決個人生活中的真實問題，激發數學學習興趣．

3.2 以社會生活為素材，認識數學的社會功用，發展關鍵能力

數學作為一門被廣泛使用的學科，可以幫助人們在社會生產中搜集與處理信息、描述現象、探索規律，從而提高生產效率．高考數學試題通過真實的社會生活情境讓學生建立一些基于數學表達的經濟模型和社會模型，用模型的思想尋找生產中的最優解，既使學生認識到數學對社會價值創造、生產力發展的重要作用，又讓學生形成了解決社會生產問題的能力．

例2

(2022年數學新高考Ⅰ卷第4題)南水北調工程緩解了北方一些地區水資源短缺問題，其中一部分水蓄入某水庫.已知該水庫水位為海拔148.5 m時，相應水面的面積為140.0 km；水位為海拔157.5 m時，相應水面的面積為180.0 km，將該水庫在這兩個水位間的形狀看作一個棱臺，則該水庫水位從海拔148.5 m上升到157.5 m時，增加的水量約為

A.1.0×10mB.1.2×10m

C.1.4×10mD.1.6×10m

評析 本題以南水北調工程中某水庫的蓄水量計算為背景，學生需要將上升的水位高度轉化為棱臺的高

h

=

h

-

h

=157.5-148.5=9(m)，將水位為海拔157.5 m和海拔148.5 m時相應水面的面積轉化為棱臺的上下底面面積

S

和

S

，代入棱臺體積公式計算出水庫增加的水量約為

V

=1.4×10m．該題主要考查棱臺的體積公式，指向學生數學建模、數學運算、邏輯推理等素養的發展，并讓學生體會數學對提高社會生產效率的重要作用．

3.3 以數學文化為載體，重走數學發現之路，體現古人智慧

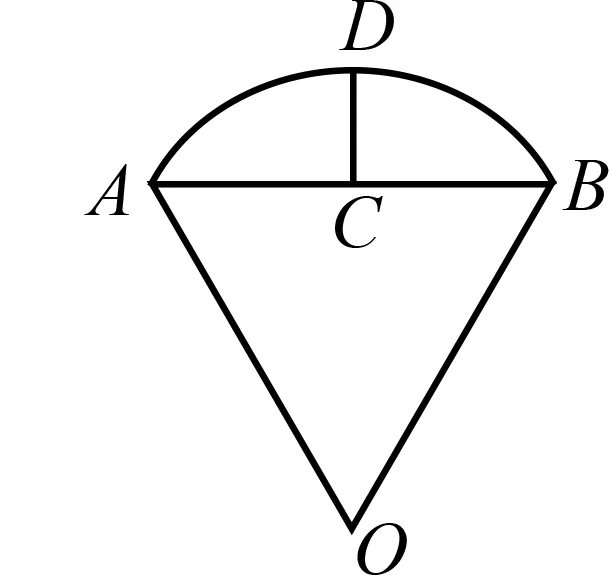
圖2

例3

(2022年數學全國甲卷(理科)第8題)沈括的《夢溪筆談》是中國古代科技史上的杰作，其中收錄了計算圓弧長度的“會圓術”.如圖是以

O

為圓心、

OA

為半徑的圓弧，

C

是

AB

的中點，

D

在上，

CD

⊥

AB.

“會圓術”給出弧長的近似值

s

的計算公式：當

OA

=2，∠

AOB

=60°時，

s

=( ).評析 本題以《夢溪筆談》中計算圓弧長度的“會圓術”為背景，需要學生理解“會圓術”給出的弧長計算公式，根據

OA

=

OB

=2和∠

AOB

=60°推導出△

AOB

為正三角形，故

AB

=2，連結

OC

得根據

C

是

AB

的中點、

CD

⊥

AB

，則延長

DC

可得

O

在

DC

上，由

D

在上知

OD

=2，故

CD

代入公式即得該題主要考查等邊三角形的性質、圓的性質、圓弧長度的計算，發展學生的數學建模、數學運算、數學抽象等素養，并讓學生體會中華優秀傳統文化的博大精深．

3.4 以科學研究為線索，實現學科深度融合，彰顯學科地位

數學是進行科學研究的重要基礎．數學理論的發展使得眾多科學問題得到解決，加快了人們認識自然、認識世界的進程．高考試題依托科學研究的背景，要求學生提取科學信息中的關鍵要素，建構數學模型以解決復雜科學問題、闡釋科學規律，顯化數學模型的科學含義，實現數學學科與科學學科的深度融合，不僅有效提升了學生的數學建模素養，更能使學生認識到數學的工具性和技術性價值．

例4

(2022年數學全國乙卷(理科)第4題)嫦娥二號衛星在完成探月任務后，繼續進行深空探測，成為我國第一顆環繞太陽飛行的人造行星，為研究嫦娥二號繞日周期與地球繞日周期的比值，用到數列依此類推，其中

α

∈

N

(

k

=1,2,…),則( ).A

.b

<

b

B

.b

<

b

C

.b

<

b

D

.b

<

b

評析 本題以研究嫦娥二號繞日周期與地球繞日周期的比值為背景，要求學生根據題目條件理解數列{

b

}中的

α

，根據作差法或不等式的性質比較數列各項的大小關系，通過排除法得到結論．該題主要考查數列各項大小的比較、數列的性質，發展學生的數學建模、數學運算、數學抽象、邏輯推理等素養，使學生體會數學對科學發展的重要作用．

4 提升學生數學建模素養的教學建議

4.1 加強整體設計，挖掘優質建模問題情境

研究發現，目前指向數學建模素養的試題在高考試卷中已占有一定比重(17～29分)，高考試題以個人生活、社會生活、科學研究、數學文化中的相關問題為背景，引導學生解決身邊的、社會中的復雜數學問題，探究科學研究、數學典籍中所蘊含的數學知識、方法和思想．日常教學中，教師應創設優質的數學建模情境，提升情境的真實水平，帶領學生發現其中的數學關系、提出數學問題，用數學的語言、符號建構數學模型以解決問題．具體來看，首先，優質的數學建模情境必須是真實且有意義的，例如以提高新冠肺炎檢測效率為問題情境開展分布列內容的教學；其次，數學建模問題情境必須是與學生認知起點、思維水平相匹配的挑戰性問題，例如引入放射性物質衰減的問題情境開展指數函數的教學；最后，優質的數學建模問題情境必須是學生感興趣的、能夠激發學生問題解決積極性的，例如以探究民間折紙藝術中對折次數與對折后總面積的關系為問題情境進行數列求和內容的教學．

4.2 探索融入方式，優化數學建模教學路徑

高考試卷中指向數學建模素養的試題的問題情境與學生的問題解決過程基本是緊密聯系的，例如，給出某一林區樹木根部橫截面積與材積量的數據，要求學生建立模型計算兩者的樣本相關系數．因此，教師應探索數學建模教學的合適路徑，提升學生的數學建模素養．具體看，有三種教學路徑：其一，在數學知識教學的過程中提升學生的數學建模素養，例如，在解三角形教學過程中，可引入測量旗桿高度的問題，要求學生運用解三角形的知識建立模型解決問題；其二，在數學方法教學的過程中提升學生的數學建模素養，例如可以引入推測未來人口數量的問題，要求學生運用歸納法建立模型解決問題；其三，在數學思想內化的過程中，可引入計算太陽系某行星運動軌道的問題，要求學生運用數形結合的思想建立模型解決問題．

4.3 開發課程資源，推動真實建模過程發生

指向數學建模素養的試題通過還原現實生活情境，如調查垃圾分類講座效果、統計課外體育運動時長，考查學生利用所學數學知識、方法和思想表達、解決生產生活中復雜問題的能力．為提升學生應對復雜問題的能力，教師應整合可用的課程資源，帶領學生走出課堂，挖掘生產生活現象背后的數學元素，在開展個人決策、社會調查、科學研究、數學典籍閱讀等活動的過程中學習數學，進一步認識數學對生產生活、科技進步、社會發展的作用，使學生具體化、情景化、體驗化、互動化地感知和參與數學學習，切實理解復雜問題、現象背后所蘊含的數學知識、方法和思想，推動真實數學建模過程的發生，從而提升數學建模素養．以“某市階梯電價的設計”項目為例，教師可要求學生設計問卷，隨機調查若干小區住戶的月用電量；接著，根據調查所獲得的數據查閱資料、訪談專家以探究階梯電價分檔、臨界值的設定原則和方法，建構某市階梯電價設定模型；最后，隨機選取居民開展調查，檢驗、闡釋所建構模型的科學性．學生在解決真實項目問題的過程中，學習相關數學知識，建立起解決復雜數學問題的思維框架，從而有效發展數學建模素養．

4.4 完善教學評價，促進數學建模素養落地

數學高考試題是開展數學教學評價的重要導向．研究發現，指向數學建模素養的高考試題對學生數學建模水平的評價已涉及知識理解、知識遷移和知識創新水平，學生需要努力理解試題中的真實情境，才能順利建立模型以解決問題．與之相適應的，教師應在日常教學過程中通過教學評價幫助學生理解真實問題情境及其背后所蘊含的數學知識、方法和思想，使數學建模試題中的真實問題情境成為學生解決日常數學問題的“必需品”而非“附屬品”，提升學生數學建模素養水平．具體看，可以根據數學建模教學內容、數學建模素養水平的劃分標準、高考數學建模試題的具體特點，以知識理解和知識遷移水平為主、知識創新水平為輔，按比例設計不同素養水平的數學建模習題，從而確保學生既不會因為理解難度過大而對數學建模試題產生畏懼心理，也不會因數學知識與真實情境結合膚淺生硬而失去解決真實問題、提升數學建模素養的機會．