挖掘素材價值 探索解題通法*

楊春霞

(江蘇省南京市第二十九中學初中部 210003)

諸士金

(江蘇省南京市橫梁初級中學 211515)

在解題教學中，部分教師只是教給學生具體的解法，而對問題的數學本質揭示得不夠全面.選取有價值的試題素材，有策略地進行解題教學，讓解題思路有跡可循，讓學生有法可依、學會解題通法，應是解題教學的價值訴求.筆者以在中考復習教學中遇到的一道2021年南京市中考填空壓軸題為例，進行有關解題教學的思考.

1 問題呈現與價值分析

圖1

(2021年南京中考第16題)如圖1，將

ABCD

繞點

A

逆時針旋轉到

AB

′

C

′

D

′的位置，使點

B

′落在

BC

上，

B

′

C

′與

CD

交于點

E.

若

AB

=3，

BC

=4，

BB

′=1，則

CE

的長為

.

本題以平行四邊形為基礎圖形，通過旋轉變換進行構圖，呈現形式簡潔優美，題小意長.試題立足幾何核心知識，綜合考查了平行四邊形的判定與性質、圖形運動的相關性質、相似三角形的判定與性質、全等三角形的判定與性質以及方程(組)思想等初中數學的主要知識點.考查內容較為全面，需要學生借助幾何直觀和空間想象感知平行四邊形在旋轉變換過程中的“變”與“不變”，厘清圖形局部元素中角、線段之間的關系，并能在較為復雜的模型中把握圖形整體之間的關聯，構建解決數學問題的有效模型，形成有條理、合乎邏輯的解題路徑.試題在解法上貫徹了求線段長度的通性通法，教師可以通過類似素材的解題教學，培養學生的數學思維和理性精神.

2 解法分析與通法探究

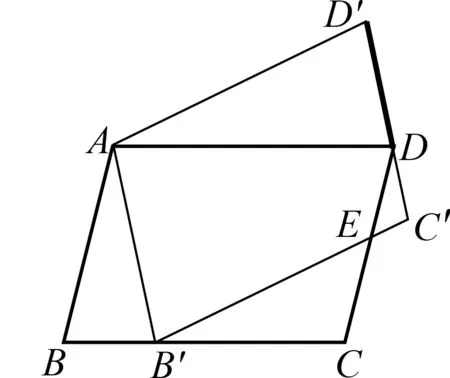
圖2

此題是一道填空題，題型雖小，難度卻不小.進行小題大做，深挖素材隱含的數學知識與解題方法，才能凸顯其教學價值.本題點

B

′落在

BC

上，則點

D

恰好落在

D

′

C

′上，看似巧合，實則必然.這點可以利用同一法簡要說明：如圖2，連結

DD

′，易證△

ABB

′∽△

ADD

′，故∠

B

=∠

AB

′

B

=∠

ADD

′=∠

AD

′

D.

又∠

B

=∠

AB

′

C

′,且∠

AB

′

C

′=∠

AD

′

C

′,所以∠

AD

′

C

′=∠

AD

′

D

,即點

D

在線段

D

′

C

′上.由點

B

和點

D

位置的特殊性，使得圖形整體關系豐富，能夠產生很多相似圖形.因此本題的構圖視野寬、解題路徑廣，宜為教學所用.下面從相似基本圖形的角度出發，進行解法分析與通法探究.

2.1 基于相似基本圖形“X型”構圖

在尋找或構造相似三角形模型時，常見的X型構圖求線段長是一個思考方向.本題首先可以線段

CE

所在三角形△

B

′

CE

為直接研究對象，嘗試尋找或構造與之成X型相似的基本圖形.

圖3 圖4

方法1

如圖3，根據旋轉可知

AB

=

AB

′，

AD

=

AD

′，∠

DAD

′=∠

BAB

′,所以△

ABB

′∽△

ADD

′,從而由

AB

=3，

AD

=4，

BB

′=1，得到易證△

DEC

′∽△

B

′

EC

，得到即解得

方法2

如圖4，過

C

′作

C

′

M

∥

BC

，交

DC

于點

M.

易證△

DMC

′∽△

ABB

′，則即解得因此由

C

′

M

∥

BC

可得△

B

′

CE

∽△

C

′

ME

，所以即解得

圖5

方法3

如圖5，延長

AD

，

B

′

C

′交于點

F.

易證△

ABB

′∽△

FAB

′，所以即解得

AF

=9．易證△

DEF

∽△

CEB

′，所以即解得

分析

本題由旋轉容易想到的是△

ABB

′與△

ADD

′相似，從而可得線段

DD

′和

DC

′的長度，后面很多方法都會用到

DD

′和

DC

′的長，不再贅述.方法1以

CE

為研究對象，從直觀上感知△

DEC

′與△

B

′

EC

呈X型相似，根據相似的性質，構建比例式進行求解.值得注意的是，這里的比例式其實隱含的是兩個關于

EC

和

EC

′的二元一次方程，對學生的代數推理能力和運算能力要求較高，很多學生會被這兩組比例式困住，難以得解.方法2和方法3均以

CE

所在的△

B

′

CE

為對象，分別過點

C

′和點

D

作輔助線，得到兩組相似.雖然需要構造相似，但計算難度比方法1要小，因此各有千秋.

2.2 基于相似基本圖形“A型”構圖

A型相似也是常見的相似基本圖形.本題構造A型圖可以把

CE

所在的三角形△

B

′

CE

，或

DE

所在的三角形△

DCE

作為研究對象，尋找或構造與之成A型相似的基本圖形.

方法4

如圖6，延長

BC

，

DC

′交于點

F

，過

F

作

FM

∥

CD

，交

B

′

C

′的延長線于點

M.

由

DF

=3，可得根據

FM

∥

CD

，可得△

B

′

EC

∽△

B

′

MF

，△

DEC

′∽△

FMC

′,所以即解得

圖6 圖7

方法5

如圖7，延長

BC

，

DC

′交于點

F

，過

C

作

CM

∥

B

′

C

′，交

DF

于點

M

．易證△

ABB

′∽△

CFM

，所以得到所以根據

EC

′∥

CM

，可得△

DEC

′∽△

DCM

，所以即解得

圖8

方法6

如圖8，過點

D

′作

D

′

F

∥

DC

，交

B

′

C

′ 于點

F.

易證△

D

′

FC

′≌△

B

′

EC

，所以

FC

′=

CE

，

D

′

F

=

B

′

E

=4-

C

′

E

．根據

D

′

F

∥

DC

，可得△

DC

′

E

∽△

D

′

C

′

F.

所以即解得

分析

方法4～方法6都是構造A型相似，但構造的思路不一樣.方法4直接以

CE

邊為研究對象，在△

B

′

EC

的外部，即

B

′

E

和

B

′

C

的延長線上構造，其中點

F

的確定是思維上的一個難點，需要結合圖形整體感知，選擇出這樣的一個特殊點.方法5則以與

CE

相關的線段

DE

為研究對象，在△

DEC

′的兩邊

DE

和

DC

′的延長線上過點

C

構造“A型”.與方法5不同之處在于，方法6是在△

DEC

′的另兩邊

C

′

E

和

C

′

D

的延長線上過點

D

′構造“A型”.

2.3 基于“一線三等角”模型構圖

審題時可以發現，∠

ABB

′=∠

AB

′

C

，且這兩個角的頂點在同一條直線上，由直觀感知和已有的構圖經驗，容易想到“一線三等角”模型.因此，可以嘗試從“一線三等角”的基本圖形出發，構造相似來求線段長.

方法7

如圖9，延長

BC

，

DC

′交于點

F.

由∠

ABB

′=∠

AB

′

C

′=∠

B

′

FC

′，易證△

ABB

′∽△

B

′

FC

′，得到即求得所以再由△

B

′

EC

∽△

DEC

′，得到即解得

圖9 圖10

方法8

如圖10，過點

C

作

CF

∥

D

′

C

′交

B

′

C

′于點

F

，則∠

ABB

′=∠

AB

′

C

′=∠

B

′

CF

，所以△

ABB

′∽△

B

′

CF

，得到即求得

CF

=1.因為

CF

∥

D

′

C

′，所以△

DEC

′∽△

CEF

，得到即解得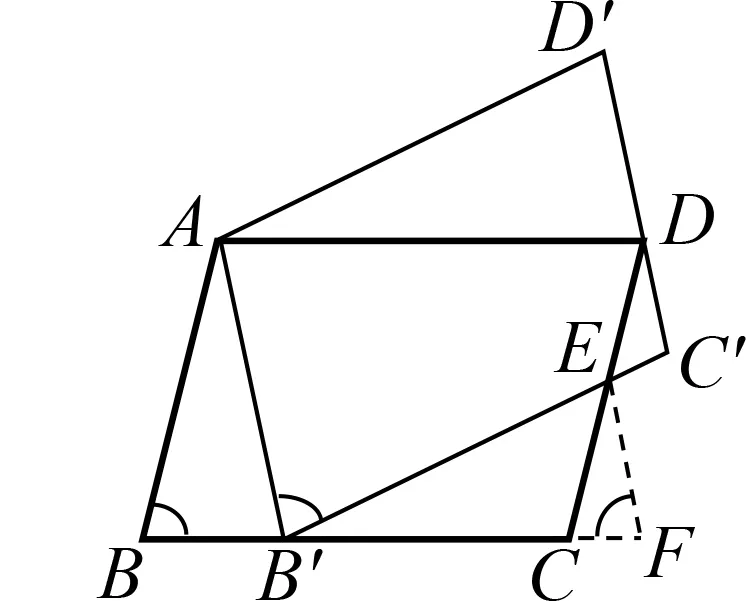

圖11

方法9

如圖11，過點

E

作

EF

∥

AB

′，交

B

′

C

的延長線于點

F

,則∠

ABB

′=∠

AB

′

C

′=∠

B

′

FE

，所以△

ABB

′∽△

B

′

FE

，得到即所以3+

CF

=3

EF.

易證△

ABB

′∽△

ECF

，所以可得

EF

=

EC

=3

CF

，解得

分析

方法7是從右下角向構造一線三等角模型靠攏，形成以

BC

為一線，∠

B

=∠

AB

′

C

′=∠

B

′

FC

′為三等角的模型，得到△

ABB

′與△

B

′

FC

′相似解決問題.方法8和方法9同樣是基于“一線三等角”模型，分別過點

C

和點

E

作平行來構造相似.

2.4 基于補全平行四邊形構相似

在構造“一線三等角”的過程中，“一線”托住了三個“等角”，這樣的直觀構圖感知在本題解法探究中還可以帶來不一樣的啟示，比如用“一線”托住凸出的角，將其補全為一個平行四邊形.

圖12

方法10

如圖12，過點

D

′作

MF

∥

AD

，交

BA

的延長線于點

F

，交

CD

的延長線于點

M

,則四邊形

FBCM

為平行四邊形，所以

FM

=

AD

=4，

FA

=

MD.

易證△

ABB

′∽△

DMD

′，所以即解得所以再證△

B

′

CE

∽△

D

′

FA

，所以即解得

圖13

分析

方法10在點

D

′處作平行補全了平行四邊形，往一線三等角模型方向去靠攏，但在靠攏中卻發現，此處并不是一線三等角，而是一線二等角，柳暗花明又一村，∠

M

=∠

ADD

′為證明三角形相似提供了新的思路.類似地，也可以在點

B

、點

C

及點

C

′處補全平行四邊形，構造圖13～ 圖15進行解決.這四種方法均是通過構造平行四邊形，形成一線二等角的模型，然后再尋找三角形相似，建立線段比例關系求得

CE

長.

圖14 圖15

2.5 基于平移轉化構相似

在方法1的分析中，我們知道△

ABB

′∽△

ADD

′是比較容易發現的，而要求線段

CE

的長，思考

CE

所在△

B

′

CE

與△

ADD

′的關系也是聯想的一個自然方向.因此，能否在△

ADD

′內尋找或構造與△

B

′

CE

相似的圖形呢？這里借助圖形變化中的平移縮放就可以得到如下的方法.

方法11

如圖16，延長

CD

，

AD

′交于點

F

，由△

ABB

′∽△

ADD

′，得再證△

ADF

∽△

B

′

CE

和△

DD

′

F

∽△

DC

′

E

，分別得到和即解得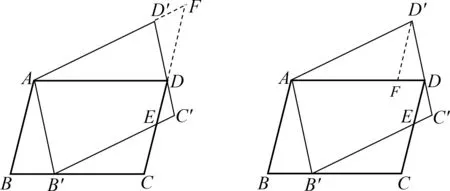

圖16 圖17

方法12

如圖17，過

D

′作

D

′

F

∥

AB

，交

AD

于點

F.

由△

ABB

′∽△

ADD

′,得易證△

ABB

′∽△

D

′

FD

,得到即解得所以易證△

AD

′

F

∽△

B

′

EC

,得到即解得

分析

方法11與12的解題思路類似，均源于通過平移縮放構造與△

B

′

CE

相似的直觀感知.在幾何解題中，與相似的幾種常見基本圖形一樣，平移縮放也是相似構圖的一個重要切入點.方法11、12都是將△

B

′

CE

往上平移縮放與△

ADD

′進行相似構圖，不同的是，一個是以

AD

為對應邊構圖，另一個是以

AD

′為對應邊構圖.

3 解題啟示與教學建議

在解題教學中，既要讓學生知其然，更要讓學生知其所以然，注重解題思路的探尋過程，積累思維活動經驗.引導學生經歷怎樣審題、怎樣想到思路方法、為什么要這樣想、還可以怎樣想的過程，通過對一道題目的講解，達到做一題通一類的效果，這是解題教學的價值所在.本題解法豐富，從其中任何一種相似的基本模型出發，都能自然產生解題路徑.而解法的自然生成，需要我們在平時的幾何解題教學中注重培養學生的發散聯想、模型意識和結構化思想，讓學生想得到、想得通、想得妙！

3.1 關注發散聯想，弄清怎么想

怎么做固然重要，怎么想更為重要.波利亞告訴我們，解題離不開最近聯想，從條件出發，從問題出發，從知識點出發，從數學基本模型出發，都是可以進行聯想的方向.教學中要多鼓勵并指導學生學會從上述方向發散思維，進行聯想.比如，由本題已知條件出發進行最近聯想，你可以初步得到哪些結論？整合條件和問題進行進一步聯想，要求線段

CE

的長需要做什么？再比如，從旋轉這一知識點出發，你可以得到什么？從基本模型出發，本題圖形中你又發現了哪些常見的基本圖形？由此獲得更多的需知對象.數學是思維的體操，解題教學中要引導學生進行最近聯想，學會用數學的方式發散思維，提高數學思維能力，積累解題活動經驗.

3.2 關注數學模型，聚焦怎么做

在本題的解法探索過程中可以發現，解題路徑的自然生成離不開數學的基本模型.本題幾乎覆蓋了相似圖形中所有常見的基本圖形，一是基于相似基本模型，往熟悉的基本圖形X型、A型構造相似；二是基于相似的經典模型，往“一線三等角”構造相似；三是基于空間想象，借助補全平行四邊形構造相似；四是基于幾何直觀，借助圖形平移變換構造相似.從每一種相似基本圖形出發均可找到解題方向，成功抵達，從而形成多樣的解法.因此，在平時的教學中，教師應強化學生的數學建模意識，一方面要共同歸納常見的幾何模型，深刻理解模型的關鍵特征；另一方面要引導學生有意識地從復雜的圖形中分解出或補全為常見的基本圖形，從而把陌生的、復雜的問題轉化為熟悉的、簡單的問題，提高學生的模型意識和利用模型解決問題的能力.

3.3 關注知識結構，重視回頭看

數學的解題研究看似解決一個問題，實則要教給學生思考問題的方式，由一個問題打通知識間的內在關聯，將碎片化的知識結構化，形成解決問題的通性通法，從而解決更多問題.本題目標是求線段

CE

的長度；對于線段求長問題，在整個初中階段有很多方法，如利用線段和差、倍數等數量關系求長，利用勾股定理三邊關系求長，利用全等三角形的相等關系求長，利用相似三角形的比例關系求長，利用三角函數邊角關系求長等，這些方法串聯起來就形成了一個線段求長的知識鏈條，也就是線段求長的通法.而本題利用相似求線段

CE

的長度即是這個知識鏈條中的一個知識節點.解題教學中，要引導學生梳理這樣的知識與方法鏈條，從而形成知識結構網.對于解決問題的通性通法，需要引導學生不斷地總結和回顧反思，才能讓學生在遇到新的問題時有法可想、有路可走，進而培養學生的數學高階思維，形成自主探究問題的解題經驗.

波利亞曾說：“如果你希望從自己的努力中取得最大的收獲，就要從已經解決了的問題中找出那些對處理將來的問題可能有用的特征.”本題已經塵埃落定，但其解法的探究給幾何解題的教與學帶來了很多啟示.解題即是縮小差距，縮小差距就是使已知與未知互相靠攏，我們在追求縮小差距的抵達，我們更是在享受一場互相靠攏的旅程，最終實現那美妙的雙向奔赴.