斯坦納-萊莫定理的λ-推廣
孫四周
(江蘇省蘇州市吳江盛澤中學(xué) 215228)
初等幾何中有個名氣非常響的定理——斯坦納-萊莫(Steiner-Lehmer)定理[1],內(nèi)容如下:
如果一個三角形的兩條內(nèi)角平分線相等,則該三角形是等腰三角形.
歐幾里得將該結(jié)論作為定理收入了《幾何原本》,對于其證明卻只字未提.直到1840年經(jīng)萊莫(C.L.Lehmus)重新提起,斯坦納(J.Steiner)首先給出了證明,引起了數(shù)學(xué)界極大反響,從此而被稱為“斯坦納-萊莫定理”.此后百余年,全世界的各種雜志上經(jīng)常可以看到論證這個定理的文章,至今已有接近百種證明.1980年,美國《數(shù)學(xué)教師》月刊還登載了這個定理的研究現(xiàn)狀.這個定理能夠保持如此持久的熱度,主要是因為它符合“著名定理”的特征,比如:表述非常簡單,結(jié)論看似顯然而證明卻往往涉及更深刻的內(nèi)容.
有趣的是,2012年文[2]用中國古人所擅長的“割補求積法”在不添加任何輔助線的情況下,給出一個簡潔(也可以說是“中國化”)的證明.并引申出13個定理,拓寬了它的應(yīng)用.本文將向另一個方向出發(fā),首先把“角平分線”換成“三等分角線”,進而給出任意等分角的推廣(本文中單字母表示角時意義如下:A=∠BAC,B=∠ABC,C=∠BCA).
1 三等分角的Steiner-Lehmer定理

圖1

證明由S△ABD+S△ACD=S△BAE+S△BCE知,


如果A>B,則①式左邊為正,右邊為負;如果A 類似地,對于三等分角的另外一條分角線,Steiner-Lehmer定理也成立.即 證明同上,略. 如果改成“四等分角”“五等分角”……“n等分角”,是否還成立呢?經(jīng)研究發(fā)現(xiàn),結(jié)論是肯定的.事實上我們有更一般的推廣. 圖2 定理3△ABC中,D,E分別是邊CB,CA上的點,且∠BAD=λA,∠ABE=λB,其中λ是常數(shù)且λ∈(0,1),則AD=BE的充要條件是CA=CB. 此定理的證明比較繁瑣,為了體現(xiàn)其層次性和關(guān)鍵技巧,我們先證下面的兩個引理,再將證明逐漸展開. 引理1若λ∈(0,1),A,B是△ABC的內(nèi)角,則A>B的充要條件是sinλA>sinλB. 證明只要證明當(dāng)x∈(0,π)時,f′(x)>0恒成立即可. 記g(x)=sinλx-λsinx,則g′(x)=λcosλx-λcosx=λ(cosλx-cosx),因為0<λx 由引理1,2知,若A>B,則上式左邊為正,右邊為負,矛盾;若A 圖3 在定理3中,研究線段AD與BE的交點S(圖3),以及由此產(chǎn)生的線段SA和SB,也是一個很有意義的課題,并且可以得到一系列有價值的結(jié)果. 定理4△ABC中,D,E分別是邊CB,CA上的點,且∠BAD=λA,∠ABE=λB,其中λ是常數(shù)且λ∈(0,1),AD,BE的交點是S,則SA=SB的充要條件是AD=BE. 證明一方面,在△ABS中,SA=SB?λA=λB?A=B.另一方面,△ABC中,AD=BE?A=B(定理3).綜合即知SA=SB?AD=BE.證畢. 綜合定理2和定理4,立刻知: 定理5△ABC中,D,E分別是邊CB,CA上的點,且∠BAD=λA,∠ABE=λB,其中λ是常數(shù)且λ∈(0,1),AD,BE的交點是S,則SA=SB的充要條件是CA=CB. (1)鉆孔放樣。在確定帷幕灌漿軸線的過程中,嚴(yán)格按施工圖紙進行測量放樣。應(yīng)用木樁對孔的位置進行標(biāo)識,合理控制樁距,相鄰樁距之間的距離控制在20m,在正式開鉆前,為了保證孔位和設(shè)計位置之間的距離≤50mm,應(yīng)用米尺再次進行復(fù)核。 定理6△ABC的內(nèi)角平分線AD,BE的交點是S,若SA=SB,則CA=CB(圖3). 按照定理6的構(gòu)圖原則,我們構(gòu)造更具一般意義的圖形,可得: 圖4 根據(jù)歐幾里得第五公設(shè)知,射線AC′與BC′的交點C′在C的同側(cè). (1)如果0<λ<1,則C′在△ABC的內(nèi)部,即為定理5,已證; (2)如果λ=1,則C′與C重合,顯然;
2 Steiner-Lehmer定理的λ-推廣

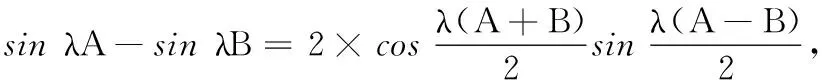




3 Steiner-Lehmer定理的等價形式