變高程水位面初始有效應力場生成方式探討

宗學才，侯付闖

(1.東營市水務局，山東 東營 257091；2.陜西中凱恒瑞工程項目管理有限公司，西安 710000)

1 概 述

隨著城市建設步伐的加快，大量工程不斷興建，其中有大量的隧道工程位于水下或一部分位于水上、一部分位于水下，形成水下建筑。在采用FLAC3D軟件對隧道圍巖進行受力分析時，勢必遇到位于水下和部分位于水下的建筑的初始應力場生成問題，多數學者在應用FLAC3D軟件進行有關隧道圍巖的模擬時，并未明確說明涉及水的條件下初始應力場是如何生成的[1-5]。華福才[6]基于MATLAB軟件和FLAC3D有限差分軟件對青島地鐵施工中涉及水頭、圍巖滲透特性等相關關系進行了研究。孫闖等[7]對上海市盾構法施工的某越江隧道進行了模擬，主要研究了盾構掘進過程中管壁后注漿壓力與土體變形之間的關系。崔鐵軍等[8]采用FLAC3D軟件對盾構隧道的施工過程進行了模擬，主要研究了所構建模型的特點與計算效率和最終結果的關系。李林毅等[9]通過采用FLAC3D軟件分析了隧道斜井工程單層襯砌的受力特點，并將計算結果和復合襯砌的受力特點進行比較，研究結果為現場災害防治提供了依據。馬春景等[10]采用FLAC3D軟件對富水區地鐵隧道土壓平衡盾構施工的水力耦合進行了模擬，結果顯示所開發方法對水力耦合計算的有效性。

本文基于砂柱試驗在FLAC3D中構建模型，通過變高程水位面設置，分析研究建筑位于水位面以下和部分位于水位面以下的情況下，初始應力場生成方法，研究結果可為涉及地下水位條件下，應用FLAC3D進行相關問題研究時初始應力場的設置提供依據和指導。

2 FLAC3D計算準備

在準備采用FLAC3D進行變高程水位面砂柱模型試驗時，需要事先生成正確的初始應力場。由于涉及地下水，初始應力場的生成相對于無地下水時更為復雜。FLAC3D為摩爾庫倫彈塑性本構模型材料涉及有水條件下初始應力場的生成提供了兩種方法：

1) 在設置了正確的孔隙壓力分布時，將處于地下水位面以下位置的建筑，相應材料賦予飽和密度；而位于地下水位面以上位置的建筑，相應材料賦予材料測量密度。設置模型材料其他相關參數，在不對初始應力進行適當賦值條件下進行彈塑性求解，使模型達到默認的平衡狀態，從而獲得初始應力場。

2) 將處于地下水位面以下位置的建筑，相應材料賦予飽和密度；而位于地下水位面以上位置的建筑，相應材料賦予材料測量密度。在設置了合理的孔隙壓力分布時，設置模型材料其他相關參數，對初始應力進行適當賦值條件下進行彈塑性求解，使模型達到默認的平衡狀態，從而獲得初始應力場。

3 模型構建

圖1為試驗模型。砂柱高1 000 mm，砂柱直徑100 mm，砂土干密度1 700 kg/m3，砂土孔隙率0.3，飽和密度為2 000 kg/m3。沿高程設置孔壓監測點，設置兩種水位面高程，第一種情況水位面高程設置成1 m，砂柱全部位于水位面以下；第二種情況水位面高程設置成0.5 m，砂柱一半位于水位面以下，一半位于水位面以上。

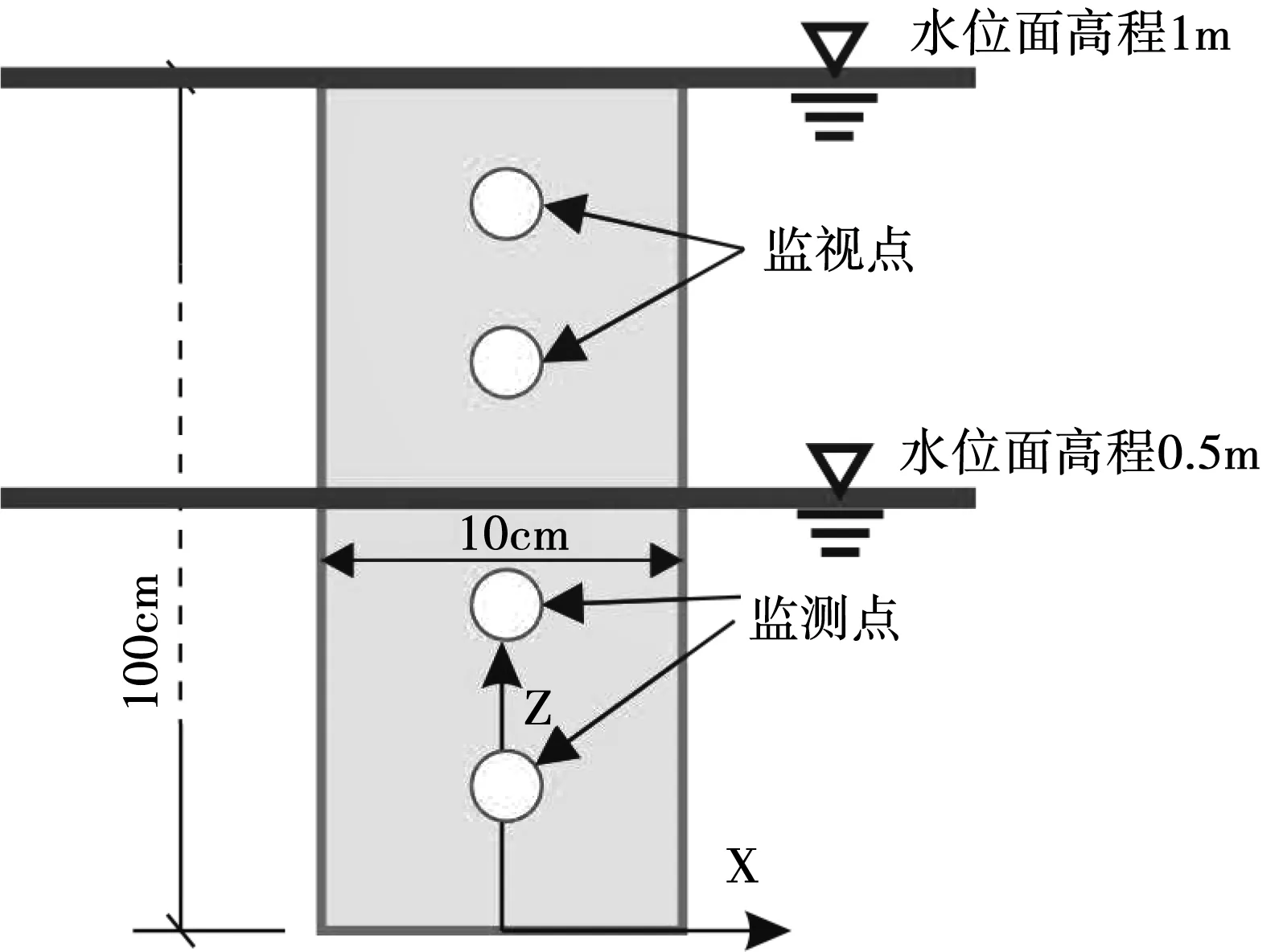
圖1 Liakopoulos砂柱試驗設置

4 計算結果

以下主要探討在對初始應力賦值和不賦值條件下，涉及變高程水位面條件下，初始應力場的生成區別。

4.1 不對初始應力進行賦值

在不對初始應力進行賦值條件下，分別模擬計算兩種水位面條件下獲得的初始應力場，結果見圖2。過程中直接對材料賦予其真實的彈塑性模型，并賦予真實的相關彈塑性材料參數，主要包括剪切模量、體積模量、黏聚力、抗拉強度、內摩擦角。首先對1 m高程水位面的砂柱進行初始應力場生成，將材料密度設置為飽和密度，獲得的Z方向初始應力場云圖見圖2(a)。由圖2(a)可知，在不設置初始應力值時，能夠獲得正確的初始應力場，計算共執行4 852步。然后對0.5 m高程水位面的砂柱進行初始應力場生成，將位于水位面以下材料密度設置為飽和密度，將位于水位面以上材料密度設置為干密度，獲得的Z方向初始應力場云圖見圖2(b)。由圖2(b)可知，在不設置初始應力值時，也能夠獲得正確的初始應力場，計算共執行6 584步。

圖2 不賦值初始應力時求解的初始應力場云圖

4.2 對初始應力進行適當賦值

在對初始應力進行賦值條件下，分別模擬計算0.5、1 m兩種水位面高程條件下獲得的初始應力場，結果見圖3。過程中同樣采用直接對材料賦予其真實的彈塑性模型，并賦予材料真實的相關彈塑性參數，主要包括剪切模量、體積模量、黏聚力、抗拉強度、內摩擦角。首先對1 m高程水位面的砂柱進行初始應力場生成，將材料整體密度設置為飽和密度，同時經過計算，對ZZ方向、XX方向、YY方向的初始應力進行適當合理賦值，最終獲得的Z方向初始應力場云圖見圖3(a)。由圖3(a)可知，在設置初始應力值時，也能夠獲得正確的初始應力場，計算共執行122步，幾乎未進行計算。然后對0.5m高程水位面的砂柱進行初始應力場生成，將位于水位面以下材料密度設置為飽和密度，將位于水位面以上材料密度設置為干密度，同樣經過計算，對ZZ方向、XX方向、YY方向的初始應力進行適當合理賦值，這里要特別注意計算結果的正確性，因為位于水位面以下位置處，砂柱的初始應力設置和水面以上位置處的設置并不相同，獲得的Z方向初始應力場云圖見圖3(b)。由圖3(b)可知，在設置初始應力值時，也能夠獲得正確的初始應力場，計算共執行106步，也幾乎未進行計算就達到了初始平衡狀態。相較于不對初始應力進行適當賦值時的情況，在對初始應力進行適當賦值時，計算效率提高，計算結果和軟件自行計算結果相同。

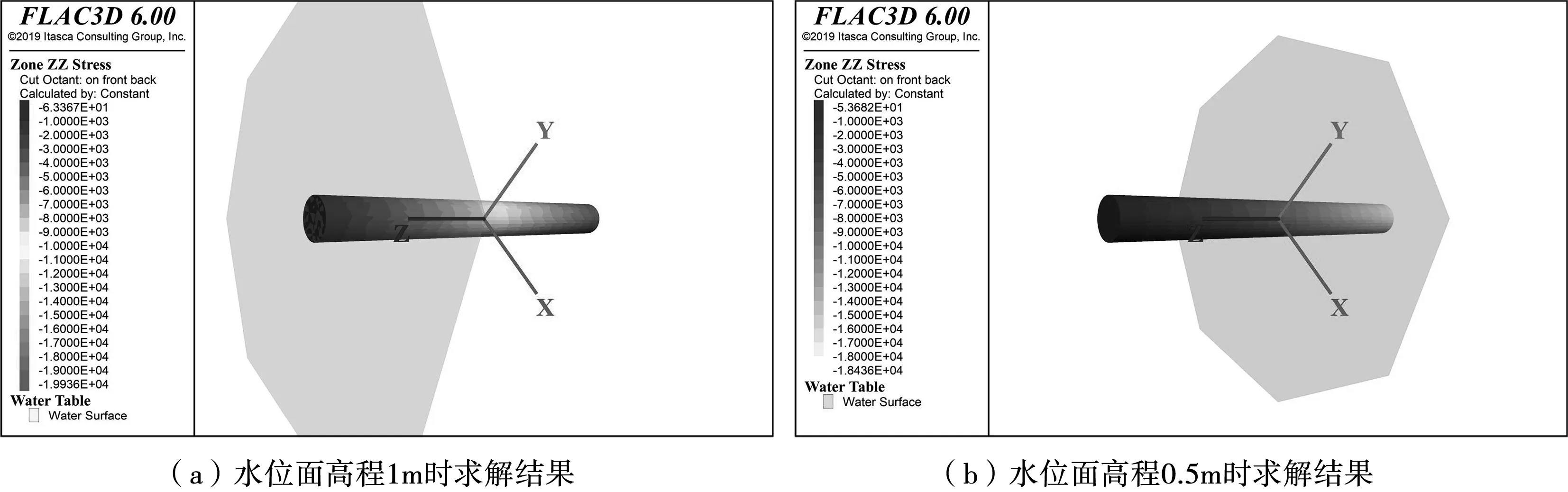
圖3 彈塑性模型變參數求解的初始有效應力場云圖

5 結 論

在對初始應力進行和不進行適當賦值時，通過對比不同高程水位面求解得到的初始應力場Z方向的應力場云圖，結論如下：

1) 在不對初始應力進行和不進行適當賦值時，直接進行彈塑性模型條件下的求解，均能夠獲得變高程水位面條件下與實際情況符合的初始應力場。

2) 相比于對初始應力進行適當賦值的情況，不對初始應力進行適當賦值能夠有效減少計算求解步數。

3) 建議采用不對初始應力進行適當賦值、直接彈塑性求解的方式生成涉及變高程水位面建筑的初始應力場。