基于改進CNN-LSTM的飛控系統剩余壽命預測

李夢蝶，趙 光，2，羅靈鯤，胡士強

1.上海交通大學 航空航天學院，上海 200240

2.中國商用飛機有限責任公司，上海 200126

故障預測與健康管理（prognostics and health management，PHM）是保障設備安全和優化維修策略的重要技術，現已在諸多領域得到應用。PHM 技術旨在利用傳感器數據評估系統健康狀態，為故障處理和維修決策提供支持[1]。在航空領域，飛機的維修方式已經從事后維修逐步發展成定時維修和視情維修相結合的預防性維修策略[2]。剩余壽命（remaining useful life，RUL）預測作為PHM 的核心技術，能夠監測飛機系統及其關鍵部件的退化程度。準確的RUL預測可以避免過度維修造成的成本浪費或維修不及時造成的安全性隱患，因此開展RUL預測方法的研究對預防性維修策略的制定有重要的指導意義[3]。

設備的RUL預測方法主要分為三大類[4]：模型驅動法、數據驅動法以及模型數據混合驅動的方法。模型驅動法通過建立系統或部件的物理失效模型[5]來預測RUL，建模有助于加深對系統失效機理的理解。但由于實際運營過程中的變化因素復雜，模型驅動法一般無法考慮到系統當前狀態并進行模型更新，因此難以做出動態的預測。數據驅動法利用退化監測及壽命的大量樣本，給出系統未來健康狀態或剩余壽命的預測。數據驅動法通過記錄當前狀態作為新的樣本，不斷調整自身參數，以實現動態預測，并使得預測更加準確。在數據驅動的RUL 預測方法研究中，現存的一大問題是不易獲取大量“運行至失效”的訓練數據。其他預測問題也常存在數據集缺乏的問題，常用的數據生成方法包括生產對抗網絡[6]、元學習[7]等，可以根據小樣本數據完成網絡的訓練。然而在航空領域，對于RUL預測問題，即使是小樣本的真實數據依然屬于航空公司隱私，因此這類方法并不適用。目前部件層級的壽命數據常通過加速試驗或飛行試驗獲取，獲取成本高昂。模型和數據混合驅動的方法[8-9]則將模型與數據方法結合起來，根據對系統的理解構建仿真模型并生成數據集，再基于數據驅動實現動態預測。因此本文采用模型和數據混合驅動的RUL預測方法，以發揮各自方法的優勢。

模型驅動法可以分為兩類：數學建模法和仿真建模法。數學建模法指建立系統的失效傳播模型，如裂紋傳播模型等，從微觀層面推導公式來計算RUL，但不適合為復雜系統的RUL預測提供數據幫助。仿真模型則從宏觀層面出發，建立系統相關模型，模擬隨機退化狀況[10]，生成大量數據樣本，為數據驅動的預測提供基礎。利用仿真模型獲取數據是解決諸多領域數據缺乏問題的常用方法，現有較成熟的研究是NASA通過對航空發動機仿真建模來模擬發動機系統的故障傳播過程獲取“運行至失效”的壽命數據，產生了航空推力系統仿真（commercial modular aero-propulsion system simulation，C-MAPSS）[11]數據集，被廣泛用于數據驅動的RUL預測研究中。國內也有許多學者在發動機性能退化仿真和飛控系統的故障數據生成方法進行了相關研究。現有飛控系統仿真數據生成的研究仍存在難以模擬系統的退化過程，并判斷系統失效時刻來獲取剩余壽命標簽的問題。

基于數據驅動的RUL 預測方法主要分為兩大類：基于統計概率的方法和基于機器學習的方法[12]。基于統計概率的方法包括貝葉斯網絡[13]、維納隨機過程[14]等。首先構建合適的健康指示因子（health index，HI）函數，選擇合適的統計分布假設來描述HI 函數的退化趨勢，根據大量退化數據選取合適的分布參數，最終計算出系統剩余壽命的概率。然而傳統概率方法的參數量有限，因此隨著退化數據維度和長度的增加，基于統計概率的方法難以提升RUL的預測準確性。而基于機器學習的研究可以解決多維數據非線性擬合的準確性問題，因此引起了廣泛關注。

近期，基于機器學習的RUL預測方法相關研究中，主要包括淺層機器學習和深度學習的方法。淺層機器學習包括淺層神經網絡[15]、支持向量機[16]等；深度學習網絡比淺層機器學習方法結構更復雜，參數量也更多，預測結果也更準確，因此本文采用了深度學習框架。胡昌華等[17]對基于深度學習的復雜退化系統RUL 預測進行了綜述性研究，闡述了四種典型深度學習技術在RUL預測的優缺點。Babu等[18]將CNN的卷積和池化層運用在時間維度上來提取多維傳感器數據的時序特征，進行故障特征提取和RUL預測。但CNN的特征提取更重視局部特征，可能導致整體信息的丟失，RNN網絡獨特的遞歸結構可以幫助記憶和傳遞后向信息，便于處理時序數據。Heimes[19]利用擴展卡爾曼濾波（extended Kalman filter，EKF）以及遺傳算法自動迭代優化RNN 神經網絡參數，用于航空發動機公開數據集的RUL預測，獲得了當時的最佳預測成績。然而由于RNN網絡反向傳播過程存在梯度爆炸或梯度彌散的問題，帶有門結構的長短時記憶網絡（long short-term memory，LSTM）[20]作為一種RNN 的改進算法被提出，適用于長序列時間數據的處理。Zheng等[21]證明了兩層LSTM網絡和兩層前饋神經網絡的組合，對多維長序列時間數據的預測能力優于BABU所提出的CNN網絡。Wu等[22]對比了帶有遺忘門的LSTM、標準RNN 以及門循環單元（gated recurrent unit，GRU）對RUL的預測效果，證明了LSTM網絡的優越性。但是由于RUL預測問題不同于一步時間序列預測問題，其訓練樣本是包含了空間和時間結構的序列，因此LSTM 網絡在RUL 預測方面仍然存在缺點，即容易忽略多維傳感器之間的空間關聯特征，而可能忽略空間上的部分故障信息。

結合上述分析以及前沿技術在本文研究任務中存在的問題，本文采用仿真模型生成數據集，并選擇LSTM網絡進行RUL預測。綜上所述，本文主要貢獻有以下幾個方面：

（1）針對系統退化仿真數據集的生成問題，給出了模型驅動的失效數據集生成流程，利用蒙特卡羅（Monte Carlo，MC）仿真解決了剩余壽命標簽的獲取問題，為數據驅動的RUL預測提供了數據基礎。

（2）針對LSTM 網絡在RUL 預測上空間特征提取不充分的問題，提出了1D-CNN-LSTM 的RUL 預測算法，并結合滑動窗口解決了訓練樣本不充分、維度不統一的問題，進而提高了算法的預測準確率。

1 模型驅動的失效數據集生成

針對系統退化仿真數據集如何生成的問題，本文提出了模型驅動的失效數據集生成方法，流程如圖1 所示。首先根據系統的架構以及系統組成部件的數學表達式構建對應的Simulink模型；其次分析系統的典型故障模式，包括各部件的漸進型故障和突發型故障等，對故障模式進行建模并將故障注入原系統得到退化仿真模型；最后基于蒙特卡羅仿真生成隨機故障時間樣本，按照時間樣本的序列依次注入故障，根據故障判據判斷系統響應是否超出失效閾值，記錄仿真失效時刻所對應的故障樣本時間，作為系統的失效壽命數據；退化仿真模型最終的輸出是真實系統中可采集到的多組傳感器的時間序列退化數據以及記錄的系統失效壽命數據。

1.1 基于Simulink的退化模型構建

RUL預測不只是單純地預測數據未來值，而是在此基礎上預測系統中長期的性能衰退趨勢以及距離失效的剩余時間。考慮到復雜系統各組成部件之間存在著冗余、耦合的高度集成關系，部件退化不一定會導致系統的失效，若僅考慮部件級的退化來進行維修決策可能造成維修資源的浪費。因此，需要通過系統建模仿真來評估部件級退化造成系統級性能退化的程度。

根據系統數學表達式和故障模式的特征表達式，可以搭建系統及其故障模式的Simulink 模型。此處不再贅述建模過程，而是更關注如何構建基于Simulink的系統退化模型。

本文利用MATLAB 和Simulink 給出了一種故障注入和退化模型的構建程序，如圖2所示。在原輸出與故障模式輸出之間添加Simulink 模塊庫中的可變子系統“Variant Subsystem”，將故障模型和無故障模型添加到可變子系統內；接著在可變子系統的參數設置中為每一故障模式定義變體控制變量，并對定義的每一個控制變量設置唯一的控制條件，通過在MATLAB 中改變控制條件即可達到選擇故障模式的目的。

利用故障模式建模表征部件的退化程度，通過控制故障注入程序，按照下一節的方法即可模擬系統在多種故障模式下的隨機退化傳播過程，達到構建系統退化模型的目的。

1.2 基于MC仿真的失效壽命數據獲取

在構建了系統退化模型基礎上，仍需解決系統隨機故障時間及序列生成和失效時刻標簽的獲取問題。基于MC仿真的隨機故障時間樣本生成方法如下：假定系統組件故障概率服從指數分布，首先借助蒙特卡羅方法生成（0，1）之間的均勻隨機數，并求解指數分布的反函數，綜合（0，1）區間上的均勻隨機數和反函數變換法產生服從指數分布的隨機數。

記隨機變量R 在（0，1）區間上服從均勻分布，部件故障時間t 是一個非負的隨機變量，服從失效率為λ 的指數分布，則隨機變量t 的概率密度函數為：

其對應的分布函數為：

如果隨機變量t的分布函數F(t)連續，則R=F(t)是（0，1）區間上均勻分布的隨機變量，取對數解得：

借助MATLAB 的rand 函數生成（0，1）區間上均勻分布的隨機變量R，代入部件故障模式的失效率，即可生成服從指定分布的隨機故障時間t。

蒙特卡羅仿真常被用于基于模型的安全性分析[23]中，根據概率分布隨機抽樣，生成系統各部件的隨機故障時間樣本[24]，模擬部件不同故障模式的發生時刻；然后將時間樣本對應的故障序列注入系統退化模型，模擬在不同風險場景下的系統響應，評估系統的各類性能指標是否符合性能要求的閾值范圍，得到仿真失效時刻的時間樣本值用于計算剩余壽命標簽。退化仿真模型的建立和剩余壽命標簽的獲取為數據驅動的RUL預測提供了數據基礎。

2 基于CNN-LSTM的RUL預測算法

針對LSTM 算法在時空結構數據的RUL 預測中提取空間故障信息不充分的問題，提出了1D-CNN-LSTM網絡，結構如圖3 所示，該網絡既保證了LSTM 在預測時序數據時的優勢，同時結合1D-CNN提取傳感器之間的空間關聯特征，以提高預測準確率。

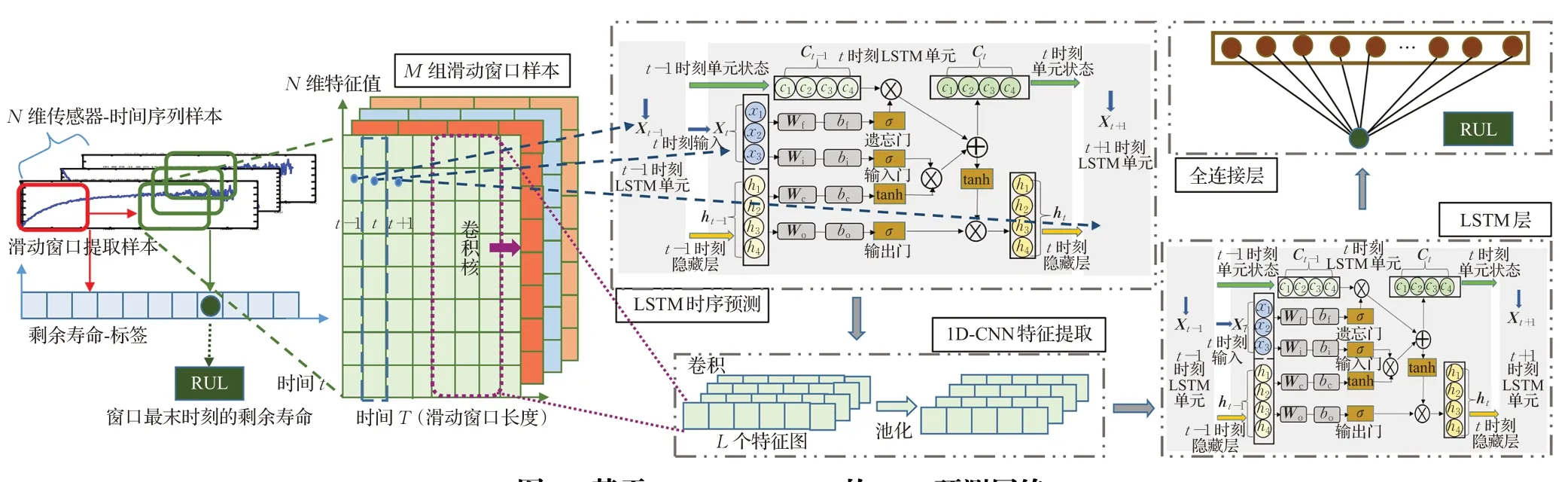
圖3 基于1D-CNN-LSTM的RUL預測網絡Fig.3 RUL prediction network based on 1D-CNN-LSTM

針對RUL預測問題中每一組“運行至失效”數據樣本長度不等、總樣本量有限的問題，采用了滑動窗口法提取等時間長度的數據樣本以增加樣本數量，從而減小網絡的訓練誤差。如圖3所示，樣本中傳感器的特征維度為N，滑動窗口的長度為T，滑動步長為1，提取的每一組樣本尺寸為T×N,即可獲得M組等大小的滑動窗口數據樣本，每一組樣本對應窗口的最末時刻的一維剩余壽命值，所提取的滑動窗口樣本作為網絡輸入，對應剩余壽命值作為網絡輸出標簽。

2.1 1D-CNN特征提取

CNN網絡[25]相比于傳統特征提取方法，在局部特征的提取上獲得了很高的準確率，其權值共享的卷積核結構減少了訓練參數，池化操作可以降低數據的維度。不同維度的CNN 方法在處理數據的方法上大致相似，區別在于卷積核的尺寸設置，以及其如何在數據上滑動。1D-CNN 的卷積核只在時間維度上滑動，2D-CNN 的卷積核在時間和空間的平面上按S 型滑動，如圖4 為步長為1 的1D-CNN 和2D-CNN 卷積方式的區別，卷積核大小分別為8×3和3×3。

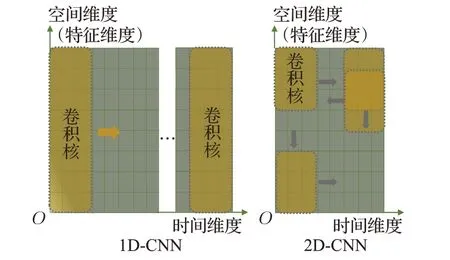
圖4 1D-CNN和2D-CNN卷積方式區別Fig.4 Difference between convolution way of 1D-CNN and 2D-CNN

從圖4中可以發現1D-CNN的卷積核能夠對空間維度上所有的特征進行卷積，而2D-CNN可能忽略距離較遠的特征之間的關聯特征。考慮到RUL預測問題的輸入為多維傳感器，若使用2D-CNN 進行特征提取，則在數據預處理時應當盡量將具有關聯故障信息的傳感器鄰近排布，人工經驗可能對預測結果造成一定程度的影響。

因此本文選擇1D-CNN 進行多維傳感器數據的特征提取，第一層LSTM網絡的輸出作為1D-CNN網絡的輸入，經過卷積和池化后再輸入到第二層LSTM 網絡，保證了時序和空間信息的完整性。

2.2 LSTM時間序列預測

長短時記憶網絡（LSTM）在時序預測方面的準確率較高。LSTM 是循環神經網絡（RNN）的一種特殊變體，它通過引入遺忘門ft、輸入門it和輸出門ot來保存或遺忘當前信息，以達到長期記憶的功能。LSTM三組門單元的計算公式如下：

式中，Wf、Wi、Wo、WC和bf、bi、bo、bC分別為遺忘門、輸入門、輸出門、細胞單元（cell）的權重系數矩陣和偏置矩陣。上一時刻隱藏層的輸出ht-1與當前時刻輸入xt組合成新向量，與對應權重系數矩陣相乘，并加上對應偏置矩陣后，經過激活函數，即可得到對應門單元輸出。

隱藏層ht和LSTM的細胞單元Ct分別用于儲存短期記憶和長期記憶，計算公式如下：

遺忘門ft可以有選擇地遺忘上一時刻細胞單元的信息，與輸入門it和C~t求和后，共同決定當前時刻細胞單元狀態的更新，輸出門和當前時刻細胞單元狀態的卷積決定了隱藏層的更新。

圖5給出了t時刻的LSTM cell 的數學架構圖，每個cell 中包含了4 個節點（unit），輸入的序列特征維度為3。LSTM 通過細胞單元狀態和隱藏層傳遞時序信息，并在時間維度共享權重系數，經過多個時間步長后，輸出可以是最后一個時刻的隱藏層狀態值或所有時刻的隱藏層狀態值。

圖5 t 時刻的LSTM數學架構Fig.5 Mathematical architecture of LSTM at time t

在1D-CNN-LSTM 網絡中第一層LSTM 網絡輸出為所有時刻的隱藏層值，并作為1D-CNN 網絡的輸入，這樣可以更好地保存時序信息；第二層LSTM網絡輸出為最后一個時刻的隱藏層以簡化網絡，輸入到全連接層，最終輸出一維標簽值。此外為防止過擬合，在每層LSTM網絡后添加了Dropout層，隨機丟失一些節點權重。

針對LSTM 空間信息提取不足的問題，文獻[26]使用了2D-CNN展平和LSTM層并聯的雙通道結構，將兩個通道網絡的輸出展平并求和。該方法一方面需要保證網絡的維度相等，增加了算法的復雜度；另一方面2D-CNN 和展平層可能導致信息的丟失和混亂。而本文提出的1D-CNN-LSTM 網絡在解決LSTM 空間信息提取不足問題的同時，簡化了網絡結構，避免了不必要時序信息的丟失，提高了算法的預測準確率。

3 仿真及實例

本文以某型號飛機的橫側向飛行控制系統為例，選取典型故障模式進行故障注入，并結合MC仿真生成了仿真失效數據集，將其與數據驅動的RUL 預測領域得到廣泛應用的公開數據集進行了對比，論證了本文數據生成方法能夠生成具有統一標準的失效數據集，可用于不同系統的數據驅動RUL 預測。本文論述了基于1DCNN-LSTM 的RUL 預測步驟，并開展了公開數據集的RUL預測實驗，討論了方法中滑動窗口長度選取對預測準確率的影響，通過與其他網絡的預測結果對比，驗證了本文提出的1D-CNN-LSTM網絡預測的準確性。

3.1 仿真模型設置

選取某一型號飛機的雙通道三余度橫側向飛行控制系統進行建模分析[27]，結合Simulink工具對飛控系統的每一部件單獨建模，最后根據系統架構進行綜合與集成，系統架構如圖6所示。

圖6 某型號飛機橫側向飛行控制系統架構Fig.6 Architecture of a lateral flight control system

考慮橫側向飛控系統機電部件[28]的漸進型故障具有逐漸演變的趨勢，可能不會使得系統立刻失效，但隨著故障程度的加深會造成一定危險，可以用來表征系統的退化趨勢。表1 給出了飛控系統的典型故障模式及其參數[29]。按第2章所提方法進行故障注入即可得到系統退化模型，此處不再贅述。

為了確定系統的失效狀態，得到失效時刻標簽，應根據系統功能性質和所關注性能要求的重要程度來決定故障判據。本文采用體軸滾轉角φ(t)作為性能指標，ΩZ為系統未失效(R)的狀態集合，與其對應的故障判據為：

式中性能指標的閾值范圍[23]取值為：

仿真所選取的工況是巡航階段，假設飛機處于巡航階段，所處狀態點速度為178 m/s，迎角為0.216 rad，巡航高度10 668 m，架構評估時間20 s。滾轉命令為幅值0.2 rad，周期0.1 Hz 的方波信號。通過比較隨機故障序列注入后的性能指標值與無故障構型下理想值的差值是否超出給定范圍，可以判斷系統是否失效，并記錄系統失效時刻。

3.2 仿真失效數據集分析

利用MC 仿真生成100 組隨機故障時間，重復兩次分別作為訓練集和測試集，將每一部件每一種故障模式按照式（3）的故障發生時間依次排序后注入模型，直至系統故障判據失效，即可得到一個組別(id)的“運行到失效”數據。訓練集中是從正常到失效的完整周期內全部時間序列的采樣值，測試集中是失效前一隨機時間點之前的狀態參數值及其對應真實壽命。

表2為所生成的橫側向飛控系統退化數據集中每一列的含義。數據集中的退化數據是狀態空間參數的傳感器值，包括滾轉率、滾轉角、偏航率的三余度慣性測量元件（IMU）輸出和舵偏角的三余度位置傳感器輸出。其中，為了真實模擬工程情況，將仿真時刻t按比例映射到第2章所生成的隨機運營時間樣本空間中，得到運營時長T；模型中傳感器（IMU、位置傳感器）均為獨立的三個冗余架構，并根據傳統三余度表決算法選擇正確信號輸出；每一組別的最大運營時長即為該組別的壽命值，可用于計算RUL標簽。

表2 某型號橫側向飛控系統退化數據集Table 2 Degradation dataset of a lateral flight control system

為證明本文所生成的數據集在RUL預測方面的有效性，將其與航空發動機退化仿真C-MAPSS 的第一個數據集FD001 進行對比，該數據集在數據驅動的RUL預測領域受到了廣泛研究與應用。如表3所示，兩個數據集在構成上具有一致性，工況數和組別數相同，不過由于飛控系統和發動機系統本身存在差異性，且兩者冗余程度和安全性等級的設計要求不一致，兩個數據集之間也存在一些差異。

表3 飛控系統數據集與C-MAPSS數據集對比Table 3 Comparison between flight control system dataset and C-MAPSS dataset

（1）兩者相同之處在于：在C-MAPSS 仿真數據集中，發動機系統關鍵部件的單一故障模式持續擴散并傳播造成系統失效，對關鍵參數提取特征，能夠反映出此故障在系統中的傳播趨勢并進行RUL 預測；在飛控系統退化數據集中，某些突發故障或多種故障接連發生后根據故障判據可判斷系統失效。圖7 為單一故障下系統發生失效的滾轉角響應曲線。系統失效可以產生壽命標簽，失效可反映在狀態參數的變化中，通過提取狀態參數的變化特征即可進行RUL預測。

圖7 單一故障下系統發生失效的滾轉角響應曲線Fig.7 Roll angle response curve of system failure under certain single fault

（2）飛控系統失效數據集的特殊性在于：

①由于飛控系統為雙通道（兩臺主飛控計算機、兩組執行機構作動器）三余度（三冗余傳感器）架構，有一部分故障發生時，系統并未失效，因此其退化模型的可同時發生故障模式數較多，基于這類退化數據集的RUL預測更注重冗余架構下部件退化對系統剩余能力的影響。

②飛控失效數據集中的隨機性來源于故障模式的組合以及發生故障的時間不同；而C-MAPSS 數據集中的隨機性來源于發動機系統的初始磨損及各部件發生故障的程度不同。

（3）與公開數據集對比，飛控失效數據集的改進在于將仿真時刻t按比例映射到隨機運營時間樣本空間中，得到運營時長T。相比于C-MAPSS數據集利用仿真時間（cycle）來表示壽命，本文給出了仿真時間及更直觀的運營時間來表示壽命，符合工程實際。通過失效率的調整，可以使得時間T更加符合真實情況。

（4）實際應用上，更多的工程信息可以提高模型的仿真精度，從而提高仿真數據的真實性；部件的失效率越準確，仿真數據集與真實數據的差異也越小；采用系統設計模型來進行RUL預測有助于設計的改進。

綜上所述，按照本文方法生成的失效數據集和公開數據集有統一結構，能反映系統的隨機退化趨勢，包括數據驅動RUL預測所需的傳感器狀態參數數據和對應的壽命標簽。此外本文通過仿真時間到運營時間的映射，使得預測工作更貼合工程實際情況。因此，本文通過解決退化模型構建及其標簽獲取問題，為飛控系統的數據驅動RUL 預測提供了有效的數據基礎，且這一方法可以推廣到不同的航空復雜系統中。

3.3 基于1D-CNN-LSTM的RUL預測步驟

下面以公開數據集C-MAPSS 為例，基于1D-CNNLSTM方法進行RUL預測。主要步驟如下：

（1）篩選數據，選擇相對變化幅值較大的特征維度，它們的變化更容易反映當前系統的健康狀態。因此選擇了“仿真時間cycle；工況設置1、2；傳感器2、3、4、7、9、11、12、14、17、20”，共13維數據作為網絡的輸入。

（2）利用最大最小值歸一化法對每一特征維度的數據進行預處理，標準化公式如式（10），式中x為樣本，x*為歸一化后的樣本值：

（3）建立RUL 標簽作為網絡的輸出，每一時刻的RUL 代表系統還可以繼續運行的時間，一般認為其RUL是線性下降的，但由于數據集在隨機運行一段時間后才會發生故障，其初始RUL 應當保持不變。因此其RUL標簽應當為分段函數，圖8為組別1#發動機的RUL函數，根據文獻[19]對數據集的分析，選擇130 cycle 作為所有組別系統的初始壽命。

圖8 C-MAPSS數據集剩余壽命分段線性函數Fig.8 Piece-wise linear RUL function in C-MAPSS dataset

（4）利用滑動窗口提取多組訓練數據集（train_FD001）樣本輸入網絡，輸出為窗口最末時刻的RUL 標簽值，以窗口長度100 為例訓練網絡，網絡參數設置如表4。選取的優化器為“rmsprop”，一次迭代的樣本數量batch_size 為200，最大迭代批次epoch 為100，訓練集與測試集的分割比例為0.95∶0.05，訓練直至測試集的損失函數達到最小且連續在10 個批次不再減小，并保存最優模型，用于測試數據集（test_FD001）。在測試數據集中將每一組別的發動機數據與滑動窗口長度相等的最后一組樣本輸入最優模型，得到的輸出值即為該組發動機的預測壽命。

表4 1D-CNN-LSTM網絡參數Table 4 1D-CNN-LSTM network parameters

（5）為了評價預測算法的準確性，根據測試數據集（test_FD001）的預測RUL 和真實RUL（RUL_FD001）的差值計算預測算法的得分，得分越低，則預測誤差越小，預測效果越好。式（11）為該數據集的官方評價指標[11]。對N組發動機系統的誤差計算得分并求和后可得到整個數據集的總得分，相比于低估RUL，高估RUL可能造成的風險更大，因此誤差大于0的懲罰系數比誤差小于0時高。

3.4 預測結果與討論

由于不同滑動窗口的值會影響輸入數據的維度，從而影響預測效果，選擇了不同長度滑動窗口及網絡架構（LSTM網絡為雙層，分別為32節點和64節點）[21]進行預測，結果如表5 所示。其中，由于測試集的組別數據會在隨機時間結束，其最小周次數據為31 cycle（見表3），存在滑動窗口長度大于某些組別數據長度的情況，而訓練模型的輸入維度等于窗口長度，這些組別的數據為不可測試單元。因此，表5給出了不同滑動窗口長度下的可測試單元數（最多100組），預測總得分以及平均得分。

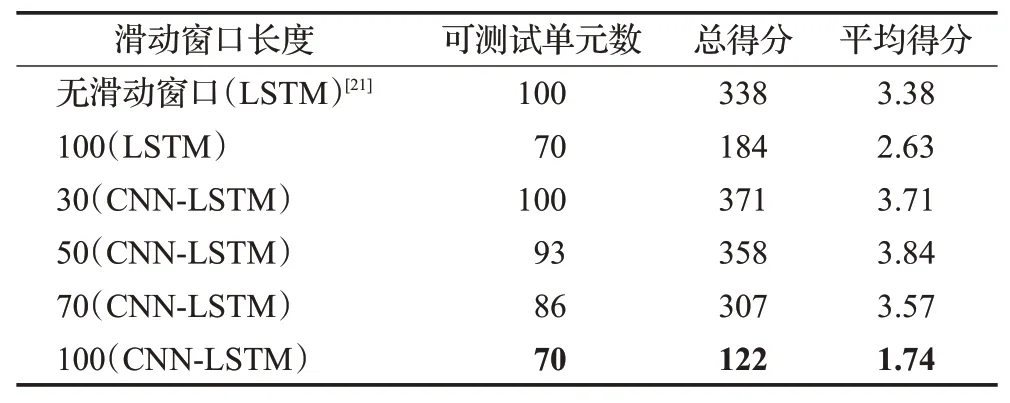
表5 不同窗口長度下的RUL預測結果Table 5 RUL prediction results with different window lengths

由表5可以做出以下分析：

（1）在相同的網絡架構下，添加滑動窗口可以減小預測誤差，由于利用滑動窗口法增加了訓練數據樣本，使得LSTM網絡獲取到更多的故障信息。

（2）滑動窗口的長度越長，平均得分越低，這是由于較長的輸入維度為LSTM網絡提供了更多的長期記憶，且長序列相比短序列包含的故障信息更多，短序列更加難以預測到未來的退化趨勢和RUL。

（3）在相同的滑動窗口長度下，添加了1D-CNN 的網絡比單獨的LSTM 網絡預測誤差更小，這證明了1DCNN 網絡可以有效地提取傳感器之間的關聯信息，提高預測準確性。

圖9為滑動窗口長度均為100 的LSTM 網絡和1DCNN-LSTM 網絡在測試集上的預測效果，橫坐標為測試集組別號，縱坐標為降序排列的剩余壽命，分別為同一組別剩余壽命的真實值和預測值。圖10為兩個網絡的預測誤差分布圖。分析可知，當RUL 越接近0 時，預測誤差越小；加了1D-CNN 的LSTM 網絡預測誤差更小，誤差接近0 的比例更高，證明了1D-CNN-LSTM 網絡比LSTM網絡有更高的預測準確性。

圖9 兩種網絡架構下的RUL預測誤差Fig.9 RUL prediction error under two different networks

圖10 兩種網絡架構下的預測誤差分布Fig.10 Prediction error distribution under two networks

將本文預測結果與其他相關RUL預測方法在該數據集的預測結果進行了對比，如表6所示。與多層感知機（MLP）、卷積神經網絡（CNN）、循環神經網絡（RNN）相比，LSTM 網絡對RUL 的預測誤差明顯更小；與另外兩種既考慮了時間又考慮了空間的GCN-TCN 方法和將CNN 和LSTM 網絡展平后并聯的DAG 方法相比，本文的預測平均誤差更低。上述實驗證明本文所提出的滑動窗口法和1D-CNN-LSTM網絡平均誤差很小，對較長的時間序列預測準確性明顯優于其他方法。

表6 不同方法RUL預測結果對比Table 6 RUL prediction results with different methods

4 結束語

本文提出了一種模型和數據混合驅動的RUL預測方法。首先，針對系統退化仿真數據集的生成問題，給出了模型驅動的失效數據集生成流程，利用蒙特卡羅仿真解決了剩余壽命標簽的獲取問題，為數據驅動的RUL預測提供了數據基礎；其次，針對LSTM算法在RUL預測上空間特征提取不充分的問題，提出了滑動窗口法和1D-CNN-LSTM算法，提高了算法的預測準確率；最后，以某型號飛機的橫側向飛行控制系統為例，利用模型方法生成了仿真失效數據集，與C-MAPSS 公開數據集對比，證明了本文所提出的數據集生成方法有效；基于本文提出的深度學習預測算法在公開數據集上進行RUL預測實驗，且與已有預測方法進行了對比，結果表明本文的預測算法準確度較高。因此，本文結合了模型和數據驅動的RUL 預測的綜合優勢，為不同系統的RUL 預測提供了新的研究思路，工程上將對維修策略的制定有很大幫助。