Two-parameter logistic模型的Gibbs抽樣敏感度分析
----基于Pólya-Gamma分布

付志慧, 山丹丹, 周 末, 王立柱

(1. 閩南師范大學 數學與統計學院, 福建 漳州 363000;2. 沈陽師范大學 數學與系統科學學院, 沈陽 110034;3. 福建省粒計算及其應用重點實驗室, 福建 漳州 363000;4. 福建省數據科學與統計重點實驗室, 福建 漳州 363000)

0 引 言

目前,大部分基于logistic項目反應模型的MCMC[1-2](markov chain monte carlo)估計方法主要是利用MH(metropolis-hastings)算法[3]來實現,然而,MH算法需要在生成馬氏鏈的每一步計算接受概率或拒絕概率,這樣會影響收斂速度。相對而言,由Gibbs抽樣方法產生的馬氏鏈上的值都會保留下來,大大提高了收斂速度[4-5]。近年來,很多學者研究了項目反應模型的Bayes估計方法[6]。1995年,Chib[7]將Gibbs抽樣方法和MH算法相結合,對2PL模型和3PL模型(three-parameter logistic item response model)進行比較,并給出了MCMC估計。在教育與心理測量領域,1992年,Albert[8]首次將Gibbs抽樣方法應用于兩參數正態卵形模型中。1999年,Patz等[9]研究了MCMC在三參數IRT模型中的應用,并討論了缺失數據問題。然而,對于2PL模型,上述大部分抽樣方法都要結合MH算法,降低了估計效率和收斂速度。針對常用的廣義線性模型----logistic模型,2013年,Polson等[10]提出了一種新的基于Pólya-Gamma分布的數據增加抽樣方法。在此基礎上,2019年,Jiang[11]首次將該方法應用到心理測量理論的2PL模型中,推導了基于Pólya-Gamma潛變量分布的Gibbs抽樣方法,其收斂速度和效率要優于MH算法。

在項目反應理論(item respond theory, IRT)[12]背景下,人們普遍認為需要較大的樣本容量才能準確估計模型參數,這使得IRT在小樣本的情況下不太適用[13]。然而,貝葉斯分析的優勢在于對模型參數假定合適的先驗分布,從而對小樣本數據集也可以得出較準確的參數估計結果。本文在隨機模擬實驗部分進一步驗證了這一結論。具體地,本文通過模擬發現,即使是對于相對較小的樣本量n=100,較長的測驗長度I=40,得出的估計誤差也不是很高----區分度參數a的RMSE在0.2左右,難度參數b的RMSE在0.4左右。另外,在本文的模擬實驗設置下,發現采用較精確的先驗分布(N(0,1))可以得出比較準確的估計結果。

1 2PL模型和Pólya-Gamma分布介紹

假設有n個被試者,I個項目,yij表示第j個被試者回答第i個項目的得分,yij=1表示回答正確,yij=0表示回答錯誤。令pij表示第j個被試者對第i個項目回答正確的概率, 2PL模型表達式為

其中:j=1,2,…,n;i=1,2,…,I;ai表示項目i的區分度參數;θj表示第j個被試者的能力參數;bi表示項目i的難度參數。

本文需要引進潛變量分布----Pólya-Gamma分布,它是Gamma分布的無限混合。具體地,設X為一個隨機變量,其中b>0,c∈R為分布參數,若

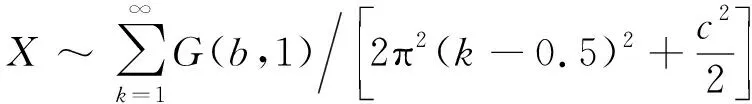
(1)

則稱X～PG(b,c)。

2 潛變量的引進和抽樣過程

即wij|·～PG(1,ai(θj-bi))。其中:被試者j=1,2,…,n;項目i=1,2,…,I[11]。

從而得到各參數的滿條件分布,θj的滿條件分布為

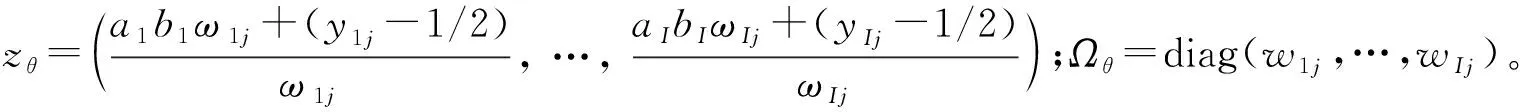
bi的滿條件分布為

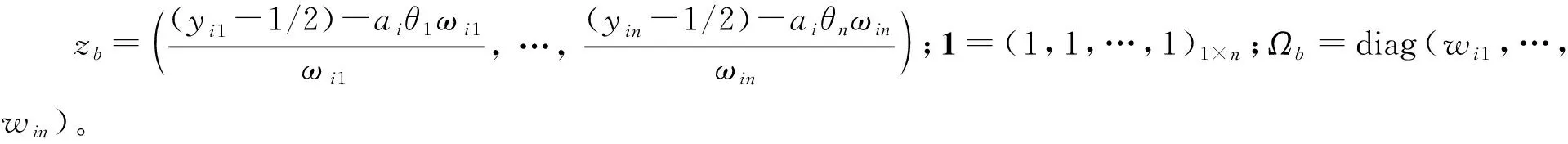
ai的滿條件分布為

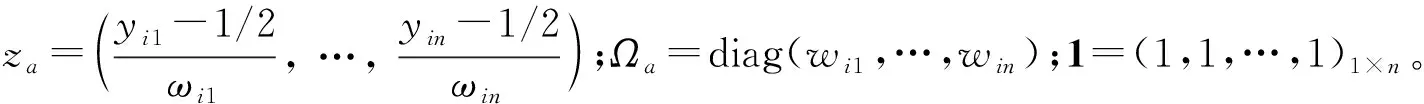
3 模擬實驗

本節主要針對2PL模型通過模擬實驗對基于Pólya-Gamma的抽樣方法進行敏感度分析。考慮的指標有樣本容量(sample size)、測驗長度(test length)以及題目參數先驗分布的選擇(prior specification),具體取值見表1 。

表1 模擬實驗設計Table 1 Simulation experiment design

本文使用RMSE和BIAS來評估項目參數估計的準確性,具體定義為

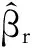
4 實驗結果分析

表2和表3分別得出了區分度參數a和難度參數b的估計結果。 所得結論總結如下:

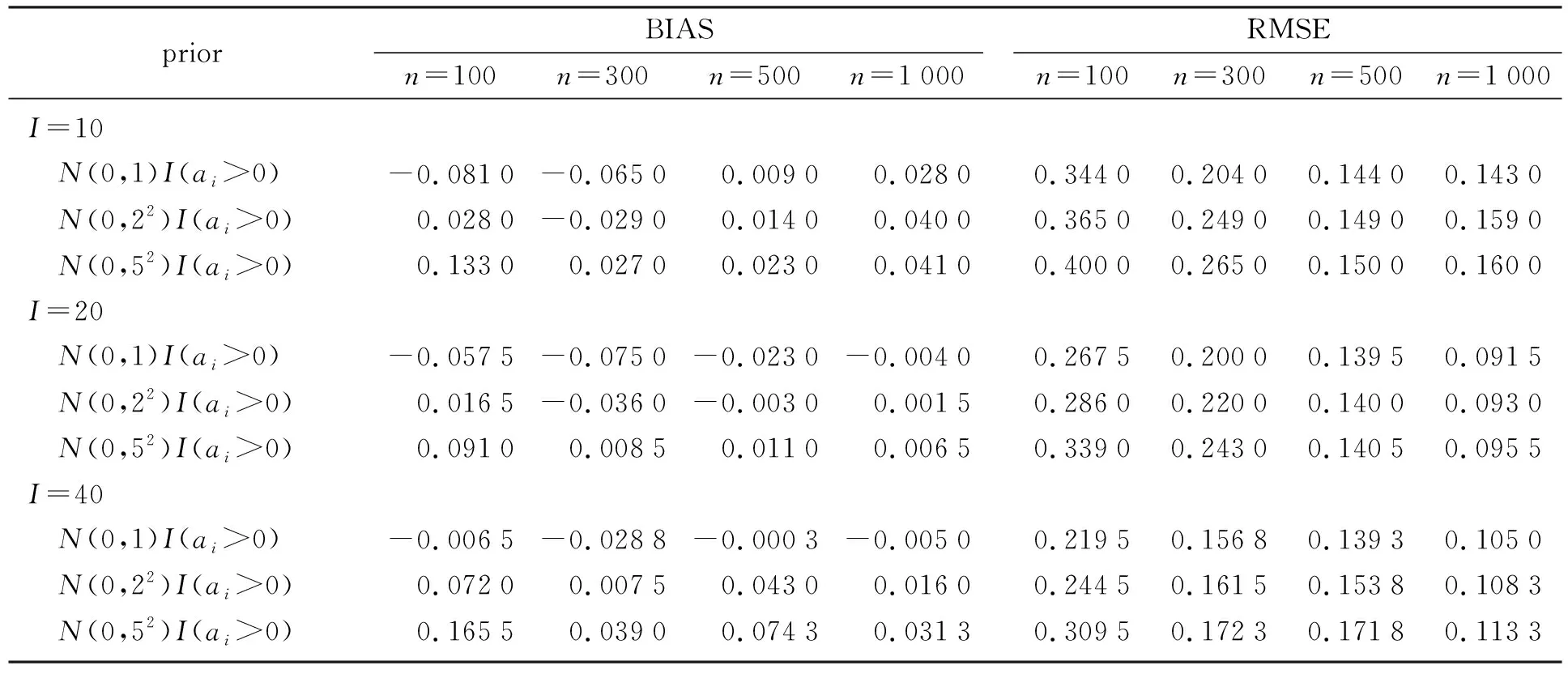
表2 區分度參數a的RMSE和BIASTable 2 RMSE and BIAS of the discrimination parameter a

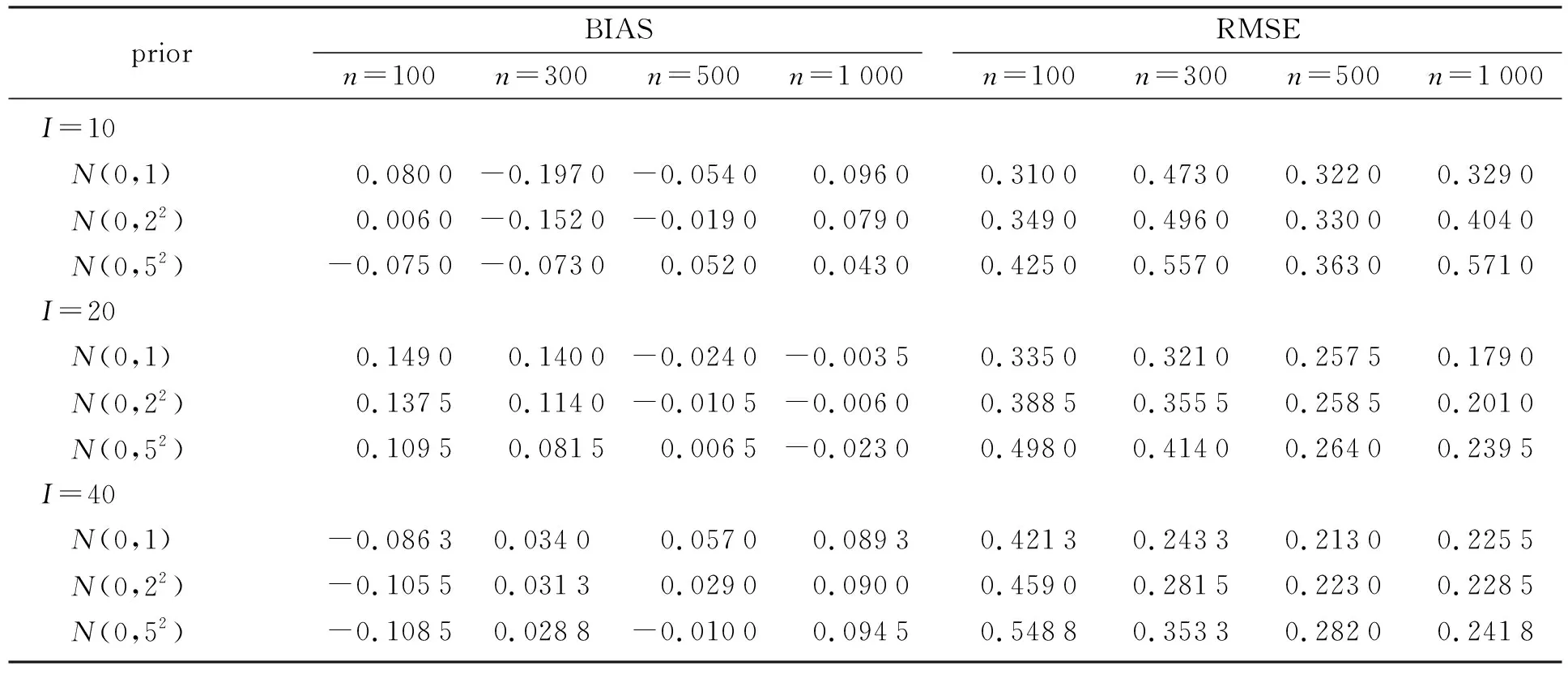
表3 難度參數b的RMSE和BIASTable 3 RMSE and BIAS of difficulty parameter b

1) 對于題目區分度參數a,隨著樣本容量n的增加,RMSE逐漸減小。具體地,在先驗為N(0,1)I(a>0)、測驗長度I為20時,被試個數n為100,300,500,1 000對應的RMSE分別為0.267 5,0.200 0,0.139 5,0.091 5。同時,隨著測驗長度I的增加,RMSE也逐漸減少。例如:在先驗為N(0,1)I(a>0)、被試n為500時,測驗長度I為10,20,40對應的RMSE分別為0.144 0,0.139 5,0.139 3。

2) 同樣地,對于題目難度參數b,隨著樣本容量n的增加,RMSE也逐漸減小。具體地,在先驗為N(0,1)、測驗長度I為20時,被試個數n為100,300,500,1 000對應的RMSE分別為0.335 0,0.321 0,0.257 5,0.179 0。同時,隨著測驗長度I的增加,RMSE也逐漸減少。例如:在先驗為N(0,1)、被試n為500時,測驗長度I為10,20,40對應的RMSE分別為0.322 0,0.257 5,0.213 0。

3) 在不同的先驗假定下,隨著先驗方差的增加,對應參數的RMSE增大。具體地,對于區分度參數a,在先驗為N(0,1)I(a>0)、測驗長度I為40時,被試個數n為100,300,500,1 000對應的RMSE分別為0.219 5,0.156 8,0.139 3,0.105 0。在先驗為N(0,22)I(a>0)、測驗長度I為40時,被試個數n為100,300,500,1 000對應的RMSE分別為0.244 5,0.161 5,0.153 8,0.108 3。在先驗為N(0,52)I(a>0)、測驗長度I為40時,被試個數n為100,300,500,1 000對應的RMSE分別為0.309 5,0.172 3,0.171 8,0.113 3。

4) 對于題目區分度參數a,BIAS的絕對值最高為0.165 5,最低為0.000 3。對于題目難度參數b,BIAS的絕對值最高為0.197 0,最低為0.003 5。這些偏差結果都是可以接受的。

5 結論及展望

本文主要針對2PL模型,對基于Pólya-Gamma分布的Gibbs抽樣方法進行了模擬研究,分析了在不同實驗設置下的估計效果。結果發現,隨著樣本容量和測驗長度的增加,估計結果的精確性有所提高。同時,在先驗方差取值較小的情況下,得到的估計結果相對準確。本文的模擬實驗設置僅討論了樣本容量n為100,300,500,1 000的情況,對于較大的樣本容量,如n為5 000,10 000的情況并沒有考慮,這將作為我們下一步的研究內容。這種高效的Pólya-Gamma抽樣方法也可以應用到3PL模型[14]及等級項目反應[15]等多級評分模型中。