油田注水管網水力模擬研究

祝洪偉 高 勝 任永良 何樹威 王 妍 許彥飛

（東北石油大學機械科學與工程學院）

在油田注水管網的運行過程中，常因管道的流量變化、泵站運行參數的改變及管網的漏損等因素使管網的水力條件發生改變，不利于油田管網的正常高效運行［1］。另外，油田注水管網系統地理跨度大、結構復雜，不宜直接在實際管網上進行大量試驗。 通過建立與注水管網系統等效的實驗管網， 對實際注水管網系統進行模擬優化，可以極大地節約研究時間、成本和能耗。 筆者通過研究管流變態模擬相似理論，保證油田注水管網系統與實驗管網的主要作用力相似，即壓力和阻力都相似，推導出其在幾何、動力變態相似的條件下，實驗管網與油田實際管網物理量之間的相似關系。 并利用運動相似準則驗證等效的實驗管網與管網原型的相似性。 此外，張新波等采用鍍鋅鋼管搭建供水管網實驗管網，但實測與變態模型計算結果相差較大，究其原因是在模型簡化過程中管網比尺和變態率的確定上引入了較大誤差，但限于現有實驗室空間、管材規格等實際條件，實驗管網模型微縮比尺只能取在這樣一個水平，使模擬的準確性大幅降低［2］。并且由于鋼管材質的實驗管網微縮比尺一旦確定就無法更改，因此只能模擬某個確定的系統管網， 具有局限性。高壓膠管材料具有占地面積小、管道長度可靈活選定、可變徑及可拆卸等優點，可以使實驗管網的比尺和變態率選定有更大的空間，增強模擬的準確性，另外為使實驗管網可以對多個油田注水管網系統進行相似模擬，筆者選用高壓膠管材料作為實驗管網的長輸管道。 通過單管線壓降實驗，應用不同沿程阻力損失公式對高壓膠管的壓力損失性質進行分析，為在實驗室條件下模擬油田注水管網系統運行提供一種新的科學途徑。

1 管網的水力相似原理

在水力學的研究中，從水流的內部機理直至與水流接觸的各種復雜邊界， 包括水力機械、水工建筑物等多方面的設計、施工及與運行管理等有關的水流問題，都可應用水力學模型實驗進行研究［3］。 即在一個與原型水流相似而縮小了幾何尺寸的模型中進行實驗。 如果在這種縮小了幾何尺寸的模型中，所有物理量都與原型相應點上對應物理量保持一定的比例關系，則這兩種流動現象就是相似的，這就是流動相似的基本涵義。

要保證油田實際管網與其等效的實驗管網流動相似，幾何相似、運動相似和動力相似是兩種管流系統保持相似的重要特性和基本條件［4］。而且這兩種系統相似是互相聯系、互為條件的。 3個相似是一個彼此密切相關的整體，缺一不可。

1.1 管網的變態水力模擬定義

目前， 管流正態相似的理論已相對較為成熟，但是在實驗過程中，由于受場地空間、制作條件和成本的限制，實際的管網模型難以搭建。 這時在建立管網模型時，就要考慮犧牲模型與原型的完全相似，而應用變態模型［5］。在變態模型中管網原型和等效管網模型之間的物理量關系通常用比尺來表征，比尺指的是原型和模型的物理量之比，一般用λ表示。 采用λL表示原型與管網模型之間的長度比尺， 用λd表示原型與管網模型的管徑比尺。 在管網變態模型的設計中，定義管長與管徑的比尺之比為變態率ζ（ζ=λL/λd）。 變態率是影響管網變態模擬的核心問題，會對研究結果產生很大的影響，其值一般不超過5［6］。

1.2 變態模擬力學相似準則

油田注水管網中作用于水流的力有很多，主要有重力、粘滯力及壓力等，這些力互不相同，各自遵遁不同的規律，并用不同形式的物理公式來表達［7］。 因此，要使實際管網與等效管網模型相似，不僅要考慮滿足牛頓相似定律，還要考慮這些力的影響。 然而，同時考慮幾種不同性質的力的相似有一定的困難。 在實際應用中，通常只考慮滿足一種或兩種決定水流流態的主要作用力的相似。 在油田注水管網中，管道水流承受的力主要來自壓力和粘滯力。

1.2.1 壓力相似準則

Eu為歐拉數，描述動量傳遞的特征數，在對油田管網水運動的研究分析中，一般采用壓差Δp進行分析，即：

1.3 管網的等效變態實驗模型構建推導

在壓力供水管網中，水流所承受的外力在液體內部的傳遞表現為內部的壓力［8］。變態模擬中，管網壓力相似即要求歐拉數相等，粘滯力的相似則表現為變態雷諾準數之間的關系。

首先由壓力相似準則（歐拉數相等）可以得到：

其中，λΔp、λρ、λv分別表示管網原型與等效管網模型的壓差比尺、密度比尺和流速比尺。

由粘滯力相似時雷諾數的關系，可得：

其中，λA、λV為管網原型與等效管網模型的截面積比尺和體積比尺。

經過以上一系列公式的推導，管網原型與等效的管網模型在滿足主要力相似準則的前提下，可以得到管網相似的基本比尺。 如果管材的粗糙系數比尺確定下來，管徑比尺、管長比尺和流速比尺根據需要選取，那么根據相似準則，整個管網模型的運行狀態也就可以確定下來。

1.4 運動相似條件的驗證

基于相似關系，管網原型與管網模型之間是否相似還需要運動相似比尺的吻合來檢驗［9］。 在實際管網中的液體質點和所建立等效管網模型中的質點沿著幾何相似的路徑，在互成一定比例的時間內通過幾何相似的路程。 油田注水實際管網與管網模型的運動相似的必要條件為：

驗證結果表明注水管網的原型與等效的管網模型滿足運動相似的必要條件。

通過壓力相似和粘滯力相似準則確定管網原型與等效的管網模型各個物理量的相似關系，得到管網原型與等效的管網模型變態幾何模型相似。 然后再通過運動相似準則的驗證，得出管網原型與管網模型流動相似。

2 單管線壓降實驗

在以上理論框架基礎上，為了實現采用高壓膠管構建油田注水管網的等效實驗管網，需要搭建高壓膠管單管線實驗裝置，對高壓膠管的沿程阻力損失和管材粗糙系數進行實驗分析。

實驗裝置如圖1所示，主要包括吸入管線、變頻離心泵、泵出管線、法蘭、壓力表、球閥、高精度壓力傳感器、電子流量計、高壓膠管、通孔閥塊、回水軟管及儲水罐等。 其中實驗的高壓膠管長度L=5000 mm，高壓膠管的內徑d=8 mm。 通過調節離心泵運行頻率改變離心泵的泵壓，記錄不同泵壓下高壓膠管的壓力損失情況，在高壓管線兩側分別放置壓力傳感器，實時監測高壓膠管的壓力損失情況。

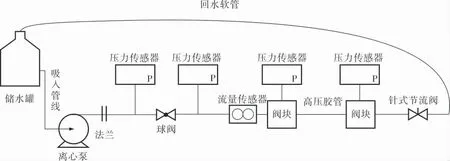
圖1 單管線壓降實驗模型

根據圖1所示，右閥塊記為節點1，左閥塊記為節點2。 在實地測量過程中，通過調整變頻離心泵的頻率，實時測量不同泵壓下兩節點的壓力和流量（表1）。

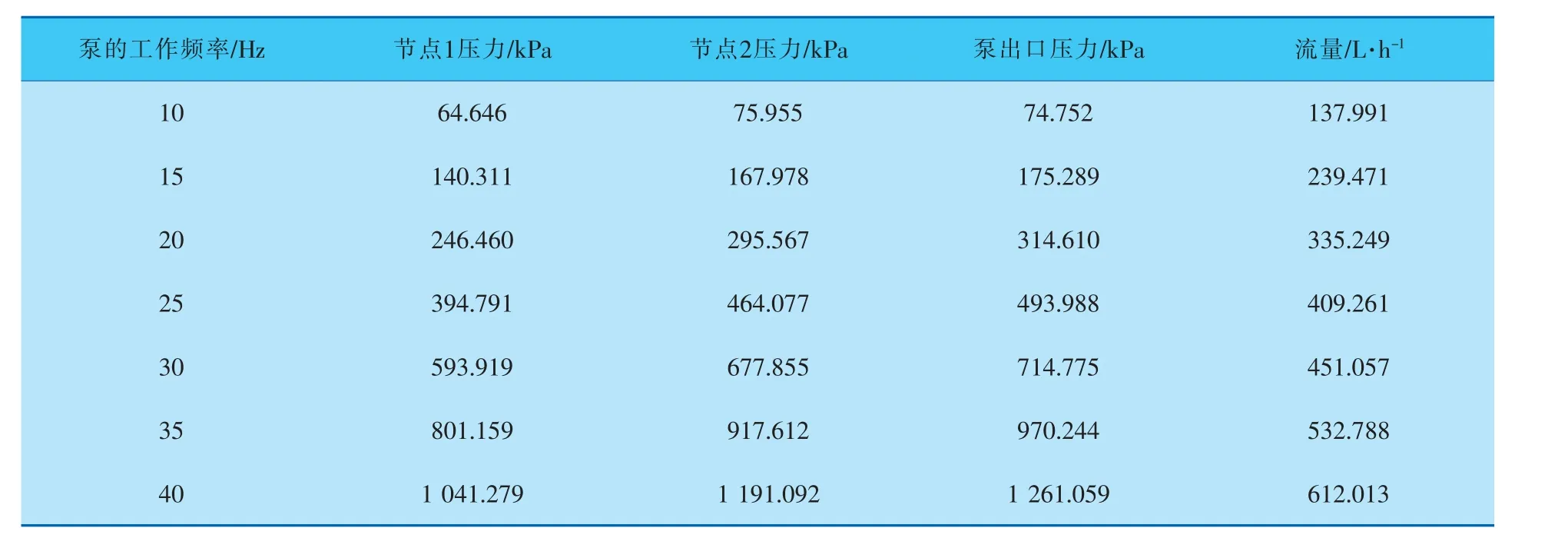
表1 不同工作頻率下兩節點的壓力和流量

當流體流經一定管徑的直管時，由于流體內的摩擦力而產生的阻力稱為沿程阻力；由阻力所產生的水頭損失稱為沿程水頭損失；當流體的固定邊界發生突然變化， 引起流速分布發生變化，從而集中發生在較短范圍的阻力稱為局部阻力［10］，局部阻力一般分布在接頭處。 在建立實驗管網時，由于進行了縮放變形，因此局部壓力損失往往不能忽略。 在實驗現場，兩節點間采用同一接頭、同一直徑，但盡可能短的高壓膠管管線進行實驗，保證準確地測定節點之間的局部阻力損失。 為此，采用L=50 mm的管段進行實驗，在不同管道流量下，測得局部阻力損失值。 通過表1可以看到在不同管道流量下節點壓力的實際測量值，從而可以得到兩個實測管道節點間的壓力損失值（表2）。

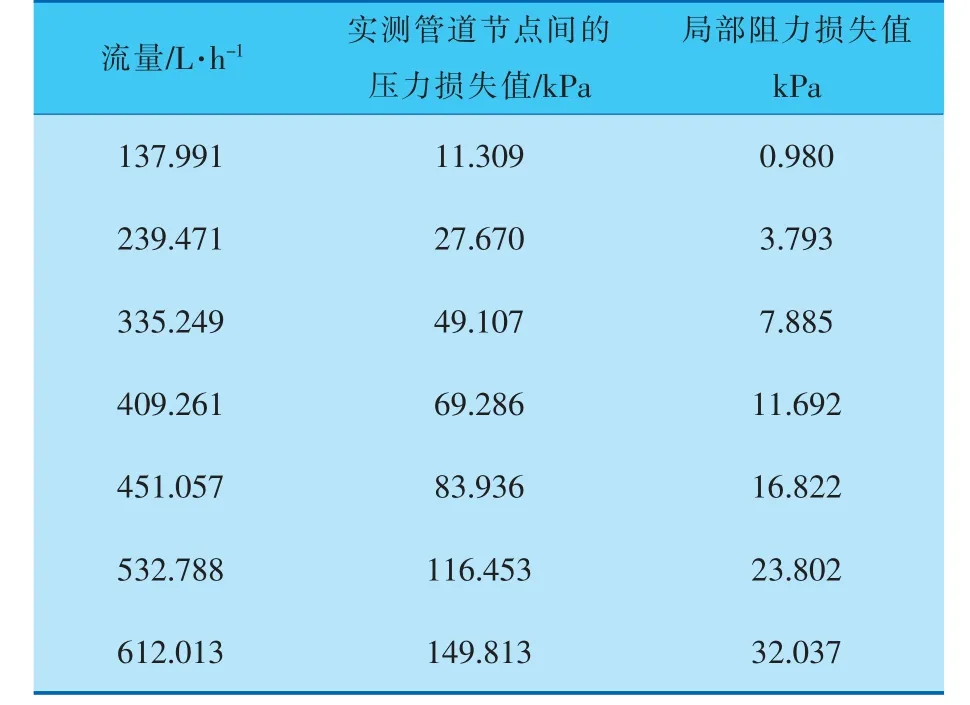
表2 不同管道流量下兩節點間的壓力損失和局部阻力損失值

3 高壓膠管的數據分析

筆者采用高壓膠管作為建立等效實驗管網的管線，通過單管線實驗測得的壓力損失數據與目前國內外使用較廣泛的海曾-威廉公式、 曼寧公式、 巴甫洛夫公式理論數據進行對比分析，得到與高壓膠管實驗數據相匹配的壓力損失公式和管材粗糙系數。

3.1 不同壓力損失公式下的沿程阻力損失分析

達西公式為均勻流沿程水頭損失的普遍計算式，對層流、紊流均適用，通用性比較強。 所以采用達西公式來計算流體沿程阻力損失，其表達式為：

式中 n——曼寧粗糙系數；

q——流量，m3/s。

海曾-威廉公式適用于較光滑的圓管滿管紊流計算，主要用于給水管道水力計算，公式為：

當n=0.013時，巴甫洛夫公式的壓力損失公式為：

已知高壓膠管的流量、 管徑及管長等數據，采用上述壓力損失公式對高壓膠管的壓力損失值進行計算。 將計算結果在MATLAB中通過調節各自壓力損失公式的管材粗糙系數進行修正，并利用最小二乘法對曲線進行一系列擬合。 得到最接近實際實驗數據趨勢的各個沿程阻力損失曲線（圖2）。

圖2 節點間壓力損失擬合

在不同的管道流量下，不同沿程阻力損失公式算得的壓力損失值見表3。

表3 不同管道流量下不同沿程阻力損失公式算得的壓力損失值

對于實際管網而言，局部損失與沿程損失往往比較小，有時可忽略或者適當調整一下管材粗糙系數來抵消管網運行中沿程阻力損失的影響。但在進行管網實驗時，由于管網模型一般都進行了縮小處理，因而局部阻力對整個管網的影響就顯得很大［11］。 所以在構建實驗室管網模型時，充分考慮這一點，對局部阻力進行了測定，對實驗結果進行處理和校正。

將測定的局部阻力損失與各個沿程阻力損失公式計算的理論值相加（局部阻力損失值見表2），可以得到各個沿程阻力損失公式計算的實際理論值（表4）。

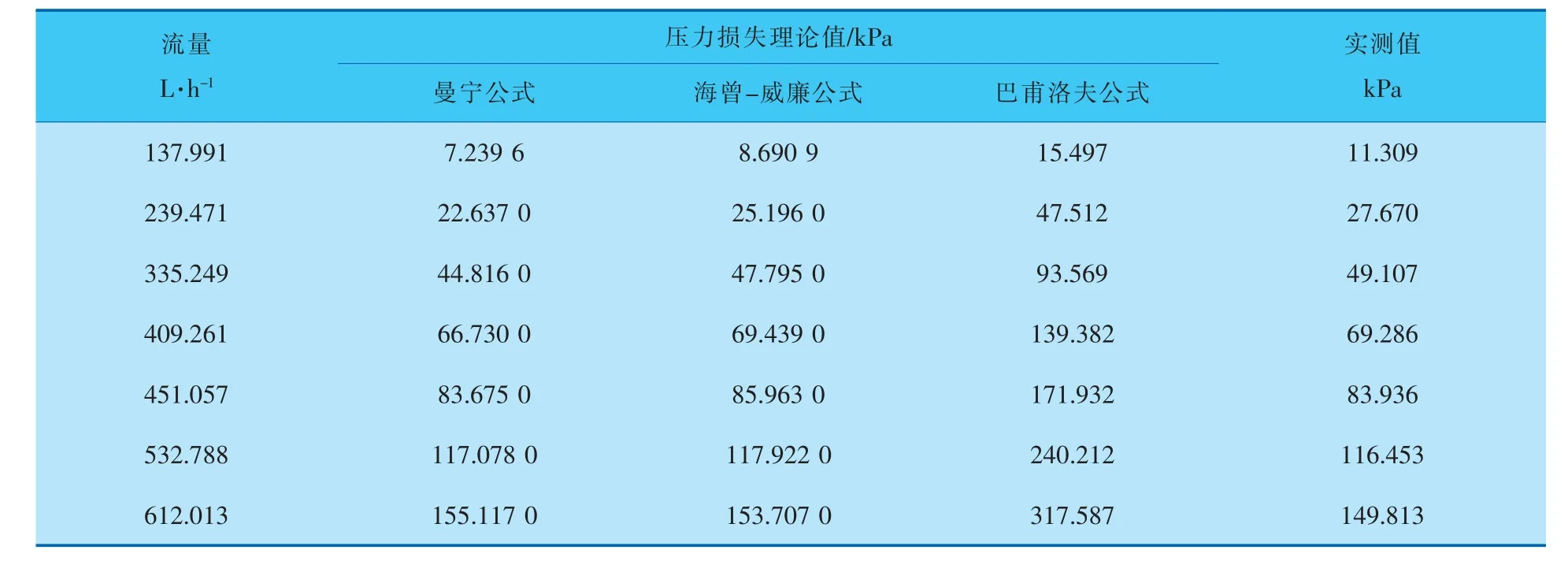
表4 壓力損失理論值與局部阻力損失疊加的準確壓力損失理論值

基于表4中的數據， 對不同沿程阻力損失公式下的壓力損失和實際測量實驗數據利用MATLAB重新擬合，結果如圖3所示。

圖3 考慮局部阻力的壓力損失擬合

通過對高壓膠管的單管線壓降實驗數據分析可以看到： 海曾-威廉公式和曼寧公式計算的沿程阻力損失數據曲線與實驗測試數據曲線基本吻合，而巴甫洛夫公式的計算數據曲線與實驗測試數據曲線相差較大。 說明海曾-威廉公式和曼寧公式適用于高壓膠管的沿程阻力損失計算，而巴甫洛夫公式因誤差較大相比不適合高壓膠管的沿程阻力損失計算。

3.2 管材粗糙系數的求解

對適用于高壓膠管沿程阻力損失計算的海曾-威廉和曼寧公式粗糙系數進行計算， 在實地測量中，已知L=5000 mm，d=8 mm，由于在同一種壓力損失計算公式中高壓膠管的管材粗糙系數都是相同的，因此取當流量q=137.991 L/h，海曾-威廉公式壓力損失Δp=7.7109 kPa時的情況。由式（20）可得：

當流量q=137.991 L/h， 曼寧公式壓力損失Δp=6.2596 kPa時，計算得高壓膠管的曼寧粗糙系數n=0.0075。

通過對海曾-威廉公式和曼寧公式計算的沿程阻力損失數據反向求解得到了高壓膠管的海曾-威廉粗糙系數和曼寧粗糙系數。

4 結束語

筆者根據變態相似理論，建立油田注水管網系統與等效的實驗管網模型之間的理論框架，即壓力和粘滯力作為注水管網的主要作用力，且滿足壓力變態準則和阻力相似準則的條件下，推導出管材的粗糙系數作為等效實驗管網模型與注水管網原型主要相似關系比尺之一。 通過對實驗平臺的搭建， 對高壓膠管的壓力損失進行測量。之后將不同的沿程阻力損失公式對高壓膠管進行壓力損失計算并疊加局部阻力損失， 采用MATLAB軟件對實驗數據擬合分析后， 確定高壓膠管適合的沿程阻力損失計算公式，最后經過確定公式的反演， 得到高壓膠管的海曾-威廉粗糙系數和曼寧粗糙系數。 根據求得的高壓膠管粗糙系數，則可以使等效物理實驗模型和管網原型的粗糙系數比尺確定下來，使管網的相似關系進一步完善。 以上工作為進一步研究油田注水管網運行提供了支持，為建立與油田注水管網等效的實驗管網奠定了基礎。