基于多目標的刨切機床身結構優化設計

任 旺，劉芳華，仲昭杰，郭文龍，吳萬毅

(江蘇科技大學機械工程學院，江蘇 鎮江 212100)

0 引言

床身作為刨切機重要的基礎支撐部件，其動靜態特性直接影響著整機的加工精度、穩定性和可靠性[1]。為保證刨切機能滿足高精度、高效、穩定的工作要求，對床身進行合理的結構優化設計以提高其力學性能尤為重要。

傳統刨切機床一般依靠經驗進行結構設計，由于設計理論基礎的不足，為了保證機床工作性能，設計參數會比實際需要的更大一些，就會造成重量大、耗材高等問題，而且往往結構上也難以實現最優化。隨著有限元分析技術和新優化算法的發展，結構優化設計效率大大提高。目前，國內外學者普遍采用尺寸優化的方法應用于機床的結構設計與優化中。鄭彬等[2]通過模態分析確定某銑床床身的薄弱處，對其主要尺寸進行試驗設計、靈敏度分析并建立響應面模型，利用多目標優化算法對其結構優化；甘盛霖等[3]針對某磨床床身，通過靈敏度分析確定影響床身靜動態特性和整體質量的主要參數，對床身內部筋板厚度和布局方式進行尺寸優化，得到了最佳結構優化方案；楊志賢等[4]通過正交實驗法建立了響應面模型，采用遺傳算法對其多目標優化求解，并基于信息熵賦權的多目標灰靶決策算法進行解集優選；劉峰等[5]采用實驗模態測試確定出某機床的工作臺為薄弱環節，將靈敏參數作為設計變量，以低階固有頻率、質量和剛度為優化目標進行尺寸優化；薛會民等[6]利用尺寸優化和拓撲優化方法，對床身進行以減輕質量和提高剛度為目標的結構優化。

本文以某數控刨切機床身為研究對象，進行靜力學分析和模態分析，以床身質量、最大靜變形和一階固有頻率為優化目標，對設計參數進行靈敏度分析并建立響應面模型，采用遺傳算法對床身主要設計參數進行多目標優化，為提高床身性能打下基礎。

1 床身靜動態特性分析

1.1 床身靜力學分析

床身內部采用布置筋板的結構方式，其中床身前端有2塊主筋板和4塊副筋板，床身后端內部有6塊橫向筋板，底部的支撐面由6個地腳螺栓進行固定，床身上部的螺紋孔用于安裝固定工作臺、刀架等其他零部件。

床身采用的材料為灰鑄鐵HT250，其材料屬性:密度為7 200 kg/m3，彈性模量為110 GPa，泊松比為0.28[7]。為方便網格劃分，提高運算效率，有必要對床身模型上的螺紋孔、圓角、倒角以及凸臺等對分析結果影響較小的特征進行簡化或忽略，再將簡化后的模型導入到ANSYS Workbench中進行網格劃分，采用四面體單元對床身進行網格劃分。

在進行靜力學分析時，床身上受到的載荷主要為自身的重力和安裝在床身上的工作臺等其他零部件的質量，床身底部通過螺栓進行固定約束。經計算求解，得到靜力學分析結果如圖1所示。

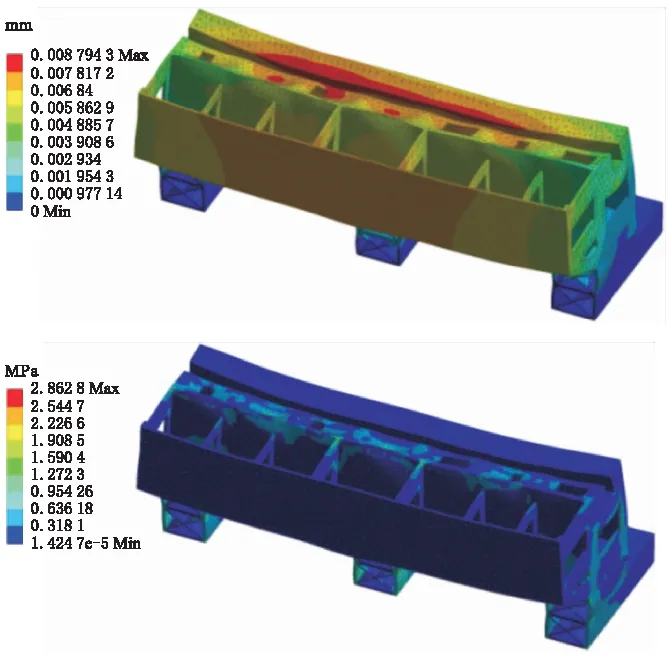
圖1 靜力學分析結果

由圖1可知，最大變形位于床身上部與安裝其他部件的連接處，變形量最大為8.794 3 μm，最大應力位于床身底座連接處以及內部各筋板接觸部位，最大應力為2.862 8 MPa，遠小于材料的強度極限，可知床身設計有較大的余量，對床身結構需要進一步優化，以提高其動靜態性能。

1.2 模態分析

在對床身模態分析時，不需要考慮施加任何載荷，只需對床身底部螺栓進行固定約束。機床在工作過程中，當在外部激振頻率接近床身固有頻率，會產生共振現象，對機床加工的精度和穩定性有重要影響，應避免接近振動頻率范圍。低階模態是影響機床動態性能的主要因素，因此提取床身的前4階模態進行分析，其前2階振型如圖2所示，前4階振型和固有頻率如表1所示。

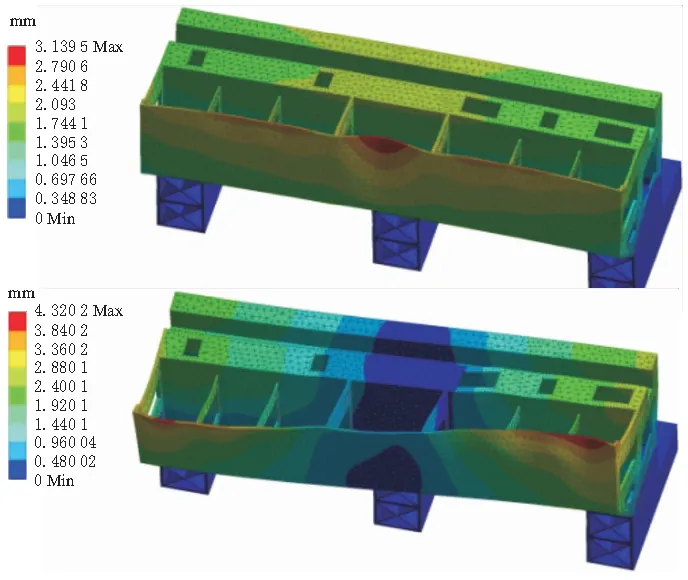
圖2 床身前2階振型

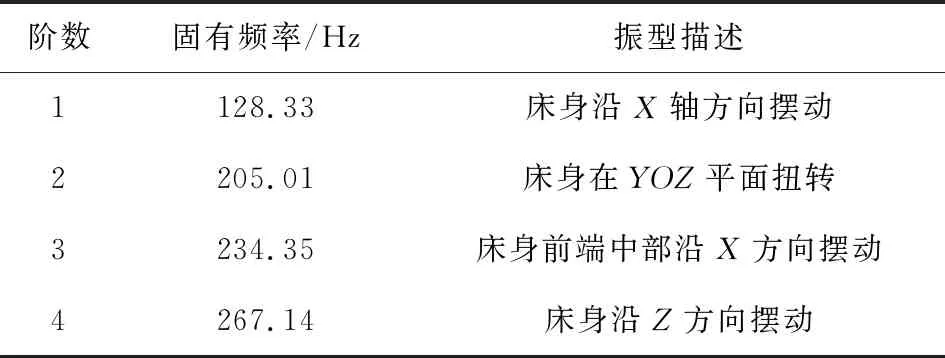
表1 床身前4階固有頻率和振型

2 響應面模型的建立

2.1 設計變量的選擇

床身尺寸參數較多，不可能選取每個參數進行優化。為此需要考慮影響床身性能較大的參數，將床身前后端外部壁厚、前后端內部筋板厚度等5個參數作為設計變量，如圖3所示。

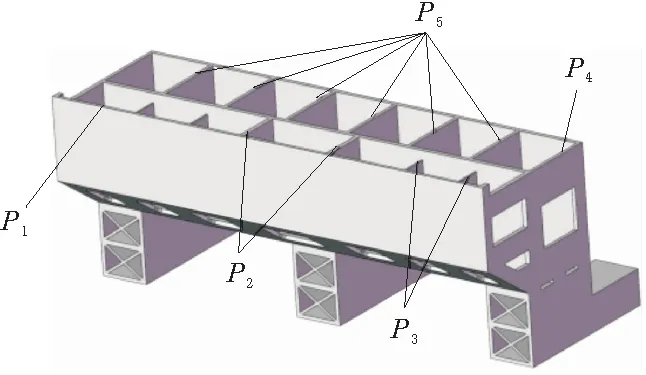
圖3 床身設計參數

在床身原有結構不變的基礎上，確定設計變量參數的取值范圍，參數及變化范圍如表2所示。

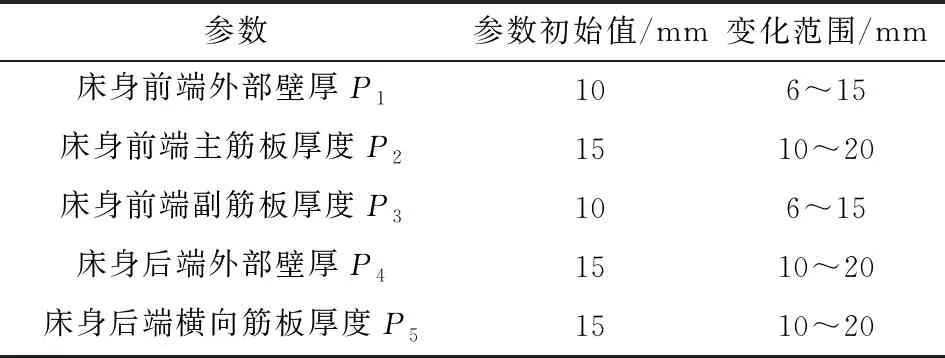
表2 設計變量及參數變化范圍

2.2 DOE試驗設計

在ANSYS Workbench的Design of Experiment模塊中對床身進行拉丁超立方試驗設計，系統自動生成27組樣本數，以床身質量P6、靜態最大變形量P7和一階固有頻率P8為輸出參數，部分樣本點及試驗結果如表3所示。

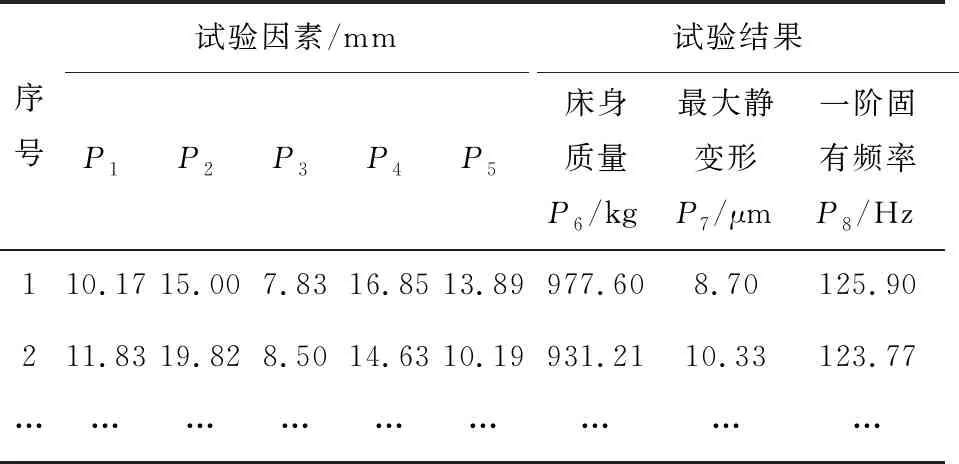
表3 部分樣本點及試驗結果

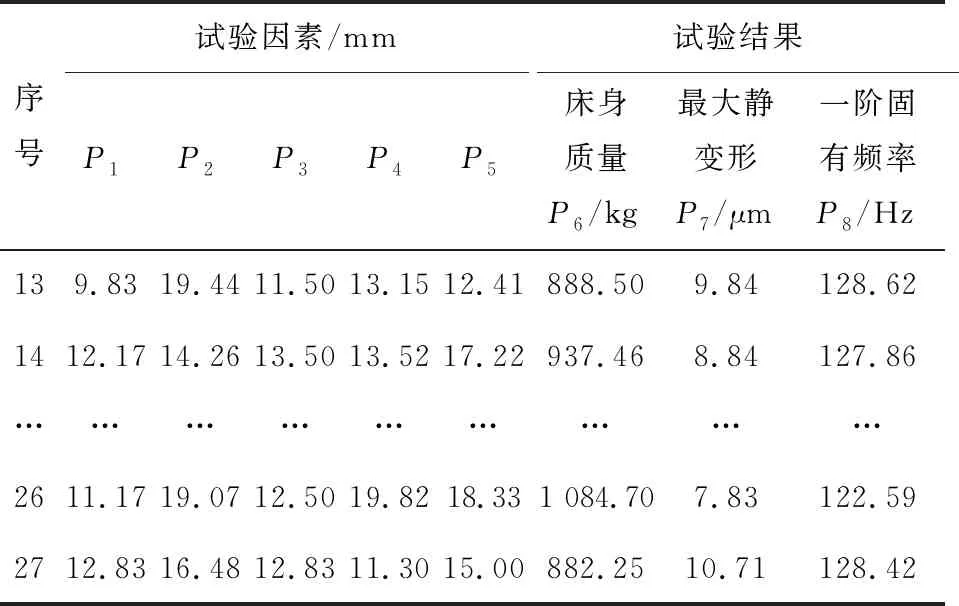
表3(續)

2.3 響應面分析

響應面法是結合數理統計原理，通過試驗設計對指定樣本點集合進行試驗分析，得到設計變量的目標函數與約束函數的響應面模型，來預測非試驗點的響應值[8]。本文選用二階響應面模型，即

(1)

Y(X)為輸出變量；X為設計變量；n為設計變量的個數；α0、αi、αij為未知系數，由最小二乘法求解確定。

為評價響應面模型質量，利用參數R2來評估響應面擬合精度，當R2接近1時，表明響應面擬合精度較高[9]。

(2)

(3)

(4)

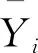
圖4～圖6分別為設計變量P1、P4與質量的響應面、設計變量P4、P5與最大靜變形的響應面、設計變量P1、P4與一階固有頻率的響應面。

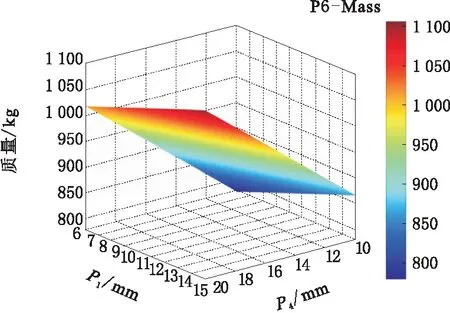
圖4 設計變量P1、P4與質量的響應面

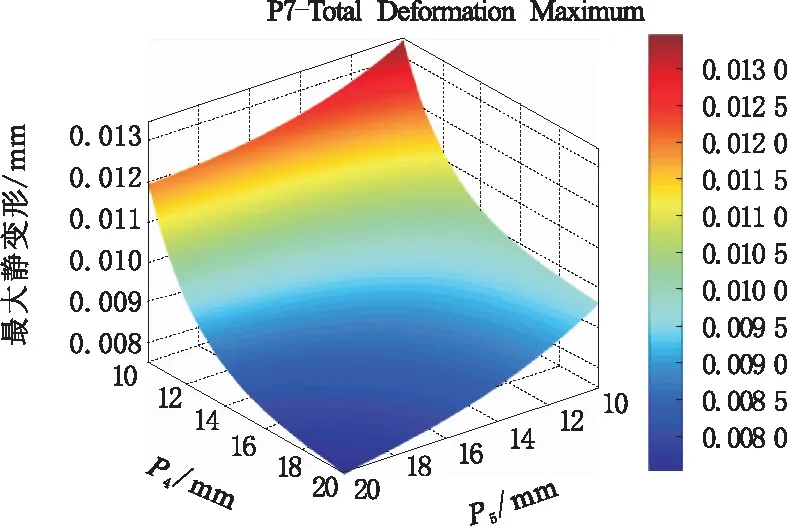
圖5 設計變量P4、P5與變形量的響應面

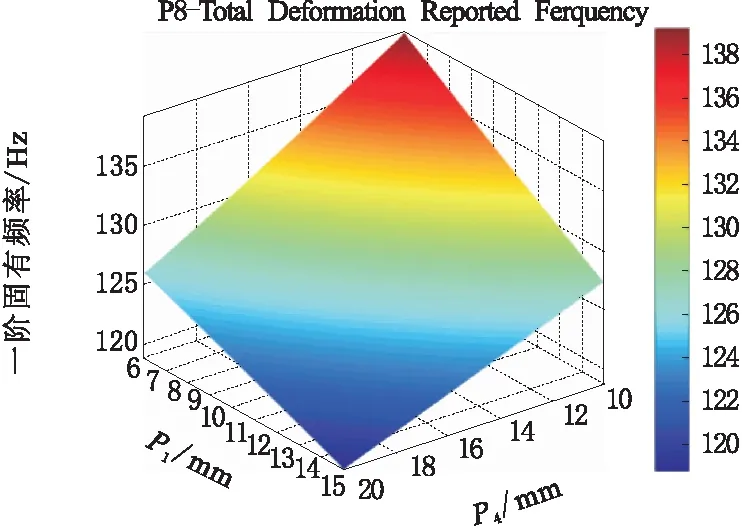
圖6 設計變量P1、P4與一階固有頻率的響應面

由圖4可知，隨著床身前后端外部壁厚P1、P4的增大，質量也隨之增大；由圖5可知，隨著床身后端外部壁厚P4和橫向筋板厚度P5的增大，最大靜變形迅速減小；由圖6可知，當床身前后端外部壁厚P1、P4在最大值時，一階固有頻率最小。根據響應面圖分析可知各個設計變量對輸出參數的影響，在為后續設計變量優化時，需綜合考慮設計變量對床身結構性能的影響程度，選擇合理的設計方法，以尋求最佳參數組合，使其性能達到最優。

2.4 靈敏度分析

在進行結構優化時，床身結構性能(輸出參數)一般由多個設計變量相互作用決定的，經由靈敏度分析可以確定設計變量對輸出參數的影響程度，選取對輸出參數影響顯著的設計變量作為關鍵變量進行優化設計。經分析得到各設計變量對輸出參數的靈敏度，如表4所示。

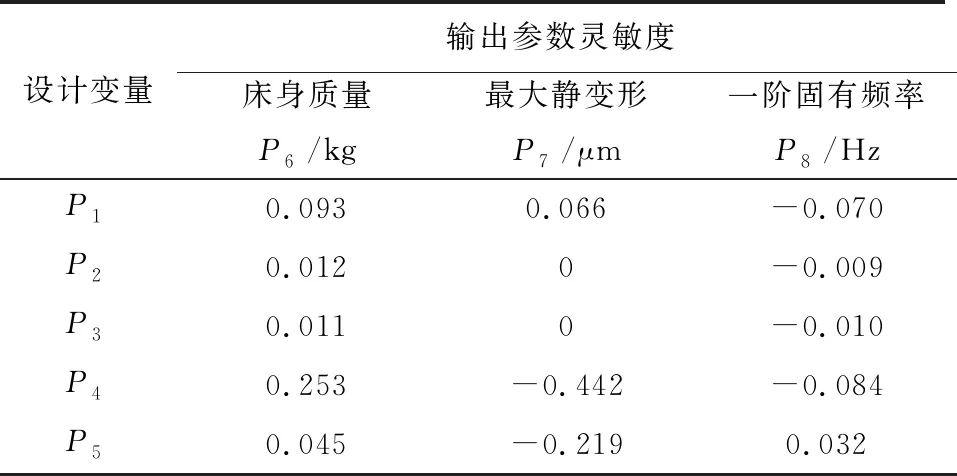
表4 各設計變量對輸出參數的靈敏度

在進行靈敏度分析時，當設計變量為正值時，設計變量對輸出參數成正相關；當設計變量為負值時，設計變量對輸出參數成負相關。由表4可知，床身后端外部壁厚對床身質量影響最大，其余設計變量影響較小；床身后端壁厚和內部橫向筋板厚度對最大靜變形影響較大且成負相關，主要由于最大靜變形集中在床身上部；只有內部橫向筋板厚度對一階固有頻率成正相關，其余設計變量對其成負相關，床身前后端壁厚對其影響較大，主要原因是一階振型為床身橫向擺動。

3 床身多目標優化

3.1 床身多目標優化數學模型

以床身質量、最大靜變形和一階固有頻率為優化目標，選取好設計變量參數，設定其參數變化范圍，建立多目標優化數學模型，可表示為：

min[m(X),fd(X),-ff(X)]

X=[x1,x2,x3,x4,x5]T

s.t.xim≤xi≤xin，i=1,2,…,5

m(X)為床身質量；fd(X)為最大靜變形；ff(X)為一階固有頻率；x為設計變量；xim、xin分別為各設計變量的上限值和下限值。

3.2 基于遺傳算法的多目標優化

采用多目標遺傳算法(MOGA)[10]對優化目標進行優化求解。以床身質量最小、最大靜變形最小和一階固有頻率最大為優化目標，進行多目遺傳算法的優化求解，經求解得到一系列Pareto最優解。在Pareto解集中選出的3組最佳優化解，如表5所示。

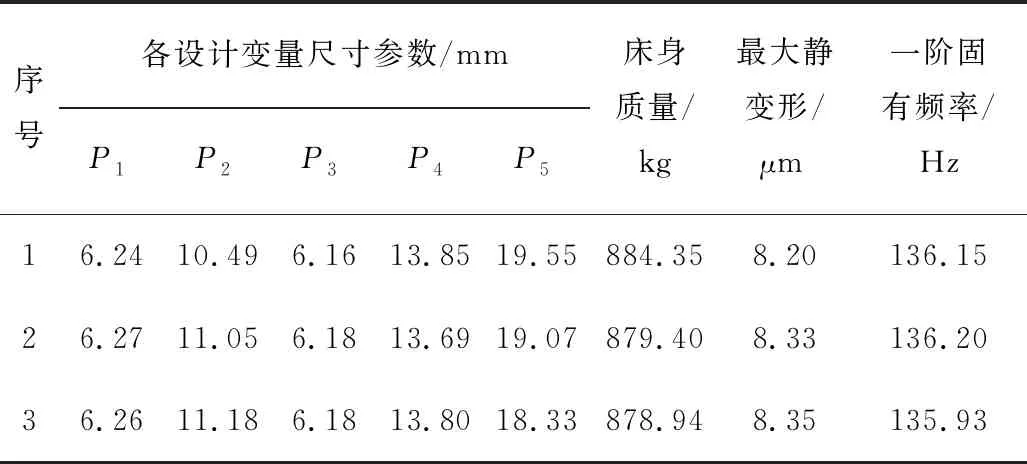
表5 最佳優化解集

3.3 多目標優化結果分析

根據對設計目標的要求，經過對比分析，從中選擇1組效果較優的參數作為優化結果，對參數進行圓整，優化前后設計變量的參數對比結果如表6所示。

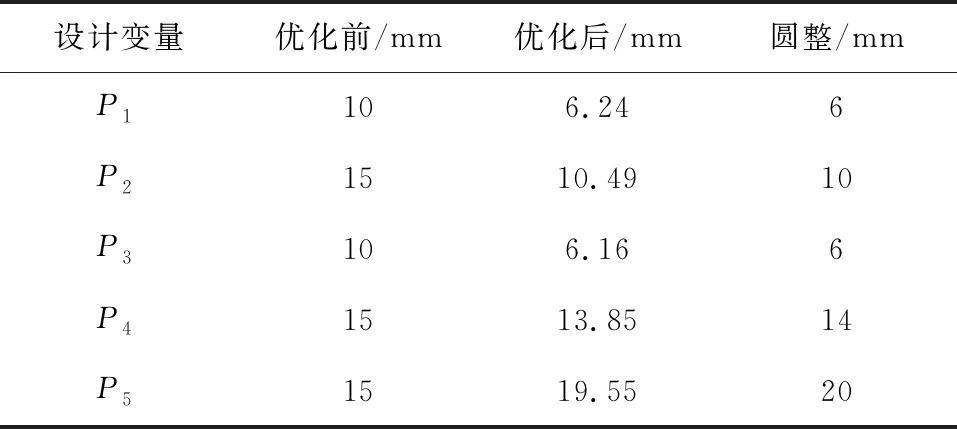
表6 優化前后參數對比

對優化后的床身進行動靜態特性分析，優化前后的結果對比如表7所示。

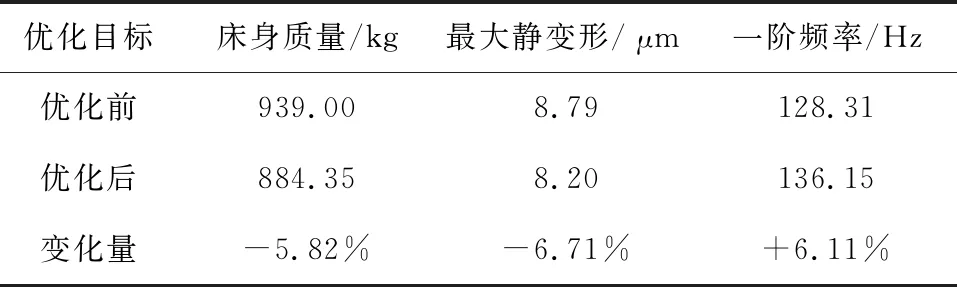
表7 優化前后結果對比

由表7可知，床身質量減少了54.65 kg，優化后的床身質量減幅為5.82%；優化前的最大靜變形為8.79 μm，經優化后最大靜變形為8.20 μm，減幅為6.71%；一階固有頻率提升了6.11%。在床身質量減輕的基礎上，床身的最大靜變形和一階固有頻率均得到明顯優化。

4 結束語

本文以某刨切機床身為研究對象，提出一種基于靈敏度分析的多目標優化設計方法。對床身進行有限元分析，找出床身的薄弱部位；針對床身外部壁厚、內部各筋板厚度進行拉丁超立方試驗設計，通過靈敏度分析并建立響應面模型，確定了各設計變量對床身質量和床身動靜態特性的影響程度；以降低床身最大靜變形和質量，提高一階固有頻率為優化目標，采用多目標遺傳算法對床身進行優化并得到最佳優化解集。在減輕床身質量的同時，提高了床身結構性能。該設計方法為床身的優化設計和改造效率的提升提供一定理論依據。