基于統(tǒng)一強(qiáng)度理論的非靜水壓圓形隧道塑性區(qū)半徑的脆塑性攝動(dòng)解1)

張常光 李宗輝 關(guān)港輝 孫 松

* (長安大學(xué)建筑工程學(xué)院,西安 710061)

? (地質(zhì)災(zāi)害防治與地質(zhì)環(huán)境保護(hù)國家重點(diǎn)實(shí)驗(yàn)室,成都 610059)

引言

隧道工程在國家重大基礎(chǔ)設(shè)施投資中的份額高,針對(duì)復(fù)雜地質(zhì)環(huán)境的隧道彈塑性分析及支護(hù)設(shè)計(jì)具有重要工程應(yīng)用價(jià)值,其中常用側(cè)壓力系數(shù)表示水平地應(yīng)力與豎向地應(yīng)力存在明顯差異的非靜水壓力為隧道所處真實(shí)地應(yīng)力場的鮮明特征,靜水壓力下隧道的計(jì)算理論不再適用.目前,基于Mohr-Coulomb 強(qiáng)度準(zhǔn)則和理想彈塑性模型,眾多學(xué)者采用Kastner 法[1-7]、復(fù)變函數(shù)法[8-12]、總荷載不變法[13-15](彈-脆-塑性模型)、數(shù)值模擬[16]和攝動(dòng)法[17-18],探討了非靜水壓力下圓形隧道的非圓塑性區(qū)邊界線.

Kastner[1]將非靜水壓力下圓形隧道處于純彈性狀態(tài)時(shí)應(yīng)力的基爾希公式代入Mohr-Coulomb 強(qiáng)度準(zhǔn)則以確定隧道的非圓塑性區(qū)邊界線.王衛(wèi)軍等[2-3]和郭曉菲等[4]基于Kastner 法提出隧道的蝶形塑性區(qū)概念,Yuan 等[5]和Zou 等[6]將基爾希公式代入統(tǒng)一強(qiáng)度理論建立了隧道非圓塑性區(qū)的邊界線方程,于學(xué)馥等[7]考慮塑性應(yīng)力重分布修正了Kastner法.值得注意的是,Kastner 法忽略了圍巖的彈塑性發(fā)展過程,近似地將純彈性狀態(tài)下基爾希公式直接代入圍巖強(qiáng)度準(zhǔn)則,但非靜水壓力下隧道的塑性區(qū)邊界線不是圓形.

Wang 等[8]、Yan 等[9]和呂愛鐘等[10-12]采用復(fù)變函數(shù)法將非圓形的隧道塑性區(qū)邊界線保角映射為圓形求解,邏輯上合理但分析過程和公式都較為復(fù)雜.嚴(yán)克強(qiáng)[13]、董海龍等[14-15]由總荷載不變法推導(dǎo)了隧道水平或豎向的塑性區(qū)半徑,而其他方位處的需由相似原理給出.Bagheri 等[16]通過二維彈塑性有限元數(shù)值模擬獲得了隧道的非圓塑性區(qū),但與模型邊界、網(wǎng)格尺寸等密切相關(guān).魏悅廣[17]和Tang 等[18]基于攝動(dòng)法將隧道非圓塑性區(qū)邊界和彈性區(qū)應(yīng)力求解轉(zhuǎn)化為數(shù)學(xué)微分方程,計(jì)算精度高、誤差小.此外,Kabwe 等[19]采用Drucker-Prager 強(qiáng)度準(zhǔn)則對(duì)非圓形隧道進(jìn)行了理想彈塑性分析.

巖石真三軸試驗(yàn)表明[20-23]:中間主應(yīng)力對(duì)巖石強(qiáng)度的提高作用明顯,Mohr-Coulomb 強(qiáng)度準(zhǔn)則未考慮中間主應(yīng)力而低估了巖石強(qiáng)度,統(tǒng)一強(qiáng)度理論[24]合理考慮了巖土材料強(qiáng)度的中間主應(yīng)力效應(yīng).同時(shí),巖石峰后強(qiáng)度相比峰前常有較大跌落,彈-脆-塑性模型較理想彈塑性模型可描述脆性軟化后巖石的強(qiáng)度變化[25-26],上述研究中只有文獻(xiàn)[14-15]使用了彈-脆-塑性模型.因此,本文基于統(tǒng)一強(qiáng)度理論和彈-脆-塑性模型,考慮中間主應(yīng)力效應(yīng)和脆性軟化的共同影響,從側(cè)壓力系數(shù)小于1 出發(fā),采用攝動(dòng)法建立非靜水壓圓形隧道塑性區(qū)半徑的解析解,給出所得解析解的適用范圍,并與文獻(xiàn)復(fù)變函數(shù)法、攝動(dòng)法、數(shù)值模擬和總荷載不變法進(jìn)行對(duì)比驗(yàn)證,最后探討攝動(dòng)參數(shù)、中間主應(yīng)力和脆性軟化對(duì)隧道塑性區(qū)形狀與大小的影響規(guī)律.

1 基本理論

隧道開挖可簡化為平面應(yīng)變問題,遵循先加載后成洞規(guī)律.圖1 為非靜水壓力下圓形隧道的平面應(yīng)變力學(xué)模型,支護(hù)力pi均勻地作用在隧道洞壁處,無窮遠(yuǎn)處作用豎向地應(yīng)力q.

圖1 非靜水壓力下圓形隧道的力學(xué)模型Fig.1 Mechanical model of a circular tunnel under non-hydrostatic pressures

在圖1 中,a為隧道半徑,Rp為塑性區(qū)半徑;r,θ分別為極坐標(biāo)的半徑和方位角,且θ以水平向右方向?yàn)槠瘘c(diǎn)、逆時(shí)針旋轉(zhuǎn)為正;ε為攝動(dòng)參數(shù),側(cè)壓力系數(shù)λ=1 -ε,本文將從側(cè)壓力系數(shù)λ小于1 即0＜ε=1-λ＜1 出發(fā),規(guī)定以壓應(yīng)力為正,并將無窮遠(yuǎn)處的水平/豎向地應(yīng)力轉(zhuǎn)換為徑向/切向地應(yīng)力,以采用極坐標(biāo)求解非靜水壓力圓形隧道問題.

1.1 彈-脆-塑性模型和統(tǒng)一強(qiáng)度理論

巖土類材料的彈-脆-塑性模型如圖2(a)所示[26],圖中σ1為大主應(yīng)力、σ3為小主應(yīng)力,ε1為大主應(yīng)變.彈-脆-塑性模型考慮了圍巖峰后強(qiáng)度相比峰前有較大損失的脆性軟化,較理想彈塑性模型更適合描述圍巖峰后強(qiáng)度的真實(shí)變化.統(tǒng)一強(qiáng)度理論的 π 平面極限線如圖2(b)所示[24],不同的統(tǒng)一強(qiáng)度理論參數(shù)b對(duì)應(yīng)Mohr-Coulomb 強(qiáng)度準(zhǔn)則(b=0)、雙剪應(yīng)力強(qiáng)度準(zhǔn)則(b=1)以及一系列強(qiáng)度準(zhǔn)則(0＜b＜1),以反映中間主應(yīng)力σ2的不同影響程度.

圖2 彈-脆-塑性模型和統(tǒng)一強(qiáng)度理論Fig.2 Elastic-brittle-plastic model and unified strength theory

采用黏聚力c和內(nèi)摩擦角φ作為巖土材料強(qiáng)度參數(shù)時(shí),以壓應(yīng)力為正的統(tǒng)一強(qiáng)度理論表達(dá)式為[27]

對(duì)于圓形隧道開挖平面應(yīng)變問題,假設(shè)隧道縱向應(yīng)力σz為中間主應(yīng)力σ2且主應(yīng)力之間的關(guān)系為[6,27-28]

因此,式(2)滿足式(1b)的應(yīng)力判定條件.將式(2)代入式(1b),整理得統(tǒng)一強(qiáng)度理論的平面應(yīng)變表達(dá)式為

假設(shè)圍巖為均勻、連續(xù)且各向同性的彈-脆-塑性材料,屈服時(shí)遵循統(tǒng)一強(qiáng)度理論,則由式(3)得隧道圍巖峰前/峰后的強(qiáng)度準(zhǔn)則為[28]

式(6)表示圍巖主應(yīng)力與極坐標(biāo)應(yīng)力分量之間的關(guān)系,其中σr,σθ,τrθ分別為非靜水壓力下圍巖的徑向正應(yīng)力、切向正應(yīng)力和切應(yīng)力

將式(6)分別代入式(4)和式(5),得非靜水壓力下隧道圍巖峰前/峰后的強(qiáng)度準(zhǔn)則為

1.2 攝動(dòng)法

對(duì)于非靜水壓力下圓形隧道的彈塑性非圓邊界問題,攝動(dòng)法將彈塑性非圓邊界轉(zhuǎn)化為數(shù)學(xué)微分方程,再根據(jù)無窮遠(yuǎn)處的應(yīng)力邊界逐階求解.由應(yīng)力坐標(biāo)轉(zhuǎn)換公式得無窮遠(yuǎn)處(+r面)的徑向正應(yīng)力σr|r→∞和切應(yīng)力τrθ|r→∞為

圖3 為攝動(dòng)法求解非靜水壓力下圓形隧道塑性區(qū)半徑的逐階過程,洞壁處始終作用均勻支護(hù)力pi,無窮遠(yuǎn)處應(yīng)力邊界按攝動(dòng)參數(shù)ε的階數(shù)進(jìn)行離散.首先求作用下即ε0階問題的圍巖彈性區(qū)應(yīng)力和隧道塑性區(qū)半徑,后續(xù)每個(gè)離散的應(yīng)力邊界在前一階解答的基礎(chǔ)上逐階修正,最終獲得εn階問題的解答.

Φ是關(guān)于半徑r和方位角θ的應(yīng)力函數(shù),式(10)為應(yīng)力函數(shù)Φ(r,θ)需滿足的相容方程

圍巖彈性區(qū)應(yīng)力可由應(yīng)力函數(shù)Φ(r,θ)表示為

由圖3 可知,圍巖彈性區(qū)應(yīng)力、隧道塑性區(qū)半徑和應(yīng)力函數(shù)均與無窮遠(yuǎn)處的應(yīng)力邊界有關(guān),將這些量按攝動(dòng)參數(shù)ε的階數(shù)展開得其攝動(dòng)解形式為

圖3 攝動(dòng)法逐階求解Fig.3 Steps to apply the perturbation method

聯(lián)立式(9)、式(12a)和式(12c),依據(jù)攝動(dòng)參數(shù)ε各次項(xiàng)的系數(shù)相等得隧道無窮遠(yuǎn)處的應(yīng)力邊界為

式(13)為攝動(dòng)法求解非靜水壓力下圓形隧道塑性區(qū)半徑Rp的表達(dá)式,可結(jié)合定解條件依次獲得ε0階塑性區(qū)半徑R0,ε1階塑性區(qū)半徑R0[1-εR1(θ)](求R1(θ)),ε2階塑性區(qū)半徑R0[1-εR1(θ)-ε2R2(θ)](求R2(θ)),持續(xù)計(jì)算εn階的塑性區(qū)半徑(求Rn(θ),n≥3),相鄰階數(shù)間的結(jié)果相差滿足精度時(shí)停止計(jì)算.

2 塑性區(qū)半徑求解

2.1 塑性區(qū)應(yīng)力

在非靜水壓力下圓形隧道的圍巖塑性區(qū)內(nèi),平衡微分方程為

當(dāng)塑性區(qū)完全包圍隧道時(shí),圍巖塑性區(qū)應(yīng)力只與隧道洞壁處的應(yīng)力邊界和幾何形狀有關(guān)[10-12,14-15,17-18],屬于屈服方程和平衡微分方程聯(lián)立求解的靜定邊值問題,且在圍巖塑性區(qū)內(nèi)σr＜σθ.由圖1 可知,圓形隧道在r=a處σr=pi,τrθ=0,表明洞壁處的應(yīng)力邊界和幾何形狀均為繞軸對(duì)稱,根據(jù)連續(xù)性條件得圍巖塑性區(qū)的應(yīng)力與方位角θ無關(guān),其徑向正應(yīng)力σr和切向正應(yīng)力σθ只與半徑r有關(guān),又因切應(yīng)力τθr關(guān)于θ面反對(duì)稱,則切應(yīng)力τrθ(p)=τθr(p)≡0,進(jìn)而在圍巖塑性區(qū)內(nèi)式(16b)恒成立,式(16a)變?yōu)?/p>

聯(lián)立圍巖峰后強(qiáng)度準(zhǔn)則式(8)和平衡微分方程式(17),并結(jié)合τrθ(p)≡0 和隧道洞壁處的應(yīng)力邊界即定解條件r=a時(shí)σr=pi,得圍巖塑性區(qū)應(yīng)力為

式中,上標(biāo)p 代表圍巖塑性區(qū)、彈塑性交界線內(nèi)側(cè).

對(duì)于彈-脆-塑性模型下隧道彈塑性交界線的內(nèi)側(cè)與外側(cè),圍巖存在強(qiáng)度突變,塑性應(yīng)力也產(chǎn)生了突變:彈塑性交界線的內(nèi)側(cè)屬于塑性區(qū),應(yīng)力滿足以圍巖殘余強(qiáng)度參數(shù)表達(dá)的峰后強(qiáng)度準(zhǔn)則式(8),可令式(18)中r=Rp獲得;彈塑性交界線的外側(cè)屬于塑性區(qū)也屬于彈性區(qū),應(yīng)力滿足以圍巖初始強(qiáng)度參數(shù)表達(dá)的峰前強(qiáng)度準(zhǔn)則式(7),聯(lián)立式(7)、式(17)和沿著彈塑性交界線的法線方向應(yīng)力連續(xù)、切線方向應(yīng)力連續(xù)得外側(cè)三個(gè)塑性應(yīng)力分量為

式中,上標(biāo)op 代表彈塑性交界線外側(cè).

因此,彈塑性交界線內(nèi)側(cè)與外側(cè)上每點(diǎn)都處于繞軸對(duì)稱的主應(yīng)力狀態(tài),徑向正應(yīng)力、切向正應(yīng)力可分別類比為巖石軸對(duì)稱三軸壓縮試驗(yàn)的圍壓和抗壓強(qiáng)度,圍壓相同但抗壓強(qiáng)度不同,進(jìn)而在彈塑性交界線內(nèi)側(cè)與外側(cè)的兩個(gè)塑性應(yīng)力分量連續(xù)(徑向正應(yīng)力、切應(yīng)力),而切向塑性應(yīng)力發(fā)生了突變.但在彈塑性交界線的外側(cè),三個(gè)應(yīng)力分量的塑性值與彈性值均相等,將作為2.2 節(jié)中塑性區(qū)半徑計(jì)算的定解條件之一.

2.2 塑性區(qū)半徑

非靜水壓力下圓形隧道彈性區(qū)應(yīng)力滿足兩個(gè)位置的應(yīng)力邊界,一是無窮遠(yuǎn)處,徑向正應(yīng)力與切應(yīng)力收斂于式(15),二是彈塑性交界線的外側(cè),三個(gè)應(yīng)力分量的塑性值與彈性值相等,也可轉(zhuǎn)化為徑向正應(yīng)力與切應(yīng)力兩個(gè)分量連續(xù)再加應(yīng)力彈性值滿足圍巖峰前強(qiáng)度準(zhǔn)則,這兩個(gè)位置的應(yīng)力邊界作為定解條件以獲得塑性區(qū)半徑的表達(dá)式.

2.2.1ε0階問題

在圖3(a)的ε0階問題中,圓形隧道洞壁處作用均勻支護(hù)力pi,由式(15a)知無窮遠(yuǎn)處只作用均勻徑向荷載q、無剪切荷載,屬于側(cè)壓力系數(shù)λ=1 即靜水壓力下經(jīng)典的隧道問題,相應(yīng)ε0階圍巖彈性區(qū)應(yīng)力為[28]

式(20)已滿足的定解條件,包括無窮遠(yuǎn)處應(yīng)力邊界,彈塑性交界線外側(cè)的圍巖峰前強(qiáng)度準(zhǔn)則、切應(yīng)力塑性值與彈性值相等,再根據(jù)彈塑性交界線外側(cè)徑向正應(yīng)力的塑性值與彈性值相等,即r=Rp=R0時(shí)式(19a)中的σr(op)等于式(20a)中的,得ε0階隧道塑性區(qū)半徑的攝動(dòng)解析解為[28]

2.2.2ε1階問題

在ε0階圍巖彈性區(qū)應(yīng)力和隧道塑性區(qū)半徑解析解的基礎(chǔ)上,ε1階問題的待求量有,R1(θ);式(15b)為ε1階隧道無窮遠(yuǎn)處的應(yīng)力邊界,屬于ε1階問題的定解條件之一.

在ε1階彈塑性交界線外側(cè)r=Rp=R0[1-εR1(θ)]時(shí)的定解條件,包括式(22a)—徑向正應(yīng)力的塑性值和彈性值相等、式(22b)—切應(yīng)力的塑性值和彈性值相等和式(22c)—應(yīng)力彈性值滿足圍巖峰前強(qiáng)度準(zhǔn)則

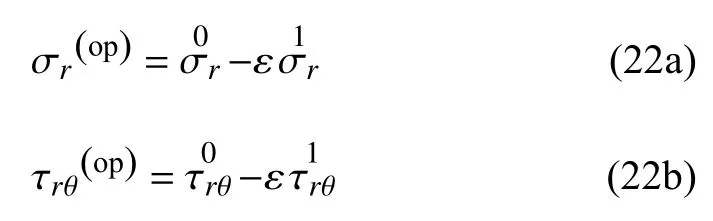
將式(22)在r=R0處按泰勒級(jí)數(shù)展開,根據(jù)展開式兩邊攝動(dòng)參數(shù)ε一次項(xiàng)的系數(shù)相等并代入式(19a)、式(19c)和式(20),整理得

將ε1階隧道無窮遠(yuǎn)和r=R0處的應(yīng)力邊界即式(15b)、式(23a)分離常數(shù)項(xiàng)、三角函數(shù)項(xiàng)后變?yōu)?/p>

由式(24)可知,ε1階應(yīng)力邊界包括常數(shù)項(xiàng)和cos(2θ)或sin(2θ)項(xiàng)兩部分,可設(shè)應(yīng)力函數(shù)=g1(r)+g2(r)cos(2θ),代入相容方程式(10)并根據(jù)常數(shù)項(xiàng)和cos(2θ)項(xiàng)的系數(shù)分別等于0 得

另設(shè)r=et,則式(25)變?yōu)?/p>

可見,式(26)為兩個(gè)獨(dú)立的4 階常系數(shù)齊次微分方程,式(26a)的特征根k1=k2=0,k3=k4=2,式(26b)的特征根k5=4,k6=2,k7=0,k8=-2,故式(26)的通解為

式中,A1,B1,C1,D1;A2,B2,C2,D2均為待定系數(shù).

將式(28b)代入式(23b)得

將式(21)和式(29)代入Rp=R0[1-εR1(θ)],得ε1階隧道塑性區(qū)半徑的攝動(dòng)解析解為

2.2.3εn階問題

在ε1階圍巖彈性區(qū)應(yīng)力和隧道塑性區(qū)半徑解析解的基礎(chǔ)上,ε2階問題的待求量有,R2(θ).按2.2.2 節(jié)的分析思路求得

將式(21)、式(29)和式(32)代入Rp=R0·[1-εR1(θ)-ε2R2(θ)],得ε2階隧道塑性區(qū)半徑的攝動(dòng)解析解為

在ε2階圍巖彈性區(qū)應(yīng)力和隧道塑性區(qū)半徑解析解的基礎(chǔ)上,ε3階問題的待求量有,R3(θ).按2.2.2 節(jié)的分析思路求得

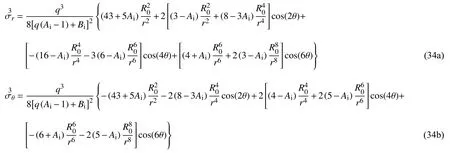
將式(21)、式(29)、式(32)和式(35)代入Rp=R0[1-εR1(θ)-ε2R2(θ)-ε3R3(θ)],得ε3階隧道塑性區(qū)半徑的攝動(dòng)解析解為

依次類推,可得到εn階隧道塑性區(qū)半徑的攝動(dòng)解析解.本文基于統(tǒng)一強(qiáng)度理論所建立的非靜水壓圓形隧道塑性區(qū)半徑的脆塑性攝動(dòng)解析解,考慮了中間主應(yīng)力效應(yīng)和脆性軟化的共同影響,包括Mohr-Coulomb 強(qiáng)度準(zhǔn)則解答(b=0)[17-18]和反映中間主應(yīng)力效應(yīng)不同程度的系列強(qiáng)度準(zhǔn)則解答(0＜b≤1),且理想彈塑性模型解答為其特例[17-18],具有重要理論意義和良好工程應(yīng)用前景.

2.3 攝動(dòng)階數(shù)

隨著攝動(dòng)階數(shù)n的提高,非靜水壓力下隧道塑性區(qū)半徑的解析表達(dá)式越復(fù)雜,有必要在保證精度的前提下盡可能降低攝動(dòng)階數(shù).取文獻(xiàn)[29]中的隧道算例,彈-脆-塑性圍巖強(qiáng)度參數(shù)ci=1.8 MPa,φi=45°,cr=0.7 MPa,φr=32°,理想彈塑性圍巖強(qiáng)度參數(shù)cr=ci=1.8 MPa,φr=φi=45°.圖4 為ε0階、ε1階和ε2階隧道塑性區(qū)邊界線的對(duì)比,其中a=3 m,pi=0.5 MPa,q=30 MPa,ε=0.3 對(duì)應(yīng)λ=0.7,b=0,0.5,1.

由圖4 可以看出,對(duì)于所取的隧道算例,無論是不同的材料模型還是不同的統(tǒng)一強(qiáng)度理論參數(shù)b,ε2階隧道塑性區(qū)邊界線與ε0階的圓形相差明顯,但相比ε1階的變化很小,且ε3階與ε2階的塑性區(qū)邊界線基本重合(圖4 中未給出ε3階),故ε2階攝動(dòng)解既滿足精度又表達(dá)較簡潔,下文設(shè)定統(tǒng)一取到ε2階.

圖4 ε0 階、ε1 階和ε2 階塑性區(qū)邊界線的對(duì)比Fig.4 Comparison of plastic boundary for the ε0,ε1 and ε2 problems

此外,兩種材料模型下隧道塑性區(qū)均為雙軸對(duì)稱的類橢圓,可只比較第I 象限的塑性區(qū)形狀和大小;彈-脆-塑性模型下隧道塑性區(qū)范圍相比理想彈塑性模型下的要大得多,b=0,0.5,1 時(shí)理想彈塑性模型ε2階類橢圓塑性區(qū)的長/短軸分別相差0.52,0.41,0.36 m,相應(yīng)彈-脆-塑性模型的分別相差0.82,0.58,0.48 m;統(tǒng)一強(qiáng)度理論參數(shù)b對(duì)隧道塑性區(qū)范圍的影響顯著而對(duì)塑性區(qū)形狀的影響較小,且b=0 時(shí)的隧道塑性區(qū)范圍最大,于是在4.1 節(jié)和4.3 節(jié)中僅討論b=0.

圖5 為彈-脆-塑性模型下ε2階隧道彈塑性交界線內(nèi)側(cè)塑性應(yīng)力與外側(cè)彈性應(yīng)力在第I 象限的分布情況,未標(biāo)出為零的切應(yīng)力.可以看出,徑向正應(yīng)力在彈塑性交界線處連續(xù),而切向正應(yīng)力的外側(cè)彈性值高于內(nèi)側(cè)塑性值,滿足定解條件和脆塑性強(qiáng)度的要求;同理,可圖示驗(yàn)證在彈塑性交界線外側(cè)三個(gè)應(yīng)力分量的彈性值與塑性值相等.

圖5 彈塑性交界線處的應(yīng)力分布Fig.5 Stress distribution at the elastic-plastic boundary

2.4 適用范圍

對(duì)于非靜水壓力下圓形隧道的彈塑性分析,根據(jù)洞周圍巖是否屈服分為三種情況:純彈性狀態(tài)、洞周部分圍巖屈服、洞周圍巖全部屈服,對(duì)應(yīng)隧道無塑性區(qū)、塑性區(qū)局部包圍隧道和塑性區(qū)完全包圍隧道.以側(cè)壓力系數(shù)λ小于1 即0＜ε＜1 為例,先假定塑性區(qū)完全包圍隧道,此時(shí)類橢圓塑性區(qū)的長軸位于θ=0°處、短軸位于θ=90°處,將θ=0°和90°代入式(33)并記為Rp(θ=0°)和Rp(θ=90°),再探討三種屈服情況的判別.

若Rp(θ=90°)≥a,則塑性區(qū)完全包圍隧道,本文攝動(dòng)解析解適用于求解此情況下隧道的塑性區(qū)半徑和彈性區(qū)應(yīng)力分布.

若Rp(θ=0°)≥a但Rp(θ=90°)＜a,則塑性區(qū)局部包圍隧道,本文攝動(dòng)解析解不適用這種情況.根據(jù)塑性區(qū)邊界線與隧道洞壁相交可求出塑性區(qū)的范圍,令Rp=a代入式(33)以確定塑性區(qū)邊界線與隧道洞壁的交點(diǎn).

取文獻(xiàn)[30]中的理想彈塑性軟巖隧道算例:a=1 m,pi=0 MPa,q=1 MPa,ε=0.2 對(duì)應(yīng)λ=0.8,cr=ci=0.276 MPa,φr=φi=35°,b=0,0.5,1.圖6為按2.2 節(jié)求得的隧道塑性區(qū)邊界線,其中b=0,0.5 時(shí)塑性區(qū)完全包圍隧道,b=1 時(shí)塑性區(qū)局部包圍隧道、塑性區(qū)邊界線與隧道洞壁相交于A點(diǎn),僅能從A點(diǎn)估算塑性區(qū)范圍.

圖6 塑性區(qū)邊界線的確定Fig.6 Determination of plastic boundary

若Rp(θ=0°)＜a,則隧道處于純彈性狀態(tài),由基爾希公式求圍巖應(yīng)力分布.

此外,攝動(dòng)參數(shù)ε可依據(jù)隧道所處地應(yīng)力場即ε=1-λ確定,并按照上述思路判定本文攝動(dòng)解析解的適用性;同時(shí),攝動(dòng)參數(shù)ε越小越好,建議側(cè)壓力系數(shù)λ＜1 時(shí)攝動(dòng)參數(shù)ε＜0.5.

3 對(duì)比驗(yàn)證

為驗(yàn)證本文非靜水壓力下圓形隧道塑性區(qū)半徑攝動(dòng)解析解的正確性和合理性,分別與文獻(xiàn)復(fù)變函數(shù)法、攝動(dòng)法、數(shù)值模擬和總荷載不變法的結(jié)果進(jìn)行比較,并探討攝動(dòng)參數(shù)ε的取值范圍.需要說明的是,這4 種方法均基于Mohr-Coulomb 強(qiáng)度準(zhǔn)則,對(duì)應(yīng)本文的統(tǒng)一強(qiáng)度理論參數(shù)b=0,除總荷載不變法采用彈-脆-塑性模型以外都假定圍巖符合理想彈塑性模型即cr=ci,φr=φi.

3.1 復(fù)變函數(shù)法

呂愛鐘等[10]建立了非靜水壓力下圓形隧道塑性區(qū)半徑的復(fù)變函數(shù)解答.取文獻(xiàn)[10]中的隧道算例:a=2 m,pi=0 MPa,q=15 MPa,cr=ci=1 MPa,φr=φi=30°,ε=0.1,0.2,0.3 分別對(duì)應(yīng)λ=0.9,0.8,0.7.圖7 中本文與文獻(xiàn)[10]的隧道塑性區(qū)邊界線吻合良好,驗(yàn)證了本文解析解的合理性,且隨著側(cè)壓力系數(shù)λ趨近于1,兩種方法的結(jié)果差異在減小;Kastner 法忽略圍巖彈塑性發(fā)展過程,較本文攝動(dòng)法低估塑性區(qū)范圍0.77～1.89 m.

圖7 對(duì)比復(fù)變函數(shù)法的塑性區(qū)邊界線Fig.7 Comparisons with the plastic boundary of the complex variable function method

3.2 攝動(dòng)法

魏悅廣[17]從側(cè)壓力系數(shù)λ＞1 出發(fā),推導(dǎo)了非靜水壓力下圓形隧道塑性區(qū)半徑的攝動(dòng)解答.取文獻(xiàn)[17]中的兩組隧道算例:(1)a=1 m,pi=0 MPa,q=13.1 MPa,cr=ci=2.45 MPa,φr=φi=30°,ε=-0.125 對(duì)應(yīng)λ=1.125;(2)a=1 m,pi=0 MPa,q=24.5 MPa,cr=ci=2.45 MPa,φr=φi=30°,ε=-0.2 對(duì)應(yīng)λ=1.2.本文隧道塑性區(qū)邊界線與文獻(xiàn)[17]的完全吻合,如圖8 所示,證明了本文解析解的正確性,同時(shí)得出:本文解析解適用于側(cè)壓力系數(shù)大于1 的情況,表明攝動(dòng)參數(shù)ε＜0 是可行的.

圖8 兩種攝動(dòng)解答的對(duì)比Fig.8 Comparisons of two perturbation solutions

3.3 數(shù)值模擬

Bagheri 等[16]采用二維彈塑性有限元程序,開展了非靜水壓力下圓形隧道塑性區(qū)半徑的數(shù)值模擬,擬合出參數(shù)d以描述4 種埋深下隧道塑性區(qū)半徑的變化,其中d=Rp(ε≠0)/Rp(ε=0)代表非靜水壓力下與靜水壓力下圓形隧道塑性區(qū)半徑的比值.取文獻(xiàn)[16]中的隧道算例:pi=0 MPa,cr=ci=0.55 MPa,φr=φi=24°.本文攝動(dòng)法參數(shù)d與文獻(xiàn)[16]的數(shù)值模擬基本吻合,如圖9 所示,同樣證明了本文解析解的合理性,同時(shí)得出:本文解析解在側(cè)壓力系數(shù)λ小于1 和大于1 時(shí)均適用.

圖9 不同ε 下參數(shù)d 的比較Fig.9 Comparisons of the parameter d with different ε

3.4 總荷載不變法

董海龍和高全臣[14]獲得了非靜水壓力下圓形隧道塑性區(qū)半徑的總荷載不變法解答.取2.3 節(jié)中的彈-脆-塑性隧道算例,ε=0.1,0.2,0.3 分別對(duì)應(yīng)λ=0.9,0.8,0.7.圖10 中兩種方法的隧道塑性區(qū)邊界線吻合較好,表明了本文解析解在彈-脆-塑性模型下的有效性.

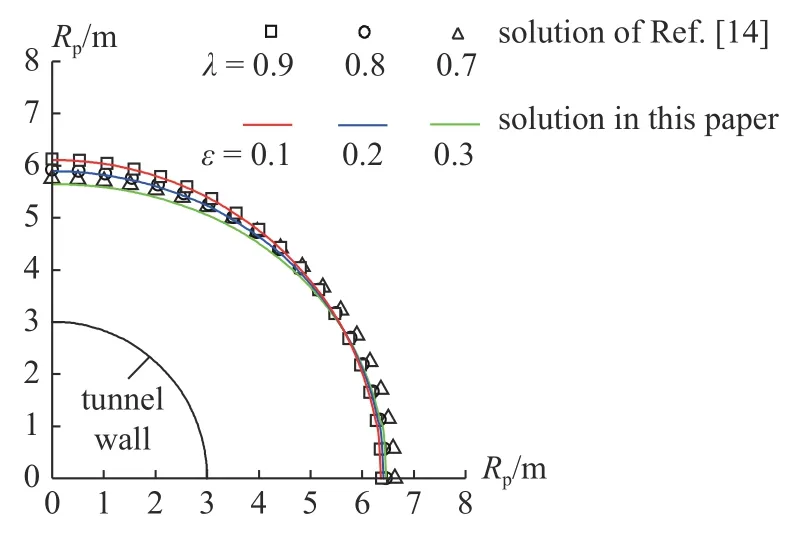
圖10 對(duì)比總荷載不變法的塑性區(qū)邊界線Fig.10 Comparisons with the plastic boundary of the constant assumption of total loads

4 參數(shù)分析

4.1 攝動(dòng)參數(shù)

隧道算例與2.3 節(jié)相同,圖11 為不同攝動(dòng)參數(shù)ε下兩種材料模型的隧道塑性區(qū)邊界線變化.可以看出,隨著ε增加隧道塑性區(qū)邊界線沿豎直向下移動(dòng)、沿水平向右移動(dòng),且豎直方向上的變化更為明顯.另外,對(duì)比圖11(a)和圖11(b)知,彈-脆-塑性模型的塑性區(qū)范圍較理想彈塑性模型的明顯增大、受攝動(dòng)參數(shù)ε的影響與變化也更顯著,表明理想彈塑性模型所得隧道塑性區(qū)范圍較小(相差2.05～2.46 m),工程中宜采用彈-脆-塑性模型.

圖11 不同ε 下塑性區(qū)邊界線Fig.11 Plastic boundary with different ε

4.2 中間主應(yīng)力

隧道算例與2.3 節(jié)相同,圖12 為不同統(tǒng)一強(qiáng)度理論參數(shù)b下兩種材料模型的隧道塑性區(qū)邊界線變化.可以看出,隨著參數(shù)b即中間主應(yīng)力影響程度的增加,隧道塑性區(qū)范圍在不斷減小,體現(xiàn)了中間主應(yīng)力對(duì)圍巖強(qiáng)度的提高作用,尤其是彈-脆-塑性模型;Mohr-Coulomb 強(qiáng)度準(zhǔn)則(圖2(b)中b=0),相比b等于0.5 或1 沒有利用圍巖的強(qiáng)度潛能,理想彈塑性模型下b=0 時(shí)塑性區(qū)長軸較b=0.5,1 時(shí)增大了0.30,0.43 m,彈-脆-塑性模型下b=0 時(shí)塑性區(qū)長軸較b=0.5,1 時(shí)增大了1.07,1.52 m.

圖12 不同b 下塑性區(qū)邊界線Fig.12 Plastic boundary with different b

4.3 脆性軟化

取文獻(xiàn)[30]中的隧道算例:a=1 m,pi=0 MPa,q=1 MPa,b=0,ε=0.3 對(duì)應(yīng)λ=0.7;軟巖的彈-脆-塑性強(qiáng)度參數(shù)ci=0.276 MPa,φi=35°,cr=0.055 MPa,φr=30°,理想彈塑性強(qiáng)度參數(shù)cr=ci=0.276 MPa,φr=φi=35°;硬巖的彈-脆-塑性強(qiáng)度參數(shù)ci=0.173 MPa,φi=55°,cr=0.061 MPa,φr=52°,理想彈塑性強(qiáng)度參數(shù)cr=ci=0.173 MPa,φr=φi=55°.圖13 為不同圍巖類別下隧道的塑性區(qū)邊界線變化,表明兩種材料模型下軟巖隧道的塑性區(qū)范圍差異較硬巖隧道的顯著(僅限于所取文獻(xiàn)算例).

圖13 不同圍巖類別下塑性區(qū)邊界線Fig.13 Plastic boundary for different rock masses

圖14 為脆性軟化即圍巖峰后強(qiáng)度參數(shù)對(duì)軟巖隧道塑性區(qū)邊界線的影響,硬巖隧道亦然.可以看出,脆性軟化幅度越大即圍巖的峰后強(qiáng)度參數(shù)越小,塑性區(qū)邊界線越大:峰后黏聚力cr平均每減小0.01 MPa,塑性區(qū)長軸增加0.09 m、短軸增加0.07 m;峰后內(nèi)摩擦角φr平均每減小1°,塑性區(qū)長軸增加0.06 m、短軸增加0.05 m.

圖14 峰后強(qiáng)度參數(shù)對(duì)軟巖隧道塑性區(qū)邊界線的影響Fig.14 Effect of post-peak strength parameter on the plastic boundary of soft rock tunnel

5 結(jié)論

(1)基于統(tǒng)一強(qiáng)度理論所建立的非靜水壓圓形隧道塑性區(qū)半徑的脆塑性攝動(dòng)解析解,合理考慮了圍巖強(qiáng)度的中間主應(yīng)力效應(yīng)和脆性軟化,可得到Mohr-Coulomb 強(qiáng)度準(zhǔn)則解答和反映中間主應(yīng)力效應(yīng)不同程度的系列強(qiáng)度準(zhǔn)則解答,能獲得真實(shí)地應(yīng)力場下較為準(zhǔn)確的非圓塑性區(qū)邊界線,將有效指導(dǎo)以收斂約束法為基礎(chǔ)的隧道支護(hù)選型和剛度設(shè)計(jì),具有重要理論意義和良好工程應(yīng)用前景.

(2)對(duì)比文獻(xiàn)復(fù)變函數(shù)法、攝動(dòng)法、數(shù)值模擬和總荷載不變法,驗(yàn)證了本文隧道塑性區(qū)半徑攝動(dòng)解析解的正確性和合理性,亦表明攝動(dòng)參數(shù)可正可負(fù),并根據(jù)圍巖屈服情況給出所得解析解的適用范圍.攝動(dòng)參數(shù)對(duì)隧道類橢圓形塑性區(qū)的大小和長/短軸變化都有明顯影響,且豎直方向上的塑性區(qū)變化更為突出.

(3)隨著中間主應(yīng)力效應(yīng)的增加,隧道的塑性區(qū)范圍顯著減小,Mohr-Coulomb 強(qiáng)度準(zhǔn)則解答的塑性區(qū)范圍最大而偏保守,尤其是彈-脆-塑性圍巖.圍巖峰后強(qiáng)度越低則隧道的塑性區(qū)范圍越大,理想彈塑性模型忽略圍巖峰后強(qiáng)度跌落相比彈-脆-塑性模型得到的塑性區(qū)偏小.