鎢合金長桿彈撞擊厚壁柱形目標臨界跳飛角計算模型
金文, 門建兵, 蔣建偉, 彭嘉誠, 李梅
(北京理工大學 爆炸技術國家重點實驗室, 北京 100081)
0 引言
目前,隨著電磁炮等新型發射平臺的發展,小口徑桿式穿甲彈可用于防空反導領域執行防空攔截任務。由于傳統火炮發射的桿式彈初速一般1 400~1 800 m/s,打擊目標多為具有平板結構厚靶或多層靶裝甲目標,而防空反導領域打擊的目標多為具有柱面殼體結構目標,如GBU-31(V)3B/4B空地導彈戰斗部采用厚度25 mm的特種合金鋼殼體,這都對長桿彈毀傷能力提出了更高要求,而長桿彈與厚壁柱形目標在高速撞擊時是否發生跳飛,是長桿彈能否有效毀傷來襲目標的關鍵問題。

以上國內外學者主要集中于研究鎢合金長桿彈撞擊平面裝甲目標時的跳飛規律,對于高速長桿彈撞擊厚壁柱形目標的跳飛規律研究報道較少。而長桿彈作用于厚壁柱形目標易受著靶條件影響,發生跳飛時便無法對厚壁柱形目標形成穩定侵徹,進而無法侵入厚壁柱形目標造成更大毀傷效應。為確定長桿彈撞擊厚壁柱形目標時跳飛的邊界,需要建立長桿彈撞擊厚壁柱形目標時臨界跳飛角計算模型。
本文采用LS-DYNA3D顯式動力學仿真軟件,對不同著靶條件下鎢合金長桿彈撞擊厚壁柱形目標進行數值模擬,在此數值模擬結果基礎上,引入著速、命中偏移角,建立基于Rosenberg模型的臨界跳飛角修正計算模型。在已知長桿彈著速與命中偏移角條件下,能夠預測其是否發生跳飛,對于評估長桿彈對厚壁柱形目標毀傷效果具有一定的指導意義。
1 幾何模型與基本假設
長桿彈在具有一定命中偏移角,即以非理想狀態撞擊目標時,圓柱形殼體弧形結構無法保證穩定的著靶條件,長桿彈與目標靶板接觸時的作用面不足以支撐長桿彈形成侵徹,從而跳飛。
截取厚壁柱形目標圓柱部區段用于小口徑長桿彈撞擊厚壁柱形目標計算分析。如圖1(c)所示,過彈著點做目標圓柱體橫截面,為兩同心圓圍成的平面。圖1(a)中,彈芯軸線與橫截面所夾銳角為著角;圖1(b)中,臨界跳飛角為長桿彈撞擊靶板剛好發生跳飛時著角的大小(>,長桿彈跳飛;<,長桿彈侵徹);圖1(c)為命中偏移角=0°時長桿彈與厚壁柱形目標作用位置示意圖;在圖1(d)中,為殼體厚度、為目標外徑。定義彈芯軸線在橫截面上投影與彈著點法線所夾銳角為命中偏移角,過圓心作平行于彈芯投影的直線,彈著點到距離為偏移距離。
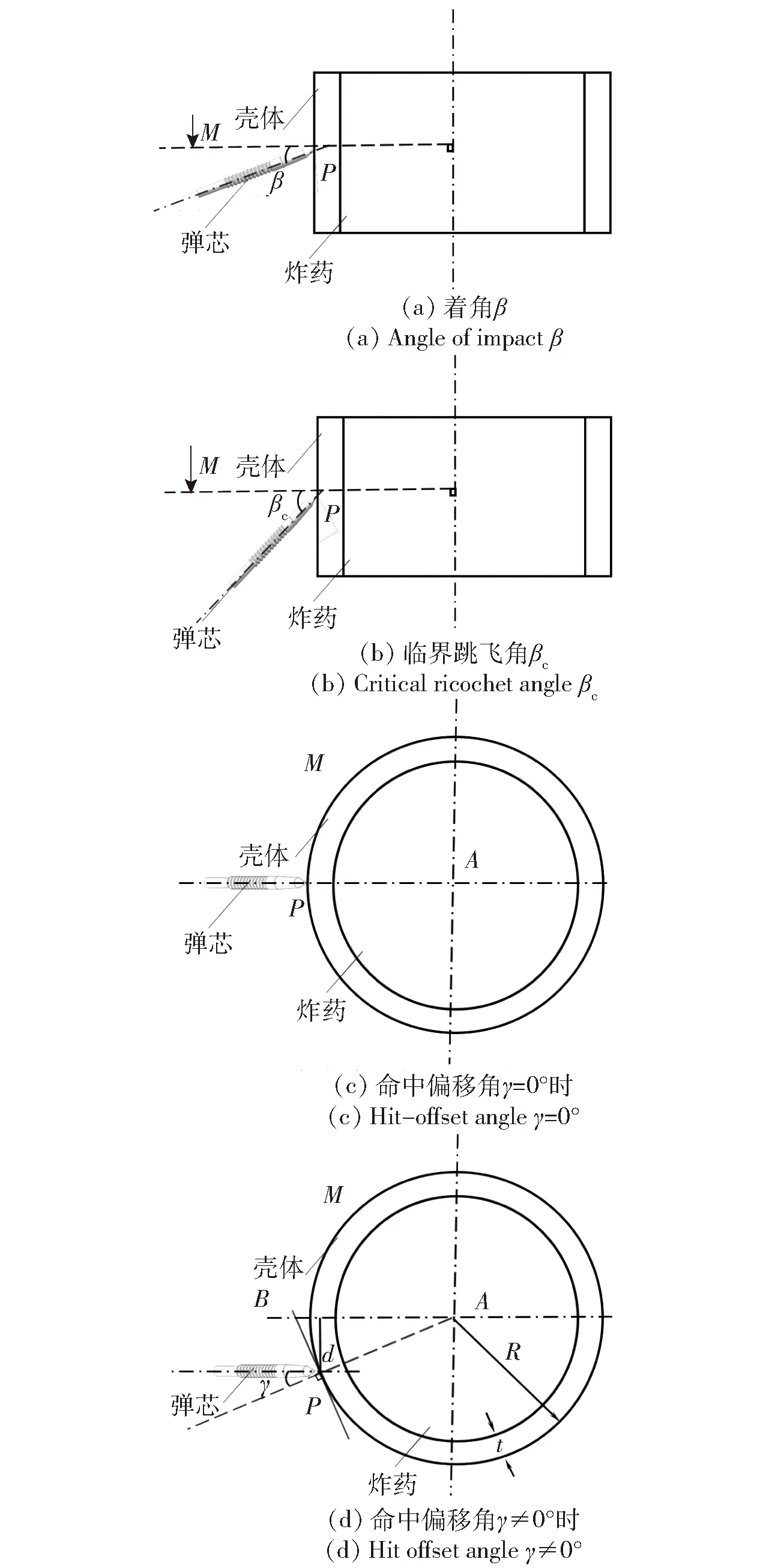
圖1 幾何模型參數示意圖Fig.1 Schematic diagram of parameters for the geometric model
圖2為Lee模型與Rosenberg模型對比結果。Lee等基于Rosenberg研究了靶板厚度對臨界跳飛角影響。對于薄靶而言,臨界跳飛角值增大4左右,因此本文中假設殼體厚度對臨界跳飛角影響可以忽略;對于厚壁柱形目標半徑,與命中偏移角關系為sin=(=1),則sin的物理含義為:對于具有任意半徑的厚壁柱形目標,長桿彈撞擊位置的相對偏移程度。

圖2 Lee模型[11]與Rosenberg模型[9]對比Fig.2 Lee model[11] versus Rosenberg model[9]
結合Rosenberg等研究結果,當長桿彈以著速作用于厚壁柱形目標時,臨界跳飛角可表示為關于著速、長桿彈材料密度、靶板侵徹阻力、彈體頭部速度、命中偏移角、殼體厚度、目標半徑的函數:
=(,,,,,,)
(1)
式中:、均為與彈靶材料相關常數;彈體頭部速度=0 m/s;目標半徑可由命中偏移角表征。
在上述基礎上提出以下基本假設:
1)Rosenberg模型適用于小型長桿彈撞擊厚壁柱形目標時臨界跳飛角計算,不考慮長徑比等因素對計算模型的影響;
2)忽略殼體厚度對臨界跳飛角影響,彈體頭部速度=0 m/s,命中偏移角可表征厚壁柱形目標半徑對臨界跳飛角影響;
3)長桿彈與厚壁柱形目標材料均勻性好,且在二者相互作用下其材料強度不發生變化;
4)厚壁柱形目標內部裝藥為惰性材料,暫不考慮炸藥裝藥起爆及炸藥類型對臨界跳飛角影響。
基于上述假設條件建立修正項,將著速、命中偏移角作為對臨界跳飛角影響的主要表征量。引入Alekseevskii模型中的彈尾臨界速度:

(2)
式中:為長桿彈屈服強度。假設、二者間相互獨立,且、對臨界跳飛角的影響效應可線性疊加;定義=為長桿彈撞擊厚壁柱形目標時相對于修正前的臨界跳飛角的修正因子。
綜上,選取尾臨界速度為基本量,根據量綱分析π定理對自變量進行無量綱化處理,(1)式可表示為

(3)
式中:為著速與彈尾臨界速度的比值;

(4)


(5)

(6)
、分別為特定命中偏移角和著速。
以上為基于Rosenberg計算模型應用于厚壁柱形目標幾何模型的修正模型建立方法。
2 修正計算模型
Tate等建立的臨界跳飛角預測計算模型為

(7)
式中:為長桿彈彈長;為長桿彈直徑。
Rosenberg等在Tate研究基礎上提出將非對稱力僅作用于彈體由于撞擊所侵蝕的質量上,避免了計算模型中出現桿長度項:

(8)
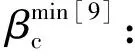

(9)


2.1 修正數據獲取
采用LS-DYNA3D顯式動力學軟件進行數值模擬計算,選用Solid164六面體Lagrange單元算法,采用常見長桿式穿甲彈中經常應用嚙齒式結構;長桿彈與殼體之間采用侵蝕接觸能更好的模擬長桿式穿甲彈穿甲過程中彈體破碎和侵蝕過程;長桿彈、殼體與炸藥之間均采用侵蝕接觸,并添加材料侵蝕關鍵字對炸藥單元進行約束。如圖3所示,具有軸對稱性質的工況建立其1/2有限元模型以減少計算時間,非軸對稱工況采用全模型建模。

圖3 彈靶作用有限元模型Fig.3 Finite element model of the projectile impacting the target
*MAT_ELASTIC_PLASTIC_HYDRO材料模型用于模擬鎢合金長桿彈在穿甲過程中發生的彈體侵蝕和破碎現象,采用Gruneisen狀態方程,長桿彈材料參數參考文獻[18]所用參數;靶板材料為30CrMnSiNi2A,內部裝藥采用惰性材料模型*MAT_PLASTIC_KINEMATIC表征。鎢合金、裝藥材料參數如表1、表2所示。
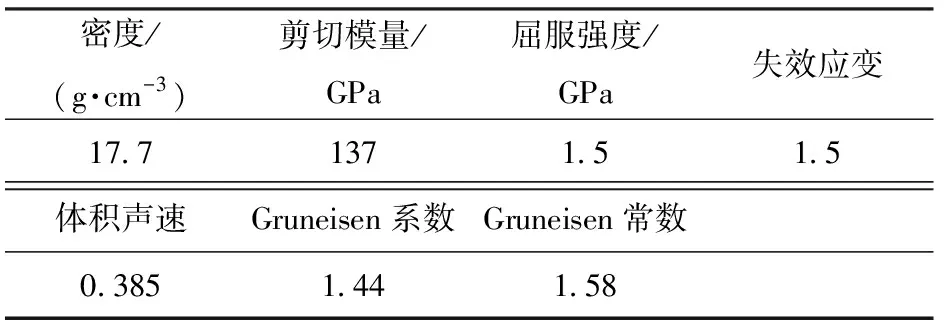
表1 鎢合金材料參數

表2 裝藥材料參數
對數值模擬計算模型的正確性進行驗證。Rosenberg等建立的臨界跳飛角計算模型中,臨界跳飛角只與彈靶材料特性有關,與其他因素無關。如圖4、圖5所示,設立對照數值模擬工況,著速=1 000 m/s,靶板沿法線方向速度270 m/s,著角53°時數值模擬結果跳飛狀態與Rosenberg等的試驗結果比對,其結果基本一致。在此基礎上,進一步研究長桿彈侵徹厚壁柱形目標時臨界跳飛規律。

圖4 典型條件下數值模擬結果Fig.4 Numerical simulation result under typical conditions

圖5 典型條件下試驗結果[10]Fig.5 Experimental result under typical conditions[10]
首先根據(9)式對臨界跳飛角進行初步預估,然后通過升降法逐漸逼近,最后確定臨界跳飛角區間,當區間足夠小時,可取區間極限平均值作為數值模擬計算估計值。考慮到計算能力的有限性,以相鄰兩不同著速、+1進行數值模擬,得到的臨界跳飛角可能處于同一區間,此時利用著速+2對速度區間[+2]近似線性估計,以確定著速時臨界跳飛角估計值。表3為著速為1 800 m/s時在臨界跳飛角區間為[70° 75°]時的侵徹過程圖。由表3對比可知,該速度下以70°著角侵徹厚壁柱形目標時,對比75°著角能夠形成明顯的侵徹過程——當著角為75°時,靶板法線與長桿彈軸線夾角逐漸增大,最后甚至趨于90°。
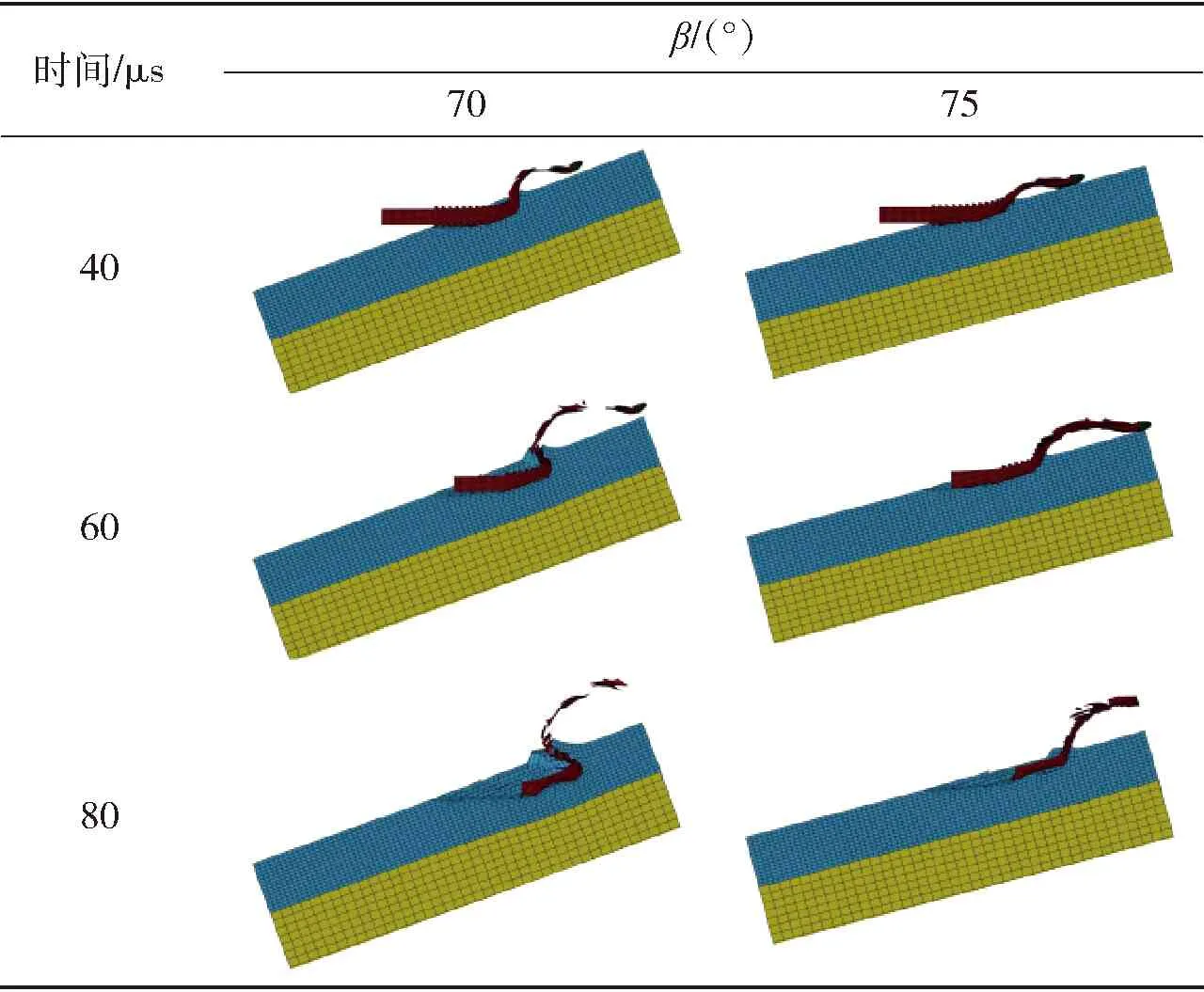
表3 著角為70°、75°各時刻侵徹狀態
2.2 修正函數建立
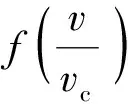
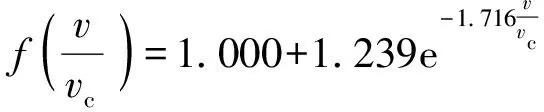
(10)

圖隨著速變化曲線 curve with impact velocity
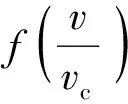
圖7為不同命中偏移角下(sin)值,以及(sin)隨sin變化的擬合曲線。
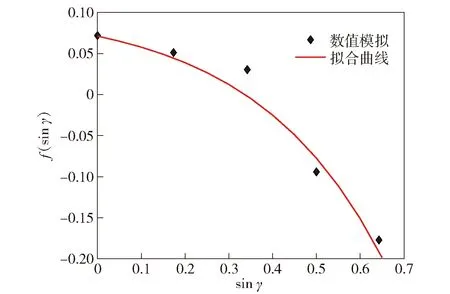
圖7 f(sin γ)隨命中偏移角γ變化曲線Fig.7 f(sin γ) curve with hit-offset angle
當=0°時,不考慮命中偏移角對臨界跳飛角的影響,此時
(sin)=0
(11)
圖7中隨著命中偏移角的增大,長桿彈形成穩定侵徹厚壁柱形目標的能力急速弱化,圖中擬合曲線表達式為
(sin)=0104 3-0033 10e3406sin
(12)
綜上,參考Lee等的研究方法,關于命中偏移角的修正因子函數形式為=+e形式。對命中偏移角進行無量綱化后,得到擬合曲線方程中各參數如表4所示。

表4 擬合曲線方程參數
將(10)式、(12)式代入(3)式、(4)式,可得到長桿彈撞擊厚壁柱形目標時臨界跳飛角的修正計算模型。
當=0°時:

(13)
當0°<≤40°時:

(14)
式中:命中偏移角可由交匯條件與目標結構決定,即用柱形目標半徑、命中偏移距離表示:
=arcsin ()
(15)
圖8為臨界跳飛角隨撞擊速度以及命中偏移角分布圖,可見長桿彈臨界跳飛角隨撞擊速度與命中偏移角的減小呈輻射狀減小。若定義長桿彈在典型彈目交匯條件(即=60°)作為過渡區,則可將圖8分為3大區域:
1)侵徹區:此區域內臨界跳飛角在65°以上。這一區域內影響臨界跳飛角變化的主導因素為著速,隨著速增大,臨界跳飛角受命中偏移角影響逐漸減弱,長桿彈著角支持其形成穩定侵徹;
2)過渡區:此區域內臨界跳飛角在60°左右,作為侵徹區與跳飛區的過渡區域;
3)跳飛區:這一區域內影響臨界跳飛角變化的主導因素為柱形目標弧形殼體結構,即隨著命中偏移角的增大,臨界跳飛角受著速影響逐漸減弱,長桿彈著角并不能支持其形成侵徹,發生跳飛現象。

圖8 臨界跳飛角分布Fig.8 Distribution of the critical ricochet angel
3 模型校核
圖9為命中偏移角=30°時各著速下長桿彈的著靶狀態與Rosenberg計算模型和修正計算模型對比圖。此時臨界跳飛角變化趨勢與Rosenberg等計算模型基本一致;臨界跳飛角隨著速增大而逐漸增大,最終趨于平緩;命中偏移角的存在大大減小了臨界跳飛角,并且隨速度增加,命中偏移角的影響程度逐漸降低。仿真結果中跳飛與侵徹數據點較為一致地分布于修正計算模型兩側。

圖9 γ=30°時修正前后計算模型與數值模擬結果校核Fig.9 Verified computational model and numerical simulation results before and after correction when γ=30°
選取不同著速、命中偏移角、著角進行數值模擬。圖10為任取命中偏移角、著速時,數值模擬數據點分布于該臨界跳飛角修正計算模型所形成的分界面上下兩側,較好地區分了侵徹- 跳飛。因此,該計算模型能夠準確反映長桿彈撞擊厚壁柱形目標時跳飛的邊界,具有一定準確性與適用性。
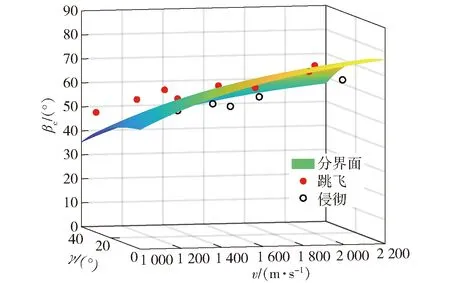
圖10 侵徹- 跳飛分布Fig.10 Penetration-ricochet distribution
4 結論
本文針對不同著靶條件下鎢合金長桿彈撞擊厚壁柱形目標的跳飛問題,基于經試驗驗證的數值模擬手段,量化分析著速、命中偏移角與臨界跳飛角關系,建立確定鎢合金長桿彈撞擊厚壁柱形目標跳飛邊界的工程計算模型,可作為實際工程參考。得出以下主要結論:
1)采用數值模擬方法,通過對長桿彈以不同著靶條件撞擊厚壁柱形目標進行仿真計算,獲得著速取值為1 000~2 200 m/s的鎢合金長桿彈撞擊厚壁柱形目標時的臨界跳飛角,數值模擬結果與Rosenberg等的仿真、試驗結果基本一致。
2)引入包含著速、命中偏移角的修正因子,對Rosenberg臨界跳飛角計算模型進行修正,并構造鎢合金長桿彈撞擊厚壁柱形目標時臨界跳飛角計算模型。
3)基于不同著靶條件下的數值模擬結果,對鎢合金長桿彈撞擊厚壁柱形目標時臨界跳飛角計算模型進行校核驗證,校驗結果表明,此計算模型具有一定普適性與準確性。

