鐵道車輛探傷設備動態多階段可靠性評估

趙榮華，彭一真，陳佳豪，王 宇

（1.中國鐵路西安局集團有限公司，陜西西安 710054；2.重慶大學機械與運載工程學院，重慶 400044；3.西安交通大學機械工程學院，陜西西安 710049）

0 引言

隨著我國鐵路運營里程、技術標準和裝備水平的大幅躍升，保障鐵道車輛長期安全可靠穩定運行、避免重大事故發生，已經成為了工程領域的重大課題。在這一迫切需求的驅動下，各類先進鐵道車輛探傷設備得到了廣泛應用。由于其能及時發現隱患、管控風險，探傷設備在列車管理、運營和檢修中的作用不斷突顯。而一旦探傷設備發生故障導致鐵道車輛隱患無法及時發現，將造成難以估量的損失。對鐵道車輛探傷設備的可靠性水平進行動態地評估，并據此制定合理維修保障策略以避免重大損失的發生，可謂勢在必行。為此，本文在經典AMSAA 模型的基礎上，考慮鐵道車輛探傷設備實際維修策略，提出了一種具有變點的非時齊Poisson 動態可靠性評估模型以評估設備的動態可靠性，并預測設備未來的故障頻率和故障發生時間。對西安東車輛段的某磁粉探傷設備故障數據的分析結果表明，所提出方法能準確地預測未來故障的發生頻次。

1 AMSAA 動態可靠性評估模型

鐵道車輛探傷設備是一類復雜的可維修機電一體化系統，在其全壽命周期中不可避免地會經歷“運行—故障—分析維修—再運行”的過程。而隨著維修活動或者技術改造活動的開展，探傷設備本體可靠性必然會不斷變動。鐵道車輛探傷設備作為一種與人民生命財產安全休戚相關的關鍵裝備，有必要根據設備的故障數據對設備變動的可靠性水平進行及時地評定，以規避不必要風險、避免重大損失的發生，并據此判斷實施的維修活動是否對設備可靠性水平的保持起到積極的效果。

針對可維修系統故障數據的動態可靠性評估模型被錢學森教授歸為“變動統計學”的領域，具有評估對象復雜，試驗次數與試驗條件有限等特點[1]。相較于傳統設計可靠性而言，對服役中的復雜系統顯得尤為重要，在分析方法上也更為復雜。為解決可維修系統的動態可靠性評定問題，國內外開展了各種研究。20 世紀50 年代末，Duane 在對航空發動機、噴氣發動機等5 種復雜裝備近600 萬小時的故障維修數據的分析中發現了累積工作時間與累積故障率具有雙對數線性規律，工程上稱之為Duane模型，其具有應用簡單適用范圍廣等特點[2]。隨后，美軍裝備系統分析中心的Crow 在Duane 模型的啟發下，引入一個以冪律函數為均值函數的非時齊泊松過程模型，并用以描述故障累積次數隨時間的變化規律。在此基礎上，Crow 借助點過程理論給出了模型的統計推斷和假設檢驗方法，克服了Duane 模型估計精度低，檢驗方法粗糙的問題[3]，工程上將這一模型稱為AMSAA 模型。目前AMSAA 模型已經被廣泛地應用在可靠性增值、可靠性趨勢分析以及動態可靠性評估等多個領域[4]，并被包括國際電工委員會IEC—TC—56（CO）150 在內的多個國際標準及美軍標準所采納。

令一可維修復雜系統在時間區間（0，t）累積發生故障數被記為N（t），則在AMSAA 模型中，N（t）服從以下一個隨機過程，即：

其中，Pr［·］代表事件發生概率，N（t）代表（0，t）時刻內得故障計數，k 代表故障計數，而m（t）=E［N（t）］則代表故障的均值函數。在AMSAA 模型中，m（t）采用經典的冪律函數進行描述，因此在文獻中AMSAA 模型也常被稱為冪律模型，即：

其中，λ（t）為故障率函數，也稱為瞬時故障強度函數，其值越小則表示系統的可靠性水平越高；a，b 分別為模型的比例參數和冪律參數。在AMSAA 模型中參數決定了系統可靠性的發展變動趨勢。當b=0 時，可維修系統的可靠性水平保持恒定。當0＜b≤1 時，可維修系統可靠性水平隨時間具有增值的趨勢。當b＞1 時，可維修系統可靠性水平隨時間有劣化趨勢。

設系統的失效時間依次被記錄為0＜t1＜t2＜…tn，依照泊松過程的獨立增量性質，每次故障發生是一個獨立事件。因此基于概率的乘法律，n 次故障分別在t1，t2，…tn等n 個時間點發生的概率能被計算為：

其中，Pr［N（ti）-N（ti-1）=0］表示在開區間（ti，ti-1）上發生0 次故障，λ（ti）表示在ti時刻發生一次故障。將式（1）和式（3）代入式（4），則有：

2 變點動態多階段可靠性評估模型

盡管經典AMSAA 模型通過冪律參數b 的調整，能夠適應于具有凹性、凸性或者線性等不同可靠性變動特點的對象或場景，并已經在風力發電機、石化管道壓縮機等領域得到成功應用。但由于經典AMSAA 模型均值函數為連續冪律函數，因此它的主要局限在于其只適用于可靠性連續緩慢變動的場景。對于鐵道車輛探傷系統這類與人民生命財產安全休戚相關的設備而言，定期的大檢大修、技術改造必不可少。而在經歷大檢大修或大型技術改造后，探傷設備的可靠性水平通常會在時間軸上呈現突變的特點，因此不能直接適用于經典的AMSAA 模型。為了解決這一問題，本文提出了一種變點動態多階段可靠性評估模型，其融合一種自適應變閾值的序貫變點識別技術——CUSUM方法[4]，實現對具有多個可靠性變動階段的可靠性變動過程的分割、建模與動態預測。

實際工程中，探傷設備可靠性水平的突變主要是故障強度的突變，經常表現為平均兩次故障間隔時間（MTBF）在均值上的突變。有鑒于此，在CUSUM 方法的框架下，“可靠性變動過程”的突變點有無問題，可以轉化一個基于序貫概率比檢驗的假設檢驗問題。而將序貫概率比作為一個隨機變量的和，那么“可靠性變動過程”的突變點位置識別問題可以轉化為一個鞅的停時問題[5]。

首先，給出如下兩個假設：

其中，θ 代表檢驗的變動參數，在針對探傷設備可靠性變動過程即為MTBF；變動前的θ0可以通過運行初始時刻的故障數據獲得；變動后的θ1則可以通過3 西格瑪準則進行設定。基于此，借助序貫概率比檢驗方法（SPRT），檢驗統計量可以被表示為一個遞歸的形式，即：

其中，gk=0，yk代表了故障時間數據。進一步地，檢驗過程的停時（或階段分割時間）ta可被定義為：

其中，h 表示容許產生偏差的門限。基于式（11）、（12），可靠性變動過程可以被自適應地分割為多個階段，由此可以利用不同階段的數據，基于式（1）～（8），推斷不同階段的模型參數，記為，并評定系統在不同階段的可靠性變動。

3 案例分析

微機控制輪對專用熒光磁粉探傷機適用于普通貨車、客車輪軸不分解狀態下對車輪、制動盤和車軸外露部位的濕法熒光磁粉探傷作業。它能高效、準確、清晰地無損檢測到輪軸外露表面或近表面的裂紋（缺陷），是鐵路貨車、客車輪軸不分解狀態下對外露表面或近表面磁粉探傷的常用設備。在案例分析中，采用所提出的變點動態多階段可靠性評估模型，分析了西安鐵道車輛段某型微機控制輪對熒光磁粉探傷機2017—2020 年共4 年內的故障時間數據以驗證所提出方法的有效性。

圖1a）展示了4 年內共67 次故障累積數對時間的變化規律，其中將2017 年1 月1 日記為時間軸的原點位置。從圖1a）可以發現，從2017 年1 月1 日起經歷約580 d，共發生約50 次故障，在這期間故障強度在總體穩定中略有增高。在580 d 到600 d 附近，故障強度顯著下降，平均故障間隔時間增加，探傷機可靠性得到明顯提升。而從2017年1 月1 日起經歷約600 d 之后，共發生17 次故障，同樣地在這一階段故障強度穩定中略有增高，這表明可靠性水平進入了另一個新的緩慢下降區間。由于傳統的AMSAA 模型明顯無法應用在具有分階段特征的故障數據中，采用所提出的變點動態多階段可靠性評估模型分析了設備的可靠性。

圖1 某型微機控制輪對熒光磁粉探傷機故障數據變點估計

圖1b）展示了基于CUSUM 方法的可靠性變動過程的變點識別結果。圖1b）中，紅線代表了階段識別的結果，由此可知設備在經歷49 次故障后，設備的故障強度陡然降低，其可靠性水平大幅提升。經過現場調研和查閱檢修日志發現，從2017 年1 月1 日起經歷588 d 后設備經歷了一次大修，因此設備可靠性水平得到大幅度提升，這與CUSUM 算法分析結果相符合。

經過CUSUM 變點識別方法處理后，故障計數數據被分為2 個階段。所提出算法可自動地對2 個階段進行分別建模。圖2 展示了基于所提出模型對2 個階段進行分別建模后輸出的結果。圖2a）代表了對第1 階段故障數據建模的結果，圖2b）代表了對第2階段故障數據建模的結果。具體地，其中藍色實線代表了在不同時間上實際的故障累積數，而紅色的實線代表了所獲得的的非時齊泊松過程的均值函數。由圖2 可知，每一個階段的均值函數都與實際數據非常切合，這表明CUSUM 方法合理地將可靠性變動過程劃分為了2 個階段。

圖1、圖2 主要展示了對探傷設備進行可靠性評估的結果。而進一步地故障預測也是實際工程中所關注的一個重要問題。通常的故障預測結果通常以下面2 種形式所給出：①下次故障發生時間的預測；②給定區間內故障發生次數的預測。一旦給出故障時間和故障計數的預測，不僅可以從一個側面反映探傷設備當前可靠性水平，更重要的是可以據此進行維修資源、備份備件的安排和準備，以最終優化對設備的維修決策。為此，在圖3、圖4 中展示了基于所提出模型的故障預測結果。

圖2 基于所提出模型的故障數據建模

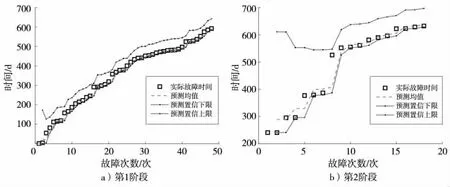
圖3 下一次故障發生時間的預測

圖4 未來200 d 內故障發生次數的預測

具體地，圖3 顯示了所提出方法分別在2 個階段對下一次故障發生時間的預測結果，其中正方形代表了實際故障時間，虛線代表了下次故障時間的預測均值，點劃線則代表了預測結果的99%置信上限與置信下限。由分析結果可知，所提出方法在兩個階段上所給出的99%置信區間能夠完全覆蓋實際故障的發生時間，其中第1 個階段置信區間較窄，第2 個階段置信區間較寬，這是由于故障發生次數較少所導致。此外，從圖中可以看出，下次故障發生時間的概率分布是一個長尾分布，因此有一定概率實際故障發生時間相對預測均值有比較大的正向偏離，這個結論從圖中的個別數據中也可觀察到。圖4 顯示未來200 d 內故障發生次數的預測，從圖中可以觀察到故障發生次數的概率分布相對對稱，90%置信上限與置信下限均勻分布于均值兩邊。同時可以觀察到在2 個階段中，所提出方法都較為準確的預測了200 d 內故障發生的累計次數。這表明所提出方法具有較好的故障預測性能，能為設備的運維計劃、備份備件計劃提供支持。

4 結語

鐵路車輛探傷設備的可靠性與人民的生命財產安全休戚相關，對其進行動態可靠性評估具有重要的價值。然而由于鐵路車輛探傷設備的定期進行大檢大修，車輛探傷設備的可靠性變動過程通常具有突變的特征，因此經典的AMSAA 模型難以實現對車輛探傷設備進行有效的評估。為此，本文融合了先進變點估計技術——CUSUM 方法與典型的非時齊Poisson 過程，提出了一種變點動態多階段可靠性評估模型。該模型一方面能夠通過對變點的切換來識別可靠性的突變，另一方面能夠通過對冪律參數b的調節來評估可靠性水平的變化，適用于鐵路車輛探傷設備可靠性評定的實際場景。采用所提出方法分析了西安鐵道車輛段某型微機控制輪對熒光磁粉探傷機故障時間數據，結果表明所提出方法能有效評估和預測鐵路探傷設備的可靠性。